В математике, особенно в числовой анализ, то Метод локальной линеаризации (LL) это общая стратегия проектирования числовые интеграторы для дифференциальных уравнений на основе локальной (кусочной) линеаризации данного уравнения на последовательных интервалах времени. Затем числовые интеграторы итеративно определяются как решение полученного кусочно-линейного уравнения в конце каждого последовательного интервала. Метод LL был разработан для множества уравнений, таких как обычный, отложенный, случайный и стохастический дифференциальные уравнения. Интеграторы LL являются ключевым компонентом в реализации методы вывода для оценки неизвестных параметров и ненаблюдаемых переменных дифференциальных уравнений, заданных Временные ряды (потенциально шумных) наблюдений. Схемы LL идеально подходят для работы со сложными моделями в различных областях, например нейробиология, финансы, управление лесным хозяйством, техника управления, математическая статистика, так далее.
Фон
Дифференциальные уравнения стали важным математическим инструментом для описания временной эволюции нескольких явлений, например вращения планет вокруг Солнца, динамики цен на активы на рынке, возгорания нейронов, распространения эпидемий и т. Д. поскольку точные решения этих уравнений обычно неизвестны, необходимы численные приближения к ним, полученные с помощью числовых интеграторов. В настоящее время многие приложения в инженерных и прикладных науках, сфокусированные на динамических исследованиях, требуют разработки эффективных числовых интеграторов, которые сохраняют, насколько это возможно, динамику этих уравнений. Исходя из этой основной мотивации, были разработаны интеграторы локальной линеаризации.
Метод локальной линеаризации высокого порядка
Метод локальной линеаризации высокого порядка (HOLL) является обобщением метода локальной линеаризации, ориентированным на получение интеграторов высокого порядка для дифференциальных уравнений, сохраняющих стабильность и динамика линейных уравнений. Интеграторы получаются путем разбиения на последовательные интервалы времени решения Икс исходного уравнения в двух частях: решение z локально линеаризованного уравнения плюс приближение высокого порядка невязки  .
.
Схема локальной линеаризации
А Схема локальной линеаризации (LL) это последний рекурсивный алгоритм что позволяет численно реализовать дискретизация полученный из метода LL или HOLL для класса дифференциальных уравнений.
LL методы для ODE
Рассмотрим d-размерный Обыкновенное дифференциальное уравнение (ODE)
![{ displaystyle { frac {d mathbf {x} left (t right)} {dt}} = mathbf {f} left (t, mathbf {x} left (t right) right) ), qquad t in left [t_ {0}, T right], qquad qquad qquad qquad (4.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b689077ae401751f25375eb3338ed66cc57f756a)
с начальным условием  , куда
, куда  - дифференцируемая функция.
- дифференцируемая функция.
Позволять  - дискретизация по времени временного интервала
- дискретизация по времени временного интервала ![{ displaystyle [t_ {0}, T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/986ba7ea2bc36ce31beb5c5f4faffbfb6405f69b) с максимальным шагом час такой, что
с максимальным шагом час такой, что  и
и  . После локальной линеаризации уравнения (4.1) на шаге по времени
. После локальной линеаризации уравнения (4.1) на шаге по времени  то вариация формулы констант дает
то вариация формулы констант дает

куда

получается из линейного приближения, и

- невязка линейного приближения. Здесь,  и
и  обозначим частные производные от ж по переменным Икс и тсоответственно и
обозначим частные производные от ж по переменным Икс и тсоответственно и  .
.
Локальная линейная дискретизация
Для дискретизации по времени  , то Локальная линейная дискретизация ОДУ (4.1) в каждой точке
, то Локальная линейная дискретизация ОДУ (4.1) в каждой точке  определяется рекурсивным выражением [1] [2]
определяется рекурсивным выражением [1] [2]

Локальная линейная дискретизация (4.3) сходится с заказом 2 к решению нелинейных ОДУ, но оно соответствует решению линейных ОДУ. Рекурсия (4.3) также известна как экспоненциальная дискретизация Эйлера.[3]
Локальные линейные дискретизации высокого порядка
Для дискретизации по времени  а Локальная линейная система высокого порядка (HOLL) дискретизация ОДУ (4.1) в каждой точке
а Локальная линейная система высокого порядка (HOLL) дискретизация ОДУ (4.1) в каждой точке  определяется рекурсивным выражением [1][4][5]
определяется рекурсивным выражением [1][4][5]

куда  это приказ
это приказ  (>2) приближение к невязке р
(>2) приближение к невязке р  Дискретизация ХОЛЛ (4.4) сходится с заказом
Дискретизация ХОЛЛ (4.4) сходится с заказом  к решению нелинейных ОДУ, но оно соответствует решению линейных ОДУ.
к решению нелинейных ОДУ, но оно соответствует решению линейных ОДУ.
Дискретизации HOLL можно получить двумя способами:[1][4][5][6] 1) (на основе квадратур) путем аппроксимации интегрального представления (4.2) р; и 2) (на основе интегратора) с использованием числового интегратора для дифференциального представления р определяется

для всех ![{ Displaystyle т ин lbrack t_ {k}, t_ {k + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dacd0fb31482f9ac95b8c3261d9dc00f1055dca4) , куда
, куда

Дискретизациями HOLL являются, например, следующие:
- Локально линеаризованная дискретизация Рунге-Кутты[6][4]

которое получается решением (4.5) через s-этапный явный Схема Рунге – Кутта (РК) с коэффициентами ![{ displaystyle mathbf {c} = left [c_ {i} right], mathbf {A} = left [a_ {ij} right] quad и quad mathbf {b} = left [ b_ {j} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fbc317004aaf306e62ecc1c6d08e4f49d9d0543) .
.
- Локальная линейная дискретизация Тейлора[5]

что является результатом приближения  в (4.2) по порядкуп усеченный Расширение Тейлора.
в (4.2) по порядкуп усеченный Расширение Тейлора.
- Многоступенчатая дискретизация экспоненциального распространения

который является результатом интерполяции  в (4.2) полиномом степени п на
в (4.2) полиномом степени п на  , куда
, куда  обозначает j-го обратная разница из
обозначает j-го обратная разница из  .
.
- Дискретизация экспоненциального распространения типа Рунге-Кутты [7]

который является результатом интерполяции  в (4.2) полиномом степени п на
в (4.2) полиномом степени п на  ,
,
- Линеализованная экспоненциальная дискретизация Адамса[8]

который является результатом интерполяции  в (4.2) на Многочлен Эрмита степени п на
в (4.2) на Многочлен Эрмита степени п на  .
.
Схемы локальной линеаризации
Вся численная реализация  дискретизации LL (или HOLL)
дискретизации LL (или HOLL)  включает приближения
включает приближения  к интегралам
к интегралам  формы
формы

куда А это d  d матрица. Каждая численная реализация
d матрица. Каждая численная реализация  LL (или HOLL)
LL (или HOLL)  любого порядка обычно называется Схема локальной линеаризации.[1][9]
любого порядка обычно называется Схема локальной линеаризации.[1][9]
Вычисление интегралов с матричной экспонентой
Среди ряда алгоритмов вычисления интегралов  предпочтение отдается приближениям рациональных подпространств Паде и Крылова для экспоненциальной матрицы. Центральную роль в этом играет выражение[10][5][11]
предпочтение отдается приближениям рациональных подпространств Паде и Крылова для экспоненциальной матрицы. Центральную роль в этом играет выражение[10][5][11]

куда  находятся d-мерные векторы,
находятся d-мерные векторы,

![{ displaystyle mathbf {L} = [ mathbf {I} quad mathbf {0} _ {d times l}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75b8ac2636b6ebd86e0bba8f06886336cfc6ec82) ,
, ![{ displaystyle mathbf {r} = [ mathbf {0} _ {1 times (d + l-1)} quad 1] ^ { intercal}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e4832a55ccffda573260201924fed69152a784) ,
,  , существование
, существование  то d-мерная единичная матрица.
то d-мерная единичная матрица.
Если  обозначает (р; д) -Приближение Паде из
обозначает (р; д) -Приближение Паде из  и k наименьшее натуральное число такое, что
и k наименьшее натуральное число такое, что  [12][9]
[12][9]

Если  обозначает (м; р; д; к) Приближение Крылова-Паде из
обозначает (м; р; д; к) Приближение Крылова-Паде из  , тогда [12]
, тогда [12]

куда  - размерность подпространства Крылова.
- размерность подпространства Крылова.
Заказать 2 схемы ЛЛ
 [13][9]
[13][9] 
где матрицы  , L и р определены как
, L и р определены как

![{ displaystyle mathbf {L} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 2} end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05d54f18477ecdb4b717abf25a75b96d17729bcd) и
и ![{ displaystyle mathbf {r} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 1)} & 1 end {array}} верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f82230fb66e66705351377690e9f14c8d4a41224) с
с  . Для больших систем ODE [3]
. Для больших систем ODE [3]

Заказать 3 схемы ЛЛ-Тейлора
 [5]
[5] 
где для автономный ОДУ матрицы  и
и  определены как
определены как
![{ displaystyle mathbf {T} _ {n} = left [{ begin {array} {cccc} mathbf {f} _ { mathbf {x}} ( mathbf {y} _ {n}) & ( mathbf {I} otimes mathbf {f} ^ { intercal} ( mathbf {y} _ {n})) mathbf {f} _ { mathbf {xx}} ( mathbf {y} _ {n}) mathbf {f} ( mathbf {y} _ {n}) & mathbf {0} & mathbf {f} ( mathbf {y} _ {n}) 0 & 0 & 0 & 0 0 & 0 & 0 & 1 0 & 0 & 0 & 0 end {array}} right] in mathbb {R} ^ {(d + 3) times (d + 3)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b4535597fcece8be4c40e7b4ae75229d8f9831)
![{ displaystyle mathbf {L} _ {1} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 3} end {array}} right] quad и quad mathbf {r} _ {1} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 2)} & 1 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f495cb0102ab17316c499936bd236cdb35f4ebbd) . Здесь,
. Здесь,  обозначает вторую производную от ж относительно Икс, и р + д> 2. Для больших систем ODE
обозначает вторую производную от ж относительно Икс, и р + д> 2. Для больших систем ODE

Заказать 4 схемы ЛЛ-РК
 [4] [6]
[4] [6] 
куда

и

с ![{ displaystyle mathbf {k} _ {1} Equiv mathbf {0}, c = left [{ begin {array} {cccc} 0 & { frac {1} {2}} & { frac { 1} {2}} & 1 end {array}} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7569810b131c3d8e9ad24b6201f9454d90fbbc) и р + д> 3. Для больших систем ОДУ вектор
и р + д> 3. Для больших систем ОДУ вектор  в приведенной выше схеме заменен на
в приведенной выше схеме заменен на  с
с 
Локально линеаризованная схема Рунге-Кутты Дорманда и Принца
 [14] [15]
[14] [15]
куда s = 7 это количество ступеней,

с  , и
, и  являются Коэффициенты Рунге-Кутты Дорманда и Принца и р + д> 4. Вектор
являются Коэффициенты Рунге-Кутты Дорманда и Принца и р + д> 4. Вектор  в приведенной выше схеме вычисляется с помощью приближения Паде или Крилора-Паде для малых или больших систем ОДУ соответственно.
в приведенной выше схеме вычисляется с помощью приближения Паде или Крилора-Паде для малых или больших систем ОДУ соответственно.
Стабильность и динамика
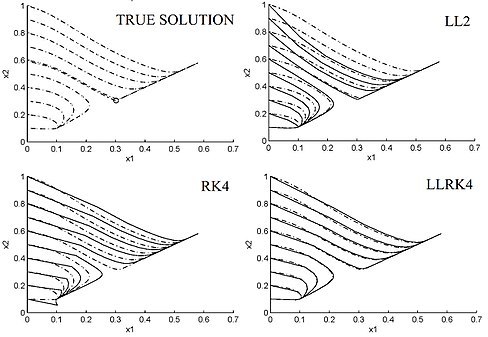
рисунок 1 Фазовый портрет (пунктирная линия) и приближенный фазовый портрет (сплошная линия) нелинейного ОДУ (4.10) - (4.11), вычисленных по схеме LL второго порядка (4.2), классической схеме Ругена-Кутты четвертого порядка
РК4,
и порядка 4 ЛЛРК4 схемы (4.8) с шагом h = 1/2, p = q = 6.
По построению дискретизации LL и HOLL наследуют устойчивость и динамику линейных ОДУ, но это не относится к схемам LL в целом. С  , схемы ЛЛ (4.6) - (4.9) имеют вид А-стабильный.[4] С q = p + 1 или q = p + 2, схемы ЛЛ (4.6) - (4.9) также являются L-стабильный.[4] Для линейных ОДУ схемы ЛЛ (4.6) - (4.9) сходятся с порядком р + д [4] [9]. Кроме того, с р = д = 6 и
, схемы ЛЛ (4.6) - (4.9) имеют вид А-стабильный.[4] С q = p + 1 или q = p + 2, схемы ЛЛ (4.6) - (4.9) также являются L-стабильный.[4] Для линейных ОДУ схемы ЛЛ (4.6) - (4.9) сходятся с порядком р + д [4] [9]. Кроме того, с р = д = 6 и  = d, все описанные выше схемы LL поддаются «точному вычислению» (с точностью до арифметика с плавающей запятой ) линейных ОДУ на современных персональных компьютерах [4] [9]. Это включает в себя жесткий и сильно колеблющиеся линейные уравнения. Более того, схемы ЛЛ (4.6) - (4.9) регулярны для линейных ОДУ и наследуют симплектическая структура из Гамильтониан гармонические осцилляторы.[5][13] Эти схемы LL также сохраняют линеаризацию и лучше воспроизводят устойчивые и неустойчивые многообразия вокруг точки гиперболического равновесия и периодические орбиты который другие числовые схемы с таким же размером [9].[5][13] Например, на рисунке 1 показан фазовый портрет ODE
= d, все описанные выше схемы LL поддаются «точному вычислению» (с точностью до арифметика с плавающей запятой ) линейных ОДУ на современных персональных компьютерах [4] [9]. Это включает в себя жесткий и сильно колеблющиеся линейные уравнения. Более того, схемы ЛЛ (4.6) - (4.9) регулярны для линейных ОДУ и наследуют симплектическая структура из Гамильтониан гармонические осцилляторы.[5][13] Эти схемы LL также сохраняют линеаризацию и лучше воспроизводят устойчивые и неустойчивые многообразия вокруг точки гиперболического равновесия и периодические орбиты который другие числовые схемы с таким же размером [9].[5][13] Например, на рисунке 1 показан фазовый портрет ODE


с  ,
,  и
и  , и его аппроксимация различными схемами. Эта система имеет два устойчивые стационарные точки и один неустойчивая стационарная точка в регионе
, и его аппроксимация различными схемами. Эта система имеет два устойчивые стационарные точки и один неустойчивая стационарная точка в регионе  .
.
LL методы для DDE
Рассмотрим d-размерный Дифференциальное уравнение задержки (DDE)
![{ displaystyle { frac {d mathbf {x} left (t right)} {dt}} = mathbf {f} left (t, mathbf {x} left (t right), mathbf {x} _ {t} (- tau _ {1}), cdots, mathbf {x} _ {t} (- tau _ {m}) right), qquad t in left [t_ {0}, T right], qquad qquad (5.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/697d2b4993df9f04063023258c020c16b2472d0b)
с м постоянные задержки  и начальное состояние
и начальное состояние  для всех
для всех ![{ Displaystyle s in left [- tau, 0 right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36e0323b0f49a9ff410710f3d23bece839ede3f2) куда ж - дифференцируемая функция,
куда ж - дифференцируемая функция, ![{ displaystyle mathbf {x} _ {t}: left [- tau, 0 right] longrightarrow mathbb {R} ^ {d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9da7f52b7080c8d8314732acbf3869a6a690a0a6) сегментная функция, определяемая как
сегментная функция, определяемая как
![{ displaystyle mathbf {x} _ {t} (s): = mathbf {x} (t + s), { text {}} s in left [- tau, 0 right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57496edc39f42753319edb6dbf8096b2d828dc67)
для всех ![{ displaystyle t in left [t_ {0}, T right], mathbf { varphi}: left [- tau, 0 right] longrightarrow mathbb {R} ^ {d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09acb929ae865c8b9aa16afe15c70e21c14caba2) - заданная функция, а
- заданная функция, а 
Локальная линейная дискретизация
Для дискретизации по времени  , то Локальная линейная дискретизация ДДУ (5.1) в каждой точке
, то Локальная линейная дискретизация ДДУ (5.1) в каждой точке  определяется рекурсивным выражением [11]
определяется рекурсивным выражением [11]

куда
![{ displaystyle Phi (t_ {n}, mathbf {z} _ {n}, h_ {n}; { widetilde { mathbf {z}}} _ {t_ {n}} ^ {1} ,. ., { widetilde { mathbf {z}}} _ {t_ {n}} ^ {m}) = int limits _ {0} ^ {h_ {n}} e ^ { mathbf {A} _ {n} (h_ {n} -u)} [ sum limits _ {i = 1} ^ {m} mathbf {B} _ {n} ^ {i} ({ widetilde { mathbf {z} }} _ {t_ {n}} ^ {i} left (u- tau _ {i} right) - { widetilde { mathbf {z}}} _ {t_ {n}} ^ {i} left (- tau _ {i} right)) + mathbf {d} _ {n}] du + int limits _ {0} ^ {h_ {n}} int limits _ {0} ^ {u} e ^ { mathbf {A} _ {n} (h_ {n} -u)} mathbf {c} _ {n} drdu}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8033183d307bbeb3a581e56e311a6e526af0fff1)
![{ displaystyle { widetilde { mathbf {z}}} _ {t_ {n}} ^ {i}: left [- tau _ {i}, 0 right] longrightarrow mathbb {R} ^ { d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3f4bc0cc5b10a10d0844d2265aababd5028d6e4) сегментная функция, определяемая как
сегментная функция, определяемая как
![{ displaystyle { widetilde { mathbf {z}}} _ {t_ {n}} ^ {i} (s): = { widetilde { mathbf {z}}} ^ {i} (t_ {n} + s), { text {}} s in left [- tau _ {i}, 0 right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6d1f224746bba85bb53d4f2acd5b76b1f50eeef)
и ![{ displaystyle { widetilde { mathbf {z}}} ^ {i}: left [t_ {n} - tau _ {i}, t_ {n} right] longrightarrow mathbb {R} ^ { d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922ac10d7369b3ff0ffe9487ebb8a509a1305574) является подходящим приближением к
является подходящим приближением к  для всех
для всех ![{ displaystyle t in lbrack t_ {n} - tau _ {i}, t_ {n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f287009ce5d61c9d7ed2a843c93dfdef6226a50) такой, что
такой, что  Здесь,
Здесь,

- постоянные матрицы и

- постоянные векторы.  обозначим соответственно частные производные от ж по переменным т и Икс, и
обозначим соответственно частные производные от ж по переменным т и Икс, и  . Локально-линейная дискретизация (5.2) сходится к решению (5.1) с порядком
. Локально-линейная дискретизация (5.2) сходится к решению (5.1) с порядком  если
если  приблизительно
приблизительно  с заказом
с заказом  для всех
для всех ![{ Displaystyle и в lbrack 0, h_ {n}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/956d5d79b8e61251940a26652b1ecead7daa8b6c) .
.
Схемы локальной линеаризации

Рис. 2 Примерные пути
Марчук и др. (1991) противовирусная иммунная модель, описываемая жесткой системой десятимерных нелинейных DDE с пятью временными задержками: вверху,
сплошная Рунге-Кутта (2,3) схема ; botom, схема LL (5.3). Размер шага
в = 0,01 фиксированный, и
р = д = 6.
В зависимости от приближений  и алгоритма вычисления
и алгоритма вычисления  могут быть определены различные схемы локальной линеаризации. Каждая числовая реализация
могут быть определены различные схемы локальной линеаризации. Каждая числовая реализация  локальной линейной дискретизации
локальной линейной дискретизации  обычно называется Схема локальной линеаризации.
обычно называется Схема локальной линеаризации.
Полиномиальные схемы LL порядка 2
 [11]
[11] 
где матрицы  и
и  определены как
определены как

![{ displaystyle mathbf {L} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 2} end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05d54f18477ecdb4b717abf25a75b96d17729bcd) и
и ![{ displaystyle mathbf {r} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 1)} & 1 end {array}} справа], h_ {n} leq tau}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05fdb2050667c7b12025db96c59b015211204a57) , и
, и  . Здесь матрицы
. Здесь матрицы  ,
,  ,
,  и
и  определены как в (5.2), но с заменой
определены как в (5.2), но с заменой  к
к  и
и  куда
куда

с  , это Локальная линейная аппроксимация к решению (5.1), определенному по схеме ЛЛ (5.3) для всех
, это Локальная линейная аппроксимация к решению (5.1), определенному по схеме ЛЛ (5.3) для всех ![{ displaystyle t in lbrack t_ {0}, t_ {n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed17e1a454d79e9e85aa3fdb316727d17eb069b) и по
и по  за
за ![{ displaystyle t in left [t_ {0} - tau, t_ {0} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99fafe4165d02d310ce7c3f55c6fbfc1742d2d65) . Для больших систем DDE
. Для больших систем DDE

с  и
и  . Рис. 2 иллюстрирует устойчивость схемы LL (5.3) и явной схемы аналогичного порядка во включении жестких систем DDE.
. Рис. 2 иллюстрирует устойчивость схемы LL (5.3) и явной схемы аналогичного порядка во включении жестких систем DDE.
Методы LL для RDE
Рассмотрим d-размерное случайное дифференциальное уравнение (RDE)
![{ displaystyle { frac {d mathbf {x} left (t right)} {dt}} = mathbf {f} ( mathbf {x} (t), mathbf { xi} (t) ), quad t in left [t_ {0}, T right], qquad qquad qquad (6.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e7f4c5cbe530e829f8edf84e2e49d0829a2ef0)
с начальным условием  куда
куда  это k-размерный сепарабельный конечный непрерывный случайный процесс, и ж - дифференцируемая функция. Предположим, что реализация (путь) из
это k-размерный сепарабельный конечный непрерывный случайный процесс, и ж - дифференцируемая функция. Предположим, что реализация (путь) из  дано.
дано.
Локальная линейная дискретизация
Для дискретизации по времени  , то Локальная линейная дискретизация ВДЭ (6.1) в каждой точке
, то Локальная линейная дискретизация ВДЭ (6.1) в каждой точке  определяется рекурсивным выражением [16]
определяется рекурсивным выражением [16]

куда

и  приближение к процессу
приближение к процессу  для всех
для всех ![{ displaystyle t in left [t_ {0}, T right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aedde214e225a352a24c1c922043d56a7d90588b) Здесь,
Здесь,  и
и  обозначим частные производные от
обозначим частные производные от  относительно
относительно  и
и  , соответственно.
, соответственно.
Схемы локальной линеаризации

Рис. 3 Фазовый портрет траекторий движения Эйлер и LL схемы интегрирования нелинейного ВДУ (6.2) - (6.3) с шагом в = 1/32, и р = д = 6.
В зависимости от приближений  к процессу
к процессу  и алгоритма вычисления
и алгоритма вычисления  могут быть определены различные схемы локальной линеаризации. Каждая численная реализация
могут быть определены различные схемы локальной линеаризации. Каждая численная реализация  локальной линейной дискретизации
локальной линейной дискретизации  обычно называется Схема локальной линеаризации.
обычно называется Схема локальной линеаризации.
Схемы LL
 [16] [17]
[16] [17]где матрицы  определены как
определены как
![{ displaystyle mathbf {M} _ {n} = left [{ begin {array} {ccc} mathbf {f} _ { mathbf {x}} left ( mathbf {y} _ {n} , mathbf { xi} (t_ {n}) right) & mathbf {f} _ { mathbf { xi}} ( mathbf {y} _ {n}, mathbf { xi} (t_ {n}) ( mathbf { xi} (t_ {n + 1}) - mathbf { xi} (t_ {n})) / h_ {n} & mathbf {f} left ( mathbf { y} _ {n}, mathbf { xi} (t_ {n}) right) 0 & 0 & 1 0 & 0 & 0 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de2e549c00febeadc80e1df68d44a6a66abd159a)
![{ displaystyle mathbf {L} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 2} end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05d54f18477ecdb4b717abf25a75b96d17729bcd) ,
, ![{ displaystyle mathbf {r} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 1)} & 1 end {array}} верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f82230fb66e66705351377690e9f14c8d4a41224) , и р + д> 1. Для больших систем RDE[17]
, и р + д> 1. Для больших систем RDE[17]

Скорость сходимости обеих схем равна  , где
, где  экспонента условия Гельдера
экспонента условия Гельдера  .
.
На рис.3 представлен фазовый портрет ВДЭ.


и его аппроксимация двумя численными схемами, где  обозначает дробный броуновский процесс с Показатель Херста H = 0,45.
обозначает дробный броуновский процесс с Показатель Херста H = 0,45.
Сильные методы LL для SDE
Рассмотрим d-размерный Стохастическое дифференциальное уравнение (SDE)
![{ displaystyle d mathbf {x} (t) = mathbf {f} (t, mathbf {x} (t)) dt + sum limits _ {i = 1} ^ {m} mathbf {g} _ {i} (t) d mathbf {w} ^ {i} (t), quad t in left [t_ {0}, T right], qquad qquad qquad (7.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/464be59af5611f27dd6d946030a7202ce481c427)
с начальным условием  , где коэффициент сноса
, где коэффициент сноса  а коэффициент диффузии
а коэффициент диффузии  - дифференцируемые функции, а
- дифференцируемые функции, а  является м-размерный стандарт Винеровский процесс.
является м-размерный стандарт Винеровский процесс.
Локальная линейная дискретизация
Для дискретизации по времени  , приказ-
, приказ- (=1,1.5) Сильная локальная линейная дискретизация решения СДУ (7.1) определяется рекурсивным соотношением [18] [19]
(=1,1.5) Сильная локальная линейная дискретизация решения СДУ (7.1) определяется рекурсивным соотношением [18] [19]

куда

и

Здесь,

 обозначим частные производные от
обозначим частные производные от  with respect to the variables
with respect to the variables  и тсоответственно и
и тсоответственно и  the Hessian matrix of
the Hessian matrix of  относительно
относительно  . The strong Local Linear discretization
. The strong Local Linear discretization  сходится с заказом
сходится с заказом  (=1,1.5) to the solution of (7.1).
(=1,1.5) to the solution of (7.1).
High Order Local Linear discretizations
After the local linearization of the drift term of (7.1) at  , the equation for the residual
, the equation for the residual  дан кем-то
дан кем-то

для всех ![{ Displaystyle т ин lbrack t_ {n}, t_ {n + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b15f801777044ac19f6f4e6551c3e78da54f33c5) , куда
, куда

А High Order Local Linear discretization of the SDE (7.1) at each point  is then defined by the recursive expression [20]
is then defined by the recursive expression [20]

куда  is a strong approximation to the residual
is a strong approximation to the residual  порядка
порядка  выше чем 1.5. The strong HOLL discretization
выше чем 1.5. The strong HOLL discretization  converges with order
converges with order  to the solution of (7.1).
to the solution of (7.1).
Local Linearization schemes
Depending on the way of computing  ,
,  и
и  different numerical schemes can be obtained. Every numerical implementation
different numerical schemes can be obtained. Every numerical implementation  of a strong Local Linear discretization
of a strong Local Linear discretization  of any order is generically called Strong Local Linearization (SLL) scheme.
of any order is generically called Strong Local Linearization (SLL) scheme.
Order 1 SLL schemes
 [21]
[21] 
где матрицы  ,
,  и
и  are defined as in (4.6),
are defined as in (4.6),  является i.i.d. zero mean Gaussian random variable с отклонением
является i.i.d. zero mean Gaussian random variable с отклонением  , и p+q>1. For large systems of SDEs,[21] in the above scheme
, и p+q>1. For large systems of SDEs,[21] in the above scheme  заменяется на
заменяется на  .
.
Order 1.5 SLL schemes

где матрицы  ,
,  и
и  определены как
определены как

![{ displaystyle mathbf {L} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 2} end {array}} right], mathbf {r} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 1)} & 1 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4096111183a23671fc2d181a96e16ca7b7df6d6c) ,
,  is a i.i.d. zero mean Gaussian random variable with variance
is a i.i.d. zero mean Gaussian random variable with variance  and covariance
and covariance  и p+q>1 [12]. For large systems of SDEs,[12] in the above scheme
и p+q>1 [12]. For large systems of SDEs,[12] in the above scheme  заменяется на
заменяется на  .
.
Order 2 SLL-Taylor schemes


куда  ,
,  ,
,  и
и  are defined as in the order-1 SLL schemes, and
are defined as in the order-1 SLL schemes, and  is order 2 approximation to the multiple Stratonovish integral
is order 2 approximation to the multiple Stratonovish integral  .[20]
.[20]
Order 2 SLL-RK schemes

Fig. 4, Top: Evolution of domains in the phase plane of the harmonic oscillator (7.6), with ε=0 and ω=σ=1. Images of the initial unit circle (green) are obtained at three time moments
Т by the exact solution (black), and by the schemes
SLL1 (синий) и
Implicit Euler (red) with
h=0.05.
Нижний: Expected value of the energy (solid line) along the solution of the nonlinear oscillator (7.6), with ε=1 and ω=100, and its approximation (circles) computed via
Монте-Карло с
10000 моделирование
SLL1 схема с
h=1/2 и
p=q=6.
For SDEs with a single Wiener noise (m=1) [20]


куда






с  .
.
Здесь,  для низкоразмерных SDE, и
для низкоразмерных SDE, и  для крупных систем ДЗО, где
для крупных систем ДЗО, где  ,
,  ,
,  ,
,  и
и  определяются как в следующем порядке:2 Схемы SLL-Тейлора, р + д> 1 и
определяются как в следующем порядке:2 Схемы SLL-Тейлора, р + д> 1 и  .
.
Стабильность и динамика
По построению сильные дискретизации LL и HOLL наследуют устойчивость и динамика линейных СДУ, но это не случай сильных схем LL в целом. Схемы ЛЛ (7.2) - (7.5) с  находятся А-устойчивые, включая жесткие и сильно колеблющиеся линейные уравнения.[12] Причем для линейных СДУ с случайные аттракторы, эти схемы также имеют случайный аттрактор, который сходится по вероятности к точному при уменьшении шага и сохранении эргодичность этих уравнений для любого шага.[20][12] Эти схемы также воспроизводят важные динамические свойства простых и связанных гармонических осцилляторов, такие как линейный рост энергии вдоль путей, колебательное поведение около 0, симплектическая структура гамильтоновых осцилляторов и среднее значение путей.[20][22] Для нелинейных СДУ с малым шумом (т. Е. (7.1) с
находятся А-устойчивые, включая жесткие и сильно колеблющиеся линейные уравнения.[12] Причем для линейных СДУ с случайные аттракторы, эти схемы также имеют случайный аттрактор, который сходится по вероятности к точному при уменьшении шага и сохранении эргодичность этих уравнений для любого шага.[20][12] Эти схемы также воспроизводят важные динамические свойства простых и связанных гармонических осцилляторов, такие как линейный рост энергии вдоль путей, колебательное поведение около 0, симплектическая структура гамильтоновых осцилляторов и среднее значение путей.[20][22] Для нелинейных СДУ с малым шумом (т. Е. (7.1) с  ), пути этих схем SLL в основном являются неслучайными путями схемы LL (4.6) для ODE плюс небольшое возмущение, связанное с небольшим шумом. В этой ситуации динамические свойства этой детерминированной схемы, такие как сохранение линеаризации и сохранение точной динамики решения вокруг точек гиперболического равновесия и периодических орбит, становятся актуальными для путей схемы SLL.[20] Например, на рис. 4 показаны эволюция доменов на фазовой плоскости и энергия стохастического осциллятора.
), пути этих схем SLL в основном являются неслучайными путями схемы LL (4.6) для ODE плюс небольшое возмущение, связанное с небольшим шумом. В этой ситуации динамические свойства этой детерминированной схемы, такие как сохранение линеаризации и сохранение точной динамики решения вокруг точек гиперболического равновесия и периодических орбит, становятся актуальными для путей схемы SLL.[20] Например, на рис. 4 показаны эволюция доменов на фазовой плоскости и энергия стохастического осциллятора.

и их аппроксимации двумя численными схемами.
Слабые методы LL для SDE
Рассмотрим d-мерное стохастическое дифференциальное уравнение
![{ displaystyle d mathbf {x} (t) = mathbf {f} (t, mathbf {x} (t)) dt + sum limits _ {i = 1} ^ {m} mathbf {g} _ {i} (t) d mathbf {w} ^ {i} (t), qquad t in left [t_ {0}, T right], qquad qquad (8.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4db0bd45e90a7c91e2715a14caf58e220b2e0b36)
с начальным условием  , где коэффициент сноса
, где коэффициент сноса  а коэффициент диффузии
а коэффициент диффузии  - дифференцируемые функции, а
- дифференцируемые функции, а  является м-мерный стандартный винеровский процесс.
является м-мерный стандартный винеровский процесс.
Локальная линейная дискретизация
Для дискретизации по времени  , приказ-
, приказ-
 Слабая локальная линейная дискретизация решения СДУ (8.1) определяется рекурсивным соотношением [23]
Слабая локальная линейная дискретизация решения СДУ (8.1) определяется рекурсивным соотношением [23]

куда

с

и  представляет собой случайный процесс с нулевым средним с матрицей дисперсии
представляет собой случайный процесс с нулевым средним с матрицей дисперсии

Здесь,  ,
,  обозначим частные производные от
обозначим частные производные от  по переменным
по переменным  и т, соответственно,
и т, соответственно,  матрица Гессе
матрица Гессе  относительно
относительно  , и
, и ![{ displaystyle mathbf {G} (t) = [ mathbf {g} _ {1} (t), ..., mathbf {g} _ {m} (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9198e9be76ab6056339bf885c5835f38b50399e4) . Слабая локальная линейная дискретизация
. Слабая локальная линейная дискретизация  сходится с заказом
сходится с заказом  (= 1,2) к решению (8.1).
(= 1,2) к решению (8.1).
Схемы локальной линеаризации
В зависимости от способа вычисления  и
и  могут быть получены различные численные схемы. Каждая численная реализация
могут быть получены различные численные схемы. Каждая численная реализация  слабой локальной линейной дискретизации
слабой локальной линейной дискретизации  обычно называется Схема слабой локальной линеаризации (WLL).
обычно называется Схема слабой локальной линеаризации (WLL).
Схема заказа 1 WLL
 [24] [25]
[24] [25]
где для СДУ с автономными коэффициентами диффузии  ,
,  и
и  - подматрицы, определяемые разделенная матрица
- подматрицы, определяемые разделенная матрица  , с
, с
![{ displaystyle { mathcal {M}} _ {n} = left [{ begin {array} {cccc} mathbf {f} _ { mathbf {x}} (t_ {n}, mathbf {y } _ {n}) & mathbf {GG} ^ { intercal} & mathbf {f} _ {t} (t_ {n}, mathbf {y} _ {n}) & mathbf {f} ( t_ {n}, mathbf {y} _ {n}) mathbf {0} & - mathbf {f} _ { mathbf {x}} ^ { intercal} (t_ {n}, mathbf {y} _ {n}) & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & 0 & 1 mathbf {0} & mathbf {0} & 0 & 0 end {массив}} right] in mathbb {R} ^ {(2d + 2) times (2d + 2)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b6c5cb6cc2c1a036002082a4dcad32b5080660)
и  это последовательность d-размерный независимый двухточечные распределенные случайные векторы удовлетворение
это последовательность d-размерный независимый двухточечные распределенные случайные векторы удовлетворение  .
.
Схема WLL порядка 2
 [24] [25]
[24] [25]
куда  ,
,  и
и  - подматрицы, определяемые разделенной матрицей
- подматрицы, определяемые разделенной матрицей  с
с
![{ displaystyle { mathcal {M}} _ {n} = left [{ begin {array} {cccccc} mathbf {J} & mathbf {H} _ {2} & mathbf {H} _ { 1} & mathbf {H} _ {0} & mathbf {a} _ {2} & mathbf {a} _ {1} mathbf {0} & - mathbf {J} ^ { intercal } & mathbf {I} & mathbf {0} & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & - mathbf {J} ^ { intercal} & mathbf {I} & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & mathbf {0} & - mathbf {J} ^ { intercal} & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & mathbf {0} & mathbf {0} & 0 & 1 mathbf {0} & mathbf {0} & mathbf {0} & mathbf {0} & 0 & 0 end {array}} right] in mathbb {R} ^ {(4d + 2) times (4d + 2)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92d5869bcb0a0b5db4944c8170713c0c5a096a6)

и

Стабильность и динамика

Рис. 5 Приближенное среднее SDE (8.2), вычисленное методом Монте-Карло с 100 моделирование различных схем с в = 1/16 и р = д = 6.
По построению слабые LL-дискретизации наследуют устойчивость и динамика линейных СДУ, но это не относится к слабым схемам LL в целом. Схемы WLL, с  сохранить первые два момента линейных СДУ и наследует среднеквадратичную устойчивость или нестабильность, которые может иметь такое решение.[24] Это включает, например, уравнения связанных гармонических осцилляторов, управляемых случайной силой, и большие системы жестких линейных СДУ, которые являются результатом метода линий для линейных стохастических уравнений в частных производных. Более того, эти схемы WLL сохраняют эргодичность линейных уравнений, и геометрически эргодичны для некоторых классов нелинейных СДУ.[26] Для нелинейных СДУ с малым шумом (т.е. (8.1) с
сохранить первые два момента линейных СДУ и наследует среднеквадратичную устойчивость или нестабильность, которые может иметь такое решение.[24] Это включает, например, уравнения связанных гармонических осцилляторов, управляемых случайной силой, и большие системы жестких линейных СДУ, которые являются результатом метода линий для линейных стохастических уравнений в частных производных. Более того, эти схемы WLL сохраняют эргодичность линейных уравнений, и геометрически эргодичны для некоторых классов нелинейных СДУ.[26] Для нелинейных СДУ с малым шумом (т.е. (8.1) с  ), решения этих схем WLL в основном представляют собой неслучайные пути схемы LL (4.6) для ОДУ плюс небольшое возмущение, связанное с малым шумом. В этой ситуации динамические свойства этой детерминированной схемы, такие как сохранение линеаризации и сохранение точной динамики решения вокруг точек гиперболического равновесия и периодических орбит, становятся актуальными для среднего значения схемы WLL.[24] Например, на рис. 5 показано приблизительное среднее значение SDE
), решения этих схем WLL в основном представляют собой неслучайные пути схемы LL (4.6) для ОДУ плюс небольшое возмущение, связанное с малым шумом. В этой ситуации динамические свойства этой детерминированной схемы, такие как сохранение линеаризации и сохранение точной динамики решения вокруг точек гиперболического равновесия и периодических орбит, становятся актуальными для среднего значения схемы WLL.[24] Например, на рис. 5 показано приблизительное среднее значение SDE

вычисляется по различным схемам.
Исторические заметки
Ниже представлена временная шкала основных разработок метода локальной линеаризации (LL).
- Папа Д.А. (1963) вводит LL-дискретизацию для ODE и схему LL, основанную на разложении Тейлора. [2]
- Одзаки Т. (1985) вводит метод LL для интеграции и оценки SDE. Термин «локальная линеаризация» используется впервые. [27]
- Biscay R. et al. (1996) переформулировали сильный метод LL для SDE.[19]
- Сёдзи И. и Одзаки Т. (1997) переформулируют метод слабого LL для SDE.[23]
- Hochbruck M. et al. (1998) вводят схему ЛЛ для ОДУ, основанную на аппроксимации подпространства Крылова. [3]
- Jimenez J.C. (2002) вводит схему LL для ОДУ и СДУ, основанную на рациональной аппроксимации Паде. [21]
- Карбонелл Ф. и другие. (2005) представили метод LL для RDE. [16]
- Jimenez J.C. et al. (2006) представили метод LL для DDE. [11]
- Де ла Круз Х. и др. (2006, 2007) и Tokman M. (2006) представляют два класса интеграторов HOLL для ODE: основанные на интеграторах [6] и квадратурные.[7][5]
- Де ла Круз Х. и др. (2010) представили сильный метод HOLL для SDE. [20]
Рекомендации
- ^ а б c d Хименес Дж. К. (2009). «Методы локальной линеаризации для численного интегрирования обыкновенных дифференциальных уравнений: обзор». Технический отчет ICTP. 035: 357–373.
- ^ а б Поуп, Д. А. (1963). «Экспоненциальный метод численного интегрирования обыкновенных дифференциальных уравнений». Comm. АКМ, 6 (8), 491-493. DOI: 10.1145 / 366707.367592
- ^ а б c Хохбрук М., Любич К. и Зельхофер Х. (1998). «Экспоненциальные интеграторы для больших систем дифференциальных уравнений». SIAM J. Scient. Comput. 19 (5), 1552–1574.DOI: 10.1137 / S1064827595295337
- ^ а б c d е ж грамм час de la Cruz H .; Biscay R.J .; Jimenez J.C .; Карбонелл Ф. (2013). «Локальная линеаризация - методы Рунге-Кутты: класс A-устойчивых явных интеграторов для динамических систем». Математика. Comput. Моделирование. 57 (3–4): 720–740. DOI: 10.1016 / j.mcm.2012.08.011.
- ^ а б c d е ж грамм час de la Cruz H .; Biscay R.J .; Carbonell F .; Ozaki T .; Хименес Дж. К. (2007). «Метод локальной линеаризации высшего порядка для решения обыкновенных дифференциальных уравнений». Appl. Математика. Comput. 185: 197–212. DOI: 10.1016 / j.amc.2006.06.096.
- ^ а б c d de la Cruz H .; Biscay R.J .; Carbonell F .; Jimenez J.C .; Одзаки Т. (2006). «Методы локальной линеаризации-Рунге-Кутты (LLRK) для решения обыкновенных дифференциальных уравнений». Лекция по информатике 3991: 132–139, Springer-Verlag. DOI: 10.1007 / 11758501_22. ISBN 978-3-540-34379-0.
- ^ а б Токман М. (2006). «Эффективная интеграция больших жестких систем ODE с итеративными методами экспоненциального распространения (EPI)». J. Comput. Физика. 213 (2): 748–776.DOI: 10.1016 / j.jcp.2005.08.032.
- ^ М. Хохбрук .; А. Остерманн. (2011). «Экспоненциальные многошаговые методы типа Адамса». BIT Numer. Математика. 51 (4): 889–908. DOI: 10.1007 / s10543-011-0332-6.
- ^ а б c d е ж Хименес, Дж. К., и Карбонелл, Ф. (2005). «Скорость сходимости схем локальной линеаризации начальных задач». Appl. Математика. Вычисл., 171 (2), 1282-1295. DOI: 10.1016 / j.amc.2005.01.118
- ^ Carbonell F .; Jimenez J.C .; Педросо Л.М. (2008). «Вычисление кратных интегралов с использованием матричных экспонент». J. Comput. Appl. Математика. 213: 300–305. DOI: 10.1016 / j.cam.2007.01.007.
- ^ а б c d Jimenez J.C .; Pedroso L .; Carbonell F .; Эрнандес В. (2006). «Метод локальной линеаризации для численного интегрирования дифференциальных уравнений с запаздыванием». SIAM J. Numer. Анализ. 44 (6): 2584–2609. DOI: 10,1137 / 040607356.
- ^ а б c d е ж Jimenez J.C .; де ла Крус Х. (2012). «Скорость сходимости схем сильной локальной линеаризации для стохастических дифференциальных уравнений с аддитивным шумом». BIT Numer. Математика. 52 (2): 357–382. DOI: 10.1007 / s10543-011-0360-2.
- ^ а б c Jimenez J.C .; Biscay R .; Mora C .; Родригес Л.М. (2002). «Динамические свойства метода локальной линеаризации для начальных задач». Appl. Математика. Comput. 126: 63–68. DOI: 10.1016 / S0096-3003 (00) 00100-4.
- ^ Jimenez J.C .; Сотолонго А .; Санчес-Борнот Дж. М. (2014). «Локально линеаризованный метод Рунге Кутты Дорманда и Принца». Appl. Математика. Comput. 247: 589–606. DOI: 10.1016 / j.amc.2014.09.001.
- ^ Наранхо-Нода, Хименес Дж. К. (2021) «Локально линеаризованный метод Рунге-Кутта Дорманда и Принса для больших систем задач с начальным значением». J.Comput. Физика. DOI: 10.1016 / j.jcp.2020.109946.
- ^ а б c Карбонелл, Ф., Хименес, Дж. К., Бискай, Р. Дж., И Де Ла Круз, Х. (2005). «Метод локальной линеаризации для численного интегрирования случайных дифференциальных уравнений». BIT Num. Математика. 45 (1), 1-14. DOI: 10.1007 / s10543-005-2645-9
- ^ а б Jimenez J.C .; Карбонелл Ф. (2009). «Скорость сходимости схем локальной линеаризации для случайных дифференциальных уравнений». BIT Numer. Математика. 49 (2): 357–373. DOI: 10.1007 / s10543-009-0225-0.
- ^ Хименес Дж. К., Сёдзи И., Одзаки Т. (1999) "Симуляция стохастического дифференциального уравнения с помощью метода локальной линеаризации. Сравнительное исследование". J. Statist. Физика. 99: 587-602 DOI: 10,1023 / А: 1004504506041.
- ^ а б Бискай Р., Хименес Дж. К., Риера Дж. Дж. И Вальдес П. А. (1996). «Метод локальной линеаризации для численного решения стохастических дифференциальных уравнений». Annals Inst. Statis. Математика. 48 (4), 631-644.DOI: 10.1007 / BF00052324
- ^ а б c d е ж грамм de la Cruz H .; Biscay R.J .; Jimenez J.C .; Carbonell F .; Одзаки Т. (2010). «Методы локальной линеаризации высокого порядка: подход к построению A-устойчивых явных схем высокого порядка для стохастических дифференциальных уравнений с аддитивным шумом». BIT Numer. Математика. 50 (3): 509–539. DOI: 10.1007 / s10543-010-0272-6.
- ^ а б c Хименес, Дж. К. (2002). «Простое алгебраическое выражение для оценки схем локальной линеаризации для стохастических дифференциальных уравнений». Appl. Математика. Письма, 15 (6), 775-780.DOI: 10.1016 / S0893-9659 (02) 00041-1
- ^ de la Cruz H .; Jimenez J.C .; Зубелли Дж. П. (2017). «Локально линеаризованные методы моделирования стохастических осцилляторов, управляемых случайными силами». BIT Numer. Математика. 57: 123–151. DOI: 10.1007 / s10543-016-0620-2. S2CID 124662762.
- ^ а б Сёдзи, И., и Одзаки, Т. (1997). «Сравнительное исследование методов оценивания случайных процессов с непрерывным временем». J. Анализ временных рядов. 18 (5), 485-506.DOI: 10.1111 / 1467-9892.00064
- ^ а б c d Jimenez J.C .; Карбонелл Ф. (2015). «Скорость сходимости схем слабой локальной линеаризации для стохастических дифференциальных уравнений с аддитивным шумом». J. Comput. Appl. Математика. 279: 106–122. DOI: 10.1016 / j.cam.2014.10.021.
- ^ а б Carbonell F .; Jimenez J.C .; Бискайский Р.Дж. (2006). «Слабые локальные линейные дискретизации для стохастических дифференциальных уравнений: сходимость и численные схемы». J. Comput. Appl. Математика. 197: 578–596. DOI: 10.1016 / j.cam.2005.11.032.
- ^ Хансен Н. (2003) "Геометрическая эргодичность дискретных аппроксимаций многомерной диффузии". Бернулли. 9: 725-743 DOI: 10.3150 / bj / 1066223276
- ^ Одзаки, Т. (1985). «Нелинейные модели временных рядов и динамические системы». Справочник по статистике, 5, 25-83.DOI: 10.1016 / S0169-7161 (85) 05004-0







![{ displaystyle { frac {d mathbf {x} left (t right)} {dt}} = mathbf {f} left (t, mathbf {x} left (t right) right) ), qquad t in left [t_ {0}, T right], qquad qquad qquad qquad (4.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b689077ae401751f25375eb3338ed66cc57f756a)



![{ displaystyle [t_ {0}, T]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/986ba7ea2bc36ce31beb5c5f4faffbfb6405f69b)


















![{ Displaystyle т ин lbrack t_ {k}, t_ {k + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dacd0fb31482f9ac95b8c3261d9dc00f1055dca4)


![{ displaystyle mathbf {c} = left [c_ {i} right], mathbf {A} = left [a_ {ij} right] quad и quad mathbf {b} = left [ b_ {j} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fbc317004aaf306e62ecc1c6d08e4f49d9d0543)


















![{ displaystyle mathbf {L} = [ mathbf {I} quad mathbf {0} _ {d times l}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75b8ac2636b6ebd86e0bba8f06886336cfc6ec82)
![{ displaystyle mathbf {r} = [ mathbf {0} _ {1 times (d + l-1)} quad 1] ^ { intercal}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e4832a55ccffda573260201924fed69152a784)














![{ displaystyle mathbf {L} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 2} end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05d54f18477ecdb4b717abf25a75b96d17729bcd)
![{ displaystyle mathbf {r} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 1)} & 1 end {array}} верно]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f82230fb66e66705351377690e9f14c8d4a41224)






![{ displaystyle mathbf {T} _ {n} = left [{ begin {array} {cccc} mathbf {f} _ { mathbf {x}} ( mathbf {y} _ {n}) & ( mathbf {I} otimes mathbf {f} ^ { intercal} ( mathbf {y} _ {n})) mathbf {f} _ { mathbf {xx}} ( mathbf {y} _ {n}) mathbf {f} ( mathbf {y} _ {n}) & mathbf {0} & mathbf {f} ( mathbf {y} _ {n}) 0 & 0 & 0 & 0 0 & 0 & 0 & 1 0 & 0 & 0 & 0 end {array}} right] in mathbb {R} ^ {(d + 3) times (d + 3)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04b4535597fcece8be4c40e7b4ae75229d8f9831)
![{ displaystyle mathbf {L} _ {1} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 3} end {array}} right] quad и quad mathbf {r} _ {1} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 2)} & 1 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f495cb0102ab17316c499936bd236cdb35f4ebbd)






![{ displaystyle mathbf {k} _ {1} Equiv mathbf {0}, c = left [{ begin {array} {cccc} 0 & { frac {1} {2}} & { frac { 1} {2}} & 1 end {array}} right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7569810b131c3d8e9ad24b6201f9454d90fbbc)
















![{ displaystyle { frac {d mathbf {x} left (t right)} {dt}} = mathbf {f} left (t, mathbf {x} left (t right), mathbf {x} _ {t} (- tau _ {1}), cdots, mathbf {x} _ {t} (- tau _ {m}) right), qquad t in left [t_ {0}, T right], qquad qquad (5.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/697d2b4993df9f04063023258c020c16b2472d0b)


![{ Displaystyle s in left [- tau, 0 right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36e0323b0f49a9ff410710f3d23bece839ede3f2)
![{ displaystyle mathbf {x} _ {t}: left [- tau, 0 right] longrightarrow mathbb {R} ^ {d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9da7f52b7080c8d8314732acbf3869a6a690a0a6)
![{ displaystyle mathbf {x} _ {t} (s): = mathbf {x} (t + s), { text {}} s in left [- tau, 0 right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57496edc39f42753319edb6dbf8096b2d828dc67)
![{ displaystyle t in left [t_ {0}, T right], mathbf { varphi}: left [- tau, 0 right] longrightarrow mathbb {R} ^ {d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09acb929ae865c8b9aa16afe15c70e21c14caba2)


![{ displaystyle Phi (t_ {n}, mathbf {z} _ {n}, h_ {n}; { widetilde { mathbf {z}}} _ {t_ {n}} ^ {1} ,. ., { widetilde { mathbf {z}}} _ {t_ {n}} ^ {m}) = int limits _ {0} ^ {h_ {n}} e ^ { mathbf {A} _ {n} (h_ {n} -u)} [ sum limits _ {i = 1} ^ {m} mathbf {B} _ {n} ^ {i} ({ widetilde { mathbf {z} }} _ {t_ {n}} ^ {i} left (u- tau _ {i} right) - { widetilde { mathbf {z}}} _ {t_ {n}} ^ {i} left (- tau _ {i} right)) + mathbf {d} _ {n}] du + int limits _ {0} ^ {h_ {n}} int limits _ {0} ^ {u} e ^ { mathbf {A} _ {n} (h_ {n} -u)} mathbf {c} _ {n} drdu}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8033183d307bbeb3a581e56e311a6e526af0fff1)
![{ displaystyle { widetilde { mathbf {z}}} _ {t_ {n}} ^ {i}: left [- tau _ {i}, 0 right] longrightarrow mathbb {R} ^ { d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3f4bc0cc5b10a10d0844d2265aababd5028d6e4)
![{ displaystyle { widetilde { mathbf {z}}} _ {t_ {n}} ^ {i} (s): = { widetilde { mathbf {z}}} ^ {i} (t_ {n} + s), { text {}} s in left [- tau _ {i}, 0 right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6d1f224746bba85bb53d4f2acd5b76b1f50eeef)
![{ displaystyle { widetilde { mathbf {z}}} ^ {i}: left [t_ {n} - tau _ {i}, t_ {n} right] longrightarrow mathbb {R} ^ { d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/922ac10d7369b3ff0ffe9487ebb8a509a1305574)

![{ displaystyle t in lbrack t_ {n} - tau _ {i}, t_ {n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f287009ce5d61c9d7ed2a843c93dfdef6226a50)









![{ Displaystyle и в lbrack 0, h_ {n}])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/956d5d79b8e61251940a26652b1ecead7daa8b6c)






![{ displaystyle mathbf {r} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 1)} & 1 end {array}} справа], h_ {n} leq tau}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05fdb2050667c7b12025db96c59b015211204a57)









![{ displaystyle t in lbrack t_ {0}, t_ {n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ed17e1a454d79e9e85aa3fdb316727d17eb069b)

![{ displaystyle t in left [t_ {0} - tau, t_ {0} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99fafe4165d02d310ce7c3f55c6fbfc1742d2d65)


![{ displaystyle { frac {d mathbf {x} left (t right)} {dt}} = mathbf {f} ( mathbf {x} (t), mathbf { xi} (t) ), quad t in left [t_ {0}, T right], qquad qquad qquad (6.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06e7f4c5cbe530e829f8edf84e2e49d0829a2ef0)





![{ displaystyle t in left [t_ {0}, T right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aedde214e225a352a24c1c922043d56a7d90588b)





![{ displaystyle mathbf {M} _ {n} = left [{ begin {array} {ccc} mathbf {f} _ { mathbf {x}} left ( mathbf {y} _ {n} , mathbf { xi} (t_ {n}) right) & mathbf {f} _ { mathbf { xi}} ( mathbf {y} _ {n}, mathbf { xi} (t_ {n}) ( mathbf { xi} (t_ {n + 1}) - mathbf { xi} (t_ {n})) / h_ {n} & mathbf {f} left ( mathbf { y} _ {n}, mathbf { xi} (t_ {n}) right) 0 & 0 & 1 0 & 0 & 0 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de2e549c00febeadc80e1df68d44a6a66abd159a)






![{ displaystyle d mathbf {x} (t) = mathbf {f} (t, mathbf {x} (t)) dt + sum limits _ {i = 1} ^ {m} mathbf {g} _ {i} (t) d mathbf {w} ^ {i} (t), quad t in left [t_ {0}, T right], qquad qquad qquad (7.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/464be59af5611f27dd6d946030a7202ce481c427)











![{ Displaystyle т ин lbrack t_ {n}, t_ {n + 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b15f801777044ac19f6f4e6551c3e78da54f33c5)













![{ displaystyle mathbf {L} = left [{ begin {array} {ll} mathbf {I} & mathbf {0} _ {d times 2} end {array}} right], mathbf {r} ^ { intercal} = left [{ begin {array} {ll} mathbf {0} _ {1 times (d + 1)} & 1 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4096111183a23671fc2d181a96e16ca7b7df6d6c)


















![{ displaystyle d mathbf {x} (t) = mathbf {f} (t, mathbf {x} (t)) dt + sum limits _ {i = 1} ^ {m} mathbf {g} _ {i} (t) d mathbf {w} ^ {i} (t), qquad t in left [t_ {0}, T right], qquad qquad (8.1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4db0bd45e90a7c91e2715a14caf58e220b2e0b36)







![{ displaystyle mathbf {G} (t) = [ mathbf {g} _ {1} (t), ..., mathbf {g} _ {m} (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9198e9be76ab6056339bf885c5835f38b50399e4)







![{ displaystyle { mathcal {M}} _ {n} = left [{ begin {array} {cccc} mathbf {f} _ { mathbf {x}} (t_ {n}, mathbf {y } _ {n}) & mathbf {GG} ^ { intercal} & mathbf {f} _ {t} (t_ {n}, mathbf {y} _ {n}) & mathbf {f} ( t_ {n}, mathbf {y} _ {n}) mathbf {0} & - mathbf {f} _ { mathbf {x}} ^ { intercal} (t_ {n}, mathbf {y} _ {n}) & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & 0 & 1 mathbf {0} & mathbf {0} & 0 & 0 end {массив}} right] in mathbb {R} ^ {(2d + 2) times (2d + 2)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b6c5cb6cc2c1a036002082a4dcad32b5080660)




![{ displaystyle { mathcal {M}} _ {n} = left [{ begin {array} {cccccc} mathbf {J} & mathbf {H} _ {2} & mathbf {H} _ { 1} & mathbf {H} _ {0} & mathbf {a} _ {2} & mathbf {a} _ {1} mathbf {0} & - mathbf {J} ^ { intercal } & mathbf {I} & mathbf {0} & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & - mathbf {J} ^ { intercal} & mathbf {I} & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & mathbf {0} & - mathbf {J} ^ { intercal} & mathbf {0} & mathbf {0} mathbf {0} & mathbf {0} & mathbf {0} & mathbf {0} & 0 & 1 mathbf {0} & mathbf {0} & mathbf {0} & mathbf {0} & 0 & 0 end {array}} right] in mathbb {R} ^ {(4d + 2) times (4d + 2)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92d5869bcb0a0b5db4944c8170713c0c5a096a6)



