Пара перко - Perko pair
| Пара перко | |
|---|---|
| Инвариант Arf | 1 |
| Длина тесьмы | 10 |
| Тесьма нет. | 3 |
| Мост нет. | 3 |
| Crosscap no. | 2 |
| Переход нет. | 10 |
| Род | 3 |
| Гиперболический объем | 5.63877 |
| Распутывания нет. | 3 |
| Обозначение Конвея | [3:-20:-20] |
| Обозначения A-B | 10161/10162 |
| Обозначение Даукера | 4, 12, -16, 14, -18, 2, 8, -20, -10, -6 |
| Последний / следующий | 10160 / 10162 |
| Другой | |
| гиперболический, волокнистый, основной, обратимый | |
в математическая теория узлов, то Пара перко, названная в честь Кеннета Перко, представляет собой пару записей в классических таблицах узлов, которые фактически представляют один и тот же узел. В Дейл Рольфсен В таблице узлов эта предполагаемая пара различных узлов помечена как 10161 и 10162. В 1973 году, работая над завершением таблиц узлов Тейта – Литтла до 10 пересечений (датируемых концом 19 века),[1] Перко нашел дубликат в Чарльз Ньютон Литтл 'стабильный.[2] Это дублирование было пропущено Джон Хортон Конвей за несколько лет до этого в его узловой таблице, а затем и в таблице Рольфсена.[3] Пара Перко дает контрпример к «теореме», утвержденной Литтлом в 1900 году, что корчиться приведенной диаграммы узла является инвариантом (см. Домыслы Тэйта ), поскольку две диаграммы для пары имеют разные изгибы.
В некоторых более поздних таблицах узлов нумерация узлов немного изменилась (узлы 10163 до 10166 перенумерованы на 10162 до 10165) так что узлов 10161 и 10162 разные. Некоторые авторы ошибочно приняли эти два перенумерованных узла за пару Перко и ошибочно утверждали, что это одно и то же.[4]
- Пара Перко

10161 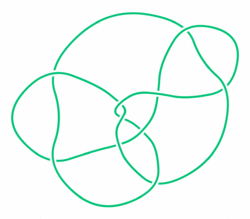
10162 (в исходной нумерации Рольфсена)
Рекомендации
- ^ Чарльз Ньютон Литтл, Непеременные +/- узлы, Пер. Рой. Soc. Эдинбург 39 (1900), стр. 774.
- ^ Кеннет А. Перко младший (р. 1943), О классификации узлов. Proc. Амер. Математика. Soc. 45 (1974), 262–266.
- ^ Дейл Рольфсен, Узлы и ссылки (таблица узлов см. в Приложении C), 1976, ISBN 0-914098-16-0.
- ^ "Месть пары Перко ", RichardElwes.co.uk. По состоянию на февраль 2016 г. Ричард Элвес указывает на распространенную ошибку в описании пары Перко.
внешняя ссылка
- "10_161 ", Узел Атлас.
- Изображения эквивалентности двух узлов: "Парные узлы Perko ", KnotPlot. По состоянию на февраль 2016 г.


