Узел тора - Torus knot



В теория узлов, а торический узел особый вид морской узел лежащий на поверхности незаплетенного тор в р3. Аналогично звено тора это связь которая точно так же лежит на поверхности тора. Каждый торический узел задается парой совмещать целые числа п и q. Зацепление тора возникает, если п и q не взаимно просты (в этом случае количество компонентов равно gcd (р, д)). Торический узел - это банальный (эквивалент без узла) если и только если либо п или же q равно 1 или -1. Простейшим нетривиальным примером является (2,3) -торный узел, также известный как трилистник.

Геометрическое представление
Торический узел может быть геометрически визуализирован несколькими способами: топологически эквивалентный (см. Свойства ниже), но геометрически различны. Условные обозначения, использованные в этой статье и на рисунках, следующие.
(п,q) -торный узел ветра q раз по кругу внутри тора, и п раз вокруг своей оси вращательная симметрия. {Обратите внимание, такое использование ролей p и q противоречит тому, что показано на: http://mathworld.wolfram.com/TorusKnot.html Это также несовместимо с «Списком» торических узлов ниже и с изображениями, которые появляются в: «36 торических узлов», Атлас узлов.} Если п и q не являются взаимно простыми, то мы имеем зацепление тора с более чем одним компонентом.
Направление, в котором нити узла обвиваются вокруг тора, также подлежит различным соглашениям. Чаще всего пряди образуют винт с правой резьбой для p q> 0.[1][2][3]
(п,q) -торный узел может быть задан параметризация
куда и . Он лежит на поверхности тора, задаваемого формулой (в цилиндрические координаты ).
Возможны и другие параметризации, поскольку узлы определены с точностью до непрерывной деформации. Иллюстрации для (2,3) - и (3,8) -торных узлов можно получить, взяв , а в случае (2,3) -торного узла, кроме того, вычитая соответственно и из приведенных выше параметризаций Икс и у. Последний гладко обобщается на любые взаимно простые р, д удовлетворение .
Характеристики

Торический узел - это банальный если только либо п или же q равно 1 или -1.[2][3]
Каждый нетривиальный торический узел является основной[4] и хиральный[2].
(п,q) торический узел эквивалентен (q,п) торический узел.[1][3] Это можно доказать, перемещая нити по поверхности тора.[5] (п,−q) торический узел - это аверс (зеркальное отображение) (п,q) торический узел.[3] (-п,−q) торический узел эквивалентен (п,q) торический узел, за исключением обратной ориентации.

Любой (п,q) -торный узел можно сделать из закрытая коса с п пряди. Соответствующий плести слово является [6]
(Эта формула предполагает общепринятое соглашение, что образующие косы - это прямые скрутки[2][6][7][8] за которым не следует страница Википедии о косичках.)
В номер перехода из (п,q) торический узел с п,q > 0 определяется выражением
- c = мин ((п−1)q, (q−1)п).
В род торического узла с п,q > 0 это
В Полином александра торического узла [1][6]
В Многочлен Джонса (правого) торического узла задается формулой
Дополнение к торическому узлу в 3-сфера это Расслоенное многообразие Зейферта, расслоенная над диском с двумя особыми слоями.
Позволять Y быть п-складывать тупица с диском вынутым из салона, Z быть q-свернутый колпачок с диском снял его внутреннюю часть, и Икс быть факторпространством, полученным отождествлением Y и Z вдоль их граничного круга. Узловое дополнение к (п, q) -торный узел деформация втягивается в космос Икс. Следовательно группа узлов торического узла имеет презентация
Торические узлы - единственные узлы, группы узлов которых имеют нетривиальные центр (который является бесконечным циклическим, порожденным элементом в презентации выше).
В коэффициент растяжения из (п,q) торический узел, как кривая в Евклидово пространство, есть Ω (min (п,q)), поэтому торические узлы имеют неограниченные факторы растяжения. Студент-исследователь Джон Пардон выиграл 2012 Премия Моргана за его исследование, доказывающее этот результат, который решил проблему, первоначально поставленную Михаил Громов.[9][10]
Подключение к сложным гиперповерхностям
(п,q) −торные узлы возникают при рассмотрении зацепления изолированной комплексной особенности гиперповерхности. Комплексную гиперповерхность пересекают с гиперсфера, с центром в изолированной особой точке и с достаточно малым радиусом, чтобы она не охватывала и не сталкивалась с какими-либо другими особыми точками. Пересечение дает подмногообразие гиперсферы.
Позволять п и q быть взаимно простыми целыми числами, большими или равными двум. Рассмотрим голоморфная функция данный Позволять быть набором такой, что Учитывая реальное число мы определяем реальную трехсферу как дано Функция имеет изолированный критическая точка в поскольку если и только если Таким образом, мы рассматриваем структуру рядом с Для этого рассмотрим пересечение Это пересечение является так называемым звеном особенности Ссылка , куда п и q взаимно просты и оба больше или равны двум, это в точности (п,q) −торный узел.[11]
Список

Рисунок справа - торическое звено (72,4).
- Не узел, 31 морской узел (3,2), 51 морской узел (5,2), 71 морской узел (7,2), 819 узел (4,3), 91 морской узел (9,2), 10124 морской узел (5,3)
| Стол # | А-Б | Изображение | п | Q | Крест # |
|---|---|---|---|---|---|
| 0 | 01 |  | 0 | ||
| 3a1 | 31 |  | 3 | 2 | 3 |
| 5a2 | 51 |  | 5 | 2 | 5 |
| 7a7 | 71 |  | 7 | 2 | 7 |
| 8n3 | 819 |  | 4 | 3 | 8 |
| 9a41 | 91 |  | 9 | 2 | 9 |
| 10n21 | 10124 |  | 5 | 3 | 10 |
| 11a367 |  | 11 | 2 | 11 | |
| 13a4878 | 13 | 2 | 13 | ||
 | 7 | 3 | 14 | ||
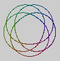 | 5 | 4 | 15 | ||
| 15 | 2 | 15 | |||
 | 8 | 3 | 16 | ||
| 17 | 2 | 17 | |||
| 19 | 2 | 19 | |||
| 10 | 3 | 20 | |||
 | 7 | 4 | 21 | ||
| 21 | 2 | 21 | |||
| 11 | 3 | 22 | |||
| 23 | 2 | 23 | |||
 | 6 | 5 | 24 | ||
| 25 | 2 | 25 | |||
| 13 | 3 | 26 | |||
 | 9 | 4 | 27 | ||
| 27 | 2 | 27 | |||
 | 7 | 5 | 28 | ||
| 14 | 3 | 28 | |||
| 29 | 2 | 29 | |||
| 31 | 2 | 31 | |||
 | 8 | 5 | 32 | ||
| 16 | 3 | 32 | |||
| 11 | 4 | 33 | |||
| 33 | 2 | 33 | |||
| 17 | 3 | 34 | |||
 | 7 | 6 | 35 | ||
| 35 | 2 | 35 | |||
 | 9 | 5 | 36 | ||
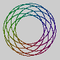 | 8 | 7 | 48 | ||
 | 9 | 7 | 54 | ||
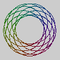 | 9 | 8 | 63 |
грамм-торный узел
А g-торический узел замкнутая кривая, нарисованная на g-тор. С технической точки зрения, это гомеоморфное изображение круга в S³ который может быть реализован как подмножество род грамм ручка в S³. Если связь является подмножеством ручек второго рода, это двойное торическое звено.[12]
Для второго рода простейшим примером двойного торического узла, не являющегося торическим узлом, является узел восьмерка.[13][14]
Смотрите также
Рекомендации
- ^ а б c Ливингстон, Чарльз (1993). Теория узлов. Математическая ассоциация Америки. п.[страница нужна ]. ISBN 0-88385-027-3.
- ^ а б c d Мурасуги, Кунио (1996). Теория узлов и ее приложения. Birkhäuser. п.[страница нужна ]. ISBN 3-7643-3817-2.
- ^ а б c d Каваути, Акио (1996). Обзор теории узлов. Birkhäuser. п.[страница нужна ]. ISBN 3-7643-5124-1.
- ^ Норвуд, Ф. Х. (1 января 1982 г.). «Каждый узел с двумя образующими прост». Труды Американского математического общества. 86 (1): 143–147. Дои:10.1090 / S0002-9939-1982-0663884-7. ISSN 0002-9939. JSTOR 2044414.
- ^ Бейкер, Кеннет (28 марта 2011 г.). "p q is q p". Эскизы топологии. Получено 2020-11-09.
- ^ а б c Ликориш, В. Б. Р. (1997). Введение в теорию узлов. Springer. п.[страница нужна ]. ISBN 0-387-98254-X.
- ^ Дехорной, П .; Дынников, Иван; Рольфсен, Дейл; Уист, Берт (2000). Почему косы можно заказать? (PDF). п.[страница нужна ]. Архивировано из оригинал (PDF) на 2012-04-15. Получено 2011-11-12.
- ^ Birman, J. S .; Брендл, Т. (2005). «Косы: обзор». In Menasco, W .; Thistlethwaite, M. (ред.). Справочник по теории узлов. Эльзевир. п.[страница нужна ]. ISBN 0-444-51452-X.
- ^ Кехо, Элейн (апрель 2012 г.), «Премия Моргана 2012 г.», Уведомления Американского математического общества, 59 (4), стр. 569–571, Дои:10.1090 / noti825.
- ^ Пардон, Джон (2011), "Об искажении узлов на вложенных поверхностях", Анналы математики, Вторая серия, 174 (1), стр. 637–646, arXiv:1010.1972, Дои:10.4007 / летопись.2011.174.1.21, МИСТЕР 2811613
- ^ Милнор, Дж. (1968). Особые точки сложных гиперповерхностей.. Издательство Принстонского университета. п.[страница нужна ]. ISBN 0-691-08065-8.
- ^ Рольфсен, Дейл (1976). Узлы и ссылки. Publish or Perish, Inc. стр.[страница нужна ]. ISBN 0-914098-16-0.
- ^ Хилл, Питер (декабрь 1999 г.). "НА ДВУСТОРОННИХ УЗЛАХ (I)". Журнал теории узлов и ее разветвлений. 08 (08): 1009–1048. Дои:10.1142 / S0218216599000651. ISSN 0218-2165.
- ^ Норвуд, Фредерик (ноябрь 1989 г.). «Кривые на поверхностях». Топология и ее приложения. 33 (3): 241–246. Дои:10.1016/0166-8641(89)90105-3.































