Спинодальный - Spinodal
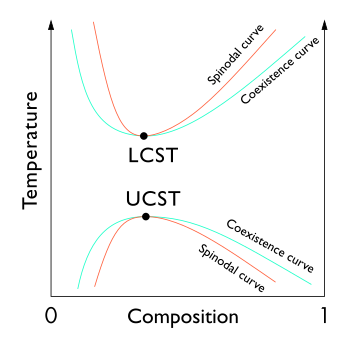
В термодинамика, предел локальной устойчивости по отношению к малым флуктуациям четко определяется условием, что вторая производная свободной энергии Гиббса равна нулю. Геометрическое место этих точек (точка перегиба на кривой G-x или G-c, свободная энергия Гиббса как функция состава) называется точкой перегиба. спинодальный изгиб.[1][2][3] Для составов внутри этой кривой бесконечно малые колебания состава и плотности приведут к разделению фаз через спинодальный распад. Вне кривой решение будет как минимум метастабильным по отношению к флуктуациям.[3] Другими словами, вне спинодали некоторый осторожный процесс может получить однофазную систему.[3] Внутри него только процессы, далекие от термодинамического равновесия, такие как физическое осаждение из паровой фазы, позволят получать однофазные композиции.[4] Локальные точки сосуществующих композиций, определяемые общей касательной конструкцией, известны как бинодальный (сосуществование) кривая, которая обозначает состояние равновесия системы с минимальной энергией. Повышение температуры приводит к уменьшению разницы между энтропией смешения и энтальпией смешения, и, таким образом, сосуществующие составы становятся ближе. Бинодальная кривая составляет основу разрыв в смешиваемости на фазовой диаграмме. Свободная энергия смешения изменяется с температурой и концентрацией, и бинодали и спинодали встречаются на критическая или абсолютная температура и состав.[5]
Критерий
Для бинарных растворов термодинамический критерий, определяющий спинодальную кривую, состоит в том, что вторая производная свободной энергии по плотности или некоторой переменной состава равна нулю.[3][6][7]
Критическая точка
Экстремумы спинодали на графике зависимости температуры от состава совпадают с экстремумами бинодали и известны как критические точки.[7]
Изотермическое равновесие жидкость-жидкость
В случае тройного изотермического равновесия жидкость-жидкость, спинодальная кривая (полученная из матрицы Гессе) и соответствующая критическая точка могут использоваться, чтобы помочь процессу корреляции экспериментальных данных.[8][9][10]
использованная литература
- ^ Г. Астарита: Термодинамика: расширенный учебник для инженеров-химиков (Springer 1990), главы 4, 8, 9, 12.
- ^ Сандлер С. И., Химическая и инженерная термодинамика. 1999 г., John Wiley & Sons, Inc., стр. 571.
- ^ а б c d Конингсвельд К., Штокмайер В. Х., Нис Э., Фазовые диаграммы полимеров: Учебник. 2001 Оксфорд, стр. 12.
- ^ P.H. Mayrhofer et al. Успехи материаловедения 51 (2006) 1032-1114 Дои:10.1016 / j.pmatsci.2006.02.002
- ^ Кан Р.В., Хаасен П. Металлургия. 4-е изд. Кембридж: Univ Press; 1996 г.
- ^ Сандлер С. И., Химическая и инженерная термодинамика. 1999 г., John Wiley & Sons, Inc., стр. 557.
- ^ а б Конингсвельд К., Штокмайер В. Х., Нис Э., Фазовые диаграммы полимеров: Учебник. 2001 Oxford, стр 46-47.
- ^ Марсилла, А .; Серрано, доктор медицины; Reyes-Labarta, J.A .; Олая, М. (2012). «Проверка условий критической точки жидкость-жидкость и их применение в тройных системах». Промышленные и инженерные химические исследования. 51 (13): 5098–5102. Дои:10.1021 / ie202793r.
- ^ Марсилла, А .; Reyes-Labarta, J.A .; Серрано, доктор медицины; Олая, М. (2011). "Модели и алгоритмы GE для регрессии данных равновесия конденсированных фаз в тройных системах: ограничения и предложения". Открытый журнал термодинамики. 5: 48–62. Дои:10.2174 / 1874396X01105010048.
- ^ Графический интерфейс пользователя (GUI) (27 ноября 2015 г.). «Топологический анализ функции энергии Гиббса (данные о корреляции между жидкостью и жидкостью. Включая термодинамический обзор и анализ связующих линий / матрицы Гессе)». Университет Аликанте (Рейес-Лабарта и др., 2015-18). HDL:10045/51725. Цитировать журнал требует
| журнал =(Помогите)

