Диэдральная группа порядка 6 - Dihedral group of order 6
эта статья может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к Сделайте это понятным для неспециалистов, не снимая технических деталей. (Апрель 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |


(Генераторы а и б такие же, как на графике Кэли, показанном выше.)


Только нейтральные элементы симметричны главной диагонали, поэтому эта группа не является абелевский.

В математика, D3 (иногда альтернативно обозначается как D6) это группа диэдра степени 3, или, другими словами, диэдральная группа порядок 6. Он изоморфен симметричная группа S3 степени 3. Это также минимально возможный неабелева группа.[1]
Эта страница иллюстрирует многие концепции группы на примере этой группы.
Группы симметрии
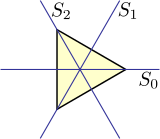
Группа диэдра D3 это группа симметрии из равносторонний треугольник, то есть это набор всех преобразований, таких как отражение, вращение и их комбинации, которые оставляют форму и положение этого треугольника неизменными. В случае D3, всевозможные перестановка вершин треугольника составляет такое преобразование, так что группа этих симметрий равна изоморфный симметрической группе S3 всех перестановок трех различных элементов. Это не относится к группам диэдра высших порядков.
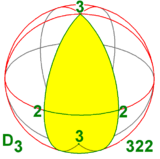
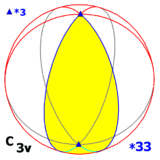
Группа диэдра D3 изоморфна двум другим группам симметрии в трех измерениях:
- один с 3-кратной осью вращения и перпендикулярной 2-кратной осью вращения (отсюда три из них): D3
- один с 3-кратной осью вращения в плоскости отражения (и, следовательно, также в двух других плоскостях отражения): C3в
Перестановки набора из трех объектов
Рассмотрим три цветных блока (красный, зеленый и синий), изначально размещенные в порядке RGB. В симметричная группа S3 тогда группа всех возможных перестановки этих блоков. Если обозначить через а действие «поменять местами первые два блока», и б действие «поменять местами последние два блока», мы можем записать все возможные перестановки в терминах этих двух действий.
В мультипликативной форме мы традиционно пишем ху для комбинированного действия "сначала сделайте у, тогда сделай Икс"; так что ab это действие RGB ↦ RBG ↦ BRG, т.е. "взять последний блок и переместить его на передний план". Если мы напишем е вместо "оставить блоки такими, какие они есть" (тождественное действие), мы можем написать шесть перестановки из набор из трех блоков как следующие действия:
- е : RGB ↦ RGB или ()
- а : RGB ↦ GRB или (RG)
- б : RGB ↦ RBG или (ГБ)
- ab : RGB ↦ BRG или (RBG)
- ба : RGB ↦ GBR или (RGB)
- аба : RGB ↦ BGR или (RB)
Обозначения в скобках - это обозначение цикла.
Обратите внимание, что действие аа имеет эффект RGB ↦ GRB ↦ RGB, оставив блоки как есть; так что мы можем написать аа = е.Так же,
- bb = е,
- (аба)(аба) = е, и
- (ab)(ба) = (ба)(ab) = е;
поэтому каждое из вышеуказанных действий имеет обратное.
Путем осмотра мы также можем определить ассоциативность и закрытие (два из необходимых групповые аксиомы ); обратите внимание, например, что
- (ab)а = а(ба) = аба, и
- (ба)б = б(ab) = бабушка.
Группа неабелева, поскольку, например, ab ≠ ба. Поскольку он построен из основных действий а и б, мы говорим, что множество {а, б} генерирует Это.
Группа имеет презентация
- , также написано
- или
- , также написано
где а и б свопы и р = ab - циклическая перестановка. Обратите внимание, что вторая презентация означает, что группа является Группа Кокстера. (Фактически, все диэдральные группы и группы симметрии являются группами Кокстера.)
Сводка групповых операций
С генераторами а и б, мы определяем дополнительные сокращения c := аба, d := ab и ж := ба, так что а, б, в, г, д, и ж все элементы этой группы. Затем мы можем суммировать групповые операции в виде Стол Кэли:
| * | е | а | б | c | d | ж |
|---|---|---|---|---|---|---|
| е | е | а | б | c | d | ж |
| а | а | е | d | ж | б | c |
| б | б | ж | е | d | c | а |
| c | c | d | ж | е | а | б |
| d | d | c | а | б | ж | е |
| ж | ж | б | c | а | е | d |
Обратите внимание, что только неравные неидентичные элементы ездить если они противоположны друг другу. Следовательно, группа бесцентровый, т.е. центр группы состоит только из единичного элемента.
Классы сопряженности
Мы можем легко выделить три вида перестановок трех блоков: классы сопряженности группы:
- no change (), групповой элемент порядок 1
- меняя местами два блока: (RG), (RB), (GB), три групповых элемента порядка 2
- циклическая перестановка всех трех блоков: (RGB), (RBG), два групповых элемента порядка 3
Например, (RG) и (RB) оба имеют форму (Икс у); перестановка букв R, G и B (а именно (GB)) меняет обозначение (RG) на (RB). Следовательно, если мы применим (GB), затем (RB), а затем обратное к (GB), которое также является (GB), в результате перестановка будет (RG).
Обратите внимание, что элементы сопряженной группы всегда имеют одинаковые порядок, но в общем случае два элемента группы, которые имеют одинаковый порядок, не обязательно должны быть сопряжены.
Подгруппы
Из Теорема Лагранжа мы знаем, что любой нетривиальный подгруппа группы из 6 элементов должны иметь порядок 2 или 3. Фактически, два циклические перестановки всех трех блоков, с единицей, образуют подгруппу порядка 3, показатель 2, и перестановки двух блоков, каждый с идентичностью, образуют три подгруппы порядка 2, индекс 3. Существование подгрупп порядка 2 и 3 также является следствием Теорема Коши.
Первый из них {(), (RGB), (RBG)}, то переменная группа А3.
Слева смежные классы и правые классы класса A3 совпадают (как и для любой подгруппы индекса 2) и состоят из A3 и набор из трех свопов {(RB), (RG), (BG)}.
Левые смежные классы {(), (RG)} находятся:
- {(), (RG)}
- {(RB), (RGB)}
- {(GB), (RBG)}
Правильные классы {(RG), ()} находятся:
- {(RG), ()}
- {(RBG), (RB)}
- {(RGB), (GB)}
Таким образом, A3 является нормальный, а остальные три нетривиальные подгруппы - нет. В факторгруппа г / А3 изоморфен C2.
, а полупрямой продукт, где ЧАС представляет собой подгруппу из двух элементов: () и одного из трех свопов. Это разложение также является следствием (частным случаем) Теорема Шура – Цассенхауза.
В терминах перестановок два групповых элемента г / А3 это набор даже перестановки и набор нечетных перестановок.
Если исходная группа - это группа, созданная поворотом плоскости вокруг точки на 120 ° и отражением относительно прямой, проходящей через эту точку, то фактор-группа имеет два элемента, которые можно описать как подмножества «просто повернуть ( или ничего не делать) "и" возьмите зеркальное изображение ".
Отметим, что для группы симметрии квадрат, неравномерная перестановка вершин делает нет соответствуют получению зеркального изображения, но не разрешенным операциям прямоугольники, то есть поворот на 90 ° и применение диагональной оси отражения.
Полупрямые продукты
является если оба φ(0) и φ(1) тождественны. Полупрямое произведение изоморфно группе диэдра порядка 6, если φ(0) - тождество и φ(1) - нетривиальный автоморфизм C3, который инвертирует элементы.
Таким образом получаем:
- (п1, 0) * (п2, час2) = (п1 + п2, час2)
- (п1, 1) * (п2, час2) = (п1 − п2, 1 + час2)
для всех п1, п2 в C3 и час2 в C2. Более кратко,
для всех п1, п2 в C3 и час1, час2 в C2.
В таблице Кэли:
| 00 | 10 | 20 | 01 | 11 | 21 | |
|---|---|---|---|---|---|---|
| 00 | 00 | 10 | 20 | 01 | 11 | 21 |
| 10 | 10 | 20 | 00 | 11 | 21 | 01 |
| 20 | 20 | 00 | 10 | 21 | 01 | 11 |
| 01 | 01 | 21 | 11 | 00 | 20 | 10 |
| 11 | 11 | 01 | 21 | 10 | 00 | 20 |
| 21 | 21 | 11 | 01 | 20 | 10 | 00 |
Обратите внимание, что для второй цифры у нас фактически есть таблица 2 × 2 с 3 × 3 равными значениями для каждой из этих 4 ячеек. Для первой цифры левая половина таблицы такая же, как правая половина, но верхняя половина отличается от нижней.
Для непосредственный product таблица такая же, за исключением того, что первые цифры в нижней половине таблицы такие же, как в верхней половине.
Групповое действие
Эта секция нуждается в расширении с: диаграммой. Вы можете помочь добавляя к этому. (Апрель 2015 г.) |
Учитывать D3 геометрическим способом, как группа симметрии из изометрии плоскости, и рассмотрим соответствующие групповое действие на наборе из 30 равномерно расположенных точек на окружности, пронумерованных от 0 до 29, с 0 на одной из осей отражения.
В этом разделе показаны концепции групповых действий для этого случая.
Действие г на Икс называется
- переходный если для любых двух Икс, у в Икс существует грамм в г такой, что грамм · Икс = у; это не тот случай
- верный (или же эффективный) если для любых двух разных грамм, час в г существует Икс в Икс такой, что грамм · Икс ≠ час · Икс; это так, потому что, кроме тождества, группы симметрии не содержат элементов, которые "ничего не делают"
- свободный если для любых двух разных грамм, час в г и все Икс в Икс у нас есть грамм · Икс ≠ час · Икс; это не так, потому что есть отражения
Орбиты и стабилизаторы

В орбита точки Икс в Икс это набор элементов Икс которому Икс могут перемещаться элементами г. Орбита Икс обозначается Gx:
Орбиты {0, 10, 20}, {1, 9, 11, 19, 21, 29}, {2, 8, 12, 18, 22, 28}, {3, 7, 13, 17, 23, 27}, {4, 6, 14, 16, 24, 26}, и {5, 15, 25}. Точки на орбите «эквивалентны». Если к узору применяется группа симметрии, то внутри каждой орбиты цвет будет одинаковым.
Множество всех орбит Икс под действием г записывается как Икс / г.
Если Y это подмножество из Икс, мы пишем GY для набора { грамм · у : у ∈ Y и грамм ∈ г }. Мы называем подмножество Y инвариантен относительно G если GY = Y (что эквивалентно GY ⊆ Y). В этом случае, г также работает на Y. Подмножество Y называется фиксируется под G если грамм · у = у для всех грамм в г и все у в Y. Союз, например, две орбиты инвариантны относительно г, но не исправлено.
Для каждого Икс в Икс, мы определяем подгруппа стабилизатора из Икс (также называемый группа изотропии или маленькая группа) как набор всех элементов в г это исправление Икс:
Если Икс это точка отражения (0, 5, 10, 15, 20 или 25), его стабилизатором является группа второго порядка, содержащая тождество и отражение в Икс. В остальных случаях стабилизатор - тривиальная группа.
Для фиксированного Икс в Икс, рассмотрим карту из г к Икс данный грамм ↦ грамм · Икс. В изображение этой карты - орбита Икс и coimage это набор всего, что осталось смежные классы из гИкс. Стандартная фактор-теорема теории множеств затем дает естественное биекция между г / гИкс и Gx. В частности, биекция дается формулой hGИкс ↦ час · Икс. Этот результат известен как теорема о стабилизаторе орбиты. В двух случаях малой орбиты стабилизатор нетривиален.
Если два элемента Икс и у принадлежат одной орбите, то их стабилизирующие подгруппы, гИкс и гу, находятся изоморфный. Точнее: если у = грамм · Икс, тогда гу = gGИкс грамм−1. В примере это применимо, например, для 5 и 25 - обе точки отражения. Отражение около 25 соответствует повороту на 10, отражение около 5 и повороту на -10.
Результат, тесно связанный с теоремой о стабилизаторе орбиты: Лемма Бернсайда:
где Иксграмм - это множество точек, зафиксированных грамм. То есть количество орбит равно среднему количеству точек, зафиксированных на один элемент группы.
Для тождества все 30 точек фиксированы, для двух вращений - нет, а для трех отражений - по два на каждое: {0, 15}, {5, 20}, и {10, 25}. Таким образом, среднее число витков составляет шесть.
Теория представлений
С точностью до изоморфизма эта группа имеет три неприводимых комплексных унитарных представления, которые мы будем называть (тривиальное представление), и , где нижний индекс указывает размер. По своему определению как группа перестановок над множеством из трех элементов, группа имеет представление на путем перестановки элементов вектора, фундаментального представления. Это представление не является неприводимым, поскольку оно разлагается как прямая сумма и . появляется как подпространство векторов вида и - представление на его ортогональном дополнении, которые являются векторами вида Нетривиальное одномерное представление возникает через группы оценка: Действие - это умножение на знак перестановки элемента группы. Каждая конечная группа имеет такое представление, поскольку по своему регулярному действию является подгруппой циклической группы. Считая квадратные размеры представлений (, порядок группы), мы видим, что это должны быть все неприводимые представления.[2]
2-мерное неприводимое линейное представление дает 1-мерное проективное представление (т. Е. действие на проективной линии, вложение в Группа Мебиуса PGL (2, C)), так как эллиптические преобразования. Это может быть представлено матрицами с элементами 0 и ± 1 (здесь записано как дробно-линейные преобразования ), известный как ангармоническая группа:
- порядок 1:
- заказ 2:
- заказ 3:
и, таким образом, спускается к представлению над любым полем, которое всегда является точным / инъективным (поскольку никакие два термина не отличаются только знаком). Над полем с двумя элементами проективная линия имеет только 3 точки, и, таким образом, это исключительный изоморфизм В характеристике 3 это вложение стабилизирует точку поскольку (в характеристике больше 3 эти точки различны и переставлены, и являются орбитой гармоническое поперечное отношение ). Над полем с тремя элементами проективная линия имеет 4 элемента, и поскольку PGL (2, 3) изоморфна симметрической группе на 4 элементах, S4, результирующее вложение равняется стабилизатору точки .
Смотрите также
Рекомендации
- ^ Кубо, Дзисуке (2008 г.), «Диэдральная группа как семейная группа», Квантовая теория поля и не только, World Sci. Publ., Hackensack, NJ, pp. 46–63, Дои:10.1142/9789812833556_0004, Г-Н 2588575. Для идентификации D3 с S3, и наблюдение, что эта группа является наименьшей возможной неабелевой группой, см. п. 49.
- ^ Вайсштейн, Эрик В. "Двугранная группа D3". MathWorld.
- Фрали, Джон Б. (1993), Первый курс абстрактной алгебры (5-е изд.), Addison-Wesley, pp. 93–94, ISBN 978-0-201-53467-2
























![-1=[-1:1],](https://wikimedia.org/api/rest_v1/media/math/render/svg/8727e7f63f9d58792bf9c249178c529b1741d8be)


