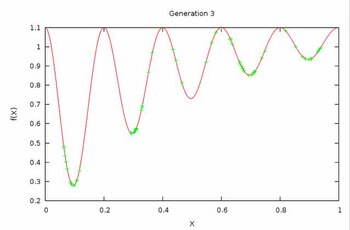
Эволюционная мультимодальная оптимизация - Evolutionary multimodal optimization
В Прикладная математика, мультимодальная оптимизация имеет дело с оптимизация задачи, которые включают поиск всех или большей части множества (по крайней мере, локально оптимальных) решений проблемы, в отличие от одного лучшего решения. Эволюционная мультимодальная оптимизация - это ветвь эволюционные вычисления, который тесно связан с машинное обучение. Вонг дает краткий обзор,[1] где глава Шира[2] и книга Прейса[3] осветить тему более подробно.
Мотивация
Знание множества решений задачи оптимизации особенно полезно в инженерии, когда из-за физических (и / или финансовых) ограничений не всегда удается достичь лучших результатов. В таком сценарии, если известно несколько решений (локально и / или глобально оптимальных), реализацию можно быстро переключить на другое решение и при этом получить максимально возможную производительность системы. Множественные решения также могут быть проанализированы для обнаружения скрытых свойств (или взаимосвязей) основной проблемы оптимизации, что делает их важными для получения базовые знания. Кроме того, алгоритмы мультимодальной оптимизации обычно не только определяют местонахождение нескольких оптимумов за один прогон, но также сохраняют их популяционное разнообразие, что приводит к их способности глобальной оптимизации мультимодальных функций. Более того, методы мультимодальной оптимизации обычно заимствуются как методы поддержания разнообразия для решения других задач.[4]
Фон
Классические методы оптимизации потребуют нескольких точек перезапуска и нескольких запусков в надежде, что при каждом запуске будет обнаружено новое решение, однако без гарантии. Эволюционные алгоритмы (EAs) благодаря подходу, основанному на популяциях, обеспечивают естественное преимущество перед классическими методами оптимизации. Они поддерживают совокупность возможных решений, которые обрабатываются в каждом поколении, и если несколько решений могут быть сохранены на протяжении всех этих поколений, то при завершении алгоритма у нас будет несколько хороших решений, а не только лучшее решение. Обратите внимание, что это противоречит естественной тенденции классических методов оптимизации, которые всегда сходятся к лучшему или субоптимальному решению (в надежной, «плохо работающей» функции). обнаружение и поддержание из нескольких решений заключается в том, что проблема использования советников для мультимодальной оптимизации. Niching[5] это общий термин, называемый техникой поиска и сохранения нескольких стабильных ниши, или благоприятные части пространства решений, возможно, вокруг нескольких решений, чтобы предотвратить сходимость к одному решению.
Поле Эволюционные алгоритмы охватывает генетические алгоритмы (ГА), стратегия эволюции (ES), дифференциальная эволюция (DE), оптимизация роя частиц (PSO) и другие методы. Были предприняты попытки решить многомодальную оптимизацию во всех этих сферах и в большинстве, если не во всех, различных методах, реализующих ничинг в той или иной форме.
Мультимодальная оптимизация с использованием генетических алгоритмов / стратегий эволюции
Метод скучивания Де Йонга, подход с функцией разделения Голдберга, метод клиринга Петровски, ограниченное спаривание, поддержание нескольких субпопуляций - вот некоторые из популярных подходов, которые были предложены сообществом. Первые два метода особенно хорошо изучены, однако в них нет явного разделения на решения, принадлежащие разным областям притяжения.
Применение мультимодальной оптимизации в ES не было явным в течение многих лет и было исследовано только недавно. Шир, представил фреймворк niching, использующий дерандомизированный ES,[6] предлагая CMA-ES как оптимизатор niching впервые. В основе этой структуры лежал выбор индивидуального пика для каждой субпопуляции в каждом поколении с последующей его выборкой для получения последовательного разброса точек поиска. В биологическая аналогия этого оборудования Альфа-самец победа во всех объявленных соревнованиях и последующее доминирование экологическая ниша, который затем получает все сексуальные ресурсы, чтобы произвести потомство.
Недавно эволюционный многокритериальная оптимизация (EMO) подход был предложен,[7] в котором подходящая вторая цель добавляется к исходной единственной задаче мультимодальной оптимизации, так что несколько решений образуют слабый парето-оптимальный передний. Следовательно, проблема мультимодальной оптимизации может быть решена для ее нескольких решений с использованием алгоритма EMO. Улучшая свою работу,[8] те же авторы сделали свой алгоритм самонастраивающимся, что устраняет необходимость в предварительном задании параметров.
В статье предлагается подход, который не использует какой-либо радиус для разделения популяции на субпопуляции (или виды), а вместо этого использует топологию пространства.[9]
Рекомендации
- ^ Вонг, К. С. (2015), Эволюционная мультимодальная оптимизация: краткий обзор Препринт arXiv arXiv: 1508.00457
- ^ Шир, О. (2012), Ничинга в эволюционных алгоритмах В архиве 2016-03-04 в Wayback Machine
- ^ Прейсс, Майк (2015), Мультимодальная оптимизация с помощью эволюционных алгоритмов
- ^ Wong, K. C. et al. (2012), Эволюционная мультимодальная оптимизация с использованием принципа локальности Информационные науки
- ^ Махфуд, С. В. (1995), "Методы Ничинга для генетических алгоритмов "
- ^ Шир, О. (2008), "Ничинга в стратегии дерандомизированной эволюции и ее приложениях в квантовом управлении "
- ^ Деб, К., Саха, А. (2010) "Нахождение множественных решений для задач мультимодальной оптимизации с использованием многоцелевого эволюционного подхода "(GECCO 2010, в печати)
- ^ Саха, А., Деб, К. (2010) «Двухкритериальный подход к мультимодальной оптимизации: самоадаптивный подход» (конспект лекций по информатике, 2010 г., том 6457/2010, 95–104)
- ^ К. Стоуан, М. Прейсс, Р. Стоуан, Д. Думитреску (2010) Мультимодальная оптимизация с помощью алгоритма сохранения топологических видов. В IEEE Transactions on Evolutionary Computing, Vol. 14, выпуск 6, страницы 842–864, 2010 г.
Библиография
- Д. Голдберг и Дж. Ричардсон. (1987) "Генетические алгоритмы с совместным использованием для оптимизации мультимодальных функций ". В Трудах Второй Международной конференции по генетическим алгоритмам по генетическим алгоритмам и их оглавлению применения, страницы 41–49. L. Erlbaum Associates Inc., Хиллсдейл, Нью-Джерси, США, 1987.
- А. Петровский. (1996) "Процедура клиринга как метод определения генетических алгоритмов ". В материалах Международной конференции IEEE 1996 г. по эволюционным вычислениям, страницы 798–803. Citeseer, 1996.
- Деб, К., (2001) «Многоцелевая оптимизация с использованием эволюционных алгоритмов», Wiley (Google Книги)
- Ф. Штрайхерт, Г. Штейн, Х. Ульмер и А. Целл. (2004) "Советник niching на основе кластеризации для пространств мультимодального поиска Лекционные заметки по информатике, страницы 293–304, 2004 г.
- Сингх, Г., Деб, К., (2006) "Сравнение алгоритмов мультимодальной оптимизации на основе эволюционных алгоритмов ". В материалах 8-й ежегодной конференции по генетическим и эволюционным вычислениям, страницы 8–12. ACM, 2006.
- Ронкконен, Дж. (2009). Непрерывная мультимодальная глобальная оптимизация с помощью методов, основанных на дифференциальной эволюции
- Вонг, К. С. (2009). Эволюционный алгоритм с видоспецифическим взрывом для мультимодальной оптимизации. GECCO 2009: 923–930
- Дж. Баррера и К. А. С. Коэльо. "Обзор методов оптимизации роя частиц, используемых для мультимодальной оптимизации ", страницы 9–37. Springer, Берлин, ноябрь 2009 г.
- Вонг, К. С. (2010). Влияние пространственной локальности на эволюционный алгоритм мультимодальной оптимизации. EvoApplications (1) 2010: 481–490
- Деб, К., Саха, А. (2010) Нахождение множественных решений для задач мультимодальной оптимизации с использованием многоцелевого эволюционного подхода. GECCO 2010: 447–454
- Вонг, К. С. (2010). Прогнозирование структуры белка на решеточной модели с помощью методов мультимодальной оптимизации. GECCO 2010: 155–162
- Саха, А., Деб, К. (2010), Двухкритериальный подход к мультимодальной оптимизации: самоадаптивный подход. SEAL 2010: 95–104
- Шир, О.М., Эммерих, М., Бэк, Т. (2010), Подходы к адаптивным радиусам и формам ниши для нишинга с помощью CMA-ES. Эволюционные вычисления Vol. 18, No. 1, pp. 97-126.
- К. Стоуан, М. Прейсс, Р. Стоуан, Д. Думитреску (2010) Мультимодальная оптимизация с помощью алгоритма сохранения топологических видов. В IEEE Transactions on Evolutionary Computing, Vol. 14, выпуск 6, страницы 842–864, 2010 г.
- С. Дас, С. Мэйти, Би-И Ку, П. Н. Сугантан "Эволюционная мультимодальная оптимизация с использованием реальных параметров - Обзор современного состояния ", Vol. 1, No. 2, pp. 71–88, Swarm and Evolutionary Computing, июнь 2011 г.