Диаграмма Смита - Smith chart

В Диаграмма Смита, изобретенный Филлип Х. Смит (1905–1987),^[1][2] и Т. Мидзухаси,^[3] графический калькулятор или номограмма предназначен для инженеры-электрики и электронщики специализируясь на радиочастота (RF) инжиниринг для помощи в решении проблем с линии передачи и соответствие схемы.^[4][5] Диаграмму Смита можно использовать для одновременного отображения нескольких параметров, включая сопротивление, допуски, коэффициенты отражения, ${ Displaystyle S_ {nn} ,}$ параметры рассеяния, коэффициент шума круги, контуры постоянного усиления и области для безусловная стабильность, в том числе механические вибрации анализ.^{[6][7]:93–103} Диаграмма Смита наиболее часто используется в области единичного радиуса или внутри нее. Тем не менее, остаток по-прежнему имеет математическое значение, поскольку используется, например, в осциллятор дизайн и стабильность анализ.^[7]:98–101Хотя использование бумажных диаграмм Смита для решения сложной математики, связанной с задачами сопоставления, в значительной степени было заменено методами, основанными на программном обеспечении, диаграмма Смита по-прежнему остается очень полезным методом демонстрации ^[8] как RF-параметры ведут себя на одной или нескольких частотах, альтернатива использованию табличный Информация. Таким образом, большинство программного обеспечения для анализа ВЧ-цепей включает в себя вариант диаграммы Смита для отображения результатов, и все, кроме простейших приборов для измерения импеданса, могут отображать результаты измерений на дисплее диаграммы Смита.^[9]

Диаграмма Смита импеданса (без графических данных)

Обзор

А сетевой анализатор (HP 8720A) с диаграммой Смита.

Диаграмма Смита нанесена на сложный коэффициент отражения самолет в два измерения и масштабируется в нормализованном сопротивление (самый распространенный), нормализованный допуск или оба, используя разные цвета, чтобы различать их. Их часто называют диаграммами Смита Z, Y и YZ соответственно.^[7]:97 Нормализованное масштабирование позволяет использовать диаграмму Смита для задач, связанных с любыми характеристика или полное сопротивление системы, представленное центральной точкой диаграммы. Наиболее часто используемый импеданс нормализации составляет 50Ом. Как только ответ получен с помощью графических построений, описанных ниже, можно легко преобразовать между нормализованным импедансом (или нормализованной проводимостью) и соответствующим ненормализованным значением путем умножения на характеристический импеданс (проводимость). Коэффициенты отражения можно прочитать прямо из диаграммы, поскольку они являются безразмерными параметрами.

На диаграмме Смита есть шкала вокруг длина окружности или периферия, которая закончена в длины волн и градусы. Шкала длин волн используется в распределенный компонент проблем и представляет собой расстояние, измеренное вдоль линии передачи, соединенной между генератор или источник и нагрузка на рассматриваемую точку. Шкала в градусах представляет угол коэффициента отражения напряжения в этой точке. Диаграмма Смита также может использоваться для сосредоточенный элемент проблемы сопоставления и анализа.

Использование диаграммы Смита и интерпретация полученных с ее помощью результатов требует хорошего понимания Теория цепей переменного тока и теория линий передачи, оба из которых являются предпосылками для инженеров РФ.

Поскольку полное и полное сопротивление изменяется с частотой, проблемы с использованием диаграммы Смита могут быть решены только вручную с помощью одного частота за один раз, результат представлен точка. Часто этого достаточно для узкая полоса приложений (обычно от 5% до 10% пропускная способность ), но для более широких полос частот обычно необходимо применять методы диаграммы Смита на более чем одной частоте в рабочей полосе частот. Если частоты достаточно близки, полученные точки диаграммы Смита могут быть соединены прямыми линиями, чтобы создать локус.

Геометрическое место точек на диаграмме Смита, охватывающее диапазон частот, можно использовать для визуального представления:

• как емкостной или как индуктивный нагрузка находится в частотном диапазоне
• насколько сложным может быть согласование на разных частотах
• насколько хорошо согласован конкретный компонент.

Точность диаграммы Смита снижается для задач, включающих большое количество импедансов или проводимых сопротивлений, хотя масштабирование может быть увеличено для отдельных областей, чтобы учесть их.

Математическая основа

Базовое использование диаграммы Смита импеданса. Волна спускается по линия передачи из характеристическое сопротивление Z₀, завершается при нагрузке с сопротивление Z_L и нормализованный импеданс z=Z_L/Z₀. Существует отражение сигнала с коэффициентом Γ. Каждая точка на диаграмме Смита одновременно представляет собой значение z (внизу слева) и соответствующее значение Γ (внизу справа), связанное соотношением z= (1 + Γ) / (1 - Γ).

Фактический и нормализованный импеданс и проводимость

Линия передачи с волновым сопротивлением ${ Displaystyle Z_ {0} ,}$ можно повсеместно считать имеющим характерный допуск из ${ displaystyle Y_ {0} ,}$ куда

${ displaystyle Y_ {0} = { frac {1} {Z_ {0}}} ,}$

Любое сопротивление, ${ Displaystyle Z _ { текст {T}} ,}$ выраженное в омах, может быть нормализовано путем деления на характеристический импеданс, поэтому нормированный импеданс в нижнем регистре z_Т дан кем-то

${ displaystyle z _ { text {T}} = { frac {Z _ { text {T}}} {Z_ {0}}} ,}$

Аналогично для нормализованного допуска

${ displaystyle y _ { text {T}} = { frac {Y _ { text {T}}} {Y_ {0}}} ,}$

В Единица СИ из сопротивление это ом с символом верхнего регистра Греческая буква омега (Ω) и Единица СИ за допуск это Сименс с символом заглавной буквы S. Нормированный импеданс и нормализованная проводимость равны безразмерный. Фактические импедансы и допуски должны быть нормализованы перед их использованием на диаграмме Смита. Как только результат получен, его можно ненормализовать, чтобы получить фактический результат.

Диаграмма Смита с нормализованным импедансом

Линии передачи оканчиваются обрывом (вверху) и коротким замыканием (внизу). Импульс идеально отражается от обоих оконечных устройств, но знак отраженного напряжения в обоих случаях противоположен. Черные точки обозначают электроны, а стрелки показывают электрическое поле.

Используя теорию линии передачи, если линия передачи прекращено в импедансе (${ Displaystyle Z _ { текст {T}} ,}$), который отличается от его характеристического импеданса (${ Displaystyle Z_ {0} ,}$), а стоячая волна будет сформирована на линии, включающей результирующий как инцидента, так и жили вперед (${ Displaystyle V _ { текст {F}} ,}$) и ротраженный или перевернутый (${ Displaystyle V _ { текст {R}} ,}$) волны. С помощью сложный экспоненциальный обозначение:

${ Displaystyle В _ { текст {F}} = А ехр (J омега т) ехр (+ гамма ell) ~ ,}$ и

${ Displaystyle В _ { текст {R}} = В ехр (J омега т) ехр (- гамма ell) ,}$

куда

${ Displaystyle ехр (J омега т) ,}$ это временный часть волны

${ Displaystyle ехр ( пм гамма ell) ,}$ - пространственная часть волны и

${ Displaystyle omega = 2 пи е ,}$ куда

${ displaystyle omega ,}$ это угловая частота в радианы на второй (рад / с)

${ displaystyle f ,}$ это частота в герц (Гц)

${ Displaystyle т ,}$ время в секундах (с)

${ Displaystyle А ,}$ и ${ Displaystyle B ,}$ находятся константы

${ displaystyle ell ,}$ расстояние, измеренное вдоль линии передачи от нагрузки до генератора в метрах (м)

Также

${ Displaystyle гамма = альфа + J бета ,}$ это постоянная распространения который имеет единицы 1 / м

куда

${ Displaystyle альфа ,}$ это постоянная затухания в неперс на метр (Нп / м)

${ Displaystyle бета ,}$ это фазовая постоянная в радианы на метр (рад / м)

Диаграмма Смита используется с одной частотой (${ displaystyle omega}$) за раз, и только на один момент (${ displaystyle t}$) за один раз, поэтому временная часть фазы (${ Displaystyle ехр (J омега т) ,}$) фиксированный. Фактически все члены умножаются на это, чтобы получить мгновенная фаза, но это общепринято и принято опускать его. Следовательно,

${ Displaystyle В _ { текст {F}} = А ехр (+ гамма ell) ,}$ и

${ Displaystyle В _ { текст {R}} = В ехр (- гамма ell) ,}$

куда ${ Displaystyle А ,}$ и ${ Displaystyle B ,}$ - соответственно амплитуды прямого и обратного напряжения на нагрузке.

Изменение комплексного коэффициента отражения в зависимости от положения вдоль линии

Глядя на груз по длине ${ displaystyle ell ,}$ линии передачи без потерь импеданс изменяется как ${ displaystyle ell ,}$ увеличивается, следуя синему кругу. (Этот импеданс характеризуется коэффициентом отражения ${ Displaystyle V _ { text {отраженный}} / V _ { text {инцидент}}}$.) Синий кружок с центром на диаграмме Смита импеданса иногда называют КСВ круг (Короче для постоянный коэффициент стоячей волны ).

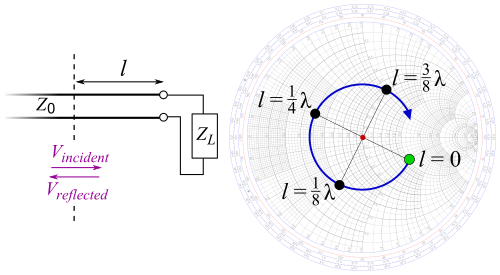
Комплексный коэффициент отражения напряжения ${ displaystyle Gamma ,}$ определяется как отношение отраженной волны к падающей (или прямой) волне. Следовательно,

${ Displaystyle Gamma = { frac {V _ { text {R}}} {V _ { text {F}}}} = { frac {B exp (- gamma ell)} {A exp (+ gamma ell)}} = C exp (-2 gamma ell) ,}$

куда C также является константой.

Для единой ЛЭП (в которой ${ displaystyle gamma ,}$ постоянна), комплексный коэффициент отражения стоячей волны меняется в зависимости от положения на линии. Если линия с потерями (${ Displaystyle альфа ,}$ не равно нулю) это представлено на диаграмме Смита спираль дорожка. Однако в большинстве задач с диаграммой Смита потери можно считать незначительными (${ Displaystyle альфа = 0 ,}$) и задача их решения значительно упрощается. Поэтому для случая без потерь выражение для комплексного коэффициента отражения принимает вид

${ Displaystyle Gamma = Gamma _ { text {L}} exp (-2j beta ell) ,}$

куда ${ displaystyle Gamma _ { text {L}} ,}$ - коэффициент отражения от нагрузки, а ${ displaystyle ell ,}$ - длина линии от нагрузки до места измерения коэффициента отражения. Фазовая постоянная ${ Displaystyle бета ,}$ можно также записать как

${ Displaystyle бета = { гидроразрыва {2 pi} { lambda}} ,}$

куда ${ displaystyle lambda ,}$ это длина волны внутри линии передачи на тестовой частоте.

Следовательно,

${ displaystyle Gamma = Gamma _ { text {L}} exp left ({ frac {-4j pi} { lambda}} ell right) ,}$

Это уравнение показывает, что для стоячей волны комплексный коэффициент отражения и импеданс повторяются на каждой половине длины волны вдоль линии передачи. Комплексный коэффициент отражения обычно называют просто коэффициентом отражения. Внешняя круговая шкала диаграммы Смита представляет расстояние от генератора до нагрузки, масштабированное в длинах волн, и поэтому масштабируется от нуля до 0,50.

Изменение нормированного импеданса в зависимости от положения вдоль линии

Если ${ Displaystyle V ,}$ и ${ Displaystyle I ,}$ - напряжение и ток, поступающий на оконечную нагрузку в конце линии передачи, соответственно, тогда

${ Displaystyle V _ { текст {F}} + V _ { text {R}} = V ,}$ и

${ displaystyle V _ { text {F}} - V _ { text {R}} = Z_ {0} I ,}$.

Разделив эти уравнения и подставив оба коэффициента отражения напряжения

${ displaystyle Gamma = { frac {V _ { text {R}}} {V _ { text {F}}}} ,}$

и нормализованный импеданс завершения, представленный строчными буквами z, индекс T

${ displaystyle z _ { text {T}} = { frac {V} {Z_ {0} I}} ,}$

дает результат:

${ displaystyle z _ { text {T}} = { frac {1+ Gamma} {1- Gamma}} ,}$.

В качестве альтернативы по коэффициенту отражения

${ displaystyle Gamma = { frac {z _ { text {T}} - 1} {z _ { text {T}} + 1}} ,}$

Это уравнения, которые используются для построения Z Диаграмма Смита. Математически говоря ${ displaystyle Gamma ,}$ и ${ Displaystyle г _ { текст {T}} ,}$ связаны через Преобразование Мёбиуса.

Обе ${ displaystyle Gamma ,}$ и ${ Displaystyle г _ { текст {T}} ,}$ выражаются в сложные числа без каких-либо единиц. Они оба изменяются с частотой, поэтому для любого конкретного измерения частота, на которой оно проводилось, должна быть указана вместе с характеристическим сопротивлением.

${ displaystyle Gamma ,}$ может быть выражено в величина и угол на полярная диаграмма. Любой фактический коэффициент отражения должен иметь величину меньше или равную единство Таким образом, на тестовой частоте это может быть выражено точкой внутри круга с радиусом единицы. Диаграмма Смита фактически построена на такой полярной диаграмме. Масштабирование диаграммы Смита спроектировано таким образом, что коэффициент отражения можно преобразовать в нормализованный импеданс или наоборот. Используя диаграмму Смита, нормированный импеданс может быть получен с заметной точностью путем нанесения точки, представляющей коэффициент отражения рассмотрение диаграммы Смита как полярной диаграммы а затем считывание его значения напрямую с помощью масштабирования диаграммы Смита. Этот метод является графической альтернативой подстановке значений в уравнения.

Подставляя выражение для изменения коэффициента отражения вдоль несогласованной линии передачи без потерь

${ displaystyle Gamma = { frac {B exp (- gamma ell)} {A exp ( gamma ell)}} = { frac {B exp (-j beta ell)} {A exp (j beta ell)}} ,}$

для случая без потерь в уравнение для нормированного импеданса через коэффициент отражения

${ displaystyle z _ { text {T}} = { frac {1+ Gamma} {1- Gamma}} ,}$.

и используя Формула Эйлера

${ Displaystyle ехр (J тета) = соз тета + J грех тета ,}$

дает уравнение линии передачи импедансной версии для случая без потерь:^[10]

${ displaystyle Z _ { text {in}} = Z_ {0} { frac {Z _ { text {L}} + jZ_ {0} tan ( beta ell)} {Z_ {0} + jZ_ { text {L}} tan ( beta ell)}} ,}$

куда${ Displaystyle Z _ { текст {in}} ,}$ это импеданс, "видимый" на входе линии передачи без потерь длиной ${ displaystyle ell}$, оканчивающийся импедансом ${ Displaystyle Z _ { текст {L}} ,}$

Аналогичным образом могут быть получены версии уравнения линии передачи для случая без потерь полной проводимости и для случаев с потерями полного сопротивления и проводимости.

Графический эквивалент диаграммы Смита использования уравнения линии передачи - нормализация ${ Displaystyle Z _ { текст {L}} ,}$, чтобы нанести полученную точку на Z Диаграмма Смита и начертите круг через эту точку с центром в центре диаграммы Смита. Путь по дуге окружности показывает, как изменяется импеданс при движении по линии передачи. В этом случае необходимо использовать масштабирование по окружности (по длине волны), помня, что это длина волны в линии передачи, которая может отличаться от длины волны в свободном пространстве.

Регионы Z Диаграмма Смита

Если полярная диаграмма отображается на декартова система координат принято измерять углы относительно положительного Иксось с использованием против часовой стрелки направление для положительных углов. Величина комплексного числа - это длина прямой линии, проведенной от источник в точку, представляющую его. В диаграмме Смита используется то же соглашение, при этом отмечается, что в нормализованной плоскости импеданса положительная ось x проходит от центра диаграммы Смита на ${ displaystyle z _ { text {T}} = 1 pm j0 ,}$ к точке ${ Displaystyle г _ { текст {T}} = infty pm j infty ,}$. Область над осью абсцисс представляет индуктивные сопротивления (положительные мнимые части), а область ниже Икс- ось представляет собой емкостные сопротивления (отрицательные мнимые части).

Если окончание идеально совмещено, коэффициент отражения будет равен нулю, что фактически будет представлено кружком нулевого радиуса или фактически точкой в ​​центре диаграммы Смита. Если оконечная нагрузка была полностью разомкнутой, или короткое замыкание величина коэффициента отражения будет равна единице, вся мощность будет отражаться, и точка будет лежать в некоторой точке на окружности единичной окружности.

Круги постоянного нормированного сопротивления и постоянного нормированного реактивного сопротивления

Диаграмма Смита с нормализованным сопротивлением состоит из двух семейств кругов: кругов постоянного нормированного сопротивления и кругов постоянного нормированного реактивного сопротивления. В плоскости комплексных коэффициентов отражения диаграмма Смита занимает круг единичного радиуса с центром в начале координат. Поэтому в декартовых координатах круг будет проходить через точки (+1,0) и (−1,0) на Икс-оси и точки (0, + 1) и (0, −1) на у-ось.

Поскольку оба ${ displaystyle Gamma}$ и ${ Displaystyle г ,}$ являются комплексными числами, в общем случае они могут быть записаны как:

${ Displaystyle г = а + jb ,}$

${ displaystyle Gamma = c + jd ,}$

с а, б, c и d действительные числа.

Подставив их в уравнение, связывающее нормализованный импеданс и комплексный коэффициент отражения:

${ Displaystyle Gamma = { гидроразрыва {z-1} {z + 1}} ,}$

дает следующий результат:

${ displaystyle Gamma = c + jd = left [{ frac {a ^ {2} + b ^ {2} -1} {(a + 1) ^ {2} + b ^ {2}}} right] + j left [{ frac {2b} {(a + 1) ^ {2} + b ^ {2}}} right] ,}$.

Это уравнение, которое описывает, как комплексный коэффициент отражения изменяется с нормализованным импедансом, и может использоваться для построения обоих семейств кругов.^[11]

В Y Диаграмма Смита

В Y Диаграмма Смита строится аналогично диаграмме Смита. Z Случай диаграммы Смита, но путем выражения значений коэффициента отражения напряжения в терминах нормализованной проводимости вместо нормализованного импеданса. Нормализованный допуск у_Т является обратной величиной нормализованного импеданса z_Т, так

${ displaystyle y _ { text {T}} = { frac {1} {z _ { text {T}}}} ,}$

Следовательно:

${ displaystyle y _ { text {T}} = { frac {1- Gamma} {1+ Gamma}} ,}$

и

${ displaystyle Gamma = { frac {1-y _ { text {T}}} {1 + y _ { text {T}}}} ,}$

В Y Диаграмма Смита выглядит как нормализованный тип импеданса, но с графическим масштабированием, повернутым на 180 °, числовое масштабирование остается неизменным.

Область выше Икс- ось представляет собой емкостные проводимости, а область ниже Икс- ось представляет собой индуктивные допуски. Емкостные допуски имеют положительный воображаемый части и индуктивные допуски имеют отрицательные мнимые части.

Опять же, если окончание идеально согласовано, коэффициент отражения будет равен нулю, что будет представлено «кружком» нулевого радиуса или фактически точкой в ​​центре диаграммы Смита. Если завершение было полностью разомкнутым или коротким замыканием, величина коэффициента отражения напряжения была бы единицей, вся мощность отражалась бы, и точка лежала бы в некоторой точке на окружности единичной окружности диаграммы Смита.

Практические примеры

Примеры точек на диаграмме Смита с нормализованным импедансом

Точка с коэффициентом отражения 0,63 и углом 60 °, представленная в полярной форме как ${ Displaystyle 0,63 угол 60 ^ { circ} ,}$, обозначена точкой P₁ на диаграмме Смита. Для построения графика можно использовать круговую шкалу углов (коэффициента отражения), чтобы найти ${ Displaystyle angle 60 ^ { circ} ,}$ градуировку и линейку, чтобы провести линию, проходящую через это и в центр диаграммы Смита. Длина линии тогда будет масштабирована до P₁ в предположении, что радиус диаграммы Смита равен единице. Например, если фактический радиус, измеренный от бумаги, составлял 100 мм, длина OP₁ будет 63 мм.

В следующей таблице приведены некоторые похожие примеры точек, нанесенных на Z Диаграмма Смита. Для каждого коэффициент отражения дан в полярной форме вместе с соответствующим нормированным импедансом в прямоугольной форме. Преобразование можно прочитать непосредственно из диаграммы Смита или путем подстановки в уравнение.

Некоторые примеры точек, нанесенных на диаграмму Смита с нормализованным импедансом

Идентификация точки	Коэффициент отражения (полярная форма)	Нормализованный импеданс (прямоугольная форма)
п1 (Индуктивный)	${ Displaystyle 0,63 угол 60 ^ { circ} ,}$	${ displaystyle 0.80 + j1.40 ,}$
п2 (Индуктивный)	${ Displaystyle 0,73 угол 125 ^ { circ} ,}$	${ displaystyle 0.20 + j0.50 ,}$
п3 (Емкостный)	${ Displaystyle 0,44 угол -116 ^ { circ} ,}$	${ displaystyle 0.50-j0.50 ,}$

Работая как с Z Диаграмма Смита и Y Диаграммы Смита

В ВЧ схемах и задачах согласования иногда удобнее работать с допусками (представляющими проводимость и подозрения ), а иногда удобнее работать с импедансами (представляющими сопротивления и реактивные сопротивления ). Решение типичной проблемы согласования часто требует нескольких изменений между обоими типами диаграммы Смита с использованием нормализованного импеданса для серии элементы и нормированные допуски для параллельно элементы. Для этого можно использовать диаграмму Смита с двойным (нормализованным) импедансом и проводимостью. В качестве альтернативы можно использовать один тип и при необходимости преобразовать масштабирование в другой. Чтобы перейти от нормализованного импеданса к нормализованной проводимости или наоборот, точка, представляющая значение рассматриваемого коэффициента отражения, перемещается точно на 180 градусов с тем же радиусом. Например, точка P1 в примере, представляющая коэффициент отражения ${ Displaystyle 0,63 угол 60 ^ { circ} ,}$ имеет нормализованный импеданс ${ Displaystyle Z_ {P} = 0.80 + j1.40 ,}$. Чтобы графически изменить это на эквивалентную точку нормализованной проводимости, скажем Q1, линейкой проводится линия от P1 через центр диаграммы Смита к Q1, равный радиус в противоположном направлении. Это эквивалентно перемещению точки по круговой траектории ровно на 180 градусов. Чтение значения из диаграммы Смита для Q1, помня, что масштабирование теперь в нормированном допуске, дает ${ Displaystyle y_ {P} = 0,30-j0,54 ,}$. Выполнение расчета

${ displaystyle y _ { text {T}} = { frac {1} {z _ { text {T}}}} ,}$

вручную подтвердит это.

Когда трансформация При переходе от импеданса к полной проводимости масштабирование изменяется на нормализованную проводимость до тех пор, пока не будет выполнено более позднее преобразование обратно в нормализованное сопротивление.

В таблице ниже приведены примеры нормированных импедансов и их эквивалентных нормированных проводимостей, полученных поворотом точки на 180 °. Опять же, их можно получить либо путем расчета, либо с использованием диаграммы Смита, как показано, путем преобразования между плоскостями нормализованного импеданса и нормализованной проводимости.

Значения коэффициента отражения как нормированные импедансы и эквивалентные нормированные проводимости

Плоскость нормализованного импеданса	Плоскость нормализованной проводимости
п1 (${ Displaystyle Z = 0,80 + j1,40 ,}$)	Q1 (${ Displaystyle у = 0,30-j0,54 ,}$)
п10 (${ Displaystyle Z = 0,10 + j0,22 ,}$)	Q10 (${ displaystyle y = 1,80-j3,90 ,}$)

Значения комплексного коэффициента отражения, нанесенные на диаграмму Смита с нормализованным импедансом, и их эквиваленты на диаграмме Смита с нормализованной проводимостью

Выбор типа диаграммы Смита и типа компонента

Выбор использования Z Диаграмма Смита или Y Диаграмма Смита для любого конкретного расчета зависит от того, что удобнее. Последовательные и параллельные импедансы складываются, в то время как импедансы параллельно и проводимости связаны обратным уравнением. Если ${ displaystyle Z _ { text {TS}}}$ эквивалентный импеданс последовательного импеданса и ${ displaystyle Z _ { text {TP}}}$ эквивалентный импеданс параллельных импедансов, тогда

${ Displaystyle Z _ { текст {TS}} = Z_ {1} + Z_ {2} + Z_ {3} + ... ,}$

${ displaystyle { frac {1} {Z _ { text {TP}}}} = { frac {1} {Z_ {1}}} + { frac {1} {Z_ {2}}} + { frac {1} {Z_ {3}}} + ... ,}$

Для допусков верно обратное, то есть

${ displaystyle Y _ { text {TP}} = Y_ {1} + Y_ {2} + Y_ {3} + ... ,}$

${ displaystyle { frac {1} {Y _ { text {TS}}}} = { frac {1} {Y_ {1}}} + { frac {1} {Y_ {2}}} + { frac {1} {Y_ {3}}} + ... ,}$

Работа с взаимные, особенно в комплексных числах, требует больше времени и подвержен ошибкам, чем использование линейного сложения. Поэтому в целом большинство РФ инженеры работают в самолете, где топография схемы поддерживает линейное сложение. В следующей таблице приведены сложные выражения для импеданса (действительного и нормализованного) и проводимости (действительного и нормализованного) для каждого из трех основных пассивные элементы схемы: сопротивление, индуктивность и емкость. Используя только характеристическое сопротивление (или характеристическую проводимость) и испытательную частоту, эквивалентная схема можно найти и наоборот.

Выражения для импеданса и адмиттанса
Нормализовано по импедансу Z₀ или допуск Y₀

Тип элемента	Импеданс (Z или же z) или реактивность (Икс или же Икс)		Прием (Y или же у) или приостановление (B или же б)
	Настоящий (${ displaystyle Omega ,}$)	Нормализованный (без единицы измерения)	Реальный (S)	Нормализованный (без единицы измерения)
Сопротивление (р)	${ Displaystyle Z = R ,}$	${ displaystyle z = { frac {R} {Z_ {0}}} = RY_ {0} ,}$	${ displaystyle Y = G = { frac {1} {R}} ,}$	${ displaystyle y = g = { frac {1} {RY_ {0}}} = { frac {Z_ {0}} {R}} ,}$
Индуктивность (L)	${ Displaystyle Z = jX _ { текст {L}} = j omega L ,}$	${ displaystyle z = jx _ { text {L}} = j { frac { omega L} {Z_ {0}}} = j omega LY_ {0} ,}$	${ displaystyle Y = -jB _ { text {L}} = { frac {-j} { omega L}}}$	${ displaystyle y = -jb _ { text {L}} = { frac {-j} { omega LY_ {0}}} = { frac {-jZ_ {0}} { omega L}} , }$
Емкость (C)	${ displaystyle Z = -jX _ { text {C}} = { frac {-j} { omega C}} ,}$	${ displaystyle z = -jx _ { text {C}} = { frac {-j} { omega CZ_ {0}}} = { frac {-jY_ {0}} { omega C}} , }$	${ displaystyle Y = jB _ { text {C}} = j omega C ,}$	${ displaystyle y = jb _ { text {C}} = j { frac { omega C} {Y_ {0}}} = j omega CZ_ {0} ,}$

Использование диаграммы Смита для решения задач сопряженного сопоставления с распределенными компонентами

Распределенное согласование становится возможным и иногда требуется, когда физический размер согласующих компонентов составляет более примерно 5% длины волны на рабочей частоте. Здесь электрическое поведение многих сосредоточенных компонентов становится довольно непредсказуемым. Это происходит в микроволновых цепях и когда для высокой мощности требуются большие компоненты в коротковолновом, FM- и ТВ-вещании,

Для распределенных компонентов влияние на коэффициент отражения и импеданс движения вдоль линии передачи должно быть учтено для использования внешней круговой шкалы диаграммы Смита, которая откалибрована по длинам волн.

В следующем примере показано, как линия передачи, оканчивающаяся произвольной нагрузкой, может быть согласована на одной частоте с последовательным или параллельным реактивным компонентом, в каждом случае подключенным в определенных местах.

Построение диаграммы Смита для согласования некоторых распределенных линий передачи

Предположим, что линия передачи без потерь с разнесением по воздуху с характеристическим сопротивлением ${ Displaystyle Z_ {0} = 50 Omega}$, работающий на частоте 800 МГц, оканчивается цепью, содержащей 17,5 ${ displaystyle Omega}$ резистор, включенный последовательно с катушкой индуктивности 6,5 наногенри (6,5 нГн). Как можно сопоставить линию?

Из приведенной выше таблицы реактивное сопротивление катушки индуктивности, составляющей часть согласования, на частоте 800 МГц составляет

${ Displaystyle Z_ {L} = j omega L = j2 pi fL = j32.7 Omega ,}$

так что сопротивление комбинации (${ displaystyle Z_ {T}}$) дан кем-то

${ Displaystyle Z_ {T} = 17,5 + j32,7 Omega ,}$

и нормализованный импеданс (${ displaystyle z_ {T}}$) является

${ displaystyle z_ {T} = { frac {Z_ {T}} {Z_ {0}}} = 0,35 + j0,65 ,}$

Это отображается на диаграмме Z Смита в точке P₂₀. Линия OP₂₀ расширяется до шкалы длин волн, где она пересекается в точке ${ Displaystyle L_ {1} = 0,098 лямбда ,}$. Поскольку в линии передачи отсутствуют потери, через точку P проведен круг с центром в центре диаграммы Смита.₂₀ для представления пути коэффициента отражения с постоянной величиной из-за прекращения. В точке P₂₁ круг пересекается с единичным кругом постоянного нормированного сопротивления при

${ displaystyle z_ {P21} = 1,00 + j1,52 ,}$.

Продолжение линии OP₂₁ пересекает шкалу длин волн на ${ Displaystyle L_ {2} = 0,177 лямбда ,}$, поэтому расстояние от окончания до этой точки на линии определяется выражением

${ Displaystyle L_ {2} -L_ {1} = 0,177 лямбда -0,098 лямбда = 0,079 лямбда ,}$

Поскольку линия передачи разнесена по воздуху, длина волны 800 МГц в линии такая же, как и в свободном пространстве, и определяется выражением

${ displaystyle lambda = { frac {c} {f}} ,}$

куда ${ displaystyle c ,}$ это скорость электромагнитное излучение в свободном пространстве и ${ displaystyle f ,}$ - частота в герцах. Результат дает ${ Displaystyle lambda = 375 mathrm {мм} ,}$, делая положение согласующего компонента 29,6 мм от груза.

Сопряженное соответствие для импеданса в P₂₁ (${ displaystyle z_ {match} ,}$) является

${ displaystyle z_ {match} = - j (1.52), !}$

Поскольку диаграмма Смита все еще находится в плоскости нормализованного импеданса, из таблицы выше последовательный конденсатор ${ Displaystyle C_ {m} ,}$ требуется там, где

${ displaystyle z_ {match} = - j1.52 = { frac {-j} { omega C_ {m} Z_ {0}}} = { frac {-j} {2 pi fC_ {m} Z_ {0}}} ,}$

Переставляя, получаем

${ displaystyle C_ {m} = { frac {1} {(1.52) omega Z_ {0}}} = { frac {1} {(1.52) (2 pi f) Z_ {0}}}}$.

Подстановка известных значений дает

${ Displaystyle C_ {m} = 2,6 mathrm {pF} ,}$

Чтобы согласовать оконечную нагрузку на частоте 800 МГц, последовательный конденсатор 2,6 пФ должен быть включен последовательно с линией передачи на расстоянии 29,6 мм от оконечной нагрузки.

Альтернативное согласование шунта можно рассчитать после выполнения преобразования диаграммы Смита из нормализованного импеданса в нормализованную проводимость. Точка Q₂₀ эквивалентен P₂₀ но выражается как нормализованный допуск. Считывая масштаб диаграммы Смита, помня, что теперь это нормализованный допуск,

${ displaystyle y_ {Q20} = 0,65-j1,20 ,}$

(Фактически это значение фактически не используется). Однако продолжение линии OQ₂₀ до шкалы длин волн дает ${ Displaystyle L_ {3} = 0,152 лямбда ,}$. Самая ранняя точка, в которой может быть введено сопряженное согласование шунта, двигаясь к генератору, будет в Q₂₁, то же положение, что и предыдущий P₂₁, но на этот раз представляет собой нормированный допуск, задаваемый

${ displaystyle y_ {Q21} = 1,00 + j1,52 ,}$.

Расстояние по линии передачи в этом случае

${ Displaystyle L_ {2} + L_ {3} = 0,177 лямбда +0,152 лямбда = 0,329 лямбда ,}$

что преобразуется в 123 мм.

Компонент сопряженного согласования должен иметь нормализованную проводимость (${ displaystyle y_ {совпадение}}$) из

${ displaystyle y_ {match} = - j1.52 ,}$.

Из таблицы видно, что для отрицательной полной проводимости потребуется индуктор, подключенный параллельно линии передачи. Если его значение ${ displaystyle L_ {m} ,}$, тогда

${ displaystyle -j1.52 = { frac {-j} { omega L_ {m} Y_ {0}}} = { frac {-jZ_ {0}} {2 pi fL_ {m}}} ,}$

Это дает результат

${ Displaystyle L_ {м} = 6.5 mathrm {nH} ,}$

Следовательно, подходящим индуктивным шунтирующим согласованием будет катушка индуктивности 6,5 нГн, включенная параллельно линии, расположенной на расстоянии 123 мм от нагрузки.

Использование диаграммы Смита для анализа цепей с сосредоточенными элементами

Анализ сосредоточенный элемент Компоненты предполагает, что длина волны на рабочей частоте намного больше, чем размеры самих компонентов. Диаграмма Смита может использоваться для анализа таких цепей, и в этом случае перемещения по диаграмме генерируются (нормализованными) импедансами и проводимостью компонентов при рабочей частоте. В этом случае масштабирование длины волны по окружности диаграммы Смита не используется. Следующая схема будет проанализирована с использованием диаграммы Смита на рабочей частоте 100 МГц. На этой частоте длина волны в свободном пространстве составляет 3 м. Сами размеры компонентов будут порядка миллиметров, поэтому предположение о сосредоточенных компонентах будет справедливым. Несмотря на отсутствие линии передачи как таковой, необходимо определить полное сопротивление системы, чтобы можно было проводить расчеты нормализации и денормализации и ${ Displaystyle Z_ {0} = 50 Omega ,}$ здесь хороший выбор, так как ${ Displaystyle R_ {1} = 50 Omega ,}$. Если бы сопротивления были очень разными, то лучше было бы представить значение, близкое к ним.

Схема с сосредоточенными элементами, которую можно проанализировать с помощью диаграммы Смита.

Диаграмма Смита с графическим построением для анализа контуров с сосредоточенными параметрами

Анализ начинается с диаграммы Z Смита, изучающей R₁ только без других компонентов. В качестве ${ Displaystyle R_ {1} = 50 Omega ,}$ то же самое, что и полное сопротивление системы, оно представлено точкой в ​​центре диаграммы Смита. Первое преобразование - OP₁ вдоль линии постоянного нормированного сопротивления в этом случае добавление нормализованного реактивного сопротивления -j0,80, что соответствует последовательному конденсатору на 40 пФ. Точки с суффиксом P находятся в Z плоскости и точки с суффиксом Q находятся в Y самолет. Следовательно, преобразования п₁ к Q₁ и п₃ к Q₃ от диаграммы Z Смита к диаграмме Смита Y и преобразованию Q₂ к п₂ находится от диаграммы Y Смита к диаграмме Z Смита. В следующей таблице показаны шаги, предпринятые для проработки оставшихся компонентов и преобразований, возвращение в конечном итоге обратно в центр диаграммы Смита и идеальное совпадение 50 Ом.

Шаги диаграммы Смита для анализа схемы с сосредоточенными элементами

Трансформация	Самолет	Икс или же у Нормализованное значение	Емкость / Индуктивность	Формула для решения	Результат
${ Displaystyle О rightarrow P_ {1} ,}$	${ Displaystyle Z ,}$	${ displaystyle -j0.80 ,}$	Емкость (серия)	${ displaystyle -j0.80 = { frac {-j} { omega C_ {1} Z_ {0}}} ,}$	${ Displaystyle C_ {1} = 40 mathrm {pF} ,}$
${ Displaystyle Q_ {1} rightarrow Q_ {2} ,}$	${ Displaystyle Y ,}$	${ displaystyle -j1.49 ,}$	Индуктивность (шунт)	${ displaystyle -j1.49 = { frac {-j} { omega L_ {1} Y_ {0}}} ,}$	${ Displaystyle L_ {1} = 53 mathrm {nH} ,}$
${ Displaystyle P_ {2} rightarrow P_ {3} ,}$	Z	${ displaystyle -j0.23 ,}$	Емкость (серия)	${ displaystyle -j0.23 = { frac {-j} { omega C_ {2} Z_ {0}}} ,}$	${ Displaystyle C_ {2} = 138 mathrm {pF} ,}$
${ Displaystyle Q_ {3} rightarrow O ,}$	Y	${ displaystyle + j1.14 ,}$	Емкость (шунт)	${ displaystyle + j1.14 = { frac {j omega C_ {3}} {Y_ {0}}} ,}$	${ Displaystyle C_ {3} = 36 mathrm {pF} ,}$

Трехмерная диаграмма Смита

Трехмерное представление диаграммы Смита

Обобщенная трехмерная диаграмма Смита на основе расширенной комплексной плоскости (Сфера Римана ) и инверсивная геометрия был предложен в 2011 году. Схема объединяет пассивную и активную схему проектирования на малых и больших кругах на поверхности единичной сферы с использованием стереографической конформная карта обобщенной плоскости коэффициента отражения. Учитывая точку на бесконечности, пространство нового графика включает в себя все возможные нагрузки. Северный полюс - идеальная точка согласования, а южный полюс - идеальная точка несовпадения.^[12]

Рекомендации

дальнейшее чтение

• Для более раннего представления этого графического изображения до того, как они были названы «Диаграммы Смита», см. Кэмпбелл, Г.А. (1911). «Цизоидальные колебания». Труды Американского института инженеров-электриков. 30 (1–6): 789–824. Дои:10.1109 / PAIEE.1911.6659711., В частности, рис. 13 на стр. 810.

внешняя ссылка

• «Математическое построение и свойства диаграммы Смита». allaboutcircuits.com. технические статьи.
• «Учебное пособие по диаграмме Смита и согласованию импеданса с примерами». антенна-theory.com.
• "Диаграмма Мидзухаси-Смита". www.linkclub.or.jp/~morikuni. Архивировано из оригинал на 2013-03-03.
• "Диаграмма Смита Excel". excelhero.com. Август 2010 г. Некоммерческая интерактивная диаграмма Смита, которая лучше всего выглядит в Excel 2007+.
• "Инструмент 3D-диаграммы Смита". 3dsmithchart.com. (требуется Java) Некоммерческий универсальный инструмент для активных и пассивных схем.
• «СимСмит». ae6ty.com. Некоммерческий, доступен для Windows, Mac и Linux. Многие обучающие видео по диаграммам Смита. Нет ограничений по размеру схемы. Не ограничивается лестничными цепями.
• «Смит v3». fritz.dellsperger.net. Архивировано из оригинал на 2015-03-04. Коммерческая и бесплатная диаграмма Смита для Windows
• «КвикСмит». github.com/niyeradori. Бесплатный веб-инструмент для обучения диаграмм Смита доступен на GitHub.