Спин-бокал - Википедия - Spin glass

Было высказано предположение, что Переход Гарднера быть слился в эту статью. (Обсуждать) Предлагается с июня 2020 года.

Схематическое изображение случайный спиновая структура спин-стекло (вверху) и упорядоченный один из ферромагнетик (Нижний)

Стекло (аморфный SiO₂)

Кварц (кристаллический SiO₂)

Магнитный беспорядок спинового стекла по сравнению с ферромагнетиком аналогичен позиционному беспорядку стекла (слева) по сравнению с кварцем (справа).

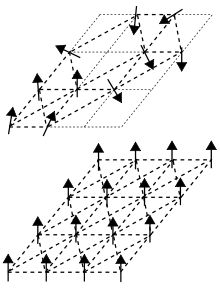
В физика конденсированного состояния, а спин-стекло модель определенного типа магнит. Магнитные спины - это, грубо говоря, ориентация северного и южного магнитных полюсов в трехмерном пространстве. В ферромагнитный твердые тела, составляющие атомы магнитные спины все выравниваются в одном направлении. Спиновые стекла контрастируют с ферромагнетиками как "беспорядочный «магниты, в которых спины их атомов не выровнены по правильному шаблону.

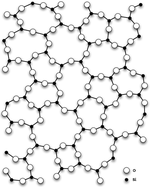
Термин «стекло» происходит от аналогии между магнитный беспорядок в спин-стакане и позиционный расстройство обычного, химического стекло, например, оконное стекло. В оконном стекле или любом другом аморфное твердое тело структура атомных связей сильно нерегулярна; в отличие от кристалл имеет однородный образец атомных связей. В ферромагнитный твердые тела, магнитные спины ориентированы в одном направлении; это аналогично кристаллу решетчатая структура.

Отдельные атомные связи в спиновом стекле представляют собой смесь примерно равного количества ферромагнитных связей (где соседи имеют одинаковую ориентацию) и антиферромагнитный связи (где соседи имеют прямо противоположную ориентацию: северный и южный полюса перевернуты на 180 градусов). Эти узоры выровненных и несовмещенных атомных магнитов создают то, что известно как неудовлетворенные взаимодействия - искажения геометрии атомных связей по сравнению с тем, что можно было бы увидеть в обычном, полностью выровненном твердом теле. Они также могут создавать ситуации, когда стабильно более чем одно геометрическое расположение атомов.

Спиновые стекла и возникающие в них сложные внутренние структуры называются "метастабильный "потому что они" застряли "в стабильных конфигурациях, отличных от конфигурация с наименьшим энергопотреблением (который был бы совмещенным и ферромагнитным). Математическую сложность этих структур сложно, но плодотворно исследовать экспериментально или в симуляции; с приложениями к физике, химии, материаловедению и искусственные нейронные сети в информатике.

Магнитное поведение

Именно временная зависимость отличает спиновые стекла от других магнитных систем.

Над стеклом температура перехода, Т_c,^{[примечание 1]} спиновое стекло демонстрирует типичные магнитные свойства (например, парамагнетизм ).

Если магнитное поле применяется при охлаждении образца до температуры перехода, намагниченность образца увеличивается, как описано Закон Кюри. По достижении Т_c, образец становится спиновым стеклом, и дальнейшее охлаждение приводит к небольшому изменению намагниченности. Это называется с полевым охлаждением намагниченность.

Когда внешнее магнитное поле удаляется, намагниченность спинового стекла быстро падает до более низкого значения, известного как остающийся намагниченность.

Затем намагниченность медленно спадает по мере приближения к нулю (или некоторой небольшой части исходного значения - это остается неизвестным ). Этот распад неэкспоненциальный и никакая простая функция не может адекватно соответствовать кривой намагничивания от времени.^[1] Этот медленный распад характерен для спиновых стекол. Экспериментальные измерения в течение нескольких дней показали постоянные изменения, превышающие уровень шума приборов.^[1]

Спиновые стекла отличаются от ферромагнетиков тем, что после снятия внешнего магнитного поля с ферромагнитного вещества намагниченность неопределенно долго остается на остаточном значении. Парамагнетики отличаются от спиновых стекол тем, что после снятия внешнего магнитного поля намагниченность быстро падает до нуля без остаточной намагниченности. Затухание быстрое и экспоненциальное.^{[нужна цитата ]}

Если образец охлаждается ниже Т_c в отсутствие внешнего магнитного поля и приложения магнитного поля после перехода в фазу спинового стекла происходит быстрое начальное увеличение до значения, называемого с нулевым охлаждением намагниченность. Затем происходит медленный дрейф вверх в сторону намагниченности, охлаждаемой полем.

Удивительно, но сумма двух сложных функций времени (охлаждение в нулевом поле и остаточная намагниченность) является постоянной величиной, а именно величиной, охлаждаемой полем, и, таким образом, обе имеют идентичные функциональные формы со временем,^[2] по крайней мере, в пределе очень малых внешних полей.

Модель Эдвардса – Андерсона

В этой модели спины расположены на ${ displaystyle d}$-мерная решетка с взаимодействиями только ближайших соседей, подобными Модель Изинга. Эта модель может быть решена точно для критических температур, и стеклообразная фаза наблюдается при низких температурах.^[3] В Гамильтониан для этой спиновой системы определяется как:

${ displaystyle H = - sum _ { langle ij rangle} J_ {ij} S_ {i} S_ {j},}$

куда ${ displaystyle S_ {i}}$ относится к Матрица спина Паули для частицы со спином в точке решетки ${ displaystyle i}$. Отрицательное значение ${ displaystyle J_ {ij}}$ обозначает взаимодействие антиферромагнитного типа между спинами в точках ${ displaystyle i}$ и ${ displaystyle j}$. Сумма проходит по всем ближайшим соседним позициям на решетке любой размерности. Переменные ${ displaystyle J_ {ij}}$ представляющие магнитную природу спин-спинового взаимодействия, называются связующими или звеньевыми переменными.

Чтобы определить статистическую сумму для этой системы, необходимо усреднить свободную энергию ${ displaystyle f left [J_ {ij} right] = - { frac {1} { beta}} ln { mathcal {Z}} left [J_ {ij} right]}$ куда ${ displaystyle { mathcal {Z}} left [J_ {ij} right] = operatorname {Tr} _ {S} left (e ^ {- beta H} right)}$, по всем возможным значениям ${ displaystyle J_ {ij}}$. Распределение значений ${ displaystyle J_ {ij}}$ рассматривается как гауссиан со средним ${ displaystyle J_ {0}}$ и отклонение ${ displaystyle J ^ {2}}$:

${ Displaystyle P (J_ {ij}) = { sqrt { frac {N} {2 pi J ^ {2}}}} exp left {- { frac {N} {2J ^ {2 }}} left (J_ {ij} - { frac {J_ {0}} {N}} right) ^ {2} right }.}$

Поиск свободной энергии с помощью метод реплики, ниже определенной температуры обнаруживается новая магнитная фаза, называемая фазой спинового стекла (или стеклообразной фазой) системы, которая характеризуется исчезающей намагниченностью ${ displaystyle m = 0}$ наряду с ненулевым значением двухточечной корреляционной функции между спинами в одной и той же точке решетки, но в двух разных репликах:

${ displaystyle q = sum _ {i = 1} ^ {N} S_ {i} ^ { alpha} S_ {i} ^ { beta} neq 0,}$

куда ${ displaystyle alpha, beta}$ индексы реплик. В параметр порядка для фазового перехода из ферромагнетика в спиновое стекло ${ displaystyle q}$, и что для парамагнетика для вращения стекла снова ${ displaystyle q}$. Следовательно, новый набор параметров порядка, описывающий три магнитные фазы, состоит из обоих ${ displaystyle m}$ и ${ displaystyle q}$.

В предположении симметрии реплики средняя свободная энергия поля определяется выражением:^[3]

${ displaystyle { begin {align} beta f = {} & - { frac { beta ^ {2} J ^ {2}} {4}} (1-q) ^ {2} + { frac { beta J_ {0} m ^ {2}} {2}} & - int exp left (- { frac {z ^ {2}} {2}} right) log left (2 cosh left ( beta Jz + beta J_ {0} m right) right) , mathrm {d} z. End {выравнивается}}}$

Модель Шеррингтона и Киркпатрика

Помимо необычных экспериментальных свойств, спиновые стекла являются предметом обширных теоретических и вычислительных исследований. Существенная часть ранних теоретических работ по спиновым стеклам касалась формы теория среднего поля на основе набора реплики из функция распределения системы.

Важная, точно решаемая модель спинового стекла была введена Дэвид Шеррингтон и Скотт Киркпатрик в 1975 году. Модель Изинга с ферро- и антиферромагнитными связями на больших расстояниях. Это соответствует приближение среднего поля спиновых стекол, описывающих медленную динамику намагниченности и сложное неэргодическое состояние равновесия.

В отличие от модели Эдвардса – Андерсона (EA), хотя в системе рассматриваются только двухспиновые взаимодействия, диапазон каждого взаимодействия потенциально может быть бесконечным (порядка размера решетки). Таким образом, мы видим, что любые два спина могут быть связаны ферромагнитной или антиферромагнитной связью, и их распределение дается точно так же, как в случае модели Эдвардса – Андерсона. Гамильтониан для модели SK очень похож на модель EA:

${ displaystyle H = - sum _ {я$

куда ${ displaystyle J_ {ij}, S_ {i}, S_ {j}}$ имеют то же значение, что и в модели советника. Равновесное решение модели после некоторых первоначальных попыток Шеррингтона, Киркпатрика и других было найдено Джорджио Паризи в 1979 г. методом реплик. Последующая работа по интерпретации решения Паризи - М. Мезаром, Ж. Паризи, М. А. Вирасоро и многими другими - выявила сложную природу стекловидной низкотемпературной фазы, характеризующейся нарушением эргодичности, ультраметричностью и несамоусредненностью. Дальнейшие разработки привели к созданию полостной метод, что позволило исследовать низкотемпературную фазу без реплик. Строгое доказательство решения Паризи было предоставлено в работе Франческо Герра и Мишель Талагранд.^[4]

Формализм теории среднего поля реплик также применялся при изучении нейронные сети, где он позволил вычислить такие свойства, как емкость памяти простых архитектур нейронных сетей, не требуя алгоритма обучения (например, обратное распространение ) должны быть разработаны или реализованы.^[5]

Более реалистичные модели спинового стекла с короткодействующими фрустрированными взаимодействиями и беспорядком, такие как Гауссовский модель, в которой связи между соседними спинами следуют Гауссово распределение, также были тщательно изучены, особенно с использованием Моделирование Монте-Карло. Эти модели отображают фазы спинового стекла, окаймленные острым фазовые переходы.

Помимо своей актуальности для физики конденсированного состояния, теория спинового стекла приобрела строго междисциплинарный характер с приложениями к нейронная сеть теория, информатика, теоретическая биология, эконофизика и Т. Д.

Модель с бесконечным диапазоном

Модель с бесконечным радиусом действия является обобщением Модель Шеррингтона – Киркпатрика где мы не только рассматриваем два спиновых взаимодействия, но и ${ displaystyle r}$-спиновые взаимодействия, где ${ displaystyle r leq N}$ и ${ displaystyle N}$ - общее количество вращений. В отличие от модели Эдвардса – Андерсона, аналогичной модели SK, диапазон взаимодействия по-прежнему бесконечен. Гамильтониан этой модели описывается следующим образом:

${ displaystyle H = - sum _ {i_ {1}$

куда ${ displaystyle J_ {i_ {1} dots i_ {r}}, S_ {i_ {1}}, dots, S_ {i_ {r}}}$ имеют те же значения, что и в модели советника. В ${ Displaystyle г к infty}$ предел этой модели известен как модель случайной энергии. В этом пределе можно видеть, что вероятность того, что спиновое стекло существует в определенном состоянии, зависит только от энергии этого состояния, а не от отдельных спиновых конфигураций в нем. Предполагается гауссово распределение магнитных связей по решетке обычно решать эту модель. Ожидается, что любое другое распределение даст такой же результат вследствие Центральная предельная теорема. Функция гауссова распределения со средним значением ${ displaystyle { frac {J_ {0}} {N}}}$ и дисперсия ${ displaystyle { frac {J ^ {2}} {N}}}$, определяется как:

${ displaystyle P left (J_ {i_ {1} cdots i_ {r}} right) = { sqrt { frac {N ^ {r-1}} {J ^ {2} pi r!} }} exp left {- { frac {N ^ {r-1}} {J ^ {2} r!}} left (J_ {i_ {1} cdots i_ {r}} - { гидроразрыв {J_ {0} r!} {2N ^ {r-1}}} right) right }}$

Параметры порядка для этой системы задаются намагниченностью ${ displaystyle m}$ и двухточечная спиновая корреляция между спинами в одном и том же месте ${ displaystyle q}$, в двух разных репликах, которые такие же, как у модели SK. Эта модель с бесконечным радиусом действия может быть явно решена для свободной энергии^[3] с точки зрения ${ displaystyle m}$ и ${ displaystyle q}$при условии симметрии реплики, а также нарушения симметрии 1-реплики.^[3]

${ displaystyle { begin {align} beta f = {} & { frac {1} {4}} beta ^ {2} J ^ {2} q ^ {r} - { frac {1} { 2}} r beta ^ {2} J ^ {2} q ^ {r} - { frac {1} {4}} beta ^ {2} J ^ {2} + { frac {1} { 2}} beta J_ {0} rm ^ {r} + { frac {1} {4 { sqrt {2 pi}}}} r beta ^ {2} J ^ {2} q ^ {r -1} + {} & int exp left (- { frac {1} {2}} z ^ {2} right) log left (2 cosh left ( beta Jz { sqrt {{ frac {1} {2}} rq ^ {r-1}}} + { frac {1} {2}} beta J_ {0} rm ^ {r-1} right) справа) , mathrm {d} z end {выровнено}}}$

Неэргодическое поведение и приложения

Термодинамическая система - это эргодический когда, учитывая любой (равновесный) экземпляр системы, она в конечном итоге посещает все другие возможные (равновесные) состояния (с той же энергией). Одной из характеристик систем спинового стекла является то, что ниже температуры замерзания ${ displaystyle T _ { text {f}}}$, экземпляры попадают в «неэргодический» набор состояний: система может колебаться между несколькими состояниями, но не может переходить в другие состояния с эквивалентной энергией. Интуитивно можно сказать, что система не может выйти из глубоких минимумов иерархически неупорядоченного энергетического ландшафта; расстояния между минимумами задаются ультраметрический, с высокими энергетическими барьерами между минимумами.^{[заметка 2]} В коэффициент участия подсчитывает количество состояний, доступных из данного экземпляра, то есть количество состояний, которые участвуют в основное состояние.

Для физических систем, таких как разбавленный марганец в меди, температура замерзания обычно составляет всего 30 ° C. кельвины (-240 ° C), и поэтому магнетизм спинового стекла практически не имеет применения в повседневной жизни. Однако неэргодические состояния и сложные энергетические ландшафты весьма полезны для понимания поведения определенных нейронные сети, включая Сети Хопфилда, а также множество проблем в Информатика оптимизация и генетика.

Самоиндуцированное спиновое стекло

В 2020 году ученые-физики из Radboud University и Уппсальский университет объявили, что наблюдали поведение, известное как самоиндуцированное спиновое стекло в атомной структуре неодима. Один из исследователей пояснил: «... мы специалисты в сканирующая туннельная микроскопия. Это позволяет нам видеть структуру отдельных атомов, и мы можем разрешить северный и южный полюса атомов. Благодаря этому прогрессу в области высокоточной визуализации мы смогли обнаружить поведение неодима, потому что мы смогли выявить невероятно малые изменения в магнитной структуре ». Неодим ведет себя сложным магнитным образом, который ранее не наблюдался в периодической таблице. элемент.^[6][7]

История отрасли

Подробный отчет об истории спиновых очков с начала 1960-х до конца 1980-х годов можно найти в серии популярных статей автора Филип В. Андерсон в Физика сегодня.^{[8][9][10][11][12][13][14]}

Смотрите также

Примечания

Рекомендации

Литература

• Edwards, S.F .; Андерсон, П.В. (1975), «Теория спиновых стекол», Журнал физики F: физика металлов, 5 (5): 965–974, Bibcode:1975JPhF .... 5..965E, Дои:10.1088/0305-4608/5/5/017. [1]
• Шеррингтон, Дэвид; Киркпатрик, Скотт (1975), "Решаемая модель спин-стекла", Письма с физическими проверками, 35 (26): 1792–1796, Bibcode:1975ПхРвЛ..35.1792С, Дои:10.1103 / PhysRevLett.35.1792. Резюме Papercore http://papercore.org/Sherrington1975
• Nordblad, P .; Lundgren, L .; Сандлунд, Л. (1986), "Связь между релаксацией охлажденного нулевого поля и термоостаточной намагниченностью в спиновых стеклах", Журнал магнетизма и магнитных материалов, 54: 185–186, Bibcode:1986JMMM ... 54..185N, Дои:10.1016/0304-8853(86)90543-3.
• Биндера, К.; Янг, А. П. (1986), "Спиновые очки: экспериментальные факты, теоретические концепции и открытые вопросы", Обзоры современной физики, 58 (4): 801–976, Bibcode:1986РвМП ... 58..801Б, Дои:10.1103 / RevModPhys.58.801.
• Bryngelson, Joseph D .; Уолинс, Питер Г. (1987), "Спиновые очки и статистическая механика сворачивания белков", Труды Национальной академии наук, 84 (21): 7524–7528, Bibcode:1987PNAS ... 84.7524B, Дои:10.1073 / пнас.84.21.7524, ЧВК  299331, PMID  3478708.
• Фишер, К. Х .; Герц, Дж. А. (1991), Спиновые очки, Издательство Кембриджского университета.
• Мезард, Марк; Паризи, Джорджио; Вирасоро, Мигель Анхель (1987), Теория спинового стекла и не только, Сингапур: World Scientific, ISBN  978-9971-5-0115-0.
• Майдош, Дж. А. (1995), Спиновые очки, Тейлор и Фрэнсис.
• Паризи, Г. (1980), «Параметр порядка для спиновых стекол: функция на интервале 0-1» (PDF), J. Phys. A: Математика. Gen., 13 (3): 1101–1112, Bibcode:1980JPhA ... 13.1101P, Дои:10.1088/0305-4470/13/3/042 Резюме Papercore http://papercore.org/Parisi1980.
• Талагранд, Мишель (2000), "Нарушение реплики симметрии и экспоненциальные неравенства для модели Шеррингтона – Киркпатрика", Анналы вероятности, 28 (3): 1018–1062, Дои:10.1214 / aop / 1019160325, JSTOR  2652978.
• .Guerra, F .; Тонинелли, Ф. Л. (2002), "Термодинамический предел в моделях спинового стекла среднего поля", Коммуникации по математической физике, 230 (1): 71–79, arXiv:cond-mat / 0204280, Bibcode:2002CMaPh.230 ... 71G, Дои:10.1007 / s00220-002-0699-у
• Аминов, Т. Г .; Новоторцев, В. Н. (2014), «Спиновые очки в Cu_0.5Fe_0.5Cr₂S₄ - Твердые растворы на основе », Неорганические материалы, 50 (13): 1343–00, Дои:10.1134 / s0020168514130020, ISSN  0020-1685

внешняя ссылка

• Краткое изложение основополагающей статьи Шеррингтона / Киркпатрика
• Статистика встречаемости термина "спин-стакан" на arxiv.org