Хронология вычисления π - Chronology of computation of π

Часть серия статей на
математическая константа π
3.1415926535897932384626433...
Использует
Свойства
Ценность
люди
История
В культуре
похожие темы

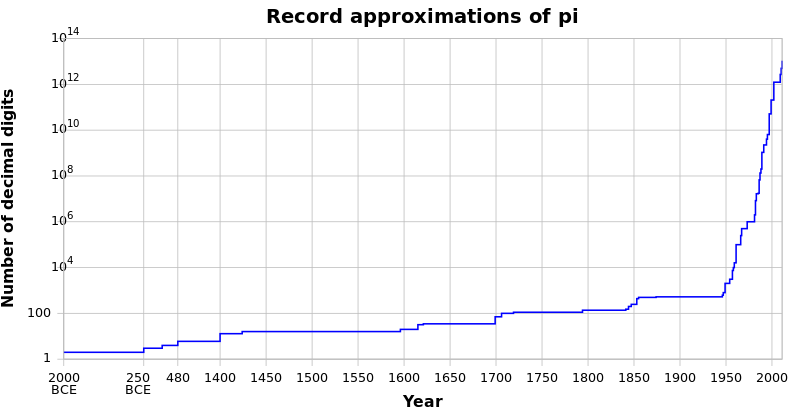
В таблице ниже представлена ​​краткая хронология вычисленных числовых значений или границ математической константы. Пи (π). Более подробные объяснения некоторых из этих расчетов см. Приближения π.

График, показывающий, как рекордная точность числовых приближений к Пи, измеряемых в десятичных разрядах (изображенных в логарифмической шкале), развивалась в истории человечества. Время до 1400 сжимается.

До 1400 г.

ДатаКтоОписание / использованный метод расчетаЦенностьДесятичные разряды
(мировые рекорды
в смелый)
2000? BCЕДревние египтяне[1]4 × (​8⁄9)23.1605...1
2000? BCЕДревние вавилоняне[1]3 + ​1⁄83.1251
1200? BCЕКитай[1]30
800–600 до н. Э.Шатапатха Брахмана (Санскрит: शतपथ ब्राह्मण) - 7.1.1.18 [2]Инструкция, как построить круглый алтарь из продолговатых кирпичей:

Он кладет на (круглую площадку) четыре (кирпича), идущих на восток 1; двое сзади идут крест-накрест (с юга на север), а двое (такие) впереди. Четыре, которых он надевает бегущими на восток, суть тела; а что касается их четырех, то это потому, что это тело (наше) состоит из четырех частей 2. Две сзади - это бедра; и двое впереди рук; и где тело (включает) голову ".[3]

(Санскрит: «स चतस्रः प्राचीरुपदधाति | द्वे पश्चात्तिरश्च्यौ द्वे पुरस्तात्तद्याश्चतस्रःप्राचीरुपदधाति भवन्ति चतुर्विधो ह्ययमात्माथ येपश्चात्ते सक्थ्यौ ये यत्र वा आत्मा तदेव शिरः»)

(Санскритская транслитерация: са катасрам працирупададхати | две пашчаттирашчйау двэ пурастаттадйашкатасраḥпрачирупадхати са атма тадйатташатасро бхаванти чатурвидхо хайаматмаутмаутха шатхатхашта йепатхата йепатхатхаштхата йепатха йепатхата)

​25⁄8 = 3.1251
800? BCЕСульбасутрас [4]

[5][6]

(​6⁄(2 + √2))23.088311 ...0
550? BCЕБиблия (3 Царств 7:23)[1]«... расплавленное море, десять локтей от одного края до другого: оно было кругом ... кругом его проходила линия в тридцать локтей»30
434 г. до н. Э.Анаксагор пытался квадрат круга[7]компас и линейкаАнаксагор не предлагал никакого решения0
c. 250 г. до н. Э.Архимед[1]​223⁄71 < π < ​22⁄73.140845... < π < 3.142857...2
15 г. до н. Э.Витрувий[5]​25⁄83.1251
от 1 до 5Лю Синь[5][8][9]Неизвестный метод определения числа Цзялян который подразумевает значение для π π ≈162⁄(√50+0.095)2.3.1547...1
130Чжан Хэн (Книга Поздней Хань )[1]√10 = 3.162277...
​736⁄232		3.1622...1
150Птолемей[1]​377⁄1203.141666...3
250Ван Фань[1]​142⁄453.155555...1
263Лю Хуэй[1]3.141024 < π < 3.142074
​3927⁄1250		3.14163
400Он Chengtian[5]​111035⁄353293.142885...2
480Цзу Чунчжи[1]3.1415926 < π < 3.1415927
3.14159267
499Арьябхата[1]​62832⁄200003.14164[10]
640Брахмагупта[1]√103.162277...1
800Аль-Хорезми[1]3.14164[10]
1150Бхаскара II[5]​3927⁄1250 и754⁄2403.14164[10]
1220Фибоначчи[1]3.1418183
1320Чжао Юцинь[5]3.1415926

1400–1949

ДатаКтоЗаметкаДесятичные разряды
(мировые рекорды в смелый)
Все записи, начиная с 1400, указаны как количество правильных десятичных знаков..
1400Мадхава СангамаграмыОбнаружил бесконечное степенной ряд расширение π,
теперь известный как Формула Лейбница для числа пи[11]		10
1424Джамшид аль-Каши[12]16
1573Валентин Отон​355⁄1136
1579Франсуа Виет[13]9
1593Адриан ван Румен[14]15
1596Людольф ван Сеулен20
161532
1621Виллеброрд Снелл (Снеллий)Ученик Ван Сеулена35
1630Кристоф Гринбергер[15][16]38
1665Исаак Ньютон[1]16
1681Такакадзу Секи[17]11
16
1699Авраам Шарп[1]Пи вычислено до 72 цифр, но не все верны71
1706Джон Мачин[1]100
1706Уильям ДжонсВведена греческая буква 'π '
1719Томас Фантэ де Ланьи[1]Вычислено 127 знаков после запятой, но не все верны112
1722Тошикиё Камата24
1722Катахиро Такебе41
1739Ёсисуке Мацунага51
1748Леонард ЭйлерИспользовала греческую букву 'π'в его книге Введение в Analysin Infinitorum и заверил свою популярность.
1761Иоганн Генрих ЛамбертДоказал, что π является иррациональный
1775ЭйлерУказал на возможность того, что π возможно трансцендентный
1789Юрий ВегаВычислено 143 десятичных знака, но не все верны126
1794Юрий Вега[1]Вычислено 140 знаков после запятой, но не все верны136
1794Адриан-Мари ЛежандрПоказало, что π² (и, следовательно, π) иррационально, и упомянул возможность того, что π может быть трансцендентным.
Конец 18 векаАнонимная рукописьОбнаружен в библиотеке Рэдклиффа в Оксфорде, Англия, обнаружен Ф. X. фон Заком и дает значение числа пи 154 цифрам, 152 из которых были правильными.152
1824Уильям Резерфорд[1]Вычислено 208 знаков после запятой, но не все верны152
1844Zacharias Dase и Страсницкий[1]Вычислено 205 знаков после запятой, но не все верны200
1847Томас Клаузен[1]Вычислено 250 знаков после запятой, но не все верны248
1853Lehmann[1]261
1853Резерфорд[1]440
1874Уильям Шанкс[1]На вычисление 707 десятичных знаков ушло 15 лет, но не все оказались верными (ошибку обнаружил Д. Фергюсон в 1946 году)527
1882Фердинанд фон ЛиндеманнДоказал, что π является трансцендентный (в Теорема Линдемана – Вейерштрасса )
1897Штат США ИндианаПриблизились к законодательному закреплению значения 3,2 (среди прочего) для π. Законопроект о доме № 246 принято единогласно. Законопроект приостановился в Сенате штата из-за предположения о возможных коммерческих мотивах, связанных с публикацией учебника.[18]1
1910Шриниваса РамануджанНайдено несколько быстро сходящихся бесконечных серий π, который может вычислить 8 знаков после запятой π с каждым термином в серии. С 1980-х годов его серия стала основой самых быстрых алгоритмов, используемых в настоящее время Yasumasa Kanada и Братья Чудновские вычислить π.
1946Д. Ф. ФергюсонНастольный калькулятор620
1947Иван НивенДал очень элементарное доказательство того, что π иррационально
Январь 1947 г.Д. Ф. ФергюсонНастольный калькулятор710
Сентябрь 1947 г.Д. Ф. ФергюсонНастольный калькулятор808
1949Леви Б. Смит и Джон РенчНастольный калькулятор1,120

С электронно-вычислительными машинами (1949–)

ДатаКтоРеализацияВремяДесятичные разряды
(мировые рекорды в смелый)
Все записи, начиная с 1949 г., были рассчитаны с помощью электронных компьютеров.
1949G. W. Reitwiesner et al.Первыми, кто использовал электронный компьютер ( ENIAC ) вычислять π [19]70 часов2,037
1953Курт МалерПоказало, что π это не Число Лиувилля
1954С. К. Николсон и Дж. ДжинелС использованием NORC [20]13 минут3,093
1957Джордж Э. ФелтонФерранти Компьютер Пегас (Лондон), подсчитано 10021 цифра, но не все верны[21]7,480
Январь 1958 г.Франсуа ЖенюIBM 704 [22]1,7 часов10,000
Май 1958 г.Джордж Э. ФелтонКомпьютер Pegasus (Лондон)33 часов10,021
1959Франсуа ЖенюIBM 704 (Париж)[23]4,3 часа16,167
1961Дэниел Шэнкс и Джон РенчIBM 7090 (Нью-Йорк)[24]8,7 часов100,265
1961Дж. М. ДжерардIBM 7090 (Лондон)39 минут20,000
1966Жан Гийо и Ж. ФиллиатрIBM 7030 (Париж)28 часов[неудачная проверка ]250,000
1967Жан Гийо и М. ДишамптCDC 6600 (Париж)28 часов500,000
1973Жан Гийо и Мартин БуйеCDC 760023,3 часов1,001,250
1981Кадзунори Миёси и Yasumasa KanadaFACOM M-2002,000,036
1981Жан ГийоНеизвестный2,000,050
1982Ёсиаки ТамураMELCOM 900II2,097,144
1982Ёсиаки Тамура и Yasumasa KanadaHITAC M-280H2,9 часа4,194,288
1982Ёсиаки Тамура и Yasumasa KanadaHITAC M-280H8,388,576
1983Yasumasa Kanada, Саяка Ёшино и Ёсиаки ТамураHITAC M-280H16,777,206
Октябрь 1983 г.Ясунори Уширо и Yasumasa KanadaHITAC S-810/2010,013,395
Октябрь 1985 г.Билл ГосперСимволика 367017,526,200
Январь 1986Дэвид Х. БейлиCRAY-229,360,111
Сентябрь 1986Yasumasa Kanada, Ёсиаки ТамураHITAC S-810/2033,554,414
Октябрь 1986Yasumasa Kanada, Ёсиаки ТамураHITAC S-810/2067,108,839
Январь 1987Yasumasa Kanada, Ёсиаки Тамура, Ёсинобу Кубо и другиеNEC SX-2134,214,700
Январь 1988 г.Yasumasa Kanada и Ёсиаки ТамураHITAC S-820/80201,326,551
Май 1989 г.Григорий В. Чудновский и Давид В. ЧудновскийCRAY-2 & IBM 3090 / VF480,000,000
Июнь 1989 г.Григорий В. Чудновский и Давид В. ЧудновскийIBM 3090535,339,270
Июль 1989 г.Yasumasa Kanada и Ёсиаки ТамураHITAC S-820/80536,870,898
Август 1989 г.Григорий В. Чудновский и Давид В. ЧудновскийIBM 30901,011,196,691
19 ноября 1989 г.Yasumasa Kanada и Ёсиаки ТамураHITAC S-820/801,073,740,799
Август 1991 г.Григорий В. Чудновский и Давид В. ЧудновскийСамодельный параллельный компьютер (подробности неизвестны, не проверено) [25]2,260,000,000
18 мая 1994Григорий В. Чудновский и Давид В. ЧудновскийНовый самодельный параллельный компьютер (подробности неизвестны, не проверено)4,044,000,000
26 июня 1995 г.Yasumasa Kanada и Дайсуке ТакахашиHITAC S-3800/480 (двойной процессор) [26]3,221,220,000
1995Саймон ПлаффНаходит формула что позволяет п-я шестнадцатеричная цифра числа Пи, вычисляемая без вычисления предыдущих цифр.
28 августа 1995 г.Yasumasa Kanada и Дайсуке ТакахашиHITAC S-3800/480 (двойной процессор) [27]4,294,960,000
11 октября 1995 г.Yasumasa Kanada и Дайсуке ТакахашиHITAC S-3800/480 (двойной процессор) [28]6,442,450,000
6 июля 1997 г.Yasumasa Kanada и Дайсуке ТакахашиHITACHI SR2201 (1024 ЦП) [29]51,539,600,000
5 апреля 1999 г.Yasumasa Kanada и Дайсуке ТакахашиHITACHI SR8000 (64 из 128 узлов) [30]68,719,470,000
20 сентября 1999 г.Yasumasa Kanada и Дайсуке ТакахашиHITACHI SR8000 / MPP (128 узлов) [31]206,158,430,000
24 ноября 2002 г.Yasumasa Kanada И команда из 9 человекHITACHI SR8000 / MPP (64 узла), Департамент информатики Токийский университет в Токио, Япония [32]600 часов1,241,100,000,000
29 апреля 2009 г.Дайсуке Такахаши и другие.Открытый суперкомпьютер T2K (640 узлов), скорость одного узла 147,2 гигафлопс, память компьютера 13,5 терабайты, Алгоритм Гаусса – Лежандра, Центр вычислительных наук Университет Цукуба в Цукуба, Япония[33]29.09 часов2,576,980,377,524
ДатаКтоРеализацияВремяДесятичные разряды
(мировые рекорды в смелый)
Все записи, начиная с декабря 2009 г., рассчитываются и проверяются на серверах и / или домашних компьютерах с имеющимися в продаже частями..
31 декабря 2009 г.Фабрис Беллар
  • Процессор Core i7 с тактовой частотой 2,93 ГГц
  • 6 ГиБ (1) ОЗУ
  • 7,5 ТБ дискового хранилища с использованием пяти жестких дисков 1,5 ТБ (модель Seagate Barracuda 7200.11)
  • 64-битный дистрибутив Red Hat Fedora 10
  • Вычисление двоичных цифр: 103 дня
  • Проверка двоичных цифр: 13 дней
  • Преобразование в базу 10: 12 дней
  • Проверка конвертации: 3 дня
  • Проверка двоичных цифр в сети из 9 настольных ПК в течение 34 часов, Алгоритм Чудновского, увидеть [34] для домашней страницы Белларда.[35]
131 день2,699,999,990,000
2 августа 2010 г.Сигеру Кондо[36]
  • используя y-cruncher[37] Александр Йи
  • то Алгоритм Чудновского использовался для основных вычислений
  • при проверке использовались формулы Белларда и Плуффа на разных компьютерах, оба вычисляли 32 шестнадцатеричные цифры, оканчивающиеся на 4,152,410,118,610-ю.
  • с 2 × Intel Xeon X5680 @ 3,33 ГГц - (12 физических ядер, 24 гиперпотоковых)
  • 96 ГиБ DDR3 @ 1066 МГц - (12 × 8 ГиБ - 6 каналов) - Samsung (M393B1K70BH1)
  • 1 ТБ SATA II (загрузочный диск) - Hitachi (HDS721010CLA332), 3 × 2 ТБ SATA II (выход Store Pi) - Seagate (ST32000542AS) 16 × 2 ТБ SATA II (вычисления) - Seagate (ST32000641AS)
  • Windows Server 2008 R2 Enterprise x64
  • Вычисление двоичных цифр: 80 дней
  • Преобразование в базу 10: 8,2 дня
  • Проверка конвертации: 45,6 часа
  • Проверка двоичных цифр: 64 часа (первичная), 66 часов (вторичная)
  • Проверка двоичных цифр производилась одновременно на двух разных компьютерах во время основных вычислений.[38]
90 дней5,000,000,000,000
17 октября 2011 г.Сигеру Кондо[39]
  • используя y-cruncher от Александра Йи
  • Проверка: 1,86 дня и 4,94 дня
371 день10,000,000,000,050
28 декабря 2013 г.Сигеру Кондо[40]
  • используя y-cruncher от Александра Йи
  • с 2 × Intel Xeon E5-2690 @ 2,9 ГГц - (16 физических ядер, 32 гиперпотоковых)
  • 128 ГиБ DDR3 @ 1600 МГц - 8 × 16 ГиБ - 8 каналов
  • Windows Server 2012 x64
  • Проверка: 46 часов
94 дня12,100,000,000,050
8 октября 2014 г.Сандон Нэш Ван Несс "houkouonchi"[41]
  • используя y-cruncher от Александра Йи
  • с 2 × Xeon E5-4650L @ 2,6 ГГц
  • 192 ГиБ DDR3 @ 1333 МГц
  • 24 × 4 ТБ + 30 × 3 ТБ
  • Проверка: 182 часа
208 дней13,300,000,000,000
11 ноября 2016 г.Питер Труб[42][43]
  • используя y-cruncher от Александра Йи
  • с 4 × Xeon E7-8890 v3 @ 2,50 ГГц (72 ядра, 144 потока)
  • 1,25 ТиБ DDR4
  • 20 × 6 ТБ
  • Проверка: 28 часов[44]
105 дней22,459,157,718,361
= ⌊πе × 1012⌋
14 марта 2019 г.Эмма Харука Ивао[45]
  • с помощью y-cruncher v0.7.6
  • Вычисление: 1 × n1-megamem-96 (96 виртуальных ЦП, 1,4 ТБ) с 30 ТБ SSD
  • Хранилище: 24 × n1-standard-16 (16 виртуальных ЦП, 60 ГБ) с 10 ТБ SSD
  • Проверка: 1) 20 часов с использованием 7-членного определения Белларда. Формула BBP 2) 28 часов с использованием 4-членной формулы BBP Плуффа
121 день31,415,926,535,897
= ⌊π × 1013⌋
29 января 2020 г.Тимоти Мулликан[46][47]
  • с помощью y-cruncher v0.7.7
  • Вычисление: 4x Intel Xeon CPU E7-4880 v2 @ 2,50 ГГц
  • ОЗУ 320 ГБ DDR3 PC3-8500R ECC
  • 48 жестких дисков по 6 ТБ (вычисления) + 47 лент LTO Ultrium 5 1,5 ТБ (резервные копии контрольных точек) + 12 жестких дисков по 4 ТБ (хранение цифр)
  • Проверка: 1) 17 часов с использованием семидесятилетия Белларда. Формула BBP 2) 24 часа с использованием 4-членной формулы BBP Плуффа
303 дня50,000,000,000,000

Последние 100 десятичных цифр последнего вычисления мирового рекорда:[48]

1151172718 2444229740 0412605840 3026105553 7774728936  :  49,999,999,999,9508888086663 6658909667 9659924528 1042319124 0640849268  :  50,000,000,000,000

Смотрите также

Часть серия статей на
математическая константа π
3.1415926535897932384626433...
Использует
Свойства
Ценность
люди
История
В культуре
похожие темы

использованная литература

  1. ^ а б c d е ж г час я j k л м п о п q р s т ты v ш Икс y Дэвид Х. Бейли, Джонатан М. Борвейн, Питер Б. Борвейн и Саймон Плафф (1997). «В поисках пи» (PDF). Математический интеллигент. 19 (1): 50–57. Дои:10.1007 / BF03024340. S2CID  14318695.CS1 maint: использует параметр авторов (ссылка на сайт)
  2. ^ Эггелинг, Юлий (1882–1900). Шатапатха-брахман, согласно тексту школы Мадхьяндины. Библиотека Принстонской духовной семинарии. Оксфорд, Кларендон Пресс. С. 302–303.CS1 maint: дата и год (ссылка на сайт)
  3. ^ Священные книги Востока: Сатапатха-Брахмана, pt. 3. Кларендон Пресс. 1894. с. 303. Эта статья включает текст из этого источника, который находится в всеобщее достояние.
  4. ^ «4 II. Сульба сутры». www-history.mcs.st-and.ac.uk.
  5. ^ а б c d е ж Рави П. Агарвал, Ханс Агарвал и Шьямал К. Сен (2013). «Рождение, рост и вычисление числа Пи до десяти триллионов цифр». Успехи в разностных уравнениях. 2013: 100. Дои:10.1186/1687-1847-2013-100.CS1 maint: использует параметр авторов (ссылка на сайт)
  6. ^ Плофкер, Ким (2009). Математика в Индии. Издательство Принстонского университета. ISBN  978-0691120676 - через Google Книги.
  7. ^ https://www.math.rutgers.edu/~cherlin/History/Papers2000/wilson.html
  8. ^ 趙良 五 (1991). 中西 數學 史 的 比較.臺灣 的務印書館. ISBN  978-9570502688 - через Google Книги.
  9. ^ Нидхэм, Джозеф (1986). Наука и цивилизация в Китае: Том 3, Математика и науки о небесах и Земле. Тайбэй: Caves Books, Ltd. Том 3, 100.
  10. ^ а б c Округлено до ближайшего десятичного знака.
  11. ^ Сумка, А. К. (1980). «Индийская литература по математике 1400–1800 гг. Н.э.» (PDF). Индийский журнал истории науки. 15 (1): 86. π ≈ 2,827,433,388,233/9×10−11 = 3,14159 26535 92222…, хорошо до 10 знаков после запятой.
  12. ^ округлено от 2π до 9 шестидесятеричных цифр. Аль-Каши, автор: Адольф Петрович Ющкевич, главный редактор: Борис Александрович Розенфельд, с. 256 О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., "Гияс ад-Дин Джамшид Масуд аль-Каши", Архив истории математики MacTutor, Сент-Эндрюсский университет.. Азарян, Мохаммад К. (2010), «Аль-Рисала аль-Мухитийя: Резюме», Миссурийский журнал математических наук 22 (2): 64–85.
  13. ^ Вьет, Франсуа (1579). Canon mathematicus seu ad triangula: cum adpendicibus (на латыни).
  14. ^ Романус, Адриан (1593). Ideae mathematicae pars prima, sive methodus polygonorum (на латыни). HDL:2027 / мкм. 5320258006.
  15. ^ Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (на латыни). Архивировано из оригинал (PDF) на 2014-02-01.
  16. ^ Хобсон, Эрнест Уильям (1913). «Квадрат круга»: история проблемы (PDF). п. 27.
  17. ^ Ёсио, Миками; Юджин Смит, Дэвид (2004) [1914]. История японской математики (под ред. в мягкой обложке). Dover Publications. ISBN  0-486-43482-6.
  18. ^ Лопес-Ортис, Алекс (20 февраля 1998 г.). «Индиана Билл устанавливает значение Пи равным 3». WWW архив news.answers. Департамент информационных и вычислительных наук Утрехтского университета. Получено 2009-02-01.
  19. ^ Рейтвизнер, Г. (1950). "ENIAC определение π и е до более чем 2000 знаков после запятой ". MTAC. 4: 11–15. Дои:10.1090 / S0025-5718-1950-0037597-6.
  20. ^ Nicholson, S.C .; Джинел, Дж. (1955). "Некоторые комментарии к вычислению NORC π". MTAC. 9: 162–164. Дои:10.1090 / S0025-5718-1955-0075672-5.
  21. ^ Дж. Э. Фелтон, «Электронные компьютеры и математики», Сокращенные материалы Оксфордской математической конференции для школьных учителей и промышленников в Тринити-колледже, Оксфорд, 8–18 апреля 1957 г., стр. 12–17, сноска, стр. 12–53. Этот опубликованный результат верен только для 7480D, как было установлено Фелтоном во время второго расчета с использованием формулы (5), завершенного в 1958 году, но, по-видимому, неопубликованного. Для подробного учета расчетов π увидеть Гаечный ключ, Дж. У. мл. (1960). "Развитие расширенных десятичных приближений к π". Учитель математики. 53: 644–650. Дои:10.5951 / MT.53.8.0644. JSTOR  27956272.
  22. ^ Генуйс, Ф. (1958). "Dix milles decimales de π". Шифр. 1: 17–22.
  23. ^ Это неопубликованное значение Икс до 16167D был рассчитан на системе IBM 704 в Французская комиссия по альтернативным источникам энергии и атомной энергии в Париже с помощью программы Genuys
  24. ^ Шанкс, Дэниел; Гаечный ключ, Джон У. Дж. (1962). "Расчет π до 100 000 знаков после запятой ". Математика вычислений. 16 (77): 76–99. Дои:10.1090 / S0025-5718-1962-0136051-9.
  25. ^ Большие кусочки числа Пи (числовое значение числа Пи достигает 2,16 миллиарда десятичных знаков) Science News 24 августа 1991 г. http://www.encyclopedia.com/doc/1G1-11235156.html
  26. ^ ftp://pi.super-computing.org/README.our_last_record_3b
  27. ^ ftp://pi.super-computing.org/README.our_last_record_4b
  28. ^ ftp://pi.super-computing.org/README.our_last_record_6b
  29. ^ ftp://pi.super-computing.org/README.our_last_record_51b
  30. ^ ftp://pi.super-computing.org/README.our_last_record_68b
  31. ^ ftp://pi.super-computing.org/README.our_latest_record_206b
  32. ^ «Архивная копия». Архивировано из оригинал на 2011-03-12. Получено 2010-07-08.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
  33. ^ «Архивная копия». Архивировано из оригинал на 2009-08-23. Получено 2009-08-18.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
  34. ^ "Домашняя страница Фабриса Беллара". bellard.org. Получено 28 августа 2015.
  35. ^ http://bellard.org/pi/pi2700e9/pipcrecord.pdf
  36. ^ "Пи-мир". calico.jp. Архивировано из оригинал 31 августа 2015 г.. Получено 28 августа 2015.
  37. ^ "y-cruncher - многопоточная программа Pi". numberworld.org. Получено 28 августа 2015.
  38. ^ «Пи - 5 триллионов цифр». numberworld.org. Получено 28 августа 2015.
  39. ^ «Пи - 10 триллионов цифр». numberworld.org. Получено 28 августа 2015.
  40. ^ «Пи - 12,1 триллиона цифр». numberworld.org. Получено 28 августа 2015.
  41. ^ "y-cruncher - многопоточная программа Pi". numberworld.org. Получено 14 марта 2018.
  42. ^ "pi2e". pi2e.ch. Получено 15 ноября 2016.
  43. ^ Александр Дж. Йи. "y-cruncher - многопоточная программа Pi". numberworld.org. Получено 15 ноября 2016.
  44. ^ «Шестнадцатеричные цифры верны! - pi2e триллион цифр числа пи». pi2e.ch. Получено 15 ноября 2016.
  45. ^ "Google Cloud опровергает рекорд Пи". Получено 14 марта 2019.
  46. ^ «Запись Pi возвращается на персональный компьютер». Получено 30 января 2020.
  47. ^ «Расчет числа Пи: моя попытка побить мировой рекорд числа Пи». Получено 30 января 2020.
  48. ^ "Файл проверки". Numberworld. 7 марта 2020.

внешние ссылки