Гиперконъюгация - Hyperconjugation

В органическая химия, сверхсопряжение (или σ-сопряжение) относится к делокализации электронов с участием связей преимущественно σ-характера. Обычно гиперконъюгация включает взаимодействие электроны в сигма (σ) орбитальная (например, C – H или C – C) с соседней незаселенной несвязанной p или разрушение σ * или π * орбитали дать пару расширенных молекулярные орбитали. Однако иногда низколежащие разрыхляющие σ * -орбитали могут также взаимодействовать с заполненными орбиталями неподеленного парного характера (n) в так называемом «отрицательном сверхсопряжении».[1] Повышенная делокализация электронов, связанная с гиперконъюгацией, увеличивает стабильность системы.[2][3] В частности, новая орбиталь со связующим характером стабилизируется, что приводит к общей стабилизации молекулы.[4] Только электроны в связях, которые находятся в положение β может иметь такой вид прямого стабилизирующего эффекта - отдавать сигма-связь атома орбитали в другом атоме, непосредственно присоединенном к нему. Однако расширенные версии гиперконъюгации (такие как двойное гиперспряжение[5]) тоже может быть важным. В Эффект Бейкера – Натана, иногда используется как синоним гиперконъюгации,[6] это конкретное приложение его к определенным химическим реакциям или типам структур.[7]

Гиперконъюгация: перекрытие орбиталей σ-орбитали и π * -орбитали стабилизирует алкилзамещенные алкены. Орбиталь σ (сплошной цвет) закрашена, а орбиталь π * (выделена серым цветом) - это незаселенная разрыхляющая орбиталь. Ref. Клейден, Гривс, Уоррен

Приложения

Гиперконъюгацию можно использовать для объяснения множества химических явлений, включая аномерный эффект, то безвкусный эффект, то вращающийся барьер из этан, то бета-кремний эффект, то частота колебаний из экзоциклический карбонил групп, и относительная стабильность замещенных карбокатионы и замещенный углерод с центром радикалы, а термодинамический Правление Зайцева для устойчивости к алкенам. Более спорно, сверхсопряжения предложен квантово-механического моделирования, чтобы быть лучшим объяснением для предпочтения шахматное строение а не старое хрестоматийное понятие стерическое препятствие.[8][9]

Влияние на химические свойства

Гиперконъюгация влияет на несколько свойств.[6][10]

  1. Длина скрепления: Гиперконъюгация считается ключевым фактором в сокращении сигма-облигации (σ-связи). Например, одинарные связи C – C в 1,3-бутадиен и Пропин имеют длину примерно 1,46 ангстрем, что намного меньше, чем значение около 1,54 Å, найденное в насыщенных углеводороды. Для бутадиена это можно объяснить нормальным сопряжением двух алкенильных частей. Но для пропина - сверхсопряжение между алкильной и алкинильной частями.
  2. Дипольные моменты: Большое увеличение дипольного момента 1,1,1-трихлорэтан по сравнению с хлороформ можно отнести к гиперконъюгированным структурам.
  3. В теплота образования молекул с гиперсопряжением больше, чем сумма их энергий связи, а теплота гидрирования на двойную связь меньше, чем теплота гидрирования этилен.
  4. Стабильность карбокатионы:
    (CH3)3C+ > (CH3)2CH+ > (CH3) CH2+ > CH3+
    Три C – H σ-связи метильной группы (ей), присоединенной к карбокатиону, могут претерпевать стабилизационное взаимодействие, но только одна из них может быть идеально выровнена с пустой p-орбиталью, в зависимости от конформации углерод-углеродной связи. Пожертвование от двух смещенных связей C – H слабее.[11] Чем больше имеется соседних метильных групп, тем выше стабилизация гиперконъюгации из-за увеличения числа соседних связей C – H.

Гиперконъюгация в непредельных соединениях

Гиперконъюгация была предложена как причина повышенной стабильности углерод-углеродных двойных связей по мере увеличения степени замещения. Ранние исследования гиперконъюгации были выполнены в исследовательской группе Георгий Кистяковский. Их работа, впервые опубликованная в 1937 году, была задумана как предварительный отчет о ходе термохимических исследований изменений энергии во время реакции присоединения различных ненасыщенный и циклические соединения. Важность гиперсопряжения для объяснения этого эффекта получила подтверждение в квантово-химических расчетах.[12] Ключевым взаимодействием считается передача электронной плотности от соседней связи C – H σ на π * разрыхляющую орбиталь алкена (σC – H→ π *). Эффект почти на порядок слабее, чем в случае алкильного замещения на карбокатионы (σC – H→ пC), поскольку незаполненная p-орбиталь имеет меньшую энергию и, следовательно, лучше энергетически согласована с σ-связью. Когда этот эффект проявляется в образовании более замещенного продукта в термодинамически контролируемых реакциях E1, он известен как Правление Зайцева, хотя во многих случаях кинетический продукт также следует этому правилу. (Увидеть Правило Гофмана для случаев, когда кинетический продукт является менее замещенным.)

Одна серия экспериментов Кистяковского включала собранные плавки гидрирование данные во время газофазных реакций ряда соединений, содержащих один алкен Блок. При сравнении диапазона моноалкил -замещенные алкены, они обнаружили, что любая алкильная группа заметно увеличивает стабильность, но выбор различных конкретных алкильных групп практически не влияет.[13]

Часть работы Кистяковского включала сравнение других непредельных соединений в форме CH2= CH (CH2) n-CH = CH2 (п = 0,1,2). Эти эксперименты показали важный результат; когда n = 0, возникает эффект сопряжения с молекулой, при котором значение ΔH уменьшается на 3,5 ккал. Это можно сравнить с присоединением двух алкильных групп к этилену. Кистяковский также исследовал системы с открытой цепью, в которых наибольшее количество выделяемого тепла было обнаружено при присоединении к молекуле в 1,4-положении. Циклические молекулы оказались наиболее проблематичными, поскольку было обнаружено, что напряжение молекулы следует учитывать. Напряжение пятичленных колец возрастает с уменьшением степени ненасыщенности. Это был неожиданный результат, который впоследствии был исследован в работе с циклическими ангидриды кислот и лактоны. Циклические молекулы типа бензол и его производные также были изучены, поскольку их поведение отличалось от поведения других ненасыщенных соединений.[13]

Несмотря на тщательность работы Кистяковского, она не была полной и требовала дополнительных доказательств, подтверждающих его выводы. Его работа стала важным первым шагом к зарождению идей гиперконъюгации и эффектов конъюгации.

Стабилизация 1,3-бутадиена и 1,3-бутадиена

В спряжение из 1,3-бутадиен был впервые оценен Кистяковским, конъюгативный вклад 3,5 ккал / моль был обнаружен на основе энергетического сравнения гидрирование между конъюгированными видами и неконъюгированными аналогами.[13] Роджерс, который использовал метод, впервые примененный Кистяковским, сообщил, что стабилизация конъюгации 1,3-бутадиин равнялась нулю, так как разность ΔгидН между первым и вторым гидрированием был равен нулю. Теплоты гидрирования (ΔгидH) были получены методом вычислительной квантовой химии G3 (MP2).[14]

Стабилизация нулевого сопряжения Роджерса 1,3-butadiyne.png

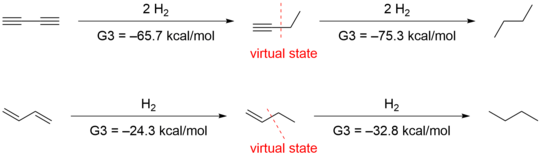
Другая группа во главе с Хоуком[15] предположил, что методы, использованные Роджерсом и Кистяковски, неуместны, потому что сравнение теплоты гидрирования оценивает не только эффекты конъюгации, но и другие структурные и электронные различия. Они получили -70,6 ккал / моль и -70,4 ккал / моль для первого и второго гидрирования соответственно путем ab initio расчет, который подтвердил данные Роджерса. Однако они интерпретировали данные по-разному, учитывая стабилизацию гиперконъюгации. Для количественной оценки эффекта гиперконъюгации они разработали следующие изодесмические реакции в 1-бутин и 1-бутен.

Самодельная сопряженная стабилизация Хука и Шлейера.png

Удаление гиперконъюгативных взаимодействий дает виртуальные состояния с энергиями на 4,9 и 2,4 ккал / моль выше, чем у 1-бутин и 1-бутен соответственно. Использование этих виртуальных состояний приводит к конъюгированной стабилизации 9,6 ккал / моль для 1,3-бутадиена и 8,5 ккал / моль для 1,3-бутадиена.

Виртуальные состояния в дииновой сопряженной стабилизации Хука и Шлейера.png

Тенденции гиперконъюгации

Относительно недавняя работа (2006) Фернандеса и Френкинга (2006) суммировала тенденции гиперконъюгации среди различных групп ациклических молекул, используя анализ энергетического разложения или EDA. Фернандес и Френкинг определяют этот тип анализа как «... метод, который использует только пи-орбитали взаимодействующих фрагментов в геометрии молекулы для оценки пи-взаимодействий.[16]«Для этого типа анализа образование связей между различными молекулярными фрагментами представляет собой комбинацию трех составляющих. ΔEЭльстат представляет собой то, что Фернандес и Френкинг называют «квазиклассическим электростатическим притяжением молекулы».[16]”Второй член ΔEПаули, представляет собой отталкивание Паули молекулы. ΔEсфера, третий член представляет собой стабилизирующие взаимодействия между орбиталями и определяется как сумма ΔEПи и ΔEсигма. Полная энергия взаимодействия ΔEint, является результатом суммы трех членов.[16]

Группа, у которой ΔEПи ценности были очень тщательно проанализированы группой Enones которые различались заместителем.

Enone.jpg

Фернандес и Френкинг сообщили, что метил, гидроксил, и амино- заместители приводили к уменьшению ΔEПи от родителя 2-пропенал. Наоборот, галогенид заместители с возрастающей атомной массой приводили к увеличению ΔEПи. Потому что и enone study, и Hammett анализ изучают эффекты заместителей (хотя и у разных видов), Фернандес и Френкинг считают, что сравнение этих двух для исследования возможных тенденций может дать существенное понимание их собственных результатов. Они наблюдали линейную зависимость между ΔEПи значения для замещенных енонов и соответствующие константы Гаммета. Наклон графика составил -51,67 с коэффициентом корреляции -0,97 и стандартным отклонением 0,54.[16] Фернандес и Френкинг заключают из этих данных, что ... «электронные эффекты заместителей R на конъюгацию pi в гомо- и гетероконъюгированных системах подобны и, таким образом, кажутся довольно независимыми от природы конъюгированной системы».[16][17]

Вращательный барьер из этана

Примером, когда гиперконъюгация может не рассматриваться как возможное химическое объяснение, является рационализация вращательный барьер этана (C2H6). Еще в 1930-е годы считалось, что шахматные конформации этана были более стабильными, чем затмение. Уилсон доказал, что энергетический барьер между любой парой затменных и шахматных конформаций составляет приблизительно 3 ккал / моль, и общепринятым обоснованием этого было неблагоприятное стерические взаимодействия между атомами водорода.

Проекции Ньюмана: в шахматном порядке (слева) и затмевающемся (справа)

Однако в своей статье 2001 года Пофристик и Гудман[8] выяснилось, что это объяснение может быть слишком упрощенным.[18] Гудман сосредоточился на трех основных физических факторах: сверхсопряженных взаимодействиях, обменном отталкивании, определяемом Принцип исключения Паули, и электростатические взаимодействия (Кулоновские взаимодействия ). Путем сравнения традиционной молекулы этана и гипотетической молекулы этана с удаленными всеми обменными отталкиваниями, потенциальные кривые были построены путем построения графика крутильный угол в зависимости от энергии для каждой молекулы. Анализ кривых показал, что ступенчатая конформация не имеет связи с величиной электростатического отталкивания внутри молекулы. Эти результаты демонстрируют, что кулоновские силы не объясняют предпочтительные шахматные конформации, несмотря на тот факт, что растяжение центральной связи снижает электростатические взаимодействия.[8]

Гудман также провел исследования, чтобы определить вклад вицинальный (между двумя метильными группами) против геминальных (между атомами в одной метильной группе) взаимодействия с гиперконъюгацией. В отдельных экспериментах геминальное и вицинальное взаимодействия были удалены, и был выведен наиболее стабильный конформер для каждого взаимодействия.[8]

Расчетный угол скручивания этана с удаленными гиперконъюгативными эффектами
Удаленное взаимодействиеКрутильный уголСоответствующий конформер
Никто60°В шахматном порядке
Все гиперконъюгации0°Затмили
Вицинальное гиперконъюгация0°Затмили
Близнецы гиперконъюгации60°В шахматном порядке

Из этих экспериментов можно сделать вывод, что сверхсопряженные эффекты делокализуют заряд и стабилизируют молекулу. Кроме того, именно вицинальные гиперконъюгативные эффекты удерживают молекулу в шахматной конформации.[8] Благодаря этой работе в настоящее время более принята следующая модель стабилизации ступенчатой ​​конформации этана:

На основе рисунка из Schreiner (2002)

Гиперсопряжение может также объяснить несколько других явлений, объяснения которых также могут быть не такими интуитивными, как объяснение вращательного барьера этана.[18]

Вопрос о вращательном барьере этана не решен в научном сообществе. Анализ в рамках количественного теория молекулярных орбиталей показывает, что 2-орбитально-4-электронное (стерическое) отталкивание преобладает над гиперконъюгацией.[19] А теория валентной связи исследование также подчеркивает важность стерических эффектов.[20]

Смотрите также

использованная литература

  1. ^ ИЮПАК, Сборник химической терминологии 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) "сверхсопряжение ". Дои:10.1351 / goldbook.H02924
  2. ^ Джон Макмерри. Органическая химия, 2-е изд. ISBN  0-534-07968-7
  3. ^ Алабугин, И.В .; Gilmore, K .; Петерсон, П. (2011). «Гиперсопряжение». ПРОВОДА Comput Mol Sci. 1: 109–141. Дои:10.1002 / wcms.6.
  4. ^ Смешанная орбиталь антисвязывающего характера фактически имеет повышенную энергию по сравнению с исходной антисвязывающей орбиталью. Однако, поскольку разрыхляющая орбиталь в большинстве случаев остается незаселенной, это обычно не влияет на энергию системы.
  5. ^ Алабугин, И. В. (2016) Дистанционные стереоэлектронные эффекты, в Стереоэлектронные эффекты: мост между структурой и реакционной способностью, John Wiley & Sons, Ltd, Чичестер, Великобритания. Дои:10.1002 / 9781118906378.ch8
  6. ^ а б Дизи, К. (1945). «Гиперсопряжение». Chem. Ред. 36 (2): 145–155. Дои:10.1021 / cr60114a001.
  7. ^ Мадан, Р.Л. (2013). «4.14: гиперспряжение или резонанс без связи». Органическая химия. Тата МакГроу – Хилл. ISBN  9789332901070.
  8. ^ а б c d е Pophristic, V .; Гудман, Л. (2001). «Гиперконъюгация нестерического отталкивания приводит к шахматной структуре этана». Природа. 411 (6837): 565–8. Дои:10.1038/35079036. PMID  11385566.
  9. ^ Фрэнк Вайнхольд (2001). «Химия. Новый поворот в молекулярной форме». Природа. 411 (6837): 539–41. Дои:10.1038/35079225. PMID  11385553.
  10. ^ Schmeising, H.N .; и другие. (1959). «Повторная оценка конъюгации и гиперконъюгации: влияние изменений гибридизации на углеродные связи». Тетраэдр. 5 (2–3): 166–178. Дои:10.1016/0040-4020(59)80102-2.
  11. ^ Алабугин, Игорь В .; Бреш, Стефан; душ Пассос Гомеш, Габриэль (2014). «Орбитальная гибридизация: ключевой электронный фактор в управлении структурой и реактивностью». Журнал физической органической химии. 28: 147–162. Дои:10.1002 / poc.3382.
  12. ^ Брейда, Бенуа; Прана, Винча; Гиберти, Филипп С. (2009). «Физическое происхождение правила Сайцева». Angewandte Chemie International Edition. 48 (31): 5724–5728. Дои:10.1002 / anie.200901923. ISSN  1521-3773. PMID  19562814.
  13. ^ а б c Кистяковский, Г. Б .; и другие. (1937). «Энергетические изменения, связанные с реакциями присоединения ненасыщенных углеводородов». Chem. Ред. 20 (2): 181–194. Дои:10.1021 / cr60066a002.
  14. ^ Роджерс, Д. W .; и другие. (2003). «Стабилизация конъюгации 1,3-бутадиина равна нулю». Орг. Lett. 5 (14): 2373–5. Дои:10.1021 / ol030019h. PMID  12841733.
  15. ^ Houk, K.N .; и другие. (2004). «Насколько велика сопряженная стабилизация Diynes?». Варенье. Chem. Soc. 126 (46): 15036–7. Дои:10.1021 / ja046432h. PMID  15547994.
  16. ^ а б c d е Фернандес, И., Френкинг, Г. (2006). "Прямая оценка силы сопряжения и гиперконъюгации методом анализа разложения энергии". Chem. Евро. Дж. 12 (13): 3617–29. Дои:10.1002 / chem.200501405. PMID  16502455.CS1 maint: несколько имен: список авторов (ссылка на сайт)
  17. ^ См. Ссылку 12 для получения графика и его полного анализа.
  18. ^ а б Шрейнер, П. (2002). «Обучение правильным причинам: уроки ошибочного происхождения вращательного барьера в этане». Энгью. Chem. Int. Эд. 41 (19): 3579–81, 3513. Дои:10.1002 / 1521-3773 (20021004) 41:19 <3579 :: AID-ANIE3579> 3.0.CO; 2-S. PMID  12370897.
  19. ^ Bickelhaupt, F.M .; Баэрэндс (2003). «Случай стерического отталкивания, вызывающего ступенчатую конформацию этана». Энгью. Chem. Int. Эд. 42 (35): 4183–4188. Дои:10.1002 / anie.200350947. PMID  14502731.
  20. ^ Mo, Y.R .; и другие. (2004). «Величина гиперконъюгации в этане: перспектива с ab initio теории валентной связи». Энгью. Chem. Int. Эд. 43 (15): 1986–1990. Дои:10.1002 / anie.200352931. PMID  15065281.

внешние ссылки