Многомерная выборка - Multidimensional sampling

В цифровая обработка сигналов, многомерная выборка это процесс преобразования функции многомерная переменная в дискретный набор значений функции, измеренных на дискретном множестве точек. В этой статье представлен основной результат Петерсена и Миддлтона.^[1] на условиях безупречной реконструкции волновое число -ограниченная функция по измерениям на дискретной решетка очков. Этот результат, также известный как Теорема Петерсена – Миддлтона, является обобщением Теорема выборки Найквиста – Шеннона для выборки одномерного ограниченный диапазон функции в многомерные Евклидовы пространства.

По сути, теорема Петерсена – Миддлтона показывает, что функция с ограниченным волновым числом может быть полностью восстановлена ​​по ее значениям на бесконечной решетке точек при условии, что решетка достаточно тонкая. Теорема дает условия на решетку, при которых возможно точное восстановление.

Как и теорема выборки Найквиста – Шеннона, эта теорема также предполагает идеализацию любой реальной ситуации, поскольку она применима только к функциям, выборка которых производится по бесконечному количеству точек. Идеальная реконструкция математически возможна для идеализированной модели, но только приближение для реальных функций и методов выборки, хотя на практике часто очень хорошее.

Предварительные мероприятия

Этот раздел включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. Пожалуйста, помогите улучшать этот раздел введение более точные цитаты. (Октябрь 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Рис.1: Гексагональная решетка для отбора проб ${ displaystyle Lambda}$ и его базисные векторы v₁ и v₂

Рис.2: Обратная решетка ${ displaystyle Gamma}$ соответствующей решетке ${ displaystyle Lambda}$ рис.1 и его базисные векторы ты₁ и ты₂ (рисунок не в масштабе).

Концепция ограниченный диапазон Функция в одном измерении может быть обобщена до понятия функции с ограниченным волновым числом в более высоких измерениях. Напомним, что преобразование Фурье интегрируемой функции ${ Displaystyle е ( cdot)}$ на п-мерное евклидово пространство определяется как:

${ Displaystyle { шляпа {f}} ( xi) = { mathcal {F}} (f) ( xi) = int _ { Re ^ {n}} f (x) e ^ {- 2 pi i langle x, xi rangle} , dx}$

куда Икс и ξ находятся п-размерный векторов, и ${ Displaystyle langle х, xi rangle}$ это внутренний продукт векторов. Функция ${ Displaystyle е ( cdot)}$ считается, что волновое число ограничено набором ${ displaystyle Omega}$ если преобразование Фурье удовлетворяет ${ Displaystyle { шляпа {f}} ( xi) = 0}$ за ${ displaystyle xi notin Omega}$.

Точно так же конфигурацию равномерно расположенных точек выборки в одномерном пространстве можно обобщить на решетка в высших измерениях. Решетка - это набор точек ${ Displaystyle Lambda subset Re ^ {n}}$ формы ${ displaystyle Lambda = left { sum _ {i = 1} ^ {n} a_ {i} v_ {i} ; | ; a_ {i} in mathbb {Z} right } }$куда {v₁, ..., v_п} это основа за ${ Displaystyle Re ^ {п}}$. В обратная решетка ${ displaystyle Gamma}$ соответствующий ${ displaystyle Lambda}$ определяется

${ Displaystyle Gamma = left { sum _ {i = 1} ^ {n} a_ {i} u_ {i} ; | ; a_ {i} in mathbb {Z} right } }$

где векторы ${ displaystyle u_ {i}}$ выбраны для удовлетворения ${ displaystyle langle u_ {i}, v_ {j} rangle = delta _ {ij}}$. То есть, если векторы ${ displaystyle u_ {i}}$ формировать столбцы матрицы ${ displaystyle A}$ и ${ displaystyle v_ {i}}$ столбцы матрицы ${ displaystyle B}$, тогда ${ displaystyle A = B ^ {- T}}$. Примером выборочной решетки в двумерном пространстве является шестиугольная решетка изображена на рисунке 1. Соответствующая обратная решетка показана на рисунке 2. Обратная решетка квадратная решетка в двух измерениях - это еще одна квадратная решетка. В трехмерном пространстве обратная решетка гранецентрированная кубическая (ГЦК) решетка является объемноцентрированной кубической (ОЦК) решеткой.

Теорема

Позволять ${ displaystyle Lambda}$ обозначим решетку в ${ Displaystyle Re ^ {п}}$ и ${ displaystyle Gamma}$ соответствующая обратная решетка. Теорема Петерсена и Миддлтона^[1] утверждает, что функция ${ Displaystyle е ( cdot)}$ это ограниченное волновым числом набор ${ displaystyle Omega subset Re ^ {n}}$ можно точно восстановить по его измерениям на ${ displaystyle Lambda}$ при условии, что набор ${ displaystyle Omega}$ не пересекается ни с одной из его сдвинутых версий ${ displaystyle Omega + x}$ где сдвиг Икс - любой ненулевой элемент обратной решетки ${ displaystyle Gamma}$. Другими словами, ${ Displaystyle е ( cdot)}$ можно точно восстановить по его измерениям на ${ displaystyle Lambda}$ при условии, что ${ Displaystyle Omega cap {x + y: y in Omega } = phi}$ для всех ${ Displaystyle х ин гамма setminus {0 }}$.

Реконструкция

Рис. 3: Поддержка дискретизированного спектра ${ displaystyle { hat {f}} _ {s} ( cdot)}$ полученный гексагональной выборкой двумерной функции, ограниченной волновым числом круглого диска. Синий круг представляет опору ${ displaystyle Omega}$ исходного поля, ограниченного волновым числом, а зеленые кружки представляют повторения. В этом примере спектральные повторения не перекрываются и, следовательно, нет наложения спектров. Исходный спектр можно точно восстановить из отобранного спектра.

Обобщение Формула суммирования Пуассона в более высокие измерения ^[2] может использоваться, чтобы показать, что образцы, ${ Displaystyle {е (х): х в лямбда }}$, функции ${ Displaystyle е ( cdot)}$ на решетке ${ displaystyle Lambda}$ достаточно для создания периодическое суммирование функции ${ Displaystyle { шляпа {f}} ( cdot)}$. Результат:

${ displaystyle { hat {f}} _ {s} ( xi) { stackrel { mathrm {def}} {=}} sum _ {y in Gamma} { hat {f}} left ( xi -y right) = sum _ {x in Lambda} | Lambda | f (x) e ^ {- i2 pi langle x, xi rangle},}$

(Уравнение 1)

куда ${ displaystyle | Lambda |}$ представляет собой объем параллелепипед образованные векторами {v₁, ..., v_п}. Эту периодическую функцию часто называют дискретным спектром, и ее можно интерпретировать как аналог функции преобразование Фурье с дискретным временем (DTFT) в более высоких измерениях. Если исходный спектр, ограниченный волновым числом ${ Displaystyle { шляпа {f}} ( cdot)}$ поддерживается на съемочной площадке ${ displaystyle Omega}$ тогда функция ${ Displaystyle { шляпа {f}} _ {s} ( cdot)}$ поддерживается при периодическом повторении ${ displaystyle Omega}$ сдвинутые точками на обратной решетке ${ displaystyle Gamma}$. Если выполняются условия теоремы Петерсена-Миддлтона, то функция ${ Displaystyle { шляпа {f}} _ {s} ( xi)}$ равно ${ Displaystyle { шляпа {f}} ( xi)}$ для всех ${ displaystyle xi in Omega}$, и, следовательно, исходное поле может быть точно восстановлено по образцам. В этом случае реконструированное поле совпадает с исходным полем и может быть выражено в терминах выборок как

${ displaystyle f (x) = sum _ {y in Lambda} | Lambda | f (y) { check { chi}} _ { Omega} (y-x)}$,

(Уравнение 2)

куда ${ displaystyle { check { chi}} _ { Omega} ( cdot)}$ является обратным преобразованием Фурье характеристическая функция из набора ${ displaystyle Omega}$. Эта интерполяционная формула является многомерным эквивалентом формулы Формула интерполяции Уиттекера – Шеннона.

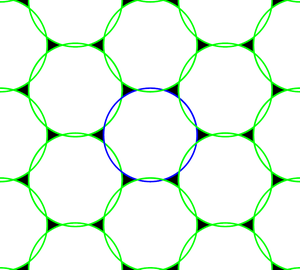
В качестве примера предположим, что ${ displaystyle Omega}$ представляет собой круговой диск. Рисунок 3 иллюстрирует поддержку ${ Displaystyle { шляпа {f}} _ {s} ( cdot)}$ при выполнении условий теоремы Петерсена-Миддлтона. Мы видим, что спектральные повторения не перекрываются и, следовательно, исходный спектр может быть точно восстановлен.

Подразумеваемое

Сглаживание

Рис. 4: Поддержка дискретизированного спектра ${ Displaystyle { шляпа {f}} _ {s} ( cdot)}$ полученный гексагональной выборкой двумерной функции, ограниченной волновым числом круглого диска. В этом примере решетка дискретизации недостаточно тонкая и, следовательно, диски перекрываются в спектре дискретизации. Таким образом, спектр внутри ${ displaystyle Omega}$ представленный синим кружком, не может быть восстановлен точно из-за перекрытия повторений (показано зеленым), что приводит к наложению.

Рис. 5: Пространственное наложение в форме Муаровый узор.

Рис. 6: Изображение кирпичной стены с правильной выборкой.

Теорема дает условия на выборочные решетки для точного восстановления выборки. Если решетки недостаточно тонкие, чтобы удовлетворять условию Петерсена-Миддлтона, то поле не может быть восстановлено точно по образцам в целом. В этом случае мы говорим, что образцы могут быть псевдоним. Снова рассмотрим пример, в котором ${ displaystyle Omega}$ представляет собой круговой диск. Если условия Петерсена-Миддлтона не выполняются, поддержка дискретизированного спектра будет такой, как показано на рисунке 4. В этом случае спектральные повторения перекрываются, что приводит к наложению спектров при реконструкции.

Простую иллюстрацию алиасинга можно получить, изучив изображения с низким разрешением. Полутоновое изображение можно интерпретировать как функцию в двухмерном пространстве. Пример сглаживания показан на изображениях кирпичных узоров на рисунке 5. Изображение показывает эффекты сглаживания, когда условие теоремы выборки не выполняется. Если решетка пикселей недостаточна для сцены, возникает наложение, о чем свидетельствует появление Муаровый узор в полученном изображении. Изображение на рисунке 6 получается, когда сглаженная версия сцены дискретизируется с той же решеткой. В этом случае условия теоремы выполняются и наложения спектров не происходит.

С.П. Ефимов из Московский государственный технический университет им. Н. Э. Баумана в 1978 г. нашел способ облегчить ограничения для области спектра.^[3] Он считал, что N идентичных решеток выборок произвольно сдвинуты друг к другу. Оптимальная выборка действительна для области спектра, в которой смещенные версии плотно упакованы N раз на обратной решетке. Следовательно, кольцо может быть перекрыто набором шестиугольников вместо одного. JWST Матрица телескопов состоит из 18 шестиугольников. Выборка на 18 смещенных решетках возможна для 2-мерного преобразования Фурье сигнала матрицы (то есть для излучаемого сигнала).

Оптимальные решетки для отбора проб

Одной из задач, представляющих интерес при разработке схемы выборки для полей с ограниченным волновым числом, является определение конфигурации точек, которая приводит к минимальной плотности выборки, то есть плотности точек выборки на единицу пространственного объема в ${ Displaystyle Re ^ {п}}$. Обычно стоимость снятия и хранения измерений пропорциональна используемой плотности выборки. Часто на практике естественным подходом к выборке двумерных полей является ее выборка в точках на прямоугольная решетка. Однако это не всегда идеальный выбор с точки зрения плотности выборки. Теорема Петерсена и Миддлтона может быть использована для определения оптимальной решетки для выборочных полей, волновое число которых ограничено заданным набором. ${ Displaystyle Omega subset Re ^ {d}}$. Например, можно показать, что решетка в ${ Displaystyle Re ^ {2}}$ с минимальной пространственной плотностью точек, которая допускает точную реконструкцию полей, ограниченных волновым числом кругового диска в ${ Displaystyle Re ^ {2}}$ - гексагональная решетка.^[4] Как следствие, для отбора проб предпочтительны гексагональные решетки. изотропные поля в ${ Displaystyle Re ^ {2}}$.

Оптимальные решетки выборки были изучены в более высоких измерениях.^[5] Как правило, оптимальный упаковка сфер решетки идеально подходят для выборки гладких случайных процессов, в то время как решетки с оптимальным покрытием сфер^[6] идеально подходят для выборки грубых случайных процессов.

Поскольку оптимальные решетки, вообще говоря, неразделимы, проектируя интерполяция и фильтры реконструкции требует механизмов проектирования фильтров без тензорного произведения (т. е. неразрывных). Коробчатые шлицы обеспечивают гибкую основу для проектирования такой неразрывной реконструкции FIR фильтры, которые можно геометрически подогнать под каждую решетку.^[7][8] Шестигранные шлицы^[9] являются обобщением B-шлицы для двумерных гексагональных решеток. Точно так же в трехмерных и более высоких измерениях шлицы Вороного^[10] дать обобщение B-шлицы которые можно использовать для разработки неразделимых КИХ-фильтров, геометрически адаптированных для любой решетки, включая оптимальные решетки.

Явное построение идеальных фильтров нижних частот (т. Е. грех функции), обобщенные на оптимальные решетки, возможно при изучении геометрических свойств Зоны Бриллюэна (т.е. ${ displaystyle Omega}$ выше) этих решеток (которые зонотопы ).^[11] Этот подход обеспечивает явное представление в закрытой форме ${ displaystyle { check { chi}} _ { Omega} ( cdot)}$ для общих решеток, включая оптимальные выборочные решетки. Эта конструкция дает обобщение Фильтр Ланцоша в 1-D в многомерную постановку для оптимальных решеток.^[11]

Приложения

Теорема Петерсена – Миддлтона полезна при разработке эффективных стратегий размещения датчиков в приложениях, включающих измерение пространственных явлений, таких как сейсмические исследования, мониторинг окружающей среды и измерения пространственного звукового поля.

Рекомендации