Теория массового обслуживания - Queueing theory
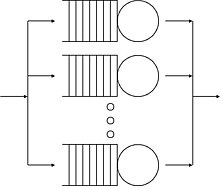
Теория массового обслуживания математическое исследование очередей, или очереди.[1] Модель организации очередей построена таким образом, чтобы можно было предсказать длину очереди и время ожидания.[1] Теория массового обслуживания обычно считается разделом исследование операций потому что результаты часто используются при принятии бизнес-решений о ресурсах, необходимых для предоставления услуги.
Теория массового обслуживания берет свое начало в исследованиях Агнер Краруп Эрланг когда он создавал модели для описания системы компании Copenhagen Telephone Exchange, датской компании.[1] С тех пор эти идеи нашли применение, в том числе телекоммуникации, транспортная инженерия, вычисление[2]и особенно в промышленная инженерия, в проектировании заводов, магазинов, офисов и больниц, а также в управлении проектами.[3][4]
Написание
Написание «в очереди» над «очередью» обычно встречается в области академических исследований. Фактически, один из ведущих профессиональных журналов - это Системы массового обслуживания.
Одиночные узлы очередей
Очередь или узел очередей можно рассматривать как почти черный ящик. Задания или «клиенты» прибывают в очередь, возможно, ждут какое-то время, требуют некоторого времени для обработки и затем удаляются из очереди.
Однако узел организации очереди - это не совсем чистый черный ящик, поскольку необходима некоторая информация о внутренней части узла очереди. Очередь имеет один или несколько «серверов», каждый из которых может быть связан с поступающим заданием до тех пор, пока он не уйдет, после чего этот сервер будет свободен для соединения с другим поступающим заданием.
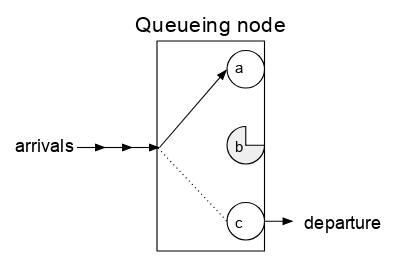
Часто используется аналогия с кассиром в супермаркете. Существуют и другие модели, но эта часто встречается в литературе. Клиенты прибывают, обрабатываются кассиром и уходят. Каждый кассир обрабатывает одного клиента за раз, и, следовательно, это узел очереди только с одним сервером. Настройка, при которой покупатель немедленно уходит, если кассир занят, когда приходит покупатель, называется очередью без буфера (или без «зоны ожидания» или аналогичных терминов). Обстановка с зоной ожидания на срок до п клиентов называется очередью с размером буфера п.
Процесс рождения-смерти
Поведение отдельной очереди (также называемой «узлом очереди») может быть описано с помощью процесс рождения – смерти, который описывает поступления и выбывания из очереди, а также количество заданий (также называемых «клиентами» или «запросами» или любое количество других вещей, в зависимости от поля), находящихся в настоящее время в системе. Прибытие увеличивает количество вакансий на 1, а отъезд (работа, завершающая свою услугу) уменьшается. k Автор: 1.


Уравнения баланса
В устойчивое состояние уравнения для процесса рождения и смерти, известного как уравнения баланса, являются следующими. Здесь обозначает вероятность устойчивого состояния быть в состоянии п.
Первые два уравнения подразумевают
и
По математической индукции
Условие приводит к:
что вместе с уравнением для , полностью описывает требуемые вероятности установившегося состояния.
Обозначения Кендалла
Одиночные узлы очередей обычно описываются с помощью Обозначения Кендалла в виде A / S /c куда А описывает распределение продолжительности между каждым поступлением в очередь, S распределение времени обслуживания для рабочих мест и c количество серверов в узле.[5][6] В качестве примера обозначений M / M / 1 очередь это простая модель, в которой один сервер обслуживает задания, поступающие в соответствии с Пуассоновский процесс (где продолжительность между прибытием экспоненциально распределенный ) и имеют экспоненциально распределенное время обслуживания (M обозначает Марковский процесс ). В Очередь M / G / 1, G означает «общий» и указывает на произвольный распределение вероятностей на время обслуживания.
Пример анализа очереди M / M / 1
Рассмотрим очередь с одним сервером и следующими характеристиками:
- λ: частота прибытия (ожидаемое время между прибытием каждого клиента, например, 30 секунд);
- μ: величина, обратная среднему времени обслуживания (ожидаемое количество последовательных завершений обслуживания за одно и то же время, например, за 30 секунд);
- п: параметр, характеризующий количество клиентов в системе;
- пп: вероятность присутствия п клиенты в системе в устойчивом состоянии.
Далее, пусть Eп представляют количество раз, когда система входит в состояние п, и Lп представляют количество раз, когда система выходит из состояния п. Тогда для всех п, |Eп − Lп| ∈ {0, 1}. То есть количество раз, когда система покидает состояние, отличается не более чем на 1 от количества раз, когда она входит в это состояние, поскольку она либо вернется в это состояние в какой-то момент в будущем (Eп = Lп) или нет (|Eп − Lп| = 1).
Когда система переходит в установившееся состояние, скорость прибытия должна быть равна скорости отправления.
Таким образом, уравнения баланса
подразумевать
Дело в том, что приводит к геометрическое распределение формула
куда
Простая очередь с двумя уравнениями
Распространенная базовая система очередей относится к Erlang, и является модификацией Закон Литтла. Учитывая скорость прибытия λ, процент отсева σ, и скорость вылета μ, длина очереди L определяется как:
Предполагая экспоненциальное распределение ставок, время ожидания W можно определить как долю обслуженных прибывших. Это равно экспоненциальной выживаемости тех, кто не бросает учебу в течение периода ожидания, что дает:
Второе уравнение обычно переписывается как:
Двухэтапная модель одного блока широко распространена в эпидемиологии.[7]
Обзор развития теории
В 1909 г. Агнер Краруп Эрланг, датский инженер, работавший в Копенгагенской телефонной станции, опубликовал первую статью о том, что теперь будет называться теорией очередей.[8][9][10] Он смоделировал количество телефонных звонков, поступающих на АТС, с помощью Пуассоновский процесс и решил Очередь M / D / 1 в 1917 г. и M / D /k в очереди модель 1920 года.[11] В обозначениях Кендалла:
- M означает марковский или без памяти и означает, что прибытие происходит в соответствии с процессом Пуассона;
- D означает детерминированный и означает задания, поступающие в очередь, которые требуют фиксированного объема обслуживания;
- k описывает количество серверов в узле очередности (k = 1, 2, ...).
Если на узле больше заданий, чем серверов, то задания будут стоять в очереди и ждать обслуживания.
Очередь M / G / 1 решена Феликс Поллачек в 1930 г.[12] решение позже преобразовано в вероятностные термины Александр Хинчин и теперь известный как Формула Поллачека – Хинчина.[11][13]
После 1940-х годов теория массового обслуживания стала предметом исследовательского интереса математиков.[13] В 1953 г. Дэвид Джордж Кендалл решил GI / M /k очередь[14] и ввел современное обозначение очередей, теперь известное как Обозначения Кендалла. В 1957 году Поллачек изучил GI / G / 1, используя интегральное уравнение.[15] Джон Кингман дал формулу для среднее время ожидания в Очередь G / G / 1: Формула Кингмана.[16]
Леонард Клейнрок работал над применением теории массового обслуживания к переключение сообщений (в начале 1960-х) и коммутация пакетов (в начале 1970-х). Первым его вкладом в эту область была докторская диссертация в Массачусетский Институт Технологий в 1962 г., опубликована в виде книги в 1964 г. в области коммутации сообщений. Его теоретическая работа, опубликованная в начале 1970-х годов, послужила основой для использования коммутации пакетов в ARPANET, предшественник Интернета.
В матричный геометрический метод и матричные аналитические методы разрешили очереди с фазовый распределенный Следует учитывать распределение времени между прибытиями и обслуживания.[17]
Системы со связанными орбитами являются важной частью теории массового обслуживания в приложениях к беспроводным сетям и обработке сигналов. [18]
Такие проблемы, как показатели производительности для M / G /k очередь остаются открытой проблемой.[11][13]
Сервисные дисциплины

На узлах очередей могут использоваться различные политики планирования:
- Первым пришел-первым вышел
- Также называемый первым прибыл - первым обслужен Эквивалент в русском языке: поздний гость гложет и кость (FCFS),[19] этот принцип гласит, что клиенты обслуживаются по одному и что клиент, который ждал дольше всего, обслуживается первым.[20]
- Последний пришел - первый ушел
- Этот принцип также обслуживает клиентов по одному, но клиент с самым коротким время ожидания будут обслуживаться в первую очередь.[20] Также известен как куча.
- Совместное использование процессора
- Объем услуг распределяется между клиентами поровну.[20]
- Приоритет
- В первую очередь обслуживаются клиенты с высоким приоритетом.[20] Очереди с приоритетом могут быть двух типов: без вытеснения (когда обслуживаемое задание не может быть прервано) и с вытеснением (где обслуживаемое задание может быть прервано заданием с более высоким приоритетом). Никакая работа не теряется ни в одной из моделей.[21]
- Сначала самая короткая работа
- Следующая работа, которую нужно обслужить, - это работа с наименьшим размером
- Первоочередное кратчайшее задание
- Следующее задание, которое нужно обслужить, - это задание с исходным наименьшим размером.[22]
- Наименьшее оставшееся время обработки
- Следующее задание - это задание с наименьшими оставшимися требованиями к обработке.[23]
- Сервисный центр
- Единый сервер: клиенты выстраиваются в очередь, и есть только один сервер
- Несколько параллельных серверов - Единая очередь: клиенты выстраиваются в очередь, есть несколько серверов.
- Несколько серверов - несколько очередей: есть много счетчиков, и клиенты могут решать, куда идти в очередь.
- Ненадежный сервер
Сбои сервера происходят в соответствии со стохастическим процессом (обычно Пуассоном) и сопровождаются периодами настройки, в течение которых сервер недоступен. Прерванный клиент остается в зоне обслуживания до тех пор, пока сервер не будет отремонтирован.[24]
- Ожидание клиента
- Отказ: клиенты решают не вставать в очередь, если она слишком длинная
- Жульничество: клиенты переключаются между очередями, если думают, что благодаря этому их обслужат быстрее
- Возврат: клиенты покидают очередь, если они слишком долго ждали обслуживания
Необслуживаемые прибывающие клиенты (либо из-за того, что очередь не имеет буфера, либо из-за отказа или отказа клиента) также известны как отсевы, а средняя частота отсева является важным параметром, описывающим очередь.
Сети массового обслуживания
Сети очередей - это системы, в которых несколько очередей связаны так называемой маршрутизацией клиентов. Когда клиент обслуживается на одном узле, он может присоединиться к другому узлу и встать в очередь на обслуживание или покинуть сеть.
Для сетей м узлов, состояние системы можно описать м–Мерный вектор (Икс1, Икс2, ..., Иксм) куда Икся представляет количество клиентов на каждом узле.
Простейшая нетривиальная сеть очередей называется тандемные очереди.[25] Первые значительные результаты в этой области были Сети Джексона,[26][27] для чего эффективный стационарное распределение продуктовой формы существует и анализ среднего значения[28] который позволяет вычислять средние показатели, такие как пропускная способность и время пребывания.[29] Если общее количество клиентов в сети остается постоянным, сеть называется закрытой, и было показано, что она имеет стационарное распределение в форме продукта в Теорема Гордона – Ньюэлла.[30] Этот результат был распространен на Сеть BCMP[31] где показано, что сеть с очень общим временем обслуживания, режимами и маршрутизацией клиентов также демонстрирует стационарное распределение в форме продукта. В нормализующая константа можно рассчитать с помощью Алгоритм Бузена, предложенный в 1973 г.[32]
Также были исследованы сети клиентов, Сети Келли где клиенты разных классов имеют разные уровни приоритета на разных узлах обслуживания.[33] Другой тип сети - это G-сети впервые предложено Эрол Геленбе в 1993 г .:[34] эти сети не предполагают экспоненциального распределения времени, как классическая сеть Джексона.
Алгоритмы маршрутизации
В сетях с дискретным временем, где существует ограничение на то, какие узлы обслуживания могут быть активными в любое время, алгоритм планирования с максимальным весом выбирает политику обслуживания, чтобы обеспечить оптимальную пропускную способность в случае, если каждое задание посещает только одного человека. [19] сервисный узел. В более общем случае, когда задания могут посещать более одного узла, маршрутизация противодавления дает оптимальную пропускную способность. А сетевой планировщик должен выбрать алгоритм очередности, что влияет на характеристики более крупной сети[нужна цитата ]. Смотрите также Стохастическое планирование для получения дополнительной информации о диспетчеризации систем массового обслуживания.
Пределы среднего поля
Модели среднего поля рассмотреть предельное поведение эмпирическая мера (доля очередей в разных состояниях) как количество очередей (м выше) уходит в бесконечность. Воздействие других очередей на любую данную очередь в сети аппроксимируется дифференциальным уравнением. Детерминированная модель сходится к тому же стационарному распределению, что и исходная модель.[35]
Приближение интенсивного движения / диффузии
В системе с высокой степенью занятости (загрузка около 1) приближение интенсивного трафика может использоваться для аппроксимации процесса длины очереди с помощью отраженное броуновское движение,[36] Процесс Орнштейна – Уленбека, или более общий диффузионный процесс.[37] Число измерений броуновского процесса равно числу узлов очереди, при этом распространение ограничено неотрицательными ортодоксальный.
Пределы жидкости
Жидкостные модели - это непрерывные детерминированные аналоги сетей массового обслуживания, полученные путем принятия предела, когда процесс масштабируется во времени и пространстве, что позволяет использовать неоднородные объекты. Эта масштабированная траектория сходится к детерминированному уравнению, которое позволяет доказать устойчивость системы. Известно, что сеть массового обслуживания может быть стабильной, но иметь нестабильный предел текучей среды.[38]
Смотрите также
- Модель Эренфеста
- Единица Эрланга
- Сетевое моделирование
- Управление производством проекта
- Зона очереди
- Задержка в очереди
- Система управления очередью
- Практическое правило организации очереди
- Случайное раннее обнаружение
- Теория обновления
- Пропускная способность
- Планирование (вычисление)
- Пробка
- Модель генерации трафика
- Поточная сеть
Рекомендации
- ^ а б c Сундарапандиан, В. (2009). «7. Теория массового обслуживания». Вероятность, статистика и теория массового обслуживания. PHI Learning. ISBN 978-8120338449.
- ^ Лоуренс В. Дауди, Вирджилио А.Ф. Алмейда, Даниэль А. Менассе. «Производительность по дизайну: планирование мощности компьютера на примере».
- ^ Шлехтер, Кира (2 марта 2009 г.). «Медицинский центр Херши откроет переделанное отделение неотложной помощи». Патриот-Новости.
- ^ Мэйхью, Лес; Смит, Дэвид (декабрь 2006 г.). Использование теории очередей для анализа времени завершения работ в отделениях неотложной помощи и неотложной помощи в свете 4-часовой цели правительства. Бизнес-школа Касс. ISBN 978-1-905752-06-5. Получено 2008-05-20.[постоянная мертвая ссылка ]
- ^ Теймс, Х.С., Алгоритмический анализ очередей », глава 9 в« Первом курсе стохастических моделей », Wiley, Chichester, 2003 г.
- ^ Кендалл, Д. (1953). «Случайные процессы, происходящие в теории очередей и их анализ методом вложенной цепи Маркова». Анналы математической статистики. 24 (3): 338–354. Дои:10.1214 / aoms / 1177728975. JSTOR 2236285.
- ^ Эрнандес-Суарес, Карлос (2010). «Применение теории очередей к моделям эпидемий SIS и SEIS». Математика. Biosci. 7 (4): 809–823. Дои:10.3934 / mbe.2010.7.809. PMID 21077709.
- ^ "Агнер Краруп Эрланг (1878-1929) | plus.maths.org". Pass.maths.org.uk. 1997-04-30. Получено 2013-04-22.
- ^ Asmussen, S. R .; Боксма, О. (2009). «От редакции». Системы массового обслуживания. 63 (1–4): 1–2. Дои:10.1007 / s11134-009-9151-8. S2CID 45664707.
- ^ Эрланг, Агнер Краруп (1909). «Теория вероятностей и телефонные разговоры» (PDF). Ныт Тидсскрифт для Matematik B. 20: 33–39. Архивировано из оригинал (PDF) на 2011-10-01.
- ^ а б c Кингман, Дж. Ф. С. (2009). «Первый век Эрланга - и следующий». Системы массового обслуживания. 63 (1–4): 3–4. Дои:10.1007 / s11134-009-9147-4. S2CID 38588726.
- ^ Pollaczek, F., Ueber eine Aufgabe der Wahrscheinlichkeitstheorie, Math. З. 1930 г.
- ^ а б c Уиттл, П. (2002). «Прикладная теория вероятностей в Великобритании». Исследование операций. 50 (1): 227–239. Дои:10.1287 / opre.50.1.227.17792. JSTOR 3088474.
- ^ Кендалл Д.Г. Стохастические процессы, происходящие в теории очередей, и их анализ методом вложенной цепи Маркова, Ann. Математика. Стат. 1953 г.
- ^ Поллачек, Ф., Problèmes Stochastiques posés par le phénomène de education d'une queue
- ^ Кингман, Дж. Ф. С.; Атья (октябрь 1961 г.). «Единая очередь сервера в условиях интенсивного трафика». Математические труды Кембриджского философского общества. 57 (4): 902. Дои:10.1017 / S0305004100036094. JSTOR 2984229.
- ^ Рамасвами, В. (1988). «Стабильная рекурсия для вектора установившегося состояния в марковских цепях типа m / g / 1». Коммуникации в статистике. Стохастические модели. 4: 183–188. Дои:10.1080/15326348808807077.
- ^ Морозов Э. (2017). «Анализ устойчивости многоклассовой повторной системы со связанными орбитальными очередями». Материалы 14-го Европейского семинара. 17: 73–90. Дои:10.1007/978-3-319-66583-2-6 (неактивно 07.11.2020).CS1 maint: DOI неактивен по состоянию на ноябрь 2020 г. (связь)
- ^ а б Мануэль, Лагуна (2011). Моделирование бизнес-процессов, симуляция и дизайн. Pearson Education India. п. 178. ISBN 9788131761359. Получено 6 октября 2017.
- ^ а б c d Пенттинен А., Глава 8 - Системы массового обслуживания, Конспект: S-38.145 - Введение в теорию телетрафика.
- ^ Харчол-Балтер, М. (2012). «Планирование: не вытесняющие, основанные на размере политики». Моделирование производительности и проектирование компьютерных систем. С. 499–507. Дои:10.1017 / CBO9781139226424.039. ISBN 9781139226424.
- ^ Харчол-Балтер, М. (2012). «Планирование: упреждающие, основанные на размере политики». Моделирование производительности и проектирование компьютерных систем. С. 508–517. Дои:10.1017 / CBO9781139226424.040. ISBN 9781139226424.
- ^ Харчол-Балтер, М. (2012). «Планирование: SRPT и справедливость». Моделирование производительности и проектирование компьютерных систем. С. 518–530. Дои:10.1017 / CBO9781139226424.041. ISBN 9781139226424.
- ^ Димитриу, И. (2019). «Мультиклассовая повторная система со связанными орбитами и перерывами в обслуживании: проверка условий стабильности». Работа FRUCT 24. 7: 75–82.
- ^ http://www.stats.ox.ac.uk/~winkel/bs3a07l13-14.pdf#page=4
- ^ Джексон, Дж. Р. (1957). «Сети очередей». Исследование операций. 5 (4): 518–521. Дои:10.1287 / opre.5.4.518. JSTOR 167249.
- ^ Джексон, Джеймс Р. (октябрь 1963 г.). «Системы массового обслуживания, похожие на рабочие места». Наука управления. 10 (1): 131–142. Дои:10.1287 / mnsc.1040.0268. JSTOR 2627213.
- ^ Reiser, M .; Лавенберг, С. С. (1980). "Анализ среднего значения закрытых многоцепочечных сетей массового обслуживания". Журнал ACM. 27 (2): 313. Дои:10.1145/322186.322195. S2CID 8694947.
- ^ Ван Дейк, Н. М. (1993). «О теореме прихода для сетей связи». Компьютерные сети и системы ISDN. 25 (10): 1135–2013. Дои:10.1016 / 0169-7552 (93) 90073-D.
- ^ Гордон, В. Дж .; Ньюэлл, Г.Ф. (1967). «Замкнутые системы массового обслуживания с экспоненциальными серверами». Исследование операций. 15 (2): 254. Дои:10.1287 / opre.15.2.254. JSTOR 168557.
- ^ Baskett, F .; Чанди, К. Мани; Muntz, R.R .; Паласиос, Ф. (1975). «Открытые, закрытые и смешанные сети очередей с разными классами заявок». Журнал ACM. 22 (2): 248–260. Дои:10.1145/321879.321887. S2CID 15204199.
- ^ Бузен, Дж. П. (1973). «Вычислительные алгоритмы для замкнутых сетей массового обслуживания с экспоненциальными серверами» (PDF). Коммуникации ACM. 16 (9): 527–531. Дои:10.1145/362342.362345. S2CID 10702.
- ^ Келли, Ф. (1975). «Сети очередей с разными типами клиентов». Журнал прикладной теории вероятностей. 12 (3): 542–554. Дои:10.2307/3212869. JSTOR 3212869.
- ^ Геленбе, Эрол (Сентябрь 1993 г.). «G-сети с инициированным движением клиентов». Журнал прикладной теории вероятностей. 30 (3): 742–748. Дои:10.2307/3214781. JSTOR 3214781.
- ^ Боббио, А .; Gribaudo, M .; Телек, М. С. (2008). «Анализ крупномасштабных взаимодействующих систем методом среднего поля». 2008 Пятая Международная конференция по количественной оценке систем. п. 215. Дои:10.1109 / QEST.2008.47. ISBN 978-0-7695-3360-5. S2CID 2714909.
- ^ Chen, H .; Уитт, В. (1993). «Диффузионные приближения для открытых сетей массового обслуживания с перерывами в обслуживании». Системы массового обслуживания. 13 (4): 335. Дои:10.1007 / BF01149260. S2CID 1180930.
- ^ Ямада, К. (1995). «Диффузионное приближение для открытых сетей массового обслуживания, зависящих от состояния в условиях интенсивного трафика». Анналы прикладной теории вероятностей. 5 (4): 958–982. Дои:10.1214 / aoap / 1177004602. JSTOR 2245101.
- ^ Брамсон, М. (1999). «Устойчивая сеть массового обслуживания с нестабильной жидкостной моделью». Анналы прикладной теории вероятностей. 9 (3): 818–853. Дои:10.1214 / aoap / 1029962815. JSTOR 2667284.
дальнейшее чтение
- Гросс, Дональд; Карл М. Харрис (1998). Основы теории массового обслуживания. Вайли. ISBN 978-0-471-32812-4. В сети
- Цукерман, Моше. Введение в теорию массового обслуживания и стохастические модели телетрафика (PDF).
- Дейтель, Харви М. (1984) [1982]. Введение в операционные системы (пересмотренное первое издание). Эддисон-Уэсли. п.673. ISBN 978-0-201-14502-1. глава 15, стр. 380–412
- Ньюэлл, Гордрон Ф. (1 июня 1971 г.). Приложения теории массового обслуживания. Чепмен и Холл.
- Леонард Клейнрок, Информационный поток в больших коммуникационных сетях, (Массачусетский технологический институт, Кембридж, 31 мая 1961 г.) Предложение о приеме на степень доктора философии. Тезис
- Леонард Клейнрок. Информационный поток в больших коммуникационных сетях(Ежеквартальный отчет RLE, июль 1961 г.)
- Леонард Клейнрок. Сети связи: стохастический поток сообщений и задержка(Макгроу-Хилл, Нью-Йорк, 1964)
- Клейнрок, Леонард (2 января 1975 г.). Системы массового обслуживания: Том I - Теория. Нью-Йорк: Wiley Interscience. стр.417. ISBN 978-0471491101.
- Клейнрок, Леонард (22 апреля 1976 г.). Системы массового обслуживания: Том II - Компьютерные приложения. Нью-Йорк: Wiley Interscience. стр.576. ISBN 978-0471491118.
- Lazowska, Edward D .; Джон Захоржан; Г. Скотт Грэм; Кеннет С. Севчик (1984). Количественная производительность системы: анализ компьютерной системы с использованием моделей сетей массового обслуживания. Prentice-Hall, Inc. ISBN 978-0-13-746975-8.
внешняя ссылка
Эта статья использование внешняя ссылка может не следовать политикам или рекомендациям Википедии. (Май 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
- Калькулятор теории массового обслуживания
- Учебное пособие и калькуляторы Teknomo по теории массового обслуживания
- Имитация аварийной эвакуации при пожаре в офисе на YouTube
- Курс Virtamo по теории массового обслуживания
- Страница теории массового обслуживания Майрона Хлынки
- Основы теории массового обслуживания
- Бесплатный онлайн-инструмент для решения некоторых классических систем массового обслуживания
- JMT: графическая среда с открытым исходным кодом для теории массового обслуживания
- LINE: универсальный движок для решения моделей очередей
- Что вы больше всего ненавидите в ожидании в очереди: (Дело не в продолжительности ожидания.), Сет Стивенсон, Шифер, 2012 - популярное введение




















