Теория обновления - Renewal theory
Теория обновления это филиал теория вероятности это обобщает Пуассоновский процесс для произвольного времени выдержки. Вместо экспоненциально распределенный время ожидания, процесс продления может иметь любые независимые и одинаково распределенные (IID) времена выдержки с конечным средним значением. Процесс возобновления-вознаграждения дополнительно имеет случайную последовательность вознаграждений, полученных в каждый момент удержания, которые являются IID, но не обязательно должны быть независимыми от времени удержания.
Процесс восстановления обладает асимптотическими свойствами, аналогичными процессу восстановления. сильный закон больших чисел и Центральная предельная теорема. Функция обновления (ожидаемое количество прибывших) и функция вознаграждения (ожидаемая величина вознаграждения) имеют ключевое значение в теории обновления. Функция восстановления удовлетворяет рекурсивному интегральному уравнению, уравнению восстановления. Ключевое уравнение восстановления дает предельное значение свертка из с подходящей неотрицательной функцией. Суперпозицию процессов восстановления можно изучать как частный случай Марковские процессы обновления.
Приложения включают расчет наилучшей стратегии замены изношенного оборудования на заводе и сравнение долгосрочных преимуществ различных страховых полисов. Парадокс проверки связан с тем, что соблюдение интервала обновления во времени т дает интервал со средним значением, превышающим средний интервал обновления.
Процессы продления
Вступление
В процесс обновления является обобщением Пуассоновский процесс. По сути, процесс Пуассона - это марковский процесс с непрерывным временем на положительных целых числах (обычно начинающихся с нуля), которые имеют независимые экспоненциально распределенный время выдержки при каждом целом числе перед переходом к следующему целому числу, . В процессе обновления время ожидания не обязательно должно иметь экспоненциальное распределение; скорее, времена удержания могут иметь любое распределение по положительным числам, при условии, что времена удержания независимы и одинаково распределены (IID ) и имеют конечное среднее.
Формальное определение

Позволять последовательность положительных независимые одинаково распределенные случайные переменные такой, что
Мы говорим о случайной величине как "-я выдержка ».
это ожидание из .
Определите для каждого п > 0 :
каждый называется "время прыжка »и интервалы называются «интервалами обновления».
потом задается случайной величиной
куда это индикаторная функция
представляет количество прыжков, которые произошли за время т, и называется процессом обновления.
Интерпретация
Если рассматривать события, происходящие в случайное время, можно подумать о временах выдержки. как случайное время, прошедшее между двумя последовательными событиями. Например, если в процессе обновления моделируется количество поломок разных машин, то время выдержки представляет собой время между выходом из строя одной машины и выходом из строя другой.
Пуассоновский процесс - это уникальный процесс обновления с Марковская собственность,[1] поскольку экспоненциальное распределение является уникальной непрерывной случайной величиной со свойством без памяти.
Процессы возобновления и вознаграждения
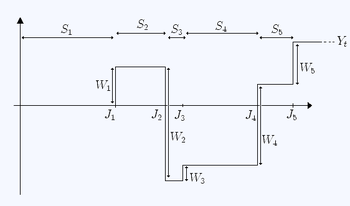
Позволять быть последовательностью IID случайные переменные (награды) удовлетворение
Тогда случайная величина
называется процесс возобновления вознаграждения. Обратите внимание, что в отличие от , каждый может принимать как отрицательные, так и положительные значения.
Случайная величина зависит от двух последовательностей: времени выдержки и награды Эти две последовательности не обязательно должны быть независимыми. Особенно, может быть функцией .
Интерпретация
В контексте вышеупомянутой интерпретации времени ожидания как времени между последовательными сбоями в работе машины "вознаграждения" (которые в данном случае оказываются отрицательными) можно рассматривать как последующие затраты на ремонт, понесенные в результате последовательных неисправностей.
Альтернативная аналогия заключается в том, что у нас есть волшебный гусь, который откладывает яйца с интервалами (временем выдержки), распределенными как . Иногда он откладывает золотые яйца произвольного веса, а иногда - ядовитые яйца (также произвольного веса), которые требуют ответственной (и дорогостоящей) утилизации. "Награды" - последовательные (случайные) финансовые потери / прибыли в результате последовательных яиц (я = 1,2,3, ...) и записывает общую финансовую "награду" т.
Функция продления
Мы определяем функция обновления как ожидаемое значение количества скачков, наблюдаемых до некоторого времени :
Элементарная теорема восстановления
Функция восстановления удовлетворяет
Доказательство В сильный закон больших чисел для процессов обновления подразумевает Чтобы доказать элементарную теорему восстановления, достаточно показать, что равномерно интегрируемо.
Для этого рассмотрим некоторый усеченный процесс обновления, в котором время ожидания определяется как куда это точка такая, что который существует для всех недетерминированных процессов обновления. Этот новый процесс обновления это верхняя граница и его обновления могут происходить только на решетке . Кроме того, количество обновлений в каждый момент времени геометрическое с параметром . Итак, у нас есть
Элементарная теорема восстановления для процессов вознаграждения за обновление
Мы определяем функция вознаграждения:
Функция вознаграждения удовлетворяет
Уравнение обновления
Функция восстановления удовлетворяет
куда - кумулятивная функция распределения и - соответствующая функция плотности вероятности.
Доказательство[2] Мы можем повторить ожидания относительно первого времени выдержки: Из определения процесса обновления, мы имеем
Так
как требуется.
Ключевая теорема восстановления
Позволять Икс быть процессом обновления с функцией обновления и среднее обновление . Позволять быть функцией, удовлетворяющей:
- грамм монотонный и невозрастающий
Ключевая теорема восстановления утверждает, что, поскольку :[3]
Теорема возобновления
Учитывая для любого дает как частный случай теорему восстановления:[4]
- в качестве
Результат может быть доказан с помощью интегральных уравнений или связь аргумент.[5] Хотя это частный случай ключевой теоремы о восстановлении, ее можно использовать для вывода полной теоремы, рассматривая ступенчатые функции и затем увеличивая последовательности ступенчатых функций.[3]
Асимптотические свойства
Процессы обновления и процессы вознаграждения за обновление обладают свойствами, аналогичными свойствам сильный закон больших чисел, которое можно получить из той же теоремы. Если это процесс обновления и это процесс вознаграждения за продление, то:
почти наверняка.
Доказательство Сначала рассмотрим . По определению мы имеем: для всех и так
для всех т ≥ 0.
Теперь, когда у нас есть:
в качестве почти наверняка (с вероятностью 1). Следовательно:
почти наверняка (используя усиленный закон больших чисел); по аналогии:
почти наверняка.
Таким образом (поскольку зажат между двумя терминами)
почти наверняка.[3]
Далее рассмотрим . У нас есть
почти наверняка (используя первый результат и закон больших чисел на ).
Процессы продления дополнительно обладают свойством, аналогичным Центральная предельная теорема:[6]
Парадокс осмотра

Любопытная особенность процессов обновления состоит в том, что если мы подождем некоторое заранее определенное время т а затем посмотрите, насколько велик интервал обновления, содержащий т есть, мы должны ожидать, что он обычно будет больше, чем интервал обновления среднего размера.
Математически парадокс проверки гласит: для любого t> 0 интервал обновления, содержащий t, равен стохастически больше чем первый интервал обновления. То есть для всех Икс > 0 и для всех т > 0:
куда FS - кумулятивная функция распределения времен удержания IID Sя.
Разрешение парадокса состоит в том, что наше выборочное распределение во времени т смещен по размеру, поскольку вероятность выбора интервала пропорциональна его размеру. Однако средний интервал обновления не зависит от размера.
Доказательство Обратите внимание, что время последнего прыжка перед т является ; и что интервал обновления, содержащий т является . потом поскольку оба и больше или равны для всех значений s.
Суперпозиция
Если процесс обновления не является пуассоновским, суперпозиция (сумма) двух независимых процессов обновления не является процессом обновления.[7] Однако такие процессы можно описать в рамках более широкого класса процессов, называемых Марковско-восстановительные процессы.[8] Тем не менее кумулятивная функция распределения первого межсобытийного времени в процессе суперпозиции определяется выражением[9]
куда рk(т) и αk > 0 - это функция распределения времени между событиями и скорость поступления процесса. k.[10]
Пример приложения
Эрик предприниматель п машины, срок эксплуатации каждой из которых равномерно распределен от нуля до двух лет. Эрик может позволить каждой машине поработать до тех пор, пока она не выйдет из строя, при стоимости замены 2600 евро; в качестве альтернативы он может заменить машину в любое время, пока она еще функционирует, по цене 200 евро.
Какова его оптимальная политика замены?
Решение Время жизни п машины можно смоделировать как п независимые параллельные процессы возобновления и вознаграждения, поэтому достаточно рассмотреть случай п = 1. Обозначим этот процесс . Последовательные жизни S заменяющих машин независимы и одинаково распределены, поэтому оптимальная политика одинакова для всех заменяющих машин в процессе. Если Эрик решит в начале жизни машины заменить ее вовремя 0 < т < 2 но машина выходит из строя до этого времени, тогда срок службы S машины равномерно распределена на [0,т] и, следовательно, имеет ожидание 0,5т. Таким образом, общий ожидаемый срок службы машины составляет:
и ожидаемая стоимость W на машину:
Итак, согласно строгому закону больших чисел, его долгосрочная средняя стоимость единицы времени составляет:
затем дифференцируя по т:
это означает, что точки поворота удовлетворяют:
и поэтому
Мы принимаем единственное решение т в [0, 2]: т = 2/3. Это действительно минимум (а не максимум), поскольку стоимость единицы времени стремится к бесконечности как т стремится к нулю, что означает, что стоимость уменьшается по мере т увеличивается до точки 2/3, где она начинает увеличиваться.
Смотрите также
- Теорема Кэмпбелла (вероятность)
- Составной процесс Пуассона
- Марковский процесс с непрерывным временем
- Лемма Литтла
- Теорема Палма – Хинчина
- Пуассоновский процесс
- Теория массового обслуживания
- Остаточное время
- Теория разорения
- Полумарковский процесс
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Июль 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Примечания
- ^ Гриммет и Стирзакер (1992), п. 393.
- ^ Гриммет и Стирзакер (1992), п. 390.
- ^ а б c Гриммет и Стирзакер (1992), п. 395.
- ^ Феллер (1971), п. 347–351.
- ^ Гриммет и Стирзакер (1992), п. 394–5.
- ^ а б Гриммет и Стирзакер (1992), п. 394.
- ^ Гриммет и Стирзакер (1992), п. 405.
- ^ Чинлар, Эрхан (1969). «Теория марковского восстановления». Достижения в прикладной теории вероятностей. Доверие прикладной вероятности. 1 (2): 123–187. Дои:10.2307/1426216. JSTOR 1426216.
- ^ Лоуренс, А. Дж. (1973). «Зависимость интервалов между событиями в процессах суперпозиции». Журнал Королевского статистического общества. Серия B (Методологическая). 35 (2): 306–315. Дои:10.1111 / j.2517-6161.1973.tb00960.x. JSTOR 2984914. формула 4.1
- ^ Чунгмо Фофак, Никайз; Наин, Филипп; Неглия, Джованни; Таусли, Дон. «Анализ сетей кэширования на основе TTL». Труды 6-й Международной конференции по методологиям и инструментам оценки эффективности. Получено 15 ноя, 2012.
Рекомендации
- Кокс, Дэвид (1970). Теория обновления. Лондон: Methuen & Co., стр. 142. ISBN 0-412-20570-X.
- Дуб, Дж. Л. (1948). "Теория обновления с точки зрения теории вероятностей" (PDF). Труды Американского математического общества. 63 (3): 422–438. Дои:10.2307/1990567. JSTOR 1990567.
- Феллер, Уильям (1971). Введение в теорию вероятностей и ее приложения. 2 (второе изд.). Вайли.
- Гримметт, Г.; Стирзакер, Д. Р. (1992). Вероятность и случайные процессы (второе изд.). Издательство Оксфордского университета. ISBN 0198572220.
- Смит, Уолтер Л. (1958). «Теория обновления и ее последствия». Журнал Королевского статистического общества, серия B. 20 (2): 243–302. JSTOR 2983891.
- Ванли Ван, Йоханнес Х. П. Шульц, Вейхуа Дэн и Эли Баркай (2018). «Теория обновления с распределенным временем пребывания с толстыми хвостами: типичное или редкое». Phys. Ред. E. 98 (4): 042139. arXiv:1809.05856. Bibcode:2018PhRvE..98d2139W. Дои:10.1103 / PhysRevE.98.042139.







![{ displaystyle 0 < operatorname {E} [S_ {i}] < infty.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/303b232700cf356843c58010dcd3393627c46153)

![{ displaystyle operatorname {E} [S_ {i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1db907f41c8400d829a1b893df46d20b7d25bbb)



![[J_n, J_ {n + 1}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/817b42a083e1bc24d8215e47b2326c3a50cd86a7)












![{ Displaystyle m (t) = OperatorName {E} [X_ {t}]. ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c55cdd0910db32f06a61d6638c5f1680bcfa8a46)
![{ displaystyle lim _ {t to infty} { frac {1} {t}} m (t) = { frac {1} { operatorname {E} [S_ {1}]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59f16c7b6c9599b43194e1122a8121150858b0e4)
![{ displaystyle lim _ {t to infty} { frac {X_ {t}} {t}} = { frac {1} { operatorname {E} [S_ {1}]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31e47c2a236e95b57ae74176253c46e734003077)








![{ displaystyle { begin {align} { overline {X_ {t}}} & leq sum _ {i = 1} ^ {[at]} operatorname {Geometric} (p) operatorname {E } left [, { overline {X_ {t}}} ^ {2} , right] & leq C_ {1} t + C_ {2} t ^ {2} P left ({ frac {X_ {t}} {t}}> x right) & leq { frac { operatorname {E} left [X_ {t} ^ {2} right]} {t ^ {2} x ^ {2}}} leq { frac { operatorname {E} left [{ overline {X_ {t}}} ^ {2} right]} {t ^ {2} x ^ {2} }} leq { frac {C} {x ^ {2}}}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29c6c48d3d77404c6ada9e0bbc62a6219c76e96b)
![{ displaystyle g (t) = operatorname {E} [Y_ {t}]. ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35d59e7c158d2dd5aab3baf64d637375dda9b1a0)
![{ displaystyle lim _ {t to infty} { frac {1} {t}} g (t) = { frac { operatorname {E} [W_ {1}]} { operatorname {E} [S_ {1}]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94fc2bbcc7f4205c065d3824a46b532a6a141ed1)




![{ displaystyle m (t) = operatorname {E} [X_ {t}] = operatorname {E} [ operatorname {E} (X_ {t} mid S_ {1})]. ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e05d07a9e3171af23fba144fbcb5c2a03ce090b2)
![{ displaystyle operatorname {E} (X_ {t} mid S_ {1} = s) = operatorname { mathbb {I}} _ { {t geq s }} left (1+ operatorname {E} [X_ {ts}] right). ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39464a2eaeb45121361d11d3aba4438b5a0a56a)
![{ displaystyle { begin {align} m (t) & = operatorname {E} [X_ {t}] [12pt] & = operatorname {E} [ operatorname {E} (X_ {t} mid S_ {1})] [12pt] & = int _ {0} ^ { infty} operatorname {E} (X_ {t} mid S_ {1} = s) f_ {S} (s ) , ds [12pt] & = int _ {0} ^ { infty} operatorname { mathbb {I}} _ { {t geq s }} left (1+ operatorname { E} [X_ {ts}] right) f_ {S} (s) , ds [12pt] & = int _ {0} ^ {t} left (1 + m (ts) right) f_ {S} (s) , ds [12pt] & = F_ {S} (t) + int _ {0} ^ {t} m (ts) f_ {S} (s) , ds, конец {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1d1ec955a1a4580e78f07e747ff551c95c9e67f)





![{ Displaystyle г (х) = mathbb {I} _ {[0, ч]} (х)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f9950634ecf29371b59d08ac982251513a7929)



![{ displaystyle lim _ {t to infty} { frac {1} {t}} X_ {t} = { frac {1} { operatorname {E} [S_ {1}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/550b5cf1752eb6ccca0ac9d68570e41b53a22cb9)
![{ displaystyle lim _ {t to infty} { frac {1} {t}} Y_ {t} = { frac {1} { operatorname {E} [S_ {1}]}} operatorname {E} [W_ {1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be5a873d353b5b6397927d08a8de29a6c83fb528)



![{ Displaystyle 0 < OperatorName {E} [S_ {i}] < infty}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91136b7100899241b29332a22ba9019a3fbf9d5d)


![{ displaystyle { frac {J_ {X_ {t}}} {X_ {t}}} = { frac {J_ {n}} {n}} = { frac {1} {n}} sum _ {i = 1} ^ {n} S_ {i} to operatorname {E} [S_ {1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96912bc2a8e290d5a14f2d904657d328c316a303)
![{ displaystyle { frac {J_ {X_ {t} +1}} {X_ {t}}} = { frac {J_ {X_ {t} +1}} {X_ {t} +1}} { frac {X_ {t} +1} {X_ {t}}} = { frac {J_ {n + 1}} {n + 1}} { frac {n + 1} {n}} to operatorname {E} [S_ {1}] cdot 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e51991076c7d41fa573be6ea2d19232d8363ec2b)

![{ displaystyle { frac {1} {t}} X_ {t} to { frac {1} { operatorname {E} [S_ {1}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cac04b5d2c7be16d2921d39a8adb8198cdaf9074)
![{ displaystyle { frac {1} {t}} Y_ {t} = { frac {X_ {t}} {t}} { frac {1} {X_ {t}}} Y_ {t} to { frac {1} { operatorname {E} [S_ {1}]}} cdot operatorname {E} [W_ {1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0bda248d59a2abd99cd0df2a8b3c05bab05cfe5)




![{ displaystyle { begin {align} operatorname {P} (S_ {X_ {t} +1}> x) & {} = int _ {0} ^ { infty} operatorname {P} (S_ { X_ {t} +1}> x mid J_ {X_ {t}} = s) f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ { 0} ^ { infty} operatorname {P} (S_ {X_ {t} +1}> x | S_ {X_ {t} +1}> ts) f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} { frac { operatorname {P} (S_ {X_ {t} +1}> x ,, , S_ {X_ {t} +1}> ts)} { operatorname {P} (S_ {X_ {t} +1}> ts)}} f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} { frac {1-F ( max {x, ts })} {1-F (ts)}} f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} min left {{ frac {1-F (x)} {1-F (ts)}}, { frac {1-F (ts)} {1-F (ts)}} right } f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} = int _ {0} ^ { infty} min left {{ frac {1-F (x)} {1-F (ts)}}, 1 right } f_ {J_ {X_ {t}}} (s) , ds [12pt] & {} geq int _ {0} ^ { infty} (1-F (x)) f_ {J_ {X_ {t}}} (s) , ds = 1-F (x) = operatorname {P} (S_ {1}> x), [12pt] end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca6a13a416b0b4ef32dc077c4bb052983c507097)




![{ displaystyle { begin {align} operatorname {E} [S] & = operatorname {E} [S mid { text {не выполняется до}} t] cdot operatorname {P} [{ text { не сработает до}} t] + operatorname {E} [S mid { text {не сработает до}} t] cdot operatorname {P} [{ text {не сработает до}} t] [6pt] & = 0,5t ({ frac {t} {2}}) + t ({ frac {2-t} {2}}) end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8e0739e112060763178a0e31b789d8100fca8e5)
![{ displaystyle { begin {align} operatorname {E} [W] & = operatorname {E} [W mid { text {не выполняется до}} t] cdot operatorname {P} ({ text { терпит неудачу до}} t) + operatorname {E} [W mid { text {не терпит неудачу раньше}} t] cdot operatorname {P} ({ text {не терпит неудачу раньше}} t) [6pt] & = 2600 ({ frac {t} {2}}) + 200 ({ frac {2-t} {2}}) = 1200t + 200. End {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/085216b522dfbf33cb3fc71290697b12503962a8)
![{ displaystyle { frac {1} {t}} Y_ {t} simeq { frac { operatorname {E} [W]} { operatorname {E} [S]}} = { frac {4 ( 1200t + 200)} {t ^ {2} + 4t-2t ^ {2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1fb2305b9678f98f546ae389c2f277163434afd)

![{ displaystyle { begin {align} 0 & = (4t-t ^ {2}) (1200) - (4-2t) (1200t + 200) = 4800t-1200t ^ {2} -4800t-800 + 2400t ^ { 2} + 400t [6pt] & = - 800 + 400t + 1200t ^ {2}, end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79ab7f68475f7573e4e243232e03af08b09d5845)
