Эффект Зеемана - Zeeman effect
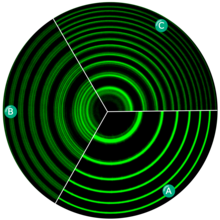
В Эффект Зеемана (/ˈzeɪмən/; Голландское произношение: [ˈZeːmɑn]), названный в честь нидерландский язык физик Питер Зееман, - эффект расщепления спектральная линия на несколько компонентов при наличии статического магнитное поле. Это аналог Эффект Старка, расщепление спектральной линии на несколько составляющих при наличии электрическое поле. Также аналогично эффекту Штарка, переходы между различными компонентами, как правило, имеют разную интенсивность, причем некоторые из них полностью запрещены (в диполь приближение), как регулируется правила отбора.
Поскольку расстояние между подуровнями Зеемана является функцией напряженности магнитного поля, этот эффект можно использовать для измерения напряженности магнитного поля, например что из солнце и другие звезды или в лаборатории плазма.Эффект Зеемана очень важен в таких приложениях, как ядерный магнитный резонанс спектроскопия, электронный спиновой резонанс спектроскопия, магнитно-резонансная томография (МРТ) и Мессбауэровская спектроскопия. Его также можно использовать для повышения точности атомно-абсорбционная спектроскопия Теория о магнитное чувство птиц предполагает, что белок в сетчатке глаза изменен из-за эффекта Зеемана.[1]
Когда спектральные линии являются линиями поглощения, эффект называется обратный эффект Зеемана.
Номенклатура
Исторически различают нормальный и аномальный эффект Зеемана (обнаружено Томас Престон в Дублине, Ирландия[2]). Аномальный эффект проявляется на переходах, где сетка вращение из электроны не равно нулю. Он был назван «аномальным», потому что спин электрона еще не был обнаружен, и поэтому ему не было хорошего объяснения в то время, когда Зееман наблюдал эффект.
При более высокой напряженности магнитного поля эффект перестает быть линейным. При еще более высокой напряженности поля, когда сила внешнего поля сравнима с силой внутреннего поля атома, электронная связь нарушается и спектральные линии меняются. Это называется Эффект Пашена-Бека.
В современной научной литературе эти термины используются редко, чаще всего используется только «эффект Зеемана».
Теоретическая презентация
Общая Гамильтониан атома в магнитном поле
где - невозмущенный гамильтониан атома, а это возмущение из-за магнитного поля:
где это магнитный момент атома. Магнитный момент состоит из электронной и ядерной частей; однако последний на много порядков меньше и здесь не будет учитываться. Следовательно,
где это Магнетон Бора, это полный электронный угловой момент, и это G-фактор Ланде Более точный подход состоит в том, чтобы учесть, что оператор магнитного момента электрона представляет собой сумму вкладов орбитальный угловой момент и спиновый угловой момент , где каждое умножается на соответствующий гиромагнитное отношение:
где и (последний называется аномальное гиромагнитное отношение; отклонение значения от 2 связано с влиянием квантовая электродинамика ). В случае LS муфта, можно просуммировать по всем электронам в атоме:
где и - полный орбитальный момент и спин атома, а усреднение проводится по состоянию с заданным значением полного углового момента.
Если срок взаимодействия маленький (меньше тонкая структура ), это можно рассматривать как возмущение; это собственно эффект Зеемана. В эффекте Пашена – Бэка, описанном ниже, превышает LS муфта значительно (но все еще мало по сравнению с ). В сверхсильных магнитных полях взаимодействие магнитного поля может превышать , в этом случае атом больше не может существовать в его обычном смысле, и говорят о Уровни Ландау вместо. Есть промежуточные случаи, которые сложнее этих предельных случаев.
Слабое поле (эффект Зеемана)
Если спин-орбитальное взаимодействие преобладает над действием внешнего магнитного поля, и отдельно не сохраняются, только полный угловой момент является. Векторы спинового и орбитального углового момента можно рассматривать как прецессирующие относительно (фиксированного) вектора полного углового момента . «Усредненный» вектор спина (время -) тогда является проекцией спина на направление :
а для «усредненного» орбитального вектора (время -):
Таким образом,
С помощью и возводя обе стороны в квадрат, получаем
и: используя и возводя обе стороны в квадрат, получаем
Совмещая все и взяв , получаем магнитную потенциальную энергию атома в приложенном внешнем магнитном поле,
где величина в квадратных скобках - это G-фактор Ланде граммJ атома ( и ) и - z-компонента полного углового момента. Для одиночного электрона над заполненными оболочками и , g-фактор Ланде можно упростить до:
Принимая чтобы быть возмущением, поправка Зеемана к энергии равна
Пример: переход Лаймана-альфа в водороде
В Лайман-альфа переход в водород в присутствии спин-орбитальное взаимодействие включает переходы
- и
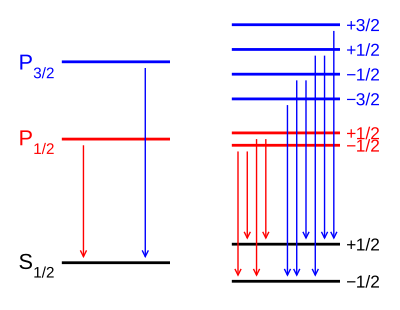
В присутствии внешнего магнитного поля эффект Зеемана в слабом поле расщепляет 1S1/2 и 2P1/2 уровней в 2 состояния каждый () и 2P3/2 уровень на 4 состояния (). G-факторы Ланде для трех уровней:
- за (j = 1/2, l = 0)
- за (j = 1/2, l = 1)
- за (j = 3/2, l = 1).
В частности, обратите внимание, что величина энергетического расщепления различна для разных орбиталей, поскольку gJ значения разные. Слева изображено расщепление тонкой структуры. Это расщепление происходит даже в отсутствие магнитного поля, так как оно обусловлено спин-орбитальной связью. Справа изображено дополнительное зеемановское расщепление, возникающее при наличии магнитных полей.
| Начальное состояние () | Конечное состояние () | Возмущение энергии |
|---|---|---|
Сильное поле (эффект Пашена – Бэка)
Эффект Пашена – Бака - это расщепление уровней энергии атомов в присутствии сильного магнитного поля. Это происходит, когда внешнее магнитное поле достаточно сильное, чтобы нарушить связь между орбитальными () и вращать () угловые моменты. Этот эффект является пределом сильного поля эффекта Зеемана. Когда , эти два эффекта эквивалентны. Эффект назван в честь Немецкий физики Фридрих Пашен и Эрнст Э. А. Бэк.[3]
Когда возмущение магнитного поля значительно превышает спин-орбитальное взаимодействие, можно смело предположить . Это позволяет получить ожидаемые значения и быть легко оцененным для состояния . Энергии просто
Вышесказанное может быть истолковано как подразумевающее, что LS-связь полностью нарушена внешним полем. Однако и все еще «хорошие» квантовые числа. Вместе с правила отбора для электрический дипольный переход, т.е. это позволяет вообще игнорировать степень свободы спина. В результате будут видны только три спектральные линии, соответствующие правило выбора. Расщепление является независимый невозмущенных энергий и электронных конфигураций рассматриваемых уровней. В целом (если ), эти три компонента фактически представляют собой группы из нескольких переходов в каждой из-за остаточного спин-орбитального взаимодействия.
В общем, теперь необходимо добавить спин-орбитальную связь и релятивистские поправки (которые имеют тот же порядок, известный как «тонкая структура») как возмущение этих «невозмущенных» уровней. Теория возмущений первого порядка с этими поправками на тонкую структуру дает следующую формулу для атома водорода в пределе Пашена – Бака:[4]
| Начальное состояние () | Начальное возмущение энергии | Конечное состояние () |
|---|---|---|
Промежуточное поле для j = 1/2
В приближении магнитного диполя гамильтониан, включающий как сверхтонкий и взаимодействия Зеемана
где - сверхтонкое расщепление (в Гц) при нулевом приложенном магнитном поле, и являются Магнетон Бора и ядерный магнетон соответственно, и - операторы углового момента электрона и ядра; это G-фактор Ланде:
- .
В случае слабых магнитных полей зеемановское взаимодействие можно рассматривать как возмущение основание. В режиме сильного поля магнитное поле становится настолько сильным, что эффект Зеемана будет преобладать, и необходимо использовать более полную основу или просто поскольку и будет постоянным в пределах данного уровня.
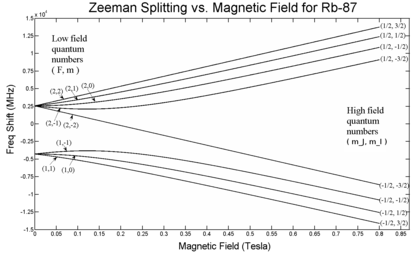
Чтобы получить полную картину, включая промежуточные значения напряженности поля, мы должны рассмотреть собственные состояния, которые являются суперпозициями и основные состояния. За , гамильтониан может быть решен аналитически, что приводит к формуле Брейта-Раби. Примечательно, что электрическое квадрупольное взаимодействие равно нулю при (), так что эта формула довольно точна.
Теперь мы используем квантово-механическую лестничные операторы, которые определены для общего оператора углового момента так как
Эти лестничные операторы обладают свойством
так долго как лежит в диапазоне (в противном случае они возвращают ноль). Использование лестничных операторов и Мы можем переписать гамильтониан как
Теперь мы видим, что в любой момент проекция полного углового момента будут сохранены. Это потому, что оба и покинуть штаты с определенными и без изменений, а и либо увеличить и уменьшить или наоборот, поэтому сумма всегда остается неизменной. Кроме того, поскольку есть только два возможных значения которые . Следовательно, для каждого значения есть только два возможных состояния, и мы можем определить их как основу:
Эта пара состояний является Двухуровневая квантово-механическая система. Теперь мы можем определить матричные элементы гамильтониана:
Решая собственные значения этой матрицы (как это можно сделать вручную - см. Двухуровневая квантово-механическая система или, что проще, с помощью системы компьютерной алгебры) мы приходим к сдвигам энергии:
где - это расщепление (в Гц) между двумя сверхтонкими подуровнями в отсутствие магнитного поля , называется параметром напряженности поля (Примечание: для выражение под квадратным корнем является точным квадратом, поэтому последний член следует заменить на ). Это уравнение известно как Формула Брейта-Раби и полезен для систем с одним валентным электроном в () уровень.[5][6]
Обратите внимание, что index в следует рассматривать не как полный угловой момент атома, а как асимптотический полный угловой момент. Он равен полному угловому моменту, только если в противном случае собственные векторы, соответствующие различным собственным значениям гамильтониана, являются суперпозициями состояний с разными но равный (за исключением ).
Приложения
Астрофизика

Джордж Эллери Хейл был первым, кто заметил эффект Зеемана в спектрах Солнца, указывающий на существование сильных магнитных полей в солнечных пятнах. Такие поля могут быть довольно большими, порядка 0,1 тесла или выше. Сегодня эффект Зеемана используется для получения магнитограммы показывает изменение магнитного поля на Солнце.
Лазерное охлаждение
Эффект Зеемана используется во многих лазерное охлаждение такие приложения, как магнитооптическая ловушка и Зееман медленнее.
Связь спиновых и орбитальных движений, опосредованная зеемановской энергией
Спин-орбитальное взаимодействие в кристаллах обычно связывают с взаимодействием матриц Паули. к импульсу электрона которое существует даже в отсутствие магнитного поля . Однако в условиях эффекта Зеемана, когда , аналогичного взаимодействия можно добиться, связав к электронной координате через пространственно неоднородный гамильтониан Зеемана
- ,
где тензорный Ланде грамм-фактор и либо или , или оба они зависят от координаты электрона . Такие -зависимый гамильтониан Зеемана пары электронного спина оператору представляющий орбитальное движение электрона. Неоднородное поле может быть как гладким полем внешних источников, так и быстроосциллирующим микроскопическим магнитным полем в антиферромагнетиках.[7] Спин-орбитальная связь через макроскопически неоднородное поле наномагнетиков используется для электрического управления электронными спинами в квантовых точках через электрический дипольный спиновой резонанс,[8] и движение спинов электрическим полем из-за неоднородной был также продемонстрирован.[9]
Смотрите также
- Магнитооптический эффект Керра
- Эффект Фойгта
- Эффект Фарадея
- Эффект хлопка-мутона
- Поляризационная спектроскопия
- Zeeman Energy
- Эффект Старка
- Баранина сдвиг
- Электронная конфигурация говорит, что в подоболочке p (l = 1) имеется 3 уровня энергии ml = -1,0,1, но мы видим только два p1 / 2 и p3 / 2. для подоболочки s (l = 0) имеется только 1 энергетический уровень (ml = 0), но здесь мы имеем 2. l, соответствующий тонкой структуре, ml, соответствующий сверхтонкой структуре.
Рекомендации
- ^ Талау, Питер; Ритц, Торстен; Бурда, Хайнек; Wegner, Regina E .; Вильчко, Росвита (18 апреля 2006 г.). «Механизмы магнитного компаса птиц и грызунов основаны на разных физических принципах». Журнал интерфейса Королевского общества. 3 (9): 583–587. Дои:10.1098 / rsif.2006.0130. ЧВК 1664646. PMID 16849254.
- ^ Престон, Томас (1898). «Радиационные явления в сильном магнитном поле». Научные труды Королевского Дублинского общества. 2-я серия. 6: 385–342.
- ^ Paschen, F .; Бэк, Э. (1921). "Liniengruppen magnetisch vervollständigt" [группы линий, завершенные магнитным полем [т.е. полностью разрешенные]]. Physica (на немецком). 1: 261–273. Доступны на: Лейденский университет (Нидерланды)
- ^ Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Prentice Hall. п. 247. ISBN 0-13-111892-7. OCLC 40251748.
- ^ Вудгейт, Гордон Кембл (1980). Элементарная атомная структура (2-е изд.). Оксфорд, Англия: Издательство Оксфордского университета. С. 193–194.
- ^ Впервые появился в: Breit, G .; Раби, И. (1931). «Измерение ядерного спина». Физический обзор. 38 (11): 2082–2083. Bibcode:1931ПхРв ... 38.2082Б. Дои:10.1103 / PhysRev.38.2082.2.
- ^ Пекар С. И., Рашба Э. И. Комбинированный резонанс в кристаллах в неоднородных магнитных полях. Phys. - ЖЭТФ 20, 1295 (1965) http://www.jetp.ac.ru/cgi-bin/dn/e_020_05_1295.pdf
- ^ Y. Tokura, W. G. van der Wiel, T. Obata, S. Tarucha, Когерентное управление спином одного электрона в наклонном зеемановском поле, Phys. Rev. Lett. 96, 047202 (2006)
- ^ Салис Г., Като Ю., Энслин К., Дрисколл, округ Колумбия, Госсард А.С., Авшалом Д.Д. (2001). «Электрический контроль спиновой когерентности в полупроводниковых наноструктурах». Природа. 414 (6864): 619–622. Дои:10.1038 / 414619a. PMID 11740554. S2CID 4393582.CS1 maint: использует параметр авторов (ссылка на сайт)
Исторический
- Condon, E. U .; Г. Х. Шортли (1935). Теория атомных спектров. Издательство Кембриджского университета. ISBN 0-521-09209-4. (В главе 16 дается всестороннее описание по состоянию на 1935 год.)
- Зееман, П. (1896). "Over de invloed eener magnetisatie op den aard van het door een stof uitgezonden licht" [О влиянии магнетизма на природу света, излучаемого веществом]. Verslagen van de Gewone Vergaderingen der Wisen Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Отчеты обычных сессий математической и физической секции (Королевская академия наук в Амстердаме)] (на голландском). 5: 181–184 и 242–248.
- Зееман, П. (1897). «О влиянии магнетизма на природу света, излучаемого веществом». Философский журнал. 5-я серия. 43 (262): 226–239. Дои:10.1080/14786449708620985.
- Зееман, П. (11 февраля 1897 г.). «Влияние намагничивания на природу света, излучаемого веществом». Природа. 55 (1424): 347. Bibcode:1897Натура..55..347Z. Дои:10.1038 / 055347a0.
- Зееман, П. (1897). "Более двойное и тройное в широком спектре, teweeggebracht door uitwendige magnetische krachten" [О дублетах и триплетах в спектре, вызванных внешними магнитными силами]. Verslagen van de Gewone Vergaderingen der Wisen Natuurkundige Afdeeling (Koninklijk Akademie van Wetenschappen te Amsterdam) [Отчеты обычных сессий математической и физической секции (Королевская академия наук в Амстердаме)] (на голландском). 6: 13–18, 99–102 и 260–262.
- Зееман, П. (1897). «Дублеты и триплеты в спектре, создаваемые внешними магнитными силами». Философский журнал. 5-я серия. 44 (266): 55–60. Дои:10.1080/14786449708621028.
Современное
- Фейнман, Ричард П., Лейтон, Роберт Б., Пески, Мэтью (1965). Лекции Фейнмана по физике. 3. Эддисон-Уэсли. ISBN 0-201-02115-3.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- Форман, Пол (1970). «Альфред Ланде и аномальный эффект Зеемана, 1919-1921». Исторические исследования в физических науках. 2: 153–261. Дои:10.2307/27757307. JSTOR 27757307.
- Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Prentice Hall. ISBN 0-13-805326-X.
- Либофф, Ричард Л. (2002). Введение в квантовую механику. Эддисон-Уэсли. ISBN 0-8053-8714-5.
- Собельман, Игорь И. (2006). Теория атомных спектров. Альфа-наука. ISBN 1-84265-203-6.
- Фут, К. Дж. (2005). Атомная физика. ISBN 0-19-850696-1.


























![vec S cdot vec J = frac {1} {2} (J ^ 2 + S ^ 2 - L ^ 2) = frac { hbar ^ 2} {2} [j (j + 1) - l (l + 1) + s (s + 1)],](https://wikimedia.org/api/rest_v1/media/math/render/svg/26e9f5a54c934ff91a0ee2e1e0711656fc8a5110)

![vec L cdot vec J = frac {1} {2} (J ^ 2 - S ^ 2 + L ^ 2) = frac { hbar ^ 2} {2} [j (j + 1) + l (l + 1) - s (s + 1)].](https://wikimedia.org/api/rest_v1/media/math/render/svg/394b91804fd17c811c0003f1d0ea096d640f39b7)

![{ displaystyle { begin {align} V _ { rm {M}} & = mu _ { rm {B}} Bm_ {j} left [g_ {L} { frac {j (j + 1) + l (l + 1) -s (s + 1)} {2j (j + 1)}} + g_ {S} { frac {j (j + 1) -l (l + 1) + s (s +1)} {2j (j + 1)}} right] & = mu _ { rm {B}} Bm_ {j} left [1+ (g_ {S} -1) { frac {j (j + 1) -l (l + 1) + s (s + 1)} {2j (j + 1)}} right], & = mu _ { rm {B}} Bm_ {j} g_ {j} end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/213add165a96705cd8e71d5cae67f97afa873ced)































![[H_ {0}, S] = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/c381cfc71af43948523f8c7d1a9fc9d2c8246665)










![{ Displaystyle E_ {z + fs} = E_ {z} + { frac {m_ {e} c ^ {2} alpha ^ {4}} {2n ^ {3}}} left {{ frac {3} {4n}} - left [{ frac {l (l + 1) -m_ {l} m_ {s}} {l (l + 1/2) (l + 1)}} right] верно}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba7927da53bd8a30b0213965a2a7cad81d83e9c5)






































































