Климатическая модель - Climate model

Климатические модели - это системы дифференциальные уравнения основанный на основных законах физика, движение жидкости, и химия. Чтобы «запустить» модель, ученые делят планету на трехмерную сетку, применяют основные уравнения и оценивают результаты. Атмосферные модели рассчитывают ветры, теплопередача, радиация, относительная влажность, и поверхность гидрология внутри каждой сетки и оцените взаимодействие с соседними точками.

Числовой климатические модели использовать количественные методы для моделирования взаимодействия важных факторов климата, в том числе атмосфера, океаны, поверхности суши и лед. Они используются для самых разных целей: от изучения динамики климатической системы до прогнозов будущего. климат. Климатические модели также могут быть качественными (т.е. не численными) моделями, а также описательными, в значительной степени описательными, возможного будущего.^[1]

Количественные климатические модели учитывают поступающие энергия от солнца короткой волной электромагнитное излучение, в основном видимый и коротковолновый (ближний) инфракрасный, а также исходящие длинные волны (дальние) инфракрасный электромагнитный. Любой дисбаланс приводит к изменение температуры.

Количественные модели различаются по сложности:

• Просто лучистое тепло модель передачи рассматривает землю как единую точку и усредняет исходящую энергию
• Его можно расширить по вертикали (радиационно-конвективные модели) и / или по горизонтали.
• Наконец, (связанная) атмосфера – океан–морской лед глобальные климатические модели решить полные уравнения для массы и передача энергии и лучистый обмен.
• Другие типы моделирования могут быть взаимосвязаны, например землепользование, в Модели системы Земля, что позволяет исследователям прогнозировать взаимодействие между климатом и экосистемы.

Коробочные модели

Схема простой модели коробки, используемой для иллюстрации потоки в геохимических циклах, показывая источник (Q), тонуть (S) и резервуар (М)

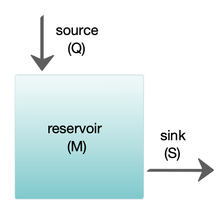
Коробчатые модели - это упрощенные версии сложных систем, сводящие их к коробкам (или резервуары ) связаны потоками. Предполагается, что ящики перемешаны однородно. Внутри данного ящика концентрация любых химические вещества поэтому единообразно. Однако численность вида в пределах данного ящика может варьироваться в зависимости от времени из-за поступления в ящик (или потери из него) или из-за производства, потребления или разложения этого вида внутри ящика.

Простые ящичные модели, то есть ящичковая модель с небольшим количеством ящиков, свойства которых (например, их объем) не меняются со временем, часто полезны для вывода аналитических формул, описывающих динамику и постоянную численность вида. Более сложные ящичные модели обычно решаются с использованием численных методов.

Коробчатые модели широко используются для моделирования экологических систем или экосистем и в исследованиях циркуляция океана и цикл углерода.^[2]Они являются экземплярами многокамерная модель.

Нульмерные модели

Очень простая модель радиационное равновесие Земли

${ displaystyle (1-a) S pi r ^ {2} = 4 pi r ^ {2} epsilon sigma T ^ {4}}$

где

• левая часть представляет собой поступающую энергию от Солнца
• правая часть представляет собой исходящую от Земли энергию, рассчитанную из Закон Стефана-Больцмана предполагая модельную фиктивную температуру, Т, иногда называемая "равновесной температурой Земли", то есть

и

• S это солнечная постоянная - приходящая солнечная радиация на единицу площади - около 1367 Вт · м⁻²
• ${ displaystyle a}$ это Земля в среднем альбедо, измеряется как 0,3.^[3][4]
• р радиус Земли - примерно 6,371 × 10⁶м
• π математическая константа (3.141 ...)
• ${ displaystyle sigma}$ это Постоянная Стефана-Больцмана —Приблизительно 5,67 × 10⁻⁸ Дж · К⁻⁴· М⁻²· С⁻¹
• ${ displaystyle epsilon}$ эффективный излучательная способность земли, около 0,612

Постоянная πr² можно исключить, давая

${ Displaystyle (1-а) S = 4 epsilon sigma T ^ {4}}$

Решая температуру,

${ displaystyle T = { sqrt [{4}] { frac {(1-a) S} {4 epsilon sigma}}}}$

Это дает кажущуюся эффективную среднюю температуру земли 288K (15 ° C; 59 ° F ).^[5] Это потому, что приведенное выше уравнение представляет собой эффективное радиационный температура Земли (включая облака и атмосферу).

Эта очень простая модель весьма поучительна. Например, он легко определяет влияние на среднюю температуру Земли изменений солнечной постоянной или изменения альбедо или эффективной излучательной способности Земли.

Средний коэффициент излучения Земли легко оценить по имеющимся данным. Коэффициенты излучения земных поверхностей находятся в диапазоне от 0,96 до 0,99.^[6][7] (за исключением некоторых небольших пустынных районов, которые могут быть всего 0,7). Однако облака, которые покрывают примерно половину поверхности Земли, имеют средний коэффициент излучения около 0,5.^[8] (которая должна быть уменьшена в четвертой степени отношения абсолютной температуры облака к средней абсолютной температуре Земли) и средней температуры облака около 258 К (-15 ° C; 5 ° F).^[9] Если учесть все это должным образом, эффективный коэффициент излучения Земли составляет около 0,64 (средняя температура Земли 285 K (12 ° C; 53 ° F)).

Эта простая модель легко определяет влияние изменений солнечной мощности или изменения альбедо Земли или эффективного коэффициента излучения Земли на среднюю температуру Земли. Однако в нем ничего не говорится о том, что могло бы заставить эти вещи измениться. Модели с нулевой размерностью не учитывают распределение температуры на Земле или факторы, перемещающие энергию по Земле.

Радиационно-конвективные модели

Приведенная выше нульмерная модель, использующая солнечную постоянную и заданную среднюю температуру Земли, определяет эффективную излучательную способность Земли длинноволновой радиации, излучаемой в космос. По вертикали это можно уточнить в одномерной радиационно-конвективной модели, которая рассматривает два процесса переноса энергии:

• Апвеллинг и нисходящий перенос излучения через слои атмосферы, которые поглощают и излучают инфракрасное излучение
• восходящий перенос тепла конвекцией (особенно важно в нижних тропосфера ).

Радиационно-конвективные модели имеют преимущества по сравнению с простой моделью: они могут определять эффекты изменения парниковый газ концентрации на эффективную излучательную способность и, следовательно, температуру поверхности. Но необходимы дополнительные параметры для определения локальной излучательной способности и альбедо и учета факторов, перемещающих энергию вокруг Земли.

Влияние обратной связи лед-альбедо на глобальную чувствительность в одномерной радиационно-конвективной модели климата.^[10][11][12]

Модели более высокого измерения

Нульмерную модель можно расширить, чтобы учесть энергию, переносимую горизонтально в атмосфере. Такая модель вполне может быть зонально в среднем. Эта модель имеет то преимущество, что допускает рациональную зависимость местного альбедо и излучательной способности от температуры - полюса могут быть ледяными, а экватор - теплыми, но отсутствие истинной динамики означает, что необходимо указать горизонтальный перенос.^[13]

EMIC (модели земных систем средней сложности)

В зависимости от природы задаваемых вопросов и подходящих временных масштабов существуют, с одной стороны, концептуальные, более индуктивные модели, а с другой стороны, модели общей циркуляции работает с максимально возможным пространственным и временным разрешением. Модели средней сложности ликвидируют разрыв. Одним из примеров является модель Climber-3. Его атмосфера представляет собой 2,5-мерную статистико-динамическую модель с разрешением 7,5 ° × 22,5 ° и временным шагом в полдня; океан - МОМ-3 (Модульная модель океана ) с сеткой 3,75 ° × 3,75 ° и 24 уровнями по вертикали.^[14]

GCM (глобальные климатические модели или модели общей циркуляции)

Общие модели циркуляции (GCM) дискретизируют уравнения движения жидкости и передачи энергии и интегрируют их с течением времени. В отличие от более простых моделей, GCM разделяют атмосферу и / или океаны на сетки дискретных «ячеек», которые представляют собой вычислительные единицы. В отличие от более простых моделей, которые делают предположения о смешивании, внутренние процессы ячейки, такие как конвекция, которые происходят в слишком малых масштабах, чтобы их можно было разрешить напрямую, параметризуются на уровне ячейки, тогда как другие функции управляют интерфейсом между ячейками.

Атмосферные GCM (AGCM) моделируют атмосферу и накладывают температура поверхности моря как граничные условия. Связанные ГЦМ атмосфера-океан (МОЦАО, например HadCM3, EdGCM, GFDL CM2.X, ARPEGE-Climat)^[15] объединить две модели. Первая модель климата общей циркуляции, сочетающая в себе океанические и атмосферные процессы, была разработана в конце 1960-х гг. NOAA Лаборатория геофизической гидродинамики^[16] МОЦАО представляют собой вершину сложности климатических моделей и учитывают как можно больше процессов. Однако они все еще находятся в стадии разработки, и остается неопределенность. Они могут быть связаны с моделями других процессов, такими как цикл углерода, чтобы лучше моделировать эффекты обратной связи. Такие интегрированные мультисистемные модели иногда называют либо «моделями земной системы», либо «моделями глобального климата».

Исследования и разработки

Существует три основных типа институтов, в которых разрабатываются, внедряются и используются климатические модели:

• Национальные метеорологические службы. Большинство национальных метеорологических служб имеют климатология раздел.
• Университеты. Соответствующие кафедры включают атмосферные науки, метеорологию, климатологию и географию.
• Национальные и международные исследовательские лаборатории. Примеры включают Национальный центр атмосферных исследований (NCAR, в Боулдер, Колорадо, США), Лаборатория геофизической гидродинамики (GFDL, в Принстон, Нью-Джерси, СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ), Лос-Аламосская национальная лаборатория, то Центр климатических предсказаний и исследований Хэдли (в Эксетер, Великобритания), Институт метеорологии Макса Планка в Гамбурге, Германия, или Лаборатория науки о климате и окружающей среде (LSCE), Франция, и это лишь некоторые из них.

В Всемирная программа исследования климата (ВПИК), организованный Всемирная метеорологическая организация (ВМО) координирует исследовательскую деятельность по моделированию климата во всем мире.

2012 год Национальный исследовательский совет США В отчете обсуждалось, как крупное и разнообразное предприятие по моделированию климата в США могло бы развиться и стать более унифицированным.^[17] В отчете говорится, что повышения эффективности можно добиться, разработав общую программную инфраструктуру, разделяемую всеми исследователями климата США, и проведя ежегодный форум по моделированию климата.^[18]

Смотрите также

• Атмосферный реанализ
• Модель общей циркуляции
• Измерение атмосферной радиации (ARM) (в США)
• Climateprediction.net
• GFDL CM2.X
• GO-ESSP
• Численный прогноз погоды
• Статическая модель атмосферы
• Модель прогнозирования тропических циклонов
• Проверка и валидация компьютерных имитационных моделей
• Модель морского льда CICE

Климатические модели в сети

• Dapper / DChart - построить и загрузить данные модели, на которые ссылается Четвертый отчет об оценке (AR4) Межправительственная комиссия по изменению климата. (Больше недоступно)
• Модель климатической системы сообщества NCAR / UCAR (CCSM)
• Прогноз климата своими руками
• Первичные исследования GCM, разработанные NASA / GISS (Институт космических исследований Годдарда)
• Оригинальная глобальная климатическая модель NASA / GISS (GCM) с удобным интерфейсом для ПК и Mac
• Информация о модели CCCma и интерфейс для получения данных модели
• NOAA / Лаборатория геофизической гидродинамики CM2 информация о глобальной климатической модели и файлы выходных данных модели
• Сухой идеализированный AGCM на основе вышеуказанного GFDL CM2^[19]
• Модель идеализированной влажной атмосферы (MiMA): на основе GFDL CM2. Сложность между сухими моделями и полными GCM^[20]
• Глобальная климатическая модель Университета Виктории, бесплатно для скачивания. Ведущий исследователь был автором МГЭИК доклад об изменении климата.
• vimeo.com/user12523377/videos Визуализации климатических моделей ETH Zurich
• Эмпирическая климатическая модель

использованная литература

Список используемой литературы

• Роулстон, Ян; Норбери, Джон (2013). Невидимый во время бури: роль математики в понимании погоды. Издательство Принстонского университета.

внешние ссылки

• Проект взаимного сравнения связанных моделей
• О радиационной и динамической обратной связи над экваториальным тихоокеанским холодным языком
• Основные радиационные расчеты - Открытие глобального потепления
• Хендерсон-Селлерс, А .; Робинсон, П. Дж. (1999). Современная климатология. Нью-Йорк: Лонгман. ISBN  978-0-582-27631-4. Архивировано из оригинал 28 сентября 2007 г.
• Веб-сайт Climate Modeling 101 посредством Национальный исследовательский совет США - Этот сайт знакомит с принципами работы климатических моделей. Информация основана на экспертных консенсусных отчетах Национальный исследовательский совет США Совет по атмосферным наукам и климату. Самая последняя Национальная стратегия развития климатического моделирования.
• Почему важны результаты климатических моделей следующего поколения CarbonBrief, гостевой пост Белчера, Бушера, Саттона, 21 марта 2019 г.