Диалог о двух главных мировых системах - Dialogue Concerning the Two Chief World Systems
Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Февраль 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В Диалог о двух главных мировых системах (Dialogo sopra i due massimi sistemi del mondo) - это 1632 г. Итальянский язык книга Галилео Галилей сравнивая Коперниканец система с традиционным Птолемеев система. На латынь это было переведено как Systema cosmicum[1] (Английский: Космическая система) в 1635 г. Маттиас Бернеггер.[2] Книга была посвящена покровителю Галилея, Фердинандо II Медичи, великий герцог Тосканы, получивший первый печатный экземпляр 22 февраля 1632 г.[3]
в Система Коперника, Земля и другие планеты вращаются вокруг Солнца, а в Система Птолемея, все во Вселенной вращается вокруг Земли. В Диалог был опубликован в Флоренция по официальной лицензии от Инквизиция. В 1633 году выяснилось, что Галилей «сильно подозревал ересь "на основе книги, которая затем была помещена на Указатель запрещенных книг, из которого он не был удален до 1835 года (после того, как теории, которые он обсуждал, были разрешены в печати в 1822 году).[4] В результате акции, о которой в то время не было объявлено, публикация всего, что он написал или когда-либо мог написать, также была запрещена в католических странах.[5]
Обзор
Во время написания книги Галилей называл ее своим Диалог о приливах, и когда рукопись была отправлена в инквизицию для утверждения, название было Диалог о приливах и отливах моря. Ему было приказано убрать все упоминания о приливах из названия и изменить предисловие, потому что одобрение такого названия выглядело бы как одобрение его теории. приливы используя движение Земли в качестве доказательства. В результате формальный заголовок на титульном листе выглядит так: Диалог, за которым следует имя Галилея, академические должности и длинный подзаголовок. Название, под которым теперь известно произведение, было извлечено типографом из описания на титульном листе, когда католическим богословом было дано разрешение на перепечатку с одобренным предисловием.[6] Об этом следует помнить при обсуждении мотивов написания книги Галилеем. Хотя книга представлена формально как рассмотрение обеих систем (а это необходимо для того, чтобы вообще ее опубликовать), нет никаких сомнений в том, что сторона Коперника берет верх над аргументом.[7]
Структура
Книга представляет собой серию дискуссий в течение четырех дней между двумя философами и неспециалистом:
- Сальвиати отстаивает позицию Коперника и прямо представляет некоторые взгляды Галилея, называя его «академиком» в честь членства Галилея в Accademia dei Lincei. Он назван в честь друга Галилея. Филиппо Сальвиати (1582–1614).
- Сагредо - умный обыватель, изначально настроенный нейтрально. Он назван в честь друга Галилея. Джованни Франческо Сагредо (1571–1620).
- Симпличио, преданный последователь Птолемей и Аристотель, представляет традиционные взгляды и аргументы против позиции Коперника. Предположительно он назван в честь Симплиций Киликийский, комментатор Аристотеля в шестом веке, но подозревали, что это имя было двусмысленным, поскольку итальянское слово «простой» (как в «простодушном») означает «простой».[8] Симпличио создан по образцу двух современных консервативных философов, Лодовико делле Коломбе (1565–1616?), Противник Галилея, и Чезаре Кремонини (1550–1631), коллега из Падуа, отказавшийся смотреть в телескоп.[9] Коломб был лидером группы флорентийских противников Галилея, которую некоторые друзья последнего называли «лигой голубей».[10]
Содержание
Обсуждение не ограничивается только астрономическими темами, но распространяется на большую часть современной науки. Некоторые из них призваны показать то, что Галилей считал хорошей наукой, например, обсуждение Уильям Гилберт Работаем по магнетизму. Другие части важны для дискуссии, поскольку они отвечают на ошибочные аргументы против движения Земли.
Классический аргумент против движения Земли - это отсутствие ощущения скорости у поверхности Земли, хотя она движется за счет вращения Земли со скоростью около 1700 км / ч на экваторе. В этой категории есть мысленный эксперимент в котором мужчина находится под палубой на корабль и не может сказать, пришвартован ли корабль или плавно движется по воде: он наблюдает, как вода капает из бутылки, рыба плавает в аквариуме, летают бабочки и т. д .; и их поведение одинаково независимо от того, движется корабль или нет. Это классическая экспозиция Инерциальная система отсчета и опровергает возражение о том, что если бы мы двигались на сотни километров в час во время вращения Земли, все, что упало бы, быстро отстало бы и унесло бы на запад.
Основная часть аргументов Галилея может быть разделена на три класса:
- Опровержения возражений традиционных философов; например, мысленный эксперимент на корабле.
- Наблюдения, несовместимые с моделью Птолемея: фазы Венеры например, что просто не могло произойти, или очевидные движения солнечные пятна, которое можно было объяснить только в системах Птолемея или Тихона как результат неправдоподобно сложной прецессии оси вращения Солнца.[11]
- Аргументы, показывающие, что элегантная объединенная теория Небес, которой придерживались философы и которая, как считалось, доказывала, что Земля неподвижна, была неверна; например, горы Луна, луны Юпитер, и само существование солнечных пятен, ни одно из которых не было частью старой астрономии.
В целом, эти аргументы хорошо подходят с точки зрения знаний следующих четырех столетий. Насколько убедительными они должны были быть для беспристрастного читателя в 1632 году, остается спорным вопросом.
Галилей попытался привести аргументы четвертого типа:
- Прямой физический аргумент в пользу движения Земли посредством объяснения приливов и отливов.
В качестве объяснения причин приливов или доказательства движения Земли это провал. Основной аргумент внутренне непоследователен и фактически приводит к выводу, что приливов не существует. Но Галилей любил споры и посвятил им «четвертый день» дискуссии. Степень его провала - как и почти все, что связано с Галилеем - вызывает споры. С одной стороны, все это недавно в печати описывалось как «хулиганство».[12] С другой стороны, Эйнштейн использовал совсем другое описание:
Именно тоска по механическому доказательству движения Земли заставила Галилея сформулировать неверную теорию приливов и отливов. В увлекательные аргументы в последнем разговоре Вряд ли Галилей принял бы это доказательство, если бы его темперамент не взял над ним верх. [Курсив добавлен][13][14]
Упущения

В Диалог не лечит Тихоническая система, которая стала предпочтительной системой многих астрономов на момент публикации и в конечном итоге оказалась неверной. Система Тихона - это неподвижная система Земли, но не система Птолемея; это гибридная система моделей Коперника и Птолемея. Меркурий и Венера вращаются вокруг Солнца (как в системе Коперника) маленькими кругами, в то время как Солнце, в свою очередь, вращается вокруг неподвижной Земли; Марс, Юпитер и Сатурн вращаются вокруг Солнца по гораздо большим кругам, что означает, что они также вращаются вокруг Земли. Система Тихона математически эквивалентна системе Коперника, за исключением того, что система Коперника предсказывает звездный параллакс, в то время как Тихонова система ничего не предсказывает. Звездный параллакс нельзя было измерить до 19 века, и поэтому в то время не было ни действительного опровержения системы Тихона на эмпирических основаниях, ни каких-либо решающих наблюдательных данных в пользу системы Коперника.
Галилей никогда не относился к системе Тихо всерьез, как видно из его переписки, считая ее неадекватным и физически неудовлетворительным компромиссом. Причину отсутствия системы Тихо (несмотря на многочисленные ссылки на Тихо и его работы в книге) можно искать в теории приливов Галилея, которая дала первоначальное название и организационный принцип Диалог. Ибо, хотя системы Коперника и Тихоника эквивалентны геометрически, они совершенно разные динамически. Теория приливов Галилея влекла за собой реальное физическое движение Земли; то есть, если бы это было так, это было бы доказательством того, что Маятник Фуко очевидно, предоставлен двумя веками позже. Что касается приливной теории Галилея, не будет никакой разницы между системами Птолемея и Тихона.
Галилей также не обсуждает возможность некруглых орбит, хотя Иоганн Кеплер прислал ему копию своей книги 1609 года, Astronomia nova, в котором он предлагает эллиптические орбиты, правильно рассчитывая орбиту Марса.[15] Принц Федерико Чези в письме Галилею 1612 г. законы движения планет представлены в книге как общеизвестные;[16][17] Третий закон Кеплера был опубликован в 1619 году. Через четыре с половиной десятилетия после смерти Галилея Исаак Ньютон опубликовал свой законы движения и сила тяжести, из которого можно вывести гелиоцентрическую систему с планетами на приблизительно эллиптических орбитах.
Резюме
Предисловие: Для взыскательного читателяссылается на запрет «пифагорейского мнения о движении Земли» и говорит, что автор «принимает сторону Коперника с чистой математической гипотезой». Он представляет друзей Сагредо и Сальвиати с которыми он беседовал, а также странствующий философ Simplicio.
День первый
Он начинает с доказательства Аристотелем полноты и совершенства мира (то есть вселенной) в силу ее трех измерений. Симпличио указывает, что пифагорейцы предпочитали три ноги, тогда как Сальвиати не может понять, почему три ноги лучше двух или четырех. Он предполагает, что числа были «мелочами, которые позже распространились среди простонародья», и что их определения, такие как прямые и прямые углы, были более полезны при установлении размеров. Симпличио ответил, что Аристотель считал, что в физических вопросах математические доказательства не всегда нужны.
Сальвиати нападает на аристотелевское определение неба как нетленного и неизменного, в то время как только зона, ограниченная Луной, показывает изменение. Он указывает на изменения, наблюдаемые в небе: новые звезды 1572 и 1604 и солнечные пятна, сквозь новый телескоп. Существует дискуссия об использовании Аристотелем априори аргументы. Сальвиати предполагает, что он использует свой опыт, чтобы выбрать подходящий аргумент, чтобы доказать, как это делают другие, и что он изменит свое мнение в нынешних обстоятельствах.
Симпличио утверждает, что солнечные пятна могут быть просто небольшими непрозрачными объектами, проходящими перед Солнцем, но Сальвиати указывает, что некоторые из них появляются или исчезают случайным образом, а те, что на краю, сплющены, в отличие от отдельных тел. Следовательно, «лучше аристотелевской философии сказать:« Небеса изменчивы, потому что мои чувства говорят мне », чем« Небеса неизменны, потому что Аристотеля так убедили рассуждения ».
Эксперименты с зеркалом используются, чтобы показать, что поверхность Луны должна быть непрозрачной, а не идеальной кристаллической сферой, как считает Симпличио. Он отказывается признать, что горы на Луне вызывают тени или что отраженный свет от Земли ответственен за слабые очертания полумесяца.
Сагредо считает, что он считает Землю благородной из-за изменений в ней, тогда как Симпличио говорит, что изменения Луны или звезд были бы бесполезны, потому что они не приносят пользу человеку. Сальвиати отмечает, что дни на Луне длятся месяц, и, несмотря на разнообразную местность, которую показал телескоп, она не может поддерживать жизнь. Люди познают математические истины медленно и неуверенно, тогда как Бог знает их всю бесконечность интуитивно. И если посмотреть на чудесные вещи, которые люди поняли и придумали, то ясно, что человеческий разум - одно из самых превосходных творений Бога.
День второй
Второй день начинается с повторения, что Аристотель изменил бы свое мнение, если бы увидел то, что видели они. «Его авторитетом короновали последователи Аристотеля, а не он, узурпировал или присвоил его себе».
Есть одно высшее движение - то, при котором Солнце, Луна, планеты и неподвижные звезды, кажется, перемещаются с востока на запад за 24 часа. Это может логически принадлежать только Земле, как и всей остальной Вселенной. Аристотель и Птолемей, которые это понимали, не возражают против какого-либо другого движения, кроме суточного.
Движение относительное: положение мешков с зерном на корабле может быть идентичным в конце рейса, несмотря на движение корабля. Почему мы должны верить, что природа перемещает все эти чрезвычайно большие тела с невероятными скоростями, а не просто перемещает землю среднего размера? Если убрать Землю с картинки, что произойдет со всем движением?
Движение небес с востока на запад противоположно всем другим движениям небесных тел, которые происходят с запада на восток; вращение Земли приводит ее в соответствие со всеми остальными. Хотя Аристотель утверждает, что круговые движения не противоречат друг другу, они все же могут приводить к столкновениям.
Для больших орбит планет требуется больше времени, чем для более коротких: для Сатурна и Юпитера требуется много лет, для Марса - два, а для Луны - всего месяц. Спутники Юпитера забирают еще меньше. Это не изменится, если Земля вращается каждый день, но если Земля неподвижна, мы внезапно обнаружим, что сфера неподвижных звезд вращается за 24 часа. Учитывая расстояния, разумнее было бы, чтобы это были тысячи лет.
Вдобавок некоторые из этих звезд должны двигаться быстрее, чем другие: если бы Полярная звезда была точно на оси, то она была бы полностью неподвижной, тогда как звезды на экваторе имели невообразимую скорость. Прочность этой предполагаемой сферы непостижима. Сделайте землю Primum Mobile и потребность в этой дополнительной сфере отпадает.

Они рассматривают три основных возражения против движения Земли: что падающее тело будет оставлено Землей позади и, таким образом, упадет далеко к западу от своей точки высвобождения; что пушечное ядро, выпущенное на запад, точно так же полетит намного дальше, чем ядро, выпущенное на восток; и что пушечное ядро, выпущенное вертикально, также упадет далеко на запад. Сальвиати показывает, что они не принимают во внимание толчок пушки.
Он также указывает, что попытка доказать, что Земля не движется с помощью вертикального падения, приводит к логической ошибке паралогизм (предполагая то, что должно быть доказано), потому что если Земля движется, то только на вид она падает вертикально; на самом деле оно падает под наклоном, как это бывает с пушечным ядром, проходящим сквозь пушку (показано).
Опровергая работу, в которой утверждается, что мяч, падающий с Луны, должен прибыть через шесть дней, вводится правило нечетных чисел: тело, падающее на 1 единицу в интервале, упадет на 3 единицы в следующем интервале и 5 единиц в последующем. единица и т. д. Отсюда возникает правило, согласно которому пройденное расстояние соответствует квадрату времени. Используя это, он подсчитал, что на самом деле время немногим больше 3 часов. Он также указывает, что плотность материала не имеет большого значения: свинцовый шар может ускоряться только в два раза быстрее, чем пробковый.
Фактически, мяч, падающий с такой высоты, будет не отставать от вертикали, а опережать ее, поскольку вращательное движение будет происходить по постоянно уменьшающимся кругам. То, что заставляет Землю двигаться, похоже на то, что движет Марс или Юпитер, и то же самое, что притягивает камень к Земле. Называя это сила тяжести не объясняет, что это такое.
День третий
Сальвиати начинает с отклонения аргументов книги против novas он читал всю ночь.[18] В отличие от комет, они были стационарными, и их отсутствие параллакса легко контролировалось, и поэтому они не могли находиться в подлунной сфере.
Теперь Симплисио приводит величайший аргумент против ежегодного движения Земли: если она движется, то больше не может быть центром зодиака, мира. Аристотель доказывает, что Вселенная конечна, ограничена и сферична. Сальвиати указывает, что они исчезают, если он отрицает предположение, что оно подвижно, но допускает исходное предположение, чтобы не множить споры.
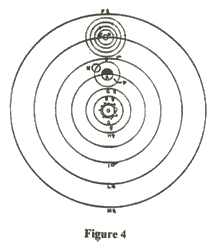
Он указывает, что если что-то и является центром, то это должно быть Солнце, а не Земля, потому что все планеты находятся ближе или дальше от Земли в разное время, а Венера и Марс - до восьми раз. Он призывает Симпличио составить план планет, начиная с Венеры и Меркурия, которые, как легко заметить, вращаются вокруг Солнца. Марс также должен вращаться вокруг Солнца (а также Земли), поскольку его никогда не видят. рогатый в отличие от Венеры, которую теперь можно увидеть в телескоп; то же самое с Юпитером и Сатурном. Земля, которая находится между Марсом с периодом в два года и Венерой с периодом в девять месяцев, имеет период в год, который более элегантно можно отнести к движению, чем к состоянию покоя.
Сагредо выдвигает два других распространенных возражения. Если Земля вращается, горы скоро окажутся в таком положении, что по ним придется спускаться, а не подниматься. Во-вторых, движение будет настолько быстрым, что кто-то на дне колодца сможет лишь на короткое время увидеть звезду, когда она движется. Симпличио может видеть, что первое ничем не отличается от путешествия по земному шару, как и любой, кто совершил кругосветное путешествие, но хотя он понимает, что второе такое же, как если бы небо вращалось, он все еще не понимает этого. Сальвиати говорит, что первый ничем не отличается от тех, кто отрицает антиподы. Во втором он побуждает Симпличио решить, какую часть неба можно увидеть из колодца.
Сальвиати поднимает другую проблему, заключающуюся в том, что Марс и Венера не так изменчивы, как предполагает теория. Он объясняет, что размер звезды для человеческого глаза зависит от яркости, а размеры не соответствуют действительности. Это решается с помощью телескопа, который также показывает форму полумесяца Венеры. Еще одно возражение против движения Земли, уникального существования Луны, было разрешено открытием спутники Юпитера, которая для любого юпитериана может показаться земной Луной.
Копернику удалось уменьшить некоторые неравномерные движения Птолемея, которому приходилось иметь дело с движениями, которые иногда идут быстро, иногда медленно, а иногда и в обратном направлении, с помощью обширных эпициклы. Марс, находящийся над сферой Солнца, часто опускается намного ниже ее, а затем парит над ней. Эти аномалии излечиваются годовым движением Земли. Это объясняется диаграммой, на которой изменяющееся движение Юпитера показано с использованием орбиты Земли.
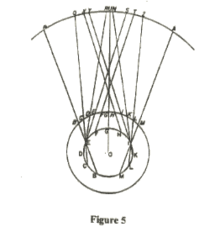
Симпличио выпускает еще один буклет, в котором богословские аргументы смешаны с астрономическими, но Сальвиати отказывается затрагивать вопросы из Священного Писания. Поэтому он приводит аргумент, что неподвижные звезды должны находиться на невероятном расстоянии, причем самые маленькие из них должны быть больше, чем вся орбита Земли. Сальвиати объясняет, что все это происходит из-за неправильного толкования слов Коперника, что привело к огромному перерасчету размера звезды шестой величины. Но многие другие известные астрономы переоценили размер звезд, игнорируя фактор яркости. Даже Тихо с его точными приборами не смог измерить размер любой звезды, кроме Солнца и Луны. Но Сальвиати (Галилей) смог сделать разумную оценку, просто повесив шнур, чтобы скрыть звезду, и измерив расстояние от глаза до шнура.
Но все же многие не могут поверить, что неподвижные звезды по отдельности могут быть такими же большими или крупными, как Солнце. Для чего это? Сальвиати утверждает, что «из-за нашей слабости глупо пытаться судить о причинах действий Бога и называть все во вселенной тщетным и лишним, что не служит нам».
Пытался ли Тихо или кто-либо из его учеников каким-либо образом исследовать явления, которые могли бы подтвердить или опровергнуть движение Земли? Кто-нибудь из них знает, сколько вариация нужно в неподвижных звездах? Симплисио возражает против того, чтобы признать, что расстояние до неподвижных звезд слишком велико, чтобы его можно было обнаружить. Сальвиати отмечает, насколько сложно даже обнаружить различные расстояния до Сатурна. Многие положения неподвижных звезд не известны точно, и нужны гораздо лучшие инструменты, чем у Тихо: скажем, использование прицела с фиксированным положением на расстоянии 60 миль.
Затем Сагредо просит Сальвиати объяснить, как система Коперника объясняет времена года и неравенство ночи и дня. Он делает это с помощью диаграммы, показывающей положение Земли по четырем временам года. Он указывает, насколько она проще, чем система Птолемея. Но Симпличио считает, что Аристотель поступил мудро, избежав излишней геометрии. Он предпочитает аксиому Аристотеля избегать более чем одного простого движения за раз.
День четвертый
Они находятся в доме Сагредо в Венеция, где приливы являются важной проблемой, а Сальвиати хочет показать влияние движения Земли на приливы. Сначала он указывает на три периода приливов: ежедневно (суточный)обычно с интервалами 6 часов подъема и еще 6 часов спада; ежемесячно, по-видимому, с Луны, которая увеличивает или уменьшает эти приливы; и ежегодный, что приводит к разным размерам в равноденствиях.
Сначала он рассматривает ежедневное движение. Наблюдаются три разновидности: в некоторых местах вода поднимается и опускается без движения вперед; в других они движутся на восток и обратно на запад, не поднимаясь и не падая; в третьих есть сочетание того и другого - это происходит в Венеции, где вода поднимается при входе и опускается при выходе. в Мессинский пролив есть очень быстрые токи между Сцилла и Харибда. В открытую Средиземноморье изменение высоты небольшое, но токи заметны.
Simplicio счетчики с странствующий объяснения, которые основаны на морских глубинах и господстве Луны над водой, хотя это не объясняет восходы, когда Луна находится ниже горизонта. Но он признает, что это могло быть чудом.
Когда вода в Венеции поднимается, откуда она берется? На Корфу или Дубровнике подъемов мало. Из океана через Гибралтарский пролив ? Это слишком далеко, и токи слишком медленные.
Так могло ли движение контейнера вызвать нарушение? Рассмотрим баржи, доставляющие воду в Венецию. Когда они сталкиваются с препятствием, вода устремляется вперед; когда они ускорятся, он пойдет назад. При всех этих нарушениях нет необходимости в новой воде, а уровень в середине остается в основном постоянным, хотя вода там устремляется вперед и назад.
Рассмотрим точку на Земле, находящуюся под совместным действием годового и суточного движений. В один момент они складываются вместе, а через 12 часов они действуют друг против друга, поэтому есть чередование ускорения и замедления. Таким образом, океанские бассейны страдают так же, как и баржа, особенно в направлении восток-запад. Длина баржи влияет на скорость колебаний, так же как длина отвеса изменяет ее скорость. Глубина воды также влияет на величину вибраций.
Первичный эффект объясняет приливы только один раз в день; нужно искать в другом месте шестичасовое изменение, период колебаний воды. В некоторых местах, например Геллеспонт и Эгейское море периоды более короткие и изменчивые. Но море с севера на юг, подобное красное море имеет очень небольшой прилив, в то время как Мессинский пролив несет сдерживающее влияние двух бассейнов.
Симплисио возражает, что, если это объясняет воду, разве не следует ли ее еще больше видеть на ветру? Сальвиати предполагает, что вмещающие бассейны не так эффективны, и воздух не поддерживает его движение. Тем не менее, эти силы видны устойчивый ветер с востока на запад в океанах в жаркая зона.
Кажется, что Луна также участвует в создании ежедневных эффектов, но это ему противно. Движение Луны доставило астрономам большие трудности. Полностью учесть все это невозможно, учитывая нерегулярность морских бассейнов.
Смотрите также
- "Беседа о приливах ", 1616 г. Очерк Галилея
Примечания
- ^ Морис А. Финоккиаро: Повторная попытка Галилея, 1633–1992, Калифорнийский университет Press, 2007 г. ISBN 0-520-25387-6, ISBN 978-0-520-25387-2
- ^ Журнал истории астрономии, 2005 г.
- ^ Гиндикин, Семен Григорьевич (1988). Сказки физиков и математиков. Биркхойзер. п. 62. ISBN 978-0-8176-3317-2. Получено 22 февраля 2011.
- ^ Суд над Галилеем: хронология В архиве 2007-02-05 на Wayback Machine
- ^ Видеть Дело Галилея для получения более подробной информации, включая источники.
- ^ Дрейк, Стиллман (1990). Галилей: Ученый-пионер. U of Toronto Press. п.187. ISBN 0-8020-2725-3.
- ^ Кестлер, Артур (1989). Лунатики. Пингвин Аркана. п.480.
- ^ Артур Кестлер, Лунатики: история меняющегося видения Вселенной человеком (1959), Penguin Books, издание 1986 года: ISBN 0-14-055212-X, 978014055212X 1990 г. перепечатка: ISBN 0-14-019246-8, ISBN 978-0-14-019246-9 [1]
- ^ Стиллман Дрейк: Галилей за работой: его научная биография, Courier Dover Publications, 2003 г., ISBN 0-486-49542-6, стр. 355: Кремонини и делле Коломб
- ^ "La legha del pippione". «Пиппионе» - это игра слов от фамилии Коломба, которая является множественным числом итальянского слова «голубь». Друзья Галилея, художника, Лодовико Карди да Чиголи (на итальянском), его бывшая ученица, Бенедетто Кастелли, и пара других его корреспондентов часто называла Коломба «il Colombo», что означает «Голубь». Сам Галилей использовал этот термин несколько раз в письме к Чиголи в октябре 1611 года. (Национальное издание, 11: 214). Более насмешливое прозвище "il Pippione", иногда используемое Cigoli (Национальное издание 11: 176, 11:229, 11:476,11:502), это теперь архаичное итальянское слово с тройным смыслом. Помимо значения «молодой голубь», это еще и шутливый термин, обозначающий яичко, и на тосканском диалекте слово «дурак».
- ^ Дрейк, (1970, стр.191–196), Линтон (2004, стр. 211–12), Шарратт (1994, п. 166). Однако это неверно для геоцентрических систем, таких как предложенная Лонгомонтан - в котором вращалась Земля. В таких системах видимое движение солнечных пятен можно объяснить так же легко, как и в случае Коперника.
- ^ Тимоти Мой (сентябрь 2001 г.). "Наука, религия и дело Галилея". Скептический вопрошатель. 25 (5): 43–49. Архивировано из оригинал 29 января 2009 г.
- ^ "Предисловие; Альберт Эйнштейн; Авторизованный перевод Сони Баргманн". Архивировано из оригинал на 2007-09-25.(отрывки опущены)
- ^ Пол Мэйнвуд (9 августа 2003 г.). «Мысленные эксперименты в математической философии Галилея и Ньютона» (PDF). 7-я ежегодная конференция выпускников Оксфордской философии. 7-я ежегодная конференция выпускников Оксфордской философии. Архивировано из оригинал (PDF) 22 сентября 2006 г., цитируя страницу xvii предисловия Эйнштейна в Г. Галилей (1953) [1632]. Диалог о двух главных мировых системах. Перевод Стилмана Дрейка. Беркли и Лос-Анджелес, Калифорния: Калифорнийский университет Press.
- ^ Гиллиспи, Чарльз Коулстон (1960). Грань объективности: очерк истории научных идей. Издательство Принстонского университета. п. 51. ISBN 0-691-02350-6.
- ^ Опера Галилея, изд. Наз., XI (Флоренция, 1901 г.), страницы 365-367
- ^ «Кеплер», Макс Каспар, стр. 137
- ^ Кьярамонти, Сципион (1628 г.). De tribus novis stellis.
Библиография
- Дрейк, Стиллман (1970). Исследования Галилея. Анн-Арбор: Издательство Мичиганского университета. ISBN 0-472-08283-3.
- Линтон, Кристофер М. (2004). От Евдокса до Эйнштейна - история математической астрономии. Кембридж: Издательство Кембриджского университета. ISBN 978-0-521-82750-8.
- Шаррат, Майкл (1994). Галилей: решительный новатор. Кембридж: Издательство Кембриджского университета. ISBN 0-521-56671-1.
внешняя ссылка
- Итальянский текст с цифрами (на итальянском)
- Английский перевод Томаса Салусбери 1661 г. Диалог. Он-лайн копия полного текста.
- Длинный, но сжатый отрывок из перевода Стилмана Дрейка 1953 г. Диалог. Несмотря на заголовок вверху страницы, полный текст, на который все еще распространяется авторское право, не приводится. Например, опускается весь «четвертый день».
- Еще один длинный отрывок из перевода Дрейка 1953 года. Это также не включает полный текст.
- Dialogo dei massimi sistemi. Фьоренца, Пер Джио: Батиста Ландини, 1632 год. Отдел редких книг и особых коллекций на Библиотека Конгресса

