Расширенный метод дискретных элементов - Википедия - Extended discrete element method

В расширенный метод дискретных элементов (XDEM) - это численный метод, который расширяет динамику зернистого материала или частиц, как описано в классическом метод дискретных элементов (DEM) (Cundall[1] и Аллен[2]) дополнительными свойствами, такими как термодинамический государственный, стресс /напряжение или же электромагнитный поле для каждой частицы. В отличие от механика сплошной среды Концепция XDEM направлена на разделение фазы твердых частиц с ее различными процессами, связанными с частицами. В то время как метод дискретных элементов предсказывает положение и ориентацию в пространстве и времени для каждой частицы, расширенный метод дискретных элементов дополнительно оценивает такие свойства, как внутренние температура и / или разновидность распространение или механическое воздействие на конструкции.
История
Молекулярная динамика, разработанная в конце 1950-х годов Alder et al.[3] и начало 1960-х годов Рахманом[4] можно рассматривать как первый шаг к расширенному методу дискретных элементов, хотя силы, возникающие из-за столкновений между частицами, были заменены энергетическими потенциалами, например Леннард-Джонс потенциалы молекулы и атомы как дальнобойные силы для определения взаимодействия.
Аналогично исследовалось гидродинамическое взаимодействие взвешенных в потоке частиц. В тащить Силы, действующие на частицы со стороны их относительной скорости и потока, рассматривались как дополнительные силы, действующие на частицы. Следовательно, эти многофазный поток явления, включающие твердую, например, твердую и газообразную или жидкую фазу, разрешают дисперсную фазу дискретными методами, в то время как поток газа или жидкости описывается непрерывными методами и, следовательно, обозначается как комбинированная непрерывная и дискретная модель (CCDM), применяемая Кавагути. и другие.,[5] Хуманс,[6] Сюй 1997[7] и Сюй 1998.[8] Из-за дискретного описания твердой фазы учредительный отношения опущены, и, следовательно, приводит к лучшему пониманию основ. К этому же выводу пришли Zhu 2007 et al.[9] и Zhu 2008 et al.[10] во время обзора потоков твердых частиц, смоделированных с использованием подхода CCDM. За последние два десятилетия он получил развитие и описывает движение твердой фазы Метод дискретных элементов (DEM) в масштабе отдельных частиц, а остальные фазы обрабатываются Навье-Стокса уравнения. Таким образом, этот метод признан эффективным инструментом для исследования взаимодействия между твердыми частицами и жидкой фазой, как это сделали Ю и Сюй,[11] Фэн и Ю [12] и Deen et al.[13] На основе методологии CCDM характеристики фонтанирующих и псевдоожиженных слоев прогнозируются Gryczka et al.[14]
Теоретическая основа XDEM была разработана в 1999 г. Петерсом,[15] который описал сжигание деревянной движущейся кровати на решетке прямого действия.[16] Позднее эта концепция была использована Sismsek et al.[17] для прогноза топочного процесса колосниковой системы. Шунго и др. Попытались применить его к сложным процессам в доменной печи.[18] Численное моделирование закачки флюида в газовую среду в настоящее время используется большим количеством кодов CFD, таких как Simcenter STAR-CCM +, ANSYS и AVL -Огонь. Капли спрея обрабатываются с помощью нульмерного подхода для учета тепломассопереноса в жидкую фазу.
Методология

Существует множество инженерных проблем, которые включают непрерывные и дискретные фазы, и эти проблемы невозможно точно смоделировать с помощью непрерывных или дискретных подходов. XDEM предоставляет решение для некоторых из этих инженерных приложений.
Хотя исследования и разработки численных методов в каждой области дискретных и непрерывных решателей все еще продолжаются, программные инструменты доступны. Для объединения дискретного и непрерывного подходов доступны два основных подхода:
- Монолитный подход: Уравнения, описывающие мультифизические явления, решаются одновременно одним решателем, что дает полное решение.
- Разделенный или поэтапный подход: Уравнения, описывающие мультифизические явления, решаются последовательно специально подобранными и отдельными решателями с передачей результатов одного анализа в качестве нагрузки другому.
Первый подход требует решателя, который решает все физические проблемы, поэтому требует больших усилий по реализации. Однако существуют сценарии, для которых сложно подобрать коэффициенты комбинированного дифференциальные уравнения в одной матрица.
Последний, разделенный подход, объединяет несколько решателей, представляющих отдельные области физики, дает преимущества по сравнению с монолитной концепцией. Он обладает большей гибкостью, поскольку может использовать множество решателей. Кроме того, это позволяет разрабатывать более модульное программное обеспечение. Однако моделирование с разбиением на части требует стабильных и точных алгоритмов связи.
В рамках разнесенной концепции XDEM непрерывные поля описываются решением соответствующих непрерывных уравнений (сохранения). Свойства отдельных частиц, такие как температура, также решаются путем решения соответствующих уравнений сохранения, которые дают как пространственное, так и временное внутреннее распределение соответствующих переменных. Основные принципы сохранения с их уравнениями и переменными, которые необходимо решить и которые применяются к отдельной частице в XDEM, перечислены в следующей таблице.
| Закон сохранения | Уравнение | Переменная |
|---|---|---|
| Масса (сжимаемая среда) | Непрерывность | Давление / плотность |
| Линейный импульс | Навье-Стокса | Скорость |
| Энергия | Энергия | Температура |
| Масса вида | Транспорт видов | Массовые доли |
| Заряд, ток | Максвелл | электрическое, магнитное поле, электрическое поле смещения |
Решение этих уравнений в принципе определяет трехмерное и переходное поле соответствующих переменных, таких как температура или виды. Однако применение этих принципов сохранения к большому количеству частиц обычно ограничивает разрешение не более чем одним репрезентативным измерением и временем из-за потребления времени процессора. Экспериментальные данные, по крайней мере, в реакционной инженерии, подтверждают предположение об одномерности, как указали Мэн и Бён:[19] в то время как важность переходного поведения подчеркивается Lee et al.[20]
Приложения

Проблемы, связанные как с непрерывной, так и с дискретной фазой, важны для таких разнообразных приложений, как фармацевтическая промышленность, например, производство лекарств, сельское хозяйство, пищевая и перерабатывающая промышленность, горнодобывающая промышленность, строительство и сельскохозяйственное машиностроение, производство металлов, производство энергии и системная биология. Некоторыми преобладающими примерами являются кофе, кукурузные хлопья, орехи, уголь, песок, возобновляемые виды топлива, например, биомасса для производства энергии и удобрения.
Первоначально такие исследования ограничивались простыми конфигурациями потоков, как указал Хуманс,[21] однако Чу и Ю[22] продемонстрировали, что метод может быть применен к сложной конфигурации потока, состоящей из псевдоожиженного слоя, конвейерной ленты и циклона. Аналогичным образом Zhou et al.[23] применили подход CCDM к сложной геометрии горелки для обогащенного / обедненного топлива для сжигания пылевидного угля на заводе, а Chu et al.[24] смоделировал сложное течение воздуха, воды, частиц угля и магнетита разного размера в плотной среде. циклон (DMC).
Подход CCDM также применялся к псевдоожиженным слоям, как это было рассмотрено Роу и Ниенов.[25] и Фэн и Ю[26] и применен Фэном и Ю[27] к хаотическому движению частиц разных размеров в псевдоожиженном слое газа. Кафуйя и др.[28] описывают моделирование псевдоожиженных слоев на основе дискретных частиц и континуума. Дальнейшее применение XDEM включает термическое преобразование биомассы на решетке прямого и обратного действия. Теплопередача в системах с термическими / реагирующими твердыми частицами также была решена и исследована, что подробно описано Peng et al.[29] В деформация конвейерной ленты из-за удара гранулированный материал который выгружается через желоб, представляет собой применение в области стресс /напряжение анализ.
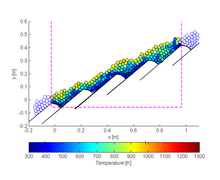 Распределение температуры поверхности частиц на решетке обратного действия. |  Ход пиролиза соломенных ножей на решетке прямого действия, на которой солома превращается в обугленный материал |  Распределение пористости внутри уплотненного слоя и температуры частиц |
Рекомендации
- ^ Cundall, P.A .; Страк, О. Д. Л. (1979). «Дискретная численная модель для зернистых сборок». Геотехника. 29: 47–65. Дои:10.1680 / geot.1979.29.1.47.
- ^ Аллен, М. П.; Тилдесли, Д. Дж. (1990). Компьютерное моделирование жидкостей. Кларедон Пресс Оксфорд.
- ^ Alder, B.J .; Уэйнрайт, Т. Э. (1959). «Исследования молекулярной динамики. I. Общий метод». J. Chem. Phys. 31 (2): 459–466. Bibcode:1959ЖЧФ..31..459А. Дои:10.1063/1.1730376.
- ^ Рахман, А. (1964). «Корреляции в движении атомов в жидком аргоне». Phys. Rev. 136 (2A): A405 – A411. Bibcode:1964ПхРв..136..405Р. Дои:10.1103 / Physrev.136.a405.
- ^ Кавагути, Т .; Tsuji, Y .; Танака, Т. (1993). «Дискретное моделирование двумерного псевдоожиженного слоя с использованием частиц». Пудра Технол. 77: 79–87. Дои:10.1016/0032-5910(93)85010-7.
- ^ Хуманс, Б. П. Б .; Kuipers, J. A. M .; Briels, W. J .; Ван Свайдж, В. П. М. (1996). «Дискретное моделирование образования пузырьков и пробок в двумерном газо-псевдоожиженном слое: подход твердых сфер». Chem. Англ. Наука. 51: 99–118. CiteSeerX 10.1.1.470.6532. Дои:10.1016/0009-2509(95)00271-5.
- ^ Xu, B.H .; Ю., А. Б. (1997). «Численное моделирование течения газ-твердое тело в псевдоожиженном слое путем комбинирования метода дискретных частиц с вычислительной гидродинамикой». Химическая инженерия. 52 (16): 2785–2809. Дои:10.1016 / с0009-2509 (97) 00081-х.
- ^ Xu, B.H .; Ю., А. Б. (1998). «Комментарии к статье о численном моделировании течения газ-твердое тело в псевдоожиженном слое путем комбинирования метода дискретных частиц с вычислительной гидродинамикой». Химическая инженерия. 53 (14): 2646–2647. Дои:10.1016 / с0009-2509 (98) 00086-4.
- ^ Zhu, H.P .; Zhou, Z. Y .; Yang, R. Y .; Ю., А. Б. (2007). "Дискретное моделирование частиц систем твердых частиц: теоретические разработки". Химическая инженерия. 62 (13): 3378–3396. Дои:10.1016 / j.ces.2006.12.089.
- ^ Zhu, H.P .; Zhou, Z. Y .; Yang, R. Y .; Ю., А. Б. (2008). «Дискретное моделирование частиц систем твердых частиц: обзор основных приложений и результатов». Химическая инженерия. 63 (23): 5728–5770. Дои:10.1016 / j.ces.2008.08.006.
- ^ Xu, B.H .; Ю., А. Б. (2003). «Масштабное моделирование газо-твердого потока при псевдоожижении». Журнал химической технологии и биотехнологии. 78 (2–3): 111–121. Дои:10.1002 / jctb.788.
- ^ Feng, Y. Q .; Ю., А. Б .; Ю., А. Б .; Винс, А. (2004). «Оценка модельных постановок при дискретном моделировании газо-твердотельного потока». Промышленные и инженерные химические исследования. 43 (26): 8378–8390. Дои:10.1021 / ie049387v.
- ^ Deen, N.G .; Annaland, M.V.S .; Van Der Hoef, M.A .; Койперс, Дж. А. М. (2007). «Обзор моделирования псевдоожиженного слоя дискретными частицами». Химическая инженерия. 62 (1–2): 28–44. Дои:10.1016 / j.ces.2006.08.014.
- ^ Gryczka, O .; Генрих, С .; Deen, N. S .; van Sint Annaland, M .; Kuipers, J. A. M .; Мёрл, М. (2009). «CFD моделирование призматического фонтанирующего слоя с двумя регулируемыми входами газа». Канадский журнал химической инженерии. 87 (2): 318–328. CiteSeerX 10.1.1.335.4108. Дои:10.1002 / cjce.20143.
- ^ Петерс, Б. (1999). «Классификация режимов горения в насадочном слое на основе соответствующих шкал времени и длины». Горение и пламя. 116 (1–2): 297–301. Дои:10.1016 / с0010-2180 (98) 00048-0.
- ^ Петерс, Б. (2002). «Измерения и применение модели дискретных частиц (DPM) для моделирования горения уплотненного слоя отдельных частиц топлива». Горение и пламя. 131 (1–2): 132–146. Дои:10.1016 / с0010-2180 (02) 00393-0.
- ^ Simsek, E .; Brosch, B .; Wirtz, S .; Scherer, V .; Крёлль, Ф. (2009). "Численное моделирование топочных систем колосниковой решетки с использованием комбинированного метода CFD / дискретных элементов (DEM)". Порошковая технология. 193 (3): 266–273. Дои:10.1016 / j.powtec.2009.03.011.
- ^ Нацуи, Шунго; Уэда, Сигеру; Фань, Чжэнъюнь; Андерссон, Нильс; Кано, Джунья; Иноуэ, Ре; Арияма, Тацуро (2010). «Характеристики течения твердых тел и распределение напряжений, включая асимметричные явления в доменной печи, проанализированы методом дискретных элементов». ISIJ International. 50 (2): 207–214. Дои:10.2355 / isijinternational.50.207.
- ^ Man, Y.H .; Бён, Р. К. (1994). «Численное исследование горения одиночной частицы углерода, увлеченной стационарным потоком». Горение и пламя. 97: 1–16. Дои:10.1016/0010-2180(94)90112-0.
- ^ Lee, J.C .; Йеттер, Р. А .; Сушилка, Ф. Л. (1996). «Численное моделирование лазерного зажигания изолированной частицы углерода в спокойной среде». Горение и пламя. 105 (4): 591–599. Дои:10.1016/0010-2180(96)00221-0.
- ^ Хуманс, Б. П. Б .; Kuipers, J. A. M .; Briels, W. J .; Ван Свайдж, В. П. М. (1996). «Дискретное моделирование образования пузырьков и пробок в двумерном газо-псевдоожиженном слое: подход твердых сфер». Chem. Англ. Наука. 51: 99–118. CiteSeerX 10.1.1.470.6532. Дои:10.1016/0009-2509(95)00271-5.
- ^ Чу, К. З .; Ю., А. Б. (2008). «Численное моделирование сложных течений частица-жидкость». Порошковая технология. 179 (3): 104–114. Дои:10.1016 / j.powtec.2007.06.017.
- ^ Чжоу, H .; Mo, G .; Zhao, J .; Цен, К. (2011). «DEM-CFD моделирование дисперсии частиц в двухфазном потоке газ-твердое тело для горелки с высоким / обедненным топливом». Топливо. 90 (4): 1584–1590. Дои:10.1016 / j.fuel.2010.10.017.
- ^ Чу, К. З .; Ван, Б .; Ю., А. Б .; Винс, А .; Barnett, G.D .; Барнетт, П. Дж. (2009). «Исследование CFD-DEM влияния распределения плотности частиц на многофазный поток и производительность циклона с плотной средой». Минерал Инжиниринг. 22 (11): 893–909. Дои:10.1016 / j.mineng.2009.04.008.
- ^ Rowe, P.N .; Ниенов, А. В. (1976). «Смешивание и сегрегация частиц в псевдоожиженных слоях газа: обзор». Порошковая технология. 15 (2): 141–147. Дои:10.1016/0032-5910(76)80042-3.
- ^ Feng, Y. Q .; Ю., А. Б .; Ю., А. Б .; Винс, А. (2004). «Оценка модельных постановок при дискретном моделировании течения твердых частиц и газа». Промышленные и инженерные химические исследования. 43 (26): 8378–8390. Дои:10.1021 / ie049387v.
- ^ Feng, Y. Q .; Ю., А. Б. (2008). «Анализ хаотического движения частиц разного размера в газовом псевдоожиженном слое». Партикуология. 6 (6): 549–556. Дои:10.1016 / j.partic.2008.07.011.
- ^ Kafuia, K. D .; Thornton, C .; Адамс, М. Дж. (2002). «Дискретное моделирование сплошной среды в псевдоожиженном слое газ-твердое тело». Химическая инженерия. 57 (13): 2395–2410. Дои:10.1016 / с0009-2509 (02) 00140-9.
- ^ Peng, Z .; Doroodchi, E .; Могтадери, Б. (2020). «Моделирование теплопередачи в моделировании тепловых процессов на основе метода дискретных элементов (DEM): теория и разработка моделей». Прогресс в области энергетики и горения. 79,100847: 100847. Дои:10.1016 / j.pecs.2020.100847.
