Гидродинамика сглаженных частиц - Smoothed-particle hydrodynamics

Схематическое изображение свертки SPH

Гидродинамика сглаженных частиц (SPH) - это вычислительный метод, используемый для моделирования механики сплошных сред, таких как механика твердого тела и жидкость потоки. Он был разработан Gingold и Монаган ^[1] и Люси^[2] в 1977 г., первоначально для астрофизических задач. Он использовался во многих областях исследований, в том числе астрофизика, баллистика, вулканология, и океанография. Это без сетки Лагранжев метод (где координаты движутся вместе с жидкостью), а разрешение метода можно легко отрегулировать относительно таких переменных, как плотность.

Метод

Преимущества

• По построению SPH является метод без сетки, что делает его идеально подходящим для моделирования задач, в которых преобладает сложная граничная динамика, например, потоки со свободной поверхностью или большие граничные смещения.
• Отсутствие сетки значительно упрощает реализацию модели и ее распараллеливание даже для многоядерный архитектуры.^[3][4]

• SPH можно легко распространить на широкий спектр областей и гибридизировать с некоторыми другими моделями, как обсуждается в Моделирование физики.
• Как обсуждалось в разделе о слабосжимаемый SPH, метод имеет отличные природоохранные свойства.
• Вычислительные затраты на моделирование SPH на количество частиц значительно меньше, чем затраты на сеточное моделирование на количество ячеек, когда интересующий показатель связан с жидкостью. плотность (например, функция плотности вероятности колебаний плотности).^[5] Дело в том, что в SPH разрешение ставится там, где дело.

Ограничения

• Установка граничных условий в SPH, таких как входы и выходы ^[6] и стены ^[7] это сложнее, чем с сеточными методами. Фактически, было заявлено, что «обработка граничных условий, безусловно, является одним из самых сложных технических моментов метода SPH».^[8] Эта проблема отчасти вызвана тем, что в SPH частицы вблизи границы меняются со временем.^[9] Тем не менее, стеновые граничные условия для SPH доступны. ^[7][9][10]
• Вычислительные затраты на моделирование SPH на количество частиц значительно превышают затраты на сеточное моделирование на количество ячеек, когда интересующая метрика не связана (напрямую) с плотностью (например, спектром кинетической энергии).^[5] Таким образом, игнорируя вопросы параллельного ускорение, моделирование течений постоянной плотности (например, внешних аэродинамика ) более эффективен с сеточными методами, чем с SPH.

Примеры

Динамика жидкостей

Рис. Моделирование океанских волн SPH с помощью FLUIDS v.1 (Hoetzlein)

Гидродинамика сглаженных частиц все чаще используется для моделирования движение жидкости также. Это связано с рядом преимуществ по сравнению с традиционными сетками. Во-первых, SPH гарантирует сохранение массы без дополнительных вычислений, поскольку сами частицы представляют собой массу. Во-вторых, SPH вычисляет давление на основе взвешенных вкладов соседних частиц, а не путем решения линейных систем уравнений. Наконец, в отличие от методов на основе сетки, которые должны отслеживать границы жидкости, SPH создает свободную поверхность для двухфазных взаимодействующих жидкостей напрямую, поскольку частицы представляют собой более плотную жидкость (обычно воду), а пустое пространство представляет более легкую жидкость (обычно воздух). По этим причинам можно моделировать движение жидкости с помощью SPH в реальном времени. Однако и методы на основе сетки, и методы SPH по-прежнему требуют создания визуализируемой геометрии свободной поверхности с использованием метода полигонизации, такого как метаболы и маршевые кубики, разбрызгивание точек, или «ковровая» визуализация. Для газовой динамики более целесообразно использовать саму функцию ядра для визуализации плотности газового столбца (например, как это делается в пакете визуализации SPLASH).

Одним из недостатков методов на основе сетки является необходимость большого количества частиц для моделирования с эквивалентным разрешением. В типичной реализации обоих равномерные сетки и методы частиц SPH, многие воксели или частицы будут использоваться для заполнения объемов воды, которые никогда не визуализируются. Однако точность может быть значительно выше с помощью сложных методов на основе сетки, особенно в сочетании с методами частиц (такими как наборы уровней частиц), поскольку легче обеспечить соблюдение условие несжимаемости в этих системах. SPH для моделирование жидкости все чаще используется в анимации в реальном времени и играх, где точность не так важна, как интерактивность.

Недавняя работа в SPH для моделирования жидкости повысила производительность, точность и области применения:

• Б. Соленталер, 2009, разрабатывает Predictive-Corrective SPH (PCISPH), чтобы учесть ограничения на несжимаемость.^[11]
• M. Ihmsen et al., 2010, представляют обработку границ и адаптивный временной шаг для PCISPH для точного взаимодействия с твердыми телами.^[12]
• K. Bodin et al., 2011, заменяют стандартное уравнение давления состояния ограничением плотности и применяют вариационный интегратор по времени^[13]
• R. Hoetzlein, 2012, разрабатывает эффективный SPH на базе графического процессора для больших сцен в Fluids v.3.^[14]
• N. Akinci et al., 2012, представляют универсальную обработку границ и технику двусторонней жесткой связи SPH, полностью основанную на гидродинамических силах; подход применим к разным типам решателей SPH ^[15]
• M. Macklin et al., 2013 моделируют потоки несжимаемой жидкости внутри структуры Position Based Dynamics для больших временных шагов. ^[16]
• N. Akinci et al., 2013, представляют универсальный метод поверхностного натяжения и двусторонней адгезии жидкость-твердое тело, позволяющий моделировать множество интересных физических эффектов, которые наблюдаются в реальности.^[17]
• J. Kyle и E. Terrell, 2013, применяют SPH для полнопленочной смазки.^[18]
• A. Mahdavi и N. Talebbeydokhti, 2015, предлагают гибридный алгоритм для реализации твердого граничного условия и моделирования потока через плотину с острым гребнем.^[19]
• S. Tavakkol et al., 2016, разработали curvSPH, который делает горизонтальный и вертикальный размер частиц независимыми и генерирует равномерное распределение массы вдоль криволинейных границ.^[20]
• W. Kostorz и A. Esmail-Yakas, 2020, предлагают общий, эффективный и простой метод оценки коэффициентов нормализации вблизи кусочно-плоских границ.^[10]

Астрофизика

Адаптивное разрешение гидродинамики сглаженных частиц, численное сохранение физически сохраняемых величин и способность моделировать явления, охватывающие многие порядки величины сделать его идеальным для вычислений в теоретическая астрофизика.^[21]

Моделирование формирование галактики, звездообразование, звездные столкновения,^[22] сверхновые^[23] и метеор Удары являются одними из самых разнообразных астрофизических и космологических применений этого метода.

SPH используется для моделирования гидродинамических потоков, включая возможные эффекты сила тяжести. Включение других важных астрофизических процессов, таких как перенос излучения и магнитные поля является активной областью исследований в астрономическом сообществе и имеет ограниченный успех.^[24][25]

Механика твердого тела

Либерский и Петчек^[26][27]расширил SPH на Механику твердого тела. Основным преимуществом SPH в этом приложении является возможность иметь дело с более значительными локальными искажениями, чем методы на основе сетки. Эта функция использовалась во многих приложениях в механике твердого тела: штамповка металла, удар, рост трещин, разрушение, фрагментация и т. Д.

Еще одно важное преимущество бессеточных методов в целом и SPH в частности состоит в том, что проблемы зависимости от сетки естественным образом можно избежать, учитывая бессеточный характер метода. В частности, выравнивание сетки связано с проблемами, связанными с трещинами, и его избегают в SPH из-за изотропной поддержки функций ядра. Однако классические составы SPH страдают нестабильностью при растяжении.^[28]и отсутствие последовательности.^[29]За последние годы были внесены различные поправки для повышения точности решения SPH, что привело к РКПМ Лю и др.^[30]Рэндлс и Либерский^[31]и Джонсон и Бейсель^[32]пытались решить проблему согласованности в своем исследовании ударных явлений.

Dyka et al.^[33][34]и Рэндлс и Либерски^[35]внедрили интеграцию точек напряжения в SPH и Тед Беличко и другие.^[36]показали, что метод точки напряжения устраняет нестабильность из-за ложных сингулярных мод, в то время как неустойчивости при растяжении можно избежать, используя лагранжевое ядро. В литературе можно найти множество других недавних исследований, посвященных улучшению сходимости метода SPH.

Недавние улучшения в понимании сходимости и стабильности SPH позволили найти более широкое применение в механике твердого тела. Другие примеры применения и развития метода включают:

• Моделирование обработки металлов давлением.^[37]
• Основанный на SPH метод SPAM (Smoothed Particle Applied Mechanics) для ударного разрушения твердых тел методом Уильям Г. Гувер.^[38]
• Модифицированный SPH (SPH / MLSPH) для разрушения и фрагментации.^[39]
• Taylor-SPH (TSPH) для распространения ударных волн в твердых телах.^[40]
• Обобщенная система координат SPH (GSPH) распределяет частицы неоднородно в декартовой системе координат и упорядочивает их посредством отображения в обобщенной системе координат, в которой частицы выровнены с одинаковым интервалом.^[41]

Числовые инструменты

Интерполяции

Метод гидродинамики сглаженных частиц (SPH) работает путем разделения жидкости на набор дискретных движущихся элементов. ${ displaystyle i, j}$, называемые частицами. Их лагранжева природа позволяет определить свою позицию ${ Displaystyle mathbf {r} _ {я}}$ интегрированием их скорости ${ Displaystyle mathbf {v} _ {я}}$ так как:

${ displaystyle { frac { mathrm {d} { boldsymbol {r}} _ {i}} { mathrm {d} t}} = { boldsymbol {v}} _ {i}.}$

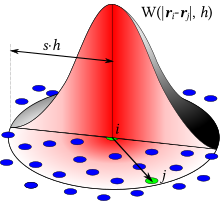
Эти частицы взаимодействуют через функция ядра с характеристическим радиусом, известным как «длина сглаживания», обычно представленным в уравнениях как ${ displaystyle h}$. Это означает, что физическое количество любой частицы может быть получено путем суммирования соответствующих свойств всех частиц, которые находятся в пределах диапазона ядра, причем последнее используется в качестве весовой функции. ${ displaystyle W}$. Это можно понять в два этапа. Сначала произвольное поле ${ displaystyle A}$ записывается как свертка с ${ displaystyle W}$:

${ displaystyle A ({ boldsymbol {r}}) = int A left ({ boldsymbol {r ^ { prime}}} right) W (| { boldsymbol {r}} - { boldsymbol { r ^ { prime}}} |, h) mathrm {d} V left ({ boldsymbol {r ^ { prime}}} right).}$

Ошибка в приведенном выше приближении порядка ${ displaystyle h ^ {2}}$. Во-вторых, интеграл аппроксимируется суммированием Римана по частицам:

${ displaystyle A ({ boldsymbol {r}}) = sum _ {j} V_ {j} A_ {j} W (| { boldsymbol {r}} - { boldsymbol {r}} _ {j} |, з),}$

где суммирование по ${ displaystyle j}$ включает все частицы в моделирование. ${ displaystyle V_ {j}}$ это объем частицы ${ displaystyle j}$, ${ displaystyle A_ {j}}$ это значение количества ${ displaystyle A}$ для частицы ${ displaystyle j}$ и ${ displaystyle { boldsymbol {r}}}$ обозначает позицию. Например, плотность ${ displaystyle rho _ {я}}$ частицы ${ displaystyle i}$ можно выразить как:

${ displaystyle rho _ {i} = rho ({ boldsymbol {r}} _ {i}) = sum _ {j} m_ {j} W_ {ij},}$

где ${ displaystyle m_ {j} = rho _ {j} V_ {j}}$ обозначает массу частицы, а ${ displaystyle rho _ {j}}$ плотность частиц, а ${ displaystyle W_ {ij} = W_ {ji}}$ это краткое обозначение ${ displaystyle W (| { boldsymbol {r}} _ {i} - { boldsymbol {r}} _ {j} |, h)}$. Погрешность аппроксимации интеграла дискретной суммой зависит от ${ displaystyle h}$, от размера частиц (т.е. ${ Displaystyle V_ {j} ^ {1 / d}}$, ${ displaystyle d}$ размерность пространства), а также расположение частиц в пространстве. О последнем эффекте пока мало что известно.^[42]

Обычно используемые функции ядра включают Функция Гаусса, то пятый шлиц и Вендланд ${ displaystyle C ^ {2}}$ ядро.^[43] Последние два ядра имеют компактный носитель (в отличие от гауссовского, где есть небольшой вклад на любом конечном расстоянии), с носителем, пропорциональным ${ displaystyle h}$. Это дает преимущество в экономии вычислительных затрат за счет исключения относительно незначительных вкладов от далеких частиц.

Хотя размер длины сглаживания можно фиксировать как в Космос и время, при этом не используются все возможности SPH. Назначая каждой частице собственную длину сглаживания и позволяя ей изменяться во времени, разрешение моделирования может автоматически адаптироваться в зависимости от местных условий. Например, в очень плотной области, где много частиц близко друг к другу, длина сглаживания может быть относительно короткой, что обеспечивает высокое пространственное разрешение. И наоборот, в областях с низкой плотностью, где отдельные частицы находятся далеко друг от друга и разрешение низкое, длину сглаживания можно увеличить, оптимизируя вычисления для интересующих областей.

Операторы

Для частиц постоянной массы, дифференцируя интерполированную плотность ${ displaystyle rho _ {я}}$ по времени дает

${ displaystyle { frac {d rho _ {i}} {dt}} = sum _ {j} m_ {j} left ({ boldsymbol {v}} _ {i} - { boldsymbol {v }} _ {j} right) cdot nabla W_ {ij},}$

где ${ displaystyle nabla W_ {ij} = - nabla W_ {ji}}$ это градиент ${ displaystyle W_ {ij}}$ относительно ${ displaystyle { boldsymbol {r}} _ {i}}$. Сравнивая приведенное выше уравнение с уравнением неразрывности в механика сплошной среды показывает, что правая часть является приближением ${ displaystyle - rho nabla cdot mathbf {v}}$; следовательно, оператор дискретной дивергенции определяется следующим образом:

${ displaystyle operatorname {D} _ {i} left {{ boldsymbol {v}} _ {j} right } = - { frac {1} { rho _ {i}}} sum _ {j} m_ {j} left ({ boldsymbol {v}} _ {i} - { boldsymbol {v}} _ {j} right) cdot nabla W_ {ij}.}$

Этот оператор дает SPH-приближение ${ Displaystyle набла cdot mathbf {v}}$ на частицу ${ displaystyle i}$ для данного набора частиц с заданными массами ${ displaystyle m_ {j}}$, должности ${ displaystyle left { mathbf {r} _ {j} right }}$ и скорости ${ displaystyle left { mathbf {v} _ {j} right }}$.

Точно так же можно определить оператор дискретного градиента, чтобы аппроксимировать градиент давления в положении частицы ${ displaystyle i}$:

${ displaystyle operatorname { mathbf {G}} _ {i} left {p_ {j} right } = { frac {1} { rho _ {i}}} sum _ {j} m_ {j} left ({ frac {p_ {i}} { rho _ {i} ^ {2}}} + { frac {p_ {j}} { rho _ {j} ^ {2}) }} right) nabla W_ {ij},}$

где ${ displaystyle left {p_ {j} right }}$ Обозначим набор давлений частиц. Есть несколько способов определить дискретные операторы в SPH; приведенные выше формулы расходимости и градиента обладают свойством быть кососопряженным, что приводит к хорошим свойствам сохранения.^[44] С другой стороны, в то время как оператор дивергенции ${ displaystyle operatorname {D}}$ согласована нулевого порядка, видно, что приближенный градиент ${ displaystyle operatorname { mathbf {G}}}$ это не так. Было предложено несколько методов для обхода этой проблемы, приводящих к перенормированным операторам (см., Например,^[45]).

Основные уравнения

Операторы SPH могут использоваться для дискретизации ряда дифференциальных уравнений в частных производных. Для сжимаемой невязкой жидкости Уравнения Эйлера о сохранении массы и балансе импульса читать:

${ displaystyle { frac {d rho} {dt}} = - rho nabla cdot { boldsymbol {v}}}$

${ displaystyle { frac {d { boldsymbol {v}}} {dt}} = - { frac {1} { rho}} nabla p + { boldsymbol {g}}}$

Все виды операторов дивергенции SPH и градиента практически можно использовать для целей дискретизации. Тем не менее, некоторые из них лучше справляются с физическими и численными эффектами. Часто используемая форма уравнений баланса основана на операторе симметричной дивергенции и антисимметричном градиенте:

${ displaystyle { frac {d rho _ {i}} {dt}} = - rho operatorname {D} _ {i} left {{ boldsymbol {v}} _ {j} right }}$

${ displaystyle { frac {d { boldsymbol {v}} _ {i}} {dt}} = - { frac {1} { rho}} operatorname { mathbf {G}} _ {i} left {p_ {j} right } + { boldsymbol {g}}}$

Хотя существует несколько способов дискретизации градиента давления в уравнениях Эйлера, приведенная выше антисимметричная форма является наиболее известной. Он поддерживает строгое сохранение линейного момента и момента количества движения. Это означает, что сила, действующая на частицу ${ displaystyle i}$ частичкой ${ displaystyle j}$ равно тому, которое действует на частицу ${ displaystyle j}$ частичкой ${ displaystyle i}$ включая изменение знака действующего направления, благодаря свойству антисимметрии ${ displaystyle nabla W_ {ij} = - nabla W_ {ji}}$.

Вариационный принцип

Приведенные выше управляющие уравнения SPH могут быть получены из Принцип наименьшего действия, начиная с Лагранжиан системы частиц:

${ displaystyle { mathcal {L}} = sum _ {j} m_ {j} left ({ tfrac {1} {2}} { boldsymbol {v}} _ {j} ^ {2} - e_ {j} + { boldsymbol {g}} cdot { boldsymbol {r}} _ {j} right)}$,

где ${ displaystyle e_ {j}}$ специфична ли частица внутренняя энергия. В Уравнение Эйлера – Лагранжа. вариационной механики для каждой частицы читается:

${ displaystyle { frac { mathrm {d}} { mathrm {d} t}} { frac { partial { mathcal {L}}} { partial { boldsymbol {v}} _ {i} }} = { frac { partial { mathcal {L}}} { partial { boldsymbol {r}} _ {i}}}.}.$

В применении к вышеуказанному лагранжиану он дает следующее уравнение импульса:

${ displaystyle { frac { mathrm {d} { boldsymbol {v}} _ {i}} { mathrm {d} t}} = - sum _ {j} m_ {j} { frac {p_ {j}} { rho _ {j} ^ {2}}} { frac { partial rho _ {j}} { partial rho _ {i}}} + { boldsymbol {g}}}$,

где мы использовали термодинамическое свойство ${ displaystyle mathrm {d} e = left (p / rho ^ {2} right) mathrm {d} rho}$. Добавление интерполяции плотности SPH и явное дифференцирование ${ displaystyle { tfrac { partial rho _ {j}} { partial rho _ {i}}}}$ приводит к

${ displaystyle { frac { mathrm {d} { boldsymbol {v}} _ {i}} { mathrm {d} t}} = - sum _ {j} m_ {j} left ({ frac {p_ {i}} { rho _ {i} ^ {2}}} + { frac {p_ {j}} { rho _ {j} ^ {2}}} right) nabla W_ { ij},}$

которое является уже упомянутым уравнением импульса SPH, в котором мы узнаем ${ displaystyle operatorname { mathbf {G}}}$ оператор. Это объясняет, почему сохраняется линейный импульс, а также позволяет сохранить угловой момент и энергию.^[46]

Интеграция времени

На основе работ, проделанных в 80-х и 90-х годах по численному интегрированию точечных частиц в больших ускорителях, были разработаны подходящие временные интеграторы с точными свойствами сохранения в долгосрочной перспективе; они называются симплектические интеграторы. Самым популярным в литературе SPH является чехарда схема, которая читается для каждой частицы ${ displaystyle i}$:

${ displaystyle { begin {align} { boldsymbol {v}} _ {i} ^ {n + 1/2} & = { boldsymbol {v}} _ {i} ^ {n} + { boldsymbol { a}} _ {i} ^ {n} { frac { Delta t} {2}}, { boldsymbol {r}} _ {i} ^ {n + 1} & = { boldsymbol {r }} _ {i} ^ {n} + { boldsymbol {v}} _ {i} ^ {i + 1/2} Delta t, { boldsymbol {v}} _ {i} ^ {n +1} & = { boldsymbol {v}} _ {i} ^ {n + 1/2} + { boldsymbol {a}} _ {i} ^ {i + 1} { frac { Delta t} {2}}, end {выравнивается}}}$

где ${ displaystyle Delta t}$ шаг по времени, верхний индекс обозначает итерацию по времени, а ${ Displaystyle { boldsymbol {а}} _ {я}}$ - ускорение частицы, заданное правой частью уравнения количества движения.

Существуют и другие симплектические интеграторы (см. Справочник ^[47]). Рекомендуется использовать симплектическую схему (даже низкого порядка) вместо несимплектической схемы высокого порядка, чтобы избежать накопления ошибок после многих итераций.

Интегрирование плотности мало изучено (см. ниже Больше подробностей).

Симплектические схемы консервативны, но явны, поэтому для их численной устойчивости требуются условия устойчивости, аналогичные условию Куранта-Фридрихса-Леви (см. ниже ).

Граничные техники

Поддержка SPH Convolution разделяется близко к границе

В случае, если свертка SPH должна практиковаться близко к границе, т.е. s · час, то интегральная опора обрезается. Действительно, когда на свертку влияет граница, свертка должна быть разбита на 2 интеграла:

${ displaystyle A ({ boldsymbol {r}}) = int _ { Omega ({ boldsymbol {r}})} A left ({ boldsymbol {r ^ { prime}}}} right) W (| { boldsymbol {r}} - { boldsymbol {r ^ { prime}}} |, h) d { boldsymbol {r ^ { prime}}} + int _ {B ({ boldsymbol { r}}) - Omega ({ boldsymbol {r}})} A left ({ boldsymbol {r ^ { prime}}} right) W (| { boldsymbol {r}} - { boldsymbol {r ^ { prime}}} |, h) d { boldsymbol {r ^ { prime}}},}$

где B (р) компактный опорный шар с центром в р, с радиусом s · час, и Ω (р) обозначает часть компактного носителя внутри расчетной области, Ω ∩ B (р). Следовательно, наложение граничных условий в SPH полностью основано на аппроксимации второго интеграла в правой части. То же самое, конечно, можно применить к вычислению дифференциальных операторов,

${ displaystyle nabla A ({ boldsymbol {r}}) = int _ { Omega ({ boldsymbol {r}})} A left ({ boldsymbol {r ^ { prime}}} right ) nabla W ({ boldsymbol {r}} - { boldsymbol {r ^ { prime}}}, h) d { boldsymbol {r ^ { prime}}} + int _ {B ({ boldsymbol {r}}) - Omega ({ boldsymbol {r}})} A left ({ boldsymbol {r ^ { prime}}} right) nabla W ({ boldsymbol {r}} - { boldsymbol {r ^ { prime}}}, h) d { boldsymbol {r ^ { prime}}}.}.}$

В прошлом для моделирования границ в SPH использовалось несколько методов.

Полное пренебрежение

Модель свободной поверхности SPH с помощью интегрального пренебрежения

Самая прямая граничная модель - это пренебрежение интегралом,

${ displaystyle int _ {B ({ boldsymbol {r}}) - Omega ({ boldsymbol {r}})} A left ({ boldsymbol {r ^ { prime}}}} right) набла W ({ boldsymbol {r}} - { boldsymbol {r ^ { prime}}}, h) d { boldsymbol {r ^ { prime}}} simeq { boldsymbol {0}},}$

такие, что учитываются только объемные взаимодействия,

${ displaystyle nabla A_ {i} = sum _ {j in Omega _ {i}} V_ {j} A_ {j} nabla W_ {ij}.}$

Это популярный подход, когда свободная поверхность рассматривается в однофазном моделировании.^[48]

Основное преимущество этого граничного условия - его очевидная простота. Однако при применении этого метода границ необходимо учитывать несколько вопросов согласованности.^[48] Фактически, это серьезное ограничение для его потенциальных приложений.

Расширение жидкости

SPH Fluid Extension Boundary техника

Вероятно, самый популярный или, по крайней мере, самый традиционный метод для наложения граничных условий в SPH - это метод расширения жидкости. Такой метод основан на заполнении компактной подложки через границу так называемыми фанатичными частицами с удобным наложением значений их полей.^[49]

Вдоль этой линии методология интегрального пренебрежения можно рассматривать как частный случай жидких расширений, когда поле, А, исчезают за пределами расчетной области.

Основное преимущество этой методологии - простота, при условии, что граничный вклад вычисляется как часть объемных взаимодействий. Кроме того, эта методология подверглась глубокому анализу в литературе.^[50][49][51]

С другой стороны, развертывание фантомных частиц в усеченной области - нетривиальная задача, так что моделирование сложных форм границ становится обременительным. Два наиболее популярных подхода к заполнению пустой области призрачными частицами - это зеркальные частицы. ^[52] и неподвижные частицы.^[49]

Граничный интеграл

Гранично-интегральная модель SPH

Новейшая пограничная техника - это методология граничного интеграла.^[53] В этой методологии интеграл пустого объема заменяется поверхностным интегралом и перенормировкой:

${ displaystyle nabla A_ {i} = { frac {1} { gamma _ {i}}} left ( sum _ {j in Omega _ {i}} V_ {j} A_ {j} nabla W_ {ij} + sum _ {j in partial Omega _ {i}} S_ {j} A_ {j} { boldsymbol {n}} _ {j} W_ {ij} right), }$

${ displaystyle gamma _ {i} = sum _ {j in Omega _ {i}} V_ {j} W_ {ij},}$

с участием п_j нормаль общего j^th граничный элемент. Поверхностный член также может быть решен с использованием полуаналитического выражения.^[53]

Моделирование физики

Гидродинамика

Слабо сжимаемый подход

Другой способ определения плотности основан на самом операторе сглаживания SPH. Следовательно, плотность оценивается по распределению частиц с использованием SPH. интерполяция. Чтобы преодолеть нежелательные ошибки на свободной поверхности из-за усечения ядра, формулировку плотности можно снова интегрировать во времени.^[53]

Слабо сжимаемый SPH в гидродинамике основан на дискретизации Уравнения Навье – Стокса или Уравнения Эйлера для сжимаемых жидкостей. Чтобы закрыть систему, соответствующий уравнение состояния используется для связи давления ${ displaystyle p}$ и плотность ${ displaystyle rho}$. Обычно так называемые Уравнение Коула^[54](иногда ошибочно называют "Уравнение Тэйта ") используется в SPH. Он читается как

${ displaystyle p = { frac { rho _ {0} c ^ {2}} { gamma}} left ( left ({ frac { rho} { rho _ {0}}} right ) ^ { gamma} -1 right) + p_ {0},}$

где ${ displaystyle rho _ {0}}$ эталонная плотность и ${ displaystyle c}$ то скорость звука. Для воды, ${ displaystyle gamma = 7}$ обычно используется. Фоновое давление ${ displaystyle p_ {0}}$ добавляется, чтобы избежать отрицательных значений давления.

Реальные почти несжимаемые жидкости, такие как вода, характеризуются очень высокой скоростью звука порядка ${ displaystyle 10 ^ {3} м / с}$. Следовательно, информация о давлении распространяется быстрее по сравнению с фактическим объемным потоком, что приводит к очень малым числам Маха. ${ displaystyle M}$. Уравнение количества движения приводит к следующему соотношению:

${ displaystyle { frac { delta rho} { rho _ {0}}} приблизительно { frac {| { boldsymbol {v}} |} {c ^ {2}}} = M ^ {2 }}$

где ${ displaystyle rho}$ изменение плотности и ${ displaystyle v}$ вектор скорости. На практике значение c меньше действительного, чтобы избежать слишком малых временных шагов в схеме интегрирования по времени. Обычно используется числовая скорость звука, при которой допускается изменение плотности менее 1%. Это так называемое предположение о слабой сжимаемости. число Маха меньше 0,1, что означает:

${ displaystyle c = 10v_ {max}}$

где максимальная скорость ${ displaystyle v_ {max}}$ необходимо оценить, например, по закону Торричелли или обоснованному предположению. Поскольку происходят только небольшие изменения плотности, можно принять линейное уравнение состояния:^[55]

${ displaystyle p = c ^ {2} left ( rho - rho _ {0} right)}$

Обычно слабосжимаемые схемы подвержены влиянию высокочастотных паразитных шумов на полях давления и плотности.^[56]Это явление вызвано нелинейным взаимодействием акустических волн и тем фактом, что схема является явной во времени и центрирована в пространстве.^[57]

На протяжении многих лет было предложено несколько методов избавления от этой проблемы. Их можно разделить на три разные группы:

1. схемы, использующие фильтры плотности,
2. модели, которые добавляют диффузный член в уравнение неразрывности,
3. схемы, которые используют решатели Римана для моделирования взаимодействия частиц.

Техника фильтрации плотности

В схемах первой группы фильтр применяется непосредственно к полю плотности для удаления паразитного числового шума. Наиболее часто используемые фильтры - это MLS (Moving Least Squares) и фильтр Шепарда. ^[56]который может применяться на каждом временном шаге или каждые n временных шагов. Чем чаще используется процедура фильтрации, тем более регулярные поля плотности и давления получаются, что, с другой стороны, приводит к увеличению вычислительных затрат. При длительном моделировании использование процедуры фильтрации может привести к нарушению составляющей гидростатического давления и несогласованности между глобальным объемом жидкости и полем плотности. Кроме того, это не гарантирует соблюдение динамической свободной поверхности. граничное условие.

Метод диффузного термина

Другой способ сгладить поля плотности и давления - добавить диффузный член в уравнение неразрывности (группа 2):

${ displaystyle { displaystyle { frac {d rho _ {i}} {dt}} = sum _ {j} m_ {j} left ({ boldsymbol {v}} _ {i} - { полужирный символ {v}} _ {j} right) cdot nabla W_ {ij} + { mathcal {D}} _ {i} ( rho),}}$

Первые схемы, использующие такой подход, были описаны в Ferrari.^[58]и в Мольтени^[55]где диффузионный член моделировался как лапласиан поля плотности. Аналогичный подход использовался и в ^[59].

Моделирование SPH: распределение давления потока при разрушении плотины с использованием стандартной постановки SPH

Моделирование SPH: распределение давления потока прорыва плотины с использованием стандартной формулы δ-SPH

В ^[60]поправка к диффузному члену Молтени^[55] было предложено устранить некоторые несоответствия вблизи свободной поверхности. В этом случае принятый диффузионный член эквивалентен дифференциальному оператору высокого порядка на поле плотности.^[61]Схема называется δ-SPH и сохраняет все свойства сохранения SPH без диффузии (например, линейный и угловой моменты, полную энергию, см. ^[62]) наряду с гладким и регулярным представлением полей плотности и давления.

В третью группу входят схемы SPH, в которых используются числовые потоки, полученные с помощью решателей Римана, для моделирования взаимодействий частиц. ^[63][64][65].

Метод решателя Римана

Моделирование SPH: распределение давления потока прорыва плотины с использованием решателя Римана с ограничителем малой диссипации.

Для метода SPH, основанного на решателях Римана, межчастичная задача Римана строится по единичному вектору${ displaystyle { mathbf {e}} _ {ij} = - { mathbf {r}} _ {ij} / r_ {ij}}$ указывающая форма частицы ${ displaystyle i}$ частицы ${ displaystyle j}$. В этой задаче Римана начальные левое и правое состояния находятся на частицах${ displaystyle i}$ и ${ displaystyle j}$ соответственно. В ${ displaystyle L}$ и ${ displaystyle R}$ государства

${ displaystyle { begin {case} ( rho _ {L}, U_ {L}, P_ {L}) = ( rho _ {i}, { mathbf {v}} _ {i} cdot { mathbf {e}} _ {ij}, P_ {i}) ( rho _ {R}, U_ {R}, P_ {R}) = ( rho _ {j}, { mathbf {v }} _ {j} cdot { mathbf {e}} _ {ij}, P_ {j}) end {ases}}.}$

Решение задачи Римана приводит к трем волнам, исходящим от разрыва. Две волны, которые могут быть ударной волной или волной разрежения, распространяются с наименьшей или наибольшей скоростью волны. Средняя волна всегда является контактным разрывом и разделяет два промежуточных состояния, обозначаемых ${ displaystyle ( rho _ {L} ^ { ast}, U_ {L} ^ { ast}, P_ {L} ^ { ast})}$ и${ displaystyle ( rho _ {R} ^ { ast}, U_ {R} ^ { ast}, P_ {R} ^ { ast})}$. Предполагая, что промежуточное состояние удовлетворяет${ Displaystyle U_ {L} ^ { ast} = U_ {R} ^ { ast} = U ^ { ast}}$и ${ Displaystyle P_ {L} ^ { ast} = P_ {R} ^ { ast} = P ^ { ast}}$, линеаризованный решатель Римана для гладких течений или только с умеренно сильными ударами может быть записан как

${ displaystyle { begin {cases} U ^ { ast} = { overline {U}} + { frac {1} {2}} { frac {(P_ {L} -P_ {R})} {{ bar { rho}} c_ {0}}} P ^ { ast} = { overline {P}} + { frac {1} {2}} { bar { rho}} c_ {0} {(U_ {L} -U_ {R})} end {cases}},}$

где ${ Displaystyle { overline {U}} = (U_ {L} + U_ {R}) / 2}$ и ${ Displaystyle { overline {P}} = (P_ {L} + P_ {R}) / 2}$- средние значения между частицами. При решении проблемы Римана, т.е. ${ Displaystyle U ^ { ast}}$ и ${ Displaystyle P ^ { ast}}$, дискретизация метода SPH равна

${ displaystyle { frac {d rho _ {i}} {dt}} = 2 rho _ {i} sum _ {j} { frac {m_ {j}} { rho _ {j}} } ({ mathbf {v}} _ {i} - { mathbf {v}} ^ { ast}) cdot nabla _ {i} W_ {ij},}$

${ displaystyle { frac {d { mathbf {v}} _ {i}} {dt}} = - 2 sum _ {j} m_ {j} { bigg (} { frac {P ^ { ast}} { rho _ {i} rho _ {j}}} { bigg)} nabla _ {i} W_ {ij}.}$

где ${ displaystyle { mathbf {v}} ^ { ast} = U ^ { ast} { mathbf {e}} _ {ij} + ({ overline { mathbf {v}}} _ {ij} - { overline {U}} { mathbf {e}} _ {ij})}$Это указывает на то, что средняя скорость и давление между частицами просто заменяются решением задачи Римана. Сравнивая и то и другое, можно видеть, что промежуточные скорость и давление из средних значений между частицами составляют неявную диссипацию, то есть регуляризацию плотности. и числовая вязкость соответственно.

Поскольку вышеупомянутая дискретизация является очень диссипативной, прямой модификацией является применение ограничителя для уменьшения неявных численных диссипаций, вводимых путем ограничения промежуточного давления с помощью^[66]

${ displaystyle P ^ { ast} = { overline {P}} + { frac {1} {2}} beta { overline { rho}} {(U_ {L} -U_ {R}) },}$

где ограничитель определяется как

${ displaystyle beta = min { big (} eta max (U_ {L} -U_ {R}, 0), { overline {c}} { big)}.}$

Обратите внимание, что ${ displaystyle beta}$ гарантирует отсутствие диссипации, когда жидкость находится под действием волны расширения, т.е. ${ Displaystyle U_ {L}$, и что параметр ${ displaystyle eta}$, используется для модуляции диссипации, когда жидкость находится под действием волны сжатия, т.е. ${ Displaystyle U_ {L} geq U_ {R}}$. Численные эксперименты показали, что ${ displaystyle eta = 3}$ в целом эффективен. Также обратите внимание, что диссипация, вносимая промежуточной скоростью, не ограничена.

Несжимаемый подход

Моделирование вязкости

В общем, описание гидродинамических течений требует удобного рассмотрения диффузионных процессов для моделирования вязкость в Уравнения Навье – Стокса. Это требует особого рассмотрения, поскольку включает в себя лапласианин дифференциальный оператор. Поскольку прямые вычисления не дают удовлетворительных результатов, было предложено несколько подходов к моделированию диффузии.

• Искусственная вязкость

Представлено Monaghan и Gingold^[67]искусственная вязкость использовалась для борьбы с высокими число Маха потоки жидкости. Он читает

${ displaystyle Pi _ {ij} = { begin {case} displaystyle { frac {- alpha { bar {c}} _ {ij} phi _ {ij} + beta phi _ {ij } ^ {2}} {{ bar { rho}} _ {ij}}} & quad { boldsymbol {v}} _ {ij} cdot { boldsymbol {r}} _ {ij} <0 0 & quad { boldsymbol {v}} _ {ij} cdot { boldsymbol {r}} _ {ij} geq 0 end {case}}}$

Вот, ${ displaystyle alpha}$ контролирует объемную вязкость, пока ${ displaystyle beta}$ действует аналогично искусственной вязкости Neumann Richtmeyr. В ${ displaystyle phi _ {ij}}$ определяется

${ displaystyle phi _ {ij} = { frac {h { boldsymbol {v}} _ {ij} cdot { boldsymbol {r}} _ {ij}} { Vert { boldsymbol {r}} _ {ij} Vert ^ {2} + eta _ {h} ^ {2}}}.}.$

Также было показано, что искусственная вязкость улучшает общую стабильность моделирования потока. Таким образом, он применяется к невязким проблемам в следующей форме

${ displaystyle Pi _ {ij} = alpha hc { frac {{ boldsymbol {v}} _ {ij} cdot { boldsymbol {r}} _ {ij}} { Vert { boldsymbol {r }} _ {ij} Vert ^ {2} + eta _ {h} ^ {2}}}.}.}$

С помощью этого подхода можно не только стабилизировать невязкое моделирование, но и смоделировать физическую вязкость. Сделать так

${ displaystyle alpha hc = 2 (n + 2) { frac { mu} { rho}}}$

подставляется в уравнение выше, где ${ displaystyle n}$ - количество пространственных размеров модели. Этот подход вводит объемную вязкость ${ displaystyle zeta = { frac {5} {3}} mu}$.

• Моррис

Для низкого Числа Рейнольдса модель вязкости Морриса^[68]было предложено.

${ displaystyle [ nu Delta { boldsymbol {v}}] _ {ij} = { frac {2 nu} { rho _ {j}}} , { frac {{ boldsymbol {r} } _ {ij} cdot nabla w_ {h, ij}} { Vert { boldsymbol {r}} _ {ij} Vert ^ {2} + eta _ {h} ^ {2}}} , { boldsymbol {v}} _ {ij}.}$

• LoShao

Дополнительная физика

• Поверхностное натяжение
• Теплопередача
• Турбулентность

Многофазные расширения

Астрофизика

Часто в астрофизике в дополнение к чистой гидродинамике хотят моделировать самогравитацию. Основанная на частицах природа SPH делает его идеальным для сочетания с гравитационным решателем на основе частиц, например код силы тяжести дерева,^[69] сетка частиц, или частица-частица-сетка.

Механика твердого тела и взаимодействие жидкости и структуры (FSI)

Полная лагранжева формулировка механики твердого тела

Для дискретизации основных уравнений динамики твердого тела используется корректирующая матрица ${ displaystyle mathbb {B} ^ {0}}$ ^[70][71]впервые вводится для воспроизведения вращения твердого тела как

${ displaystyle mathbb {B} _ {a} ^ {0} = left ( sum _ {b} V_ {b} ^ {0} left ( mathbf {r} _ {b} ^ {0}) - mathbf {r} _ {a} ^ {0} right) otimes nabla _ {a} ^ {0} W_ {ab} right) ^ {- 1}}$

(1)

где

${ displaystyle nabla _ {a} ^ {0} W_ {a} = { frac { partial W left (| mathbf {r} _ {ab} ^ {0} |, h right)} { partial | mathbf {r} _ {ab} ^ {0} |}} mathbf {e} _ {ab} ^ {0}}$

обозначает градиент функции ядра, вычисленный в начальной эталонной конфигурации. Обратите внимание, что индексы ${ displaystyle a}$ и ${ displaystyle b}$ используются для обозначения твердых частиц, а длина сглаживания ${ displaystyle h}$ идентична дискретизации уравнений жидкости.

Используя исходную конфигурацию в качестве эталона, плотность твердого тела непосредственно оценивается как

${ displaystyle rho _ {a} = rho _ {a} ^ {0} { frac {1} {J}}}$

(2)

где ${ Displaystyle J = Det ( mathbb {F})}$ - определитель Якоби тензора деформации ${ Displaystyle mathbb {F}}$.

Теперь мы можем дискретизировать уравнение импульса в следующем виде

${ displaystyle m_ {a} { frac {{ text {d}} mathbf {v}} {{ text {d}} t}} = 2 sum _ {b} V_ {a} V_ {b } { tilde { mathbb {P}}} _ {ab} nabla _ {a} ^ {0} W_ {ab} + mathbf {g} + mathbf {f} _ {a} ^ {F: p} + mathbf {f} _ {a} ^ {F: v}}$

(3)

где среднее между частицами первое напряжение Пиолы-Кирхгофа ${ Displaystyle { тильда { mathbb {P}}}}$ определяется как

${ displaystyle { tilde { mathbb {P}}} _ {ab} = { frac {1} {2}} left ( mathbb {P} _ {a} mathbb {B} _ {a} ^ {0} + mathbb {P} _ {b} mathbb {B} _ {b} ^ {0} right)}$

(4)

.

Также ${ displaystyle mathbf {f} _ {a} ^ {F: p}}$ и ${ displaystyle mathbf {f} _ {a} ^ {F: v}}$ соответствуют давлению жидкости и силам вязкости, действующим на твердую частицу ${ displaystyle a}$соответственно.

Муфта структура жидкости

При взаимодействии жидкость-конструкция окружающая твердая структура ведет себя как движущаяся граница для жидкости, и на границе раздела жидкость-конструкция накладывается граничное условие прилипания. ${ displaystyle mathbf {f} _ {i} ^ {S: p}}$ и ${ displaystyle mathbf {f} _ {i} ^ {S: v}}$ действуя на жидкую частицу ${ displaystyle i}$, из-за наличия соседней твердой частицы ${ displaystyle a}$, можно получить как

${ displaystyle mathbf {f} _ {i} ^ {S: p} = - 2 sum _ {a} V_ {i} V_ {a} { frac {p_ {i} rho _ {a} ^ {d} + p_ {a} ^ {d} rho _ {i}} { rho _ {i} + rho _ {a} ^ {d}}} nabla _ {i} W ( mathbf { r} _ {ia}, h)}$

(5)

и

${ displaystyle mathbf {f} _ {i} ^ {S: v} = 2 sum _ {a} eta V_ {i} V_ {a} { frac { mathbf {v} _ {i} - mathbf {v} _ {a} ^ {d}} {r_ {ia}}} { frac { partial W ( mathbf {r} _ {ia}, h)} { partial {{r} _ {ia}}}}}$

(6)

.

Здесь мнимое давление ${ displaystyle p_ {a} ^ {d}}$ и скорость ${ displaystyle mathbf {v} _ {a} ^ {d}}$ определены

${ displaystyle { begin {cases} p_ {a} ^ {d} = p_ {i} + rho _ {i} max (0, ( mathbf {g} - { frac {{ text {d}) } mathbf {v} _ {a}} {{ text {d}} t}}) cdot mathbf {n} ^ {S}) ( mathbf {r} _ {ia} cdot mathbf { n} ^ {S}) mathbf {v} _ {a} ^ {d} = 2 mathbf {v} _ {i} - mathbf {v} _ {a} end {cases}}}$

(7)

.

где ${ Displaystyle mathbf {п} ^ {S}}$ обозначает направление нормали к поверхности твердой структуры, а мнимая плотность частиц ${ displaystyle rho _ {a} ^ {d}}$ рассчитывается через уравнение состояния.

Соответственно силы взаимодействия ${ displaystyle mathbf {f} _ {a} ^ {F: p}}$ и ${ displaystyle mathbf {f} _ {a} ^ {F: v}}$ действуя на твердую частицу ${ displaystyle a}$ даны

${ displaystyle mathbf {f} _ {a} ^ {F: p} = - 2 sum _ {i} V_ {a} V_ {i} { frac {p_ {a} ^ {d} rho _ {i} + p_ {i} rho _ {a} ^ {d}} { rho _ {i} + rho _ {a} ^ {d}}} nabla _ {a} W ( mathbf { r} _ {ai}, h)}$

(8)

и

${ displaystyle mathbf {f} _ {a} ^ {F: v} = 2 sum _ {i} eta V_ {a} V_ {i} { frac { mathbf {v} _ {a} ^ {d} - mathbf {v} _ {i}} {r_ {ia}}} { frac { partial W ( mathbf {r} _ {ia}, h)} { partial {{r} _ {ai}}}}}$

(9)

.

Антисимметричное свойство производной ядерной функции обеспечит сохранение импульса для каждой пары взаимодействующих частиц ${ displaystyle i}$ и ${ displaystyle a}$.

Другие

В метод дискретных элементов, используется для моделирования сыпучие материалы, относится к SPH.

Варианты метода

Этот раздел пуст. Вы можете помочь добавляя к этому. (Июль 2018 г.)

использованная литература

дальнейшее чтение

• Гувер, В. Г. (2006). Прикладная механика гладких частиц: состояние дел, мировая наука.
• Моделирование удара с помощью SPH Стеллингверф Р.Ф., Вингейт К.А., Memorie della Societa Astronomia Italiana, Vol. 65, стр. 1117 (1994).
• Amada, T., Imura, M., Yasumuro, Y., Manabe, Y. и Chihara, K. (2004) Моделирование жидкости на основе частиц на GPU, в материалах семинара ACM по универсальным вычислениям на графических процессорах (август , 2004, Лос-Анджелес, Калифорния).
• Дебрун М. и Кани М.П. (1996). Smoothed Particles: новая парадигма анимации сильно деформируемых тел. В материалах семинара Eurographics по компьютерной анимации и моделированию (август 1996 г., Пуатье, Франция).
• Хегеман К., Карр Н.А. и Миллер Г.С.П. Моделирование жидкости на основе частиц на графическом процессоре. В материалах Международной конференции по вычислительной науке (Ридинг, Великобритания, май 2006 г.). Труды опубликованы как Lecture Notes in Computer Science v. 3994/2006 (Springer-Verlag).
• М. Келагер. (2006) Лагранжева гидродинамика с использованием гидродинамики сглаженных частиц, М. Келагар (докторская диссертация, Университет Копенгагена).
• Колб А. и Кунц Н. (2005). Динамическое связывание частиц для моделирования жидкости на базе графического процессора. В материалах 18-го симпозиума по методам моделирования (2005), стр. 722–727.
• Лю, Г. и Лю, М. Гидродинамика сглаженных частиц: метод частиц без сетки. Сингапур: World Scientific (2003).
• Монаган, Дж. Дж. (1992). Гидродинамика сглаженных частиц. Анну. Rev. Astron. Astrophys. (1992). 30: 543–74.
• Мюллер, М., Чарипар, Д. и Гросс, М. Моделирование жидкостей на основе частиц для интерактивных приложений, В трудах симпозиума Eurographics / SIGGRAPH по компьютерной анимации (2003), ред. Д. Брин и М. Лин.
• Вестерлунд М. Моделирование и визуализация вязкой жидкости с использованием гидродинамики сглаженных частиц (диплом магистра, Университет Умео, Швеция).
• Виоло Д. Механика жидкости и метод SPH. Издательство Оксфордского университета (2012).

внешние ссылки

• Первое крупное моделирование звездообразования с использованием SPH
• СФЕРИКА (Международное Сообщество Исследователей и Разработки SPH)
• ITVO - это веб-сайт Итальянской теоретической виртуальной обсерватории, созданный для запроса базы данных архива численного моделирования.
• Галерея изображений SPHC изображает широкий спектр тестовых примеров, экспериментальных проверок и коммерческих приложений SPH-кода SPHC.
• Вывод модели SPH, исходя из уравнений Навье-Стокса.

Программного обеспечения

• Algodoo - это 2D-симулятор для обучения с использованием SPH
• АКВАгпусф это бесплатный (GPLv3) SPH исследователей, от исследователей, для исследователей
• решения для дайвинга это коммерческое программное обеспечение для проектирования SPH на базе Интернета для целей CFD
• DualSPHysics - это в основном код SPH с открытым исходным кодом, основанный на SPHysics и использующий вычисления на GPU. Компоненты с открытым исходным кодом доступны по лицензии LGPL.
• ЖИДКОСТЬ v.1 - это простая реализация 3D SPH с открытым исходным кодом (Zlib) в реальном времени на C ++ для жидкостей для CPU и GPU.
• Fluidix представляет собой API моделирования частиц на основе графического процессора, доступный в OneZero Software
• ГАДЖЕТ [1] свободно доступный (GPL ) код для космологического моделирования N-тела / SPH
• GPUSPH Симулятор SPH с вязкостью (GPLv3)
• Pasimodo представляет собой программный пакет для методов моделирования на основе частиц, например SPH
• Слой абстракции физики это система абстракции с открытым исходным кодом, которая поддерживает движки физики в реальном времени с поддержкой SPH
• PreonLab это программное обеспечение для коммерческого проектирования, разработанное Технология FIFTY2 реализация неявного метода SPH
• Пунто это свободно доступный инструмент визуализации для моделирования частиц
• pysph Платформа с открытым исходным кодом для гидродинамики сглаженных частиц в Python (новая лицензия BSD)
• RealFlow Коммерческий SPH-решатель для киноиндустрии.
• SimPARTIX это коммерческий пакет моделирования для SPH и Метод дискретных элементов (DEM) моделирование из Fraunhofer IWM
• SPH-поток
• СФЕРА
• SPHinXsys - это мультифизическая библиотека SPH с открытым исходным кодом и несколькими разрешениями. Он предоставляет API-интерфейсы C ++ для точного физического моделирования и нацелен на моделирование связанных промышленных динамических систем, включая динамику жидкости, твердого тела, динамики нескольких тел и других.
• SPHysics это реализация SPH с открытым исходным кодом на Фортране
• Брызги это инструмент визуализации с открытым исходным кодом (GPL) для моделирования SPH
• СИМПЛЕР: Бесплатный симулятор SYMbolic ParticLE от Университета Фрайбурга.
• Nauticle представляет собой универсальный вычислительный инструмент для численных методов на основе частиц.