Скорость звука - Википедия - Speed of sound

В скорость звука расстояние, пройденное за единицу времени звуковая волна поскольку он распространяется через эластичный средний. При 20 ° C (68 ° F) скорость звука в воздухе составляет около 343 метров в секунду (1235 км / ч; 1125 футов / с; 767 миль / ч; 667 узлов), или километр в 2,9 с или миля в 4,7 с. Это сильно зависит от температуры, а также от среды, через которую звуковая волна распространяется.

Скорость звука в идеальный газ зависит только от его температуры и состава. Скорость имеет слабую зависимость от частоты и давления в обычном воздухе, немного отклоняясь от идеального поведения.

В разговорной речи скорость звука относится к скорости звуковых волн в воздуха. Однако скорость звука варьируется от вещества к веществу: обычно звук распространяется медленнее всего в газы, быстрее в жидкости, и еще быстрее в твердые вещества. Например, хотя, как отмечалось выше, звук распространяется на 343 м / с в воздухе, он путешествует на 1481 м / с в воды (почти в 4,3 раза быстрее) и на 5120 м / с в железе (почти в 15 раз быстрее). В исключительно жестком материале, таком как алмаз, звук распространяется со скоростью 12 000 метров в секунду (39 000 футов / с),^[1]- примерно в 35 раз быстрее его скорости в воздухе и примерно так же быстро, как в обычных условиях.

Звуковые волны в твердых телах состоят из волн сжатия (так же, как в газах и жидкостях), и звуковой волны другого типа, называемой поперечная волна, что встречается только в твердых телах. Сдвиговые волны в твердых телах обычно распространяются с разными скоростями, как показано на сейсмология. Скорость волн сжатия в твердых телах определяется величиной среды сжимаемость, модуль сдвига и плотность. Скорость поперечных волн определяется только модулем сдвига и плотностью твердого материала.

В динамика жидкостей скорость звука в текучей среде (газе или жидкости) используется в качестве относительной меры скорости объекта, движущегося в среде. Отношение скорости объекта к скорости звука в жидкости называется величиной объекта. число Маха. Объекты движутся со скоростью более Мах1 говорят, путешествуют в сверхзвуковой скорости.

История

Сэр Исаак Ньютон 1687 год Principia включает вычисление скорости звука в воздухе как 979 футов в секунду (298 м / с). Это слишком мало примерно на 15%.^[2] Несоответствие в первую очередь связано с пренебрежением (тогда неизвестным) эффектом быстро меняющейся температуры в звуковой волне (в современных терминах сжатие и расширение воздуха звуковой волной - это адиабатический процесс, а не изотермический процесс ). Позднее эта ошибка была исправлена Лаплас.^[3]

В течение 17 века было несколько попыток точно измерить скорость звука, включая попытки Марин Мерсенн в 1630 году (1380 парижских футов в секунду), Пьер Гассенди в 1635 году (1473 парижских фута в секунду) и Роберт Бойл (1125 парижских футов в секунду).^[4] В 1709 году преподобный Уильям Дерхам, Ректор компании Upminster опубликовали более точные данные о скорости звука: 1072 Парижские ноги в секунду.^[4] (The Парижская стопа было 325 мм. Это длиннее стандартного «международного фута», широко используемого сегодня, который был официально определен в 1959 году как 304,8 мм, что означает скорость звука при 20 ° C (68 ° F) 1055 парижских футов в секунду).

Дерхам использовал телескоп с башни церковь Святого Лаврентия, Апминстер наблюдать за вспышкой выстрела из дробовика на расстоянии, а затем измерял время, пока он не услышал выстрел, с помощью полсекундного маятника. Были произведены замеры выстрелов из ряда местных достопримечательностей, в том числе North Ockendon церковь. Расстояние было известно триангуляция, и таким образом была вычислена скорость, с которой распространялся звук.^[5]

Базовые концепты

Передачу звука можно проиллюстрировать с помощью модели, состоящей из множества сферических объектов, связанных между собой пружинами.

В реальных материальных условиях сферы представляют молекулы материала, а пружины представляют собой облигации между ними. Звук проходит через систему, сжимая и расширяя пружины, передавая акустическую энергию соседним сферам. Это помогает передавать энергию, в свою очередь, пружинам (связям) соседней сферы и так далее.

Скорость звука через модель зависит от жесткость / жесткость пружины, и масса сфер. Пока расстояние между сферами остается постоянным, более жесткие пружины / связи передают энергию быстрее, в то время как более крупные сферы передают энергию медленнее.

В реальном материале жесткость пружин известна как "модуль упругости ", а масса соответствует материалу плотность. Учитывая, что при прочих равных (при прочих равных условиях ) звук будет медленнее губчатые материалы и быстрее в более жестких. Такие эффекты, как дисперсия и отражение, также можно понять с помощью этой модели.^{[нужна цитата ]}

Например, звук в никеле распространяется в 1,59 раза быстрее, чем в бронзе, из-за большей жесткости никеля примерно при такой же плотности. Точно так же звук распространяется примерно в 1,41 раза быстрее в легком водороде (протий ) газ, чем в тяжелом водороде (дейтерий ) газ, поскольку дейтерий имеет аналогичные свойства, но в два раза большую плотность. В то же время звук «компрессионного типа» будет распространяться быстрее в твердых телах, чем в жидкостях, и быстрее в жидкостях, чем в газах, потому что твердые тела сложнее сжимать, чем жидкости, а жидкости, в свою очередь, труднее сжимать. чем газы.

В некоторых учебниках ошибочно утверждается, что скорость звука увеличивается с плотностью. Это понятие проиллюстрировано представлением данных для трех материалов, таких как воздух, вода и сталь, каждый из которых имеет существенно разную сжимаемость, что более чем компенсирует разницу в плотности. Наглядным примером этих двух эффектов является то, что звук в воде распространяется всего в 4,3 раза быстрее, чем в воздухе, несмотря на огромные различия в сжимаемости двух сред. Причина в том, что большая плотность воды, которая работает на медленный звук в воде по сравнению с воздухом почти компенсирует разницу в сжимаемости двух сред.

Практический пример можно наблюдать в Эдинбурге, когда "One o'Clock Gun" стреляют в восточной части Эдинбургского замка. Стоя у подножия западной оконечности Касл-Рока, звук ружья можно услышать сквозь скалу, незадолго до того, как он прибудет по воздуху, частично задержанный немного более длинным маршрутом. Это особенно эффективно, если производится салют из нескольких пистолетов, например, "День рождения королевы".

Сжатие и поперечные волны

Импульс давления или волна сжатия (продольная волна ) приурочен к плоскости. Это единственный тип звуковой волны, которая распространяется в жидкостях (газах и жидкостях). Волна типа давления может также распространяться в твердых телах вместе с другими типами волн (поперечные волны, Смотри ниже)

Поперечная волна воздействуя на атомы, изначально ограниченные плоскостью. Этот дополнительный тип звуковой волны (дополнительный тип упругой волны) распространяется только в твердых телах, так как он требует поперечного сдвигающего движения, которое поддерживается наличием упругости в твердом теле. Боковое срезание может происходить в любой направление, которое находится под прямым углом к ​​направлению распространения волны (здесь показано только одно направление сдвига под прямым углом к ​​плоскости). Кроме того, направление сдвига под прямым углом может меняться со временем и на расстоянии, что приводит к различным типам поляризация поперечных волн

В газе или жидкости звук состоит из волн сжатия. В твердых телах волны распространяются двух разных типов. А продольная волна связан со сжатием и декомпрессией в направлении движения, и является одним и тем же процессом в газах и жидкостях, с аналогичной волной сжатия в твердых телах. В газах и жидкостях поддерживаются только волны сжатия. Дополнительный тип волны - поперечная волна, также называемый поперечная волна, встречается только в твердых телах, поскольку только твердые тела поддерживают упругие деформации. Это связано с упругой деформацией среды перпендикулярно направлению распространения волны; направление деформации сдвига называется "поляризация "этого типа волн. Обычно поперечные волны возникают как пара ортогональный поляризации.

Эти разные волны (волны сжатия и разные поляризации поперечных волн) могут иметь разные скорости на одной и той же частоте. Следовательно, они приходят к наблюдателю в разное время, крайним примером является землетрясение, где сначала приходят резкие волны сжатия, а секунды спустя - колебательные поперечные волны.

Скорость волны сжатия в жидкости определяется ее сжимаемость и плотность. В твердых телах волны сжатия аналогичны волнам в жидкостях, в зависимости от сжимаемости и плотности, но с дополнительным фактором модуль сдвига которая влияет на волны сжатия из-за внеосевой упругой энергии, которая может влиять на эффективное растяжение и релаксацию при сжатии. Скорость сдвиговых волн, которые могут возникать только в твердых телах, определяется просто модулем сдвига и плотностью твердого материала.

Уравнения

Скорость звука в математических обозначениях условно обозначается как c, от латинского Celeritas что означает «скорость».

Для жидкостей в целом скорость звука c дается уравнением Ньютона – Лапласа:

${ displaystyle c = { sqrt { frac {K_ {s}} { rho}}},}$

куда

• K_s - коэффициент жесткости, изоэнтропический объемный модуль (или модуль объемной упругости для газов);
• ${ displaystyle rho}$ это плотность.

Таким образом, скорость звука увеличивается с увеличением жесткости (сопротивления упругого тела деформации под действием приложенной силы) материала и уменьшается с увеличением плотности. Для идеальных газов модуль объемной упругости K это просто давление газа, умноженное на безразмерное индекс адиабаты, что составляет около 1,4 для воздуха при нормальных условиях давления и температуры.

Для общего уравнения состояния, если классическая механика используется скорость звука c можно вывести^[6] следующее:

Рассмотрим звуковую волну, распространяющуюся по трубе с площадью поперечного сечения ${ displaystyle A}$. Во временном интервале ${ displaystyle dt}$ он движется по трубке длиной ${ displaystyle dz = vdt}$. В устойчивое состояние, то массовый расход ${ displaystyle { dot {m}} = rho vA}$ должны быть одинаковыми на двух концах трубки, поэтому массовый поток ${ displaystyle j = rho v = const. , rightarrow vd rho = - rho dv}$. За Второй закон Ньютона, то сила градиента давления обеспечивает ускорение:

${ displaystyle { begin {align} { frac {dv} {dt}} & = - { frac {1} { rho}} { frac {dp} {dz}} rightarrow dp & = ( - rho dv) { frac {dz} {dt}} = (vd rho) v rightarrow v ^ {2} & Equiv c ^ {2} = { frac {dp} {d rho }} end {выровнены}}}$

И поэтому:

${ displaystyle c = { sqrt { left ({ frac { partial p} { partial rho}} right) _ {s}}},}$

куда

• п давление;
• ${ displaystyle rho}$ это плотность и производная берется изэнтропически, то есть при постоянном энтропия s. Это потому, что звуковая волна распространяется так быстро, что ее распространение можно представить как адиабатический процесс.

Если релятивистский эффекты важны, скорость звука рассчитывается из релятивистские уравнения Эйлера.

В недисперсная среда, скорость звука не зависит от частота звука, поэтому скорости переноса энергии и распространения звука одинаковы для всех частот. Воздух, смесь кислорода и азота, представляет собой недиспергирующую среду. Однако воздух действительно содержит небольшое количество CO.₂ который является диспергирующая среда и вызывает диспергирование в воздухе при ультразвуковой частоты (> 28 кГц).^[7]

В дисперсионная среда скорость звука является функцией звуковой частоты, через соотношение дисперсии. Каждая частотная составляющая распространяется со своей скоростью, называемой фазовая скорость, а энергия возмущения распространяется на групповая скорость. То же самое происходит со световыми волнами; видеть оптическая дисперсия для описания.

Зависимость от свойств среды

Скорость звука переменна и зависит от свойств вещества, через которое распространяется волна. В твердых телах скорость поперечных (или поперечных) волн зависит от деформации сдвига под действием напряжения сдвига (называемого модуль сдвига ) и плотности среды. Продольные волны (или волны сжатия) в твердых телах зависят от тех же двух факторов с добавлением зависимости от сжимаемость.

В жидкостях важными факторами являются только сжимаемость и плотность среды, поскольку жидкости не передают напряжения сдвига. В гетерогенных средах, таких как жидкость, заполненная пузырьками газа, плотность жидкости и сжимаемость газа аддитивно влияют на скорость звука, как показано на эффект горячего шоколада.

В газах адиабатическая сжимаемость напрямую связана с давлением через коэффициент теплоемкости (индекс адиабаты), в то время как давление и плотность обратно пропорциональны температуре и молекулярной массе, что делает только полностью независимые свойства температура и молекулярная структура важно (коэффициент теплоемкости может определяться температурой и молекулярной структурой, но простой молекулярной массы недостаточно для его определения).

Звук распространяется быстрее в низком молекулярный вес газы, такие как гелий чем в более тяжелых газах, таких как ксенон. Для одноатомных газов скорость звука составляет около 75% от средней скорости движения атомов в этом газе.

Для данного идеальный газ молекулярный состав фиксирован, и поэтому скорость звука зависит только от его температура. При постоянной температуре газ давление не влияет на скорость звука, так как плотность увеличивается, а давление и плотность (также пропорциональные давлению) имеют равное, но противоположное влияние на скорость звука, и два вклада точно компенсируются. Аналогичным образом волны сжатия в твердых телах зависят как от сжимаемости, так и от плотности - как и в жидкостях, - но в газах плотность способствует сжимаемости таким образом, что некоторая часть каждого атрибута учитывается, оставляя только зависимость от температуры, молекулярный вес и коэффициент теплоемкости, которые могут быть независимо получены из температуры и молекулярного состава (см. выводы ниже). Таким образом, для одного данного газа (при условии, что молекулярная масса не изменяется) и в небольшом диапазоне температур (для которого теплоемкость относительно постоянна) скорость звука становится зависимой только от температуры газа.

В режиме неидеального газа, для которого газ Ван дер Ваальса уравнение будет использоваться, пропорциональность не точна, и есть небольшая зависимость скорости звука от давления газа.

Влажность оказывает небольшое, но измеримое влияние на скорость звука (вызывая ее увеличение примерно на 0,1–0,6%), потому что кислород и азот молекулы воздуха заменяются более легкими молекулами воды. Это простой эффект смешивания.

Изменение высоты и последствия для атмосферной акустики

Плотность и давление плавно уменьшаются с высотой, а температура (красный цвет) - нет. Скорость звука (синий цвет) зависит только от сложного изменения температуры на высоте и может быть рассчитана на ее основе, поскольку отдельные эффекты плотности и давления на скорость звука взаимно компенсируют друг друга. Скорость звука увеличивается с высотой в двух областях стратосферы и термосферы из-за тепловых эффектов в этих областях.

в Атмосфера Земли, основным фактором, влияющим на скорость звука, является температура. Для данного идеального газа с постоянной теплоемкостью и составом скорость звука зависит от исключительно по температуре; видеть Подробности ниже. В таком идеальном случае эффекты пониженной плотности и пониженного давления на высоте компенсируют друг друга, за исключением остаточного эффекта температуры.

Поскольку температура (и, следовательно, скорость звука) уменьшается с увеличением высоты до 11 км, звук преломленный вверх, вдали от слушателей на земле, создавая акустическая тень на некотором удалении от источника.^[8] Уменьшение скорости звука с высотой называется отрицательным градиент скорости звука.

Однако есть вариации в этой тенденции выше. 11 км. В частности, в стратосфера выше о 20 кмскорость звука увеличивается с высотой из-за повышения температуры из-за нагрева внутри озоновый слой. Это дает положительный градиент скорости звука в этой области. Еще одна область положительного градиента наблюдается на очень больших высотах, в хорошо названном термосфера над 90 км.

Практическая формула для сухого воздуха

Приблизительное значение скорости звука в сухом воздухе на основе коэффициент теплоемкости (зеленым) на фоне усеченного Расширение Тейлора (в красном).

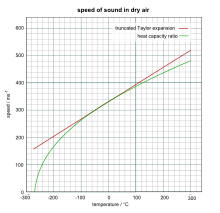
Приблизительная скорость звука в сухом (влажность 0%) воздухе в метрах в секунду при температуре около 0 ° C, можно рассчитать из

${ displaystyle c _ { mathrm {air}} = (331,3 + 0,606 cdot vartheta) ~~~ mathrm {m / s},}$

куда ${ displaystyle vartheta}$ это температура в градусах Цельсия (° С).^[9]

Это уравнение выводится из первых двух членов Расширение Тейлора следующего более точного уравнения:

${ displaystyle c _ { mathrm {air}} = 331.3 ~ { sqrt {1 + { frac { vartheta} {273.15}}}} ~~~~ mathrm {m / s}.}$

Разделив первую часть и умножив вторую часть с правой стороны, на √273.15 дает точно эквивалентную форму

${ displaystyle c _ { mathrm {air}} = 20.05 ~ { sqrt { vartheta +273.15}} ~~~~ mathrm {m / s}.}$

который также можно записать как

${ displaystyle c _ { mathrm {air}} = 20,05 ~ { sqrt {T}} ~~~~ mathrm {m / s}}$

куда Т обозначает термодинамическая температура.

Значение 331,3 м / с, который представляет собой скорость на 0 ° C (или же 273,15 К), основан на теоретических (и некоторых измеренных) значениях коэффициент теплоемкости, γ, а также о том, что при 1 банкомат реальный воздух очень хорошо описывается приближением идеального газа. Обычно встречающиеся значения скорости звука при 0 ° C может варьироваться от 331,2 до 331,6 из-за допущений, сделанных при его расчете. Если идеальный газ γ предполагается 7/5 = 1.4 точно, 0 ° C скорость рассчитывается (см. раздел ниже) как 331,3 м / с, коэффициент, использованный выше.

Это уравнение верно для гораздо более широкого диапазона температур, но все же зависит от приближения коэффициента теплоемкости, не зависящего от температуры, и по этой причине не будет работать, особенно при более высоких температурах. Он дает хорошие прогнозы в относительно сухих, холодных условиях с низким давлением, таких как земные стратосфера. Уравнение не работает при чрезвычайно низких давлениях и коротких длинах волн из-за зависимости от предположения, что длина волны звука в газе намного больше средней длины волны. длина свободного пробега между столкновениями молекул газа. Вывод этих уравнений будет дан в следующем разделе.

График, на котором сравниваются результаты двух уравнений, показан справа, с немного разным значением 331,5 м / с для скорости звука при 0 ° C.^[10]

Подробности

Скорость звука в идеальных газах и воздухе

Для идеального газа K (в объемный модуль в уравнениях выше, эквивалентных C, коэффициент жесткости в твердых телах) определяется как

${ Displaystyle К = гамма cdot p,}$

таким образом, из приведенного выше уравнения Ньютона – Лапласа скорость звука в идеальном газе определяется выражением

${ displaystyle c = { sqrt { gamma cdot {p over rho}}},}$

куда

• γ это индекс адиабаты также известный как коэффициент изоэнтропического расширения. Это отношение удельной теплоемкости газа при постоянном давлении к теплоемкости газа при постоянном объеме (${ Displaystyle C_ {p} / C_ {v}}$) и возникает потому, что классическая звуковая волна вызывает адиабатическое сжатие, при котором теплота сжатия не успевает покинуть импульс давления и, таким образом, способствует давлению, вызванному сжатием;
• п это давление;
• ρ это плотность.

С использованием идеальный газ закон заменить п с nRT/Vи заменив ρ с нМ/V, уравнение для идеального газа принимает вид

${ displaystyle c _ { mathrm {ideal}} = { sqrt { gamma cdot {p over rho}}} = { sqrt { gamma cdot R cdot T over M}} = { sqrt { gamma cdot k cdot T over m}},}$

куда

• c_{идеальный} скорость звука в идеальный газ;
• р (примерно 8.314463 Дж · К⁻¹· Моль⁻¹) это молярная газовая постоянная (универсальная газовая постоянная);^[11]
• k это Постоянная Больцмана;
• γ (гамма) это индекс адиабаты. При комнатной температуре, когда тепловая энергия полностью распределяется на вращение (вращения полностью возбуждаются), но квантовые эффекты предотвращают возбуждение колебательных мод, значение равно 7/5 = 1.400 для двухатомных молекул согласно кинетической теории. Гамма фактически измеряется экспериментально в диапазоне от 1,3991 до 1,403 при 0 ° C, для воздуха. Гамма точно 5/3 = 1.6667 для одноатомных газов, таких как благородные газы а для газов с трехатомными молекулами - приблизительно 1,3;
• Т абсолютная температура;
• M - молярная масса газа. Средняя молярная масса для сухого воздуха составляет около 0,028,964,5 кг / моль;^{[нужна цитата ]}
• п количество молей;
• м - масса отдельной молекулы.

Это уравнение применяется только тогда, когда звуковая волна представляет собой небольшое возмущение для условий окружающей среды, и выполняются некоторые другие отмеченные условия, как указано ниже. Расчетные значения для c_{воздуха} были обнаружены незначительные отклонения от экспериментально определенных значений.^[12]

Ньютон считался известной скоростью звука до появления большей части термодинамика и так неправильно использовали изотермический расчеты вместо адиабатический. В его результате отсутствовал фактор γ но в остальном был прав.

Численная замена приведенных выше значений дает приближение скорости звука для газов в идеальном газе, которое является точным при относительно низких давлениях и плотностях газа (для воздуха это включает стандартные условия на уровне Земли на уровне моря). Кроме того, для двухатомных газов использование γ = 1.4000 требует, чтобы газ существовал в достаточно высоком температурном диапазоне, чтобы вращательная теплоемкость была полностью возбуждена (т.е. вращение молекул полностью использовалось в качестве «перегородки» или резервуара тепловой энергии); но в то же время температура должна быть достаточно низкой, чтобы молекулярные колебательные моды не вносили вклад в теплоемкость (т. е. незначительное тепло переходит в вибрацию, поскольку все колебательные квантовые моды выше моды минимальной энергии имеют слишком высокие энергии, чтобы их мог заселить значительное количество молекул при этой температуре). Для воздуха эти условия выполняются при комнатной температуре, а также при температурах значительно ниже комнатной (см. Таблицы ниже). См. Раздел о газах в удельная теплоемкость для более полного обсуждения этого явления.

Для воздуха мы вводим сокращение

${ displaystyle R _ {*} = R / M _ { mathrm {air}}.}$

Кроме того, переключаемся на температуру по Цельсию ${ displaystyle vartheta}$ = Т − 273.15, что полезно для расчета скорости воздуха в районе 0 ° C (около 273 кельвина). Затем для сухого воздуха

${ displaystyle c _ { mathrm {air}} = { sqrt { gamma cdot R _ {*} cdot T}} = { sqrt { gamma cdot R _ {*} cdot ( vartheta +273,15) }},}$

${ displaystyle c _ { mathrm {air}} = { sqrt { gamma cdot R _ {*} cdot 273.15}} cdot { sqrt {1 + { frac { vartheta} {273.15}}}} ,}$

куда ${ displaystyle vartheta}$ (тета) - температура в градусах Цельсия (° С).

Подстановка числовых значений

${ Displaystyle R = 8,314 , 463 ~ mathrm {J / (моль cdot K)}}$

для моляра газовая постоянная в Дж / моль / Кельвин, и

${ displaystyle M _ { mathrm {air}} = 0,028 , 964 , 5 ~ mathrm {кг / моль}}$

для средней молярной массы воздуха в кг; и используя идеальное значение двухатомного газа γ = 1.4000, у нас есть

${ displaystyle c _ { mathrm {air}} = 331.3 ~~ { sqrt {1 + { frac { vartheta} {273.15}}}} ~~~ mathrm {m / s}.}$

Наконец, разложение Тейлора оставшегося квадратного корня в ${ displaystyle vartheta}$ дает

${ displaystyle c _ { mathrm {air}} = 331.3 ~ (1 + { frac { vartheta} {2 cdot 273.15}}) ~~~ mathrm {m / s},}$

${ displaystyle c _ { mathrm {air}} = (331,3 + 0,606 cdot vartheta) ~~~ mathrm {m / s}.}$

Приведенный выше вывод включает первые два уравнения, приведенные в разделе «Практическая формула для сухого воздуха» выше.

Воздействие сдвига ветра

Скорость звука зависит от температуры. Поскольку температура и скорость звука обычно уменьшаются с увеличением высоты, звук преломленный вверх, вдали от слушателей на земле, создавая акустическая тень на некотором удалении от источника.^[8] Сдвиг ветра 4 м / (с · км) может вызвать рефракцию, равную типичной температуре. скорость отклонения из 7,5 ° C / км.^[13] Более высокие значения градиента ветра будут преломлять звук вниз к поверхности по ветру,^[14] устранение акустической тени на подветренной стороне. Это повысит слышимость звуков с подветренной стороны. Этот эффект преломления по ветру возникает из-за градиента ветра; звук не уносится ветром.^[15]

Для распространения звука экспоненциальное изменение скорости ветра с высотой можно определить следующим образом:^[16]

${ Displaystyle U (час) = U (0) час ^ { zeta},}$

${ displaystyle { frac { mathrm {d} U} { mathrm {d} H}} (h) = zeta { frac {U (h)} {h}},}$

куда

• U(час) - скорость ветра на высоте час;
• ζ - экспоненциальный коэффициент, основанный на шероховатости поверхности земли, обычно от 0,08 до 0,52;
• dU/ дЧАС(час) - ожидаемый градиент ветра на высоте час.

В 1862 г. американская гражданская война Битва при Юке акустическая тень, которая, как считается, была усилена северо-восточным ветром, не позволила двум дивизиям солдат Союза попасть в бой,^[17] потому что они не могли слышать только звуки боя 10 км (шесть миль) по ветру.^[18]

Столы

в стандартная атмосфера:

• Т₀ является 273,15 К (= 0 ° C = 32 ° F), что дает теоретическое значение 331,3 м / с (= 1086.9 фут / с = 1193 км / ч = 741,1 миль / ч = 644.0 кн). Однако значения в диапазоне от 331,3 до 331,6 м / с можно найти в справочной литературе;
• Т₂₀ является 293,15 К (= 20 ° C = 68 ° F), что дает значение 343,2 м / с (= 1126.0 фут / с = 1236 км / ч = 767,8 миль / ч = 667.2 кн);
• Т₂₅ является 298,15 К (= 25 ° C = 77 ° F), что дает значение 346,1 м / с (= 1135,6 фут / с = 1246 км / ч = 774,3 миль / ч = 672.8 кн).

Фактически, если предположить идеальный газ, скорость звука c зависит только от температуры, не под давлением или же плотность (поскольку они изменяются синхронно для данной температуры и отменяются). Воздух - почти идеальный газ. Температура воздуха меняется с высотой, что дает следующие изменения скорости звука при использовании стандартной атмосферы:фактические условия могут отличаться.

При нормальных атмосферных условиях температура и, следовательно, скорость звука зависят от высоты:

Влияние частоты и состава газа

Общие физические соображения

Среда, в которой распространяется звуковая волна, не всегда реагирует адиабатически, и в результате скорость звука может изменяться с частотой.^[19]

Ограничения концепции скорости звука из-за чрезмерного затухания также вызывают озабоченность. Затухание, которое существует на уровне моря для высоких частот, применяется к последовательно более низким частотам по мере снижения атмосферного давления или длина свободного пробега увеличивается. По этой причине концепция скорости звука (за исключением частот, приближающихся к нулю) постепенно теряет свой диапазон применимости на больших высотах.^[12] Стандартные уравнения скорости звука применимы с разумной точностью только к ситуациям, когда длина звуковой волны значительно больше, чем длина свободного пробега молекул в газе.

Молекулярный состав газа влияет как на массу (M) молекул, так и на их теплоемкость, и поэтому оба фактора влияют на скорость звука. Как правило, при той же молекулярной массе одноатомные газы имеют немного более высокую скорость звука (более чем на 9%), потому что они имеют более высокую скорость звука. γ (5/3 = 1.66...) чем диатомовые (7/5 = 1.4). Таким образом, при той же молекулярной массе скорость звука одноатомного газа увеличивается в несколько раз.

${ displaystyle {c _ { mathrm {gas, monatomic}} over c _ { mathrm {gas, diatomic}}} = { sqrt {{5/3} over {7/5}}} = { sqrt {25 более 21}} = 1,091 ldots}$

Это дает разницу в 9%, что является типичным соотношением скорости звука при комнатной температуре в гелий против. дейтерий, каждый с молекулярной массой 4. Звук в гелии распространяется быстрее, чем в дейтерии, потому что адиабатическое сжатие нагревает гелий больше, поскольку молекулы гелия могут накапливать тепловую энергию от сжатия только при поступательном движении, но не при вращении. Таким образом, молекулы гелия (одноатомные молекулы) быстрее перемещаются в звуковой волне и быстрее передают звук. (Звук распространяется со скоростью примерно 70% от средней молекулярной скорости в газах; этот показатель составляет 75% в одноатомных газах и 68% в двухатомных газах).

Обратите внимание, что в этом примере мы предположили, что температура достаточно низкая, чтобы на теплоемкость не влияла молекулярная вибрация (см. теплоемкость ). Однако колебательные моды просто вызывают гаммы, которые уменьшаются до 1, поскольку колебательные моды в многоатомном газе дают газу дополнительные способы хранения тепла, которые не влияют на температуру и, таким образом, не влияют на скорость молекул и скорость звука. Таким образом, влияние более высоких температур и колебательной теплоемкости увеличивает разницу между скоростью звука в одноатомных и многоатомных молекулах, при этом скорость остается большей в одноатомных.

Практическое применение в воздухе

Безусловно, наиболее важным фактором, влияющим на скорость звука в воздухе, является температура. Скорость пропорциональна квадратному корню из абсолютной температуры, что дает увеличение примерно на 0,6 м / с на градус Цельсия. По этой причине высота звука музыкального духового инструмента увеличивается с увеличением его температуры.

Скорость звука увеличивается из-за влажности, но уменьшается из-за углекислого газа. Разница между влажностью 0% и 100% составляет около 1,5 м / с при стандартных давлении и температуре, но величина эффекта влажности резко возрастает с увеличением температуры. Содержание углекислого газа в воздухе не является фиксированным из-за как загрязнения углерода, так и дыхания человека (например, в воздухе, продуваемом ветровыми инструментами).

Зависимость от частоты и давления в практических приложениях обычно незначительна. В сухом воздухе скорость звука увеличивается примерно на 0,1 м / с по мере увеличения частоты от 10 Гц к 100 Гц. Для слышимых частот выше 100 Гц он относительно постоянен. Стандартные значения скорости звука указаны в пределе низких частот, где длина волны больше по сравнению со средней длиной свободного пробега.^[20]

Как показано выше, приблизительное значение 1000/3 = 333,33 ... м / с является точным немного ниже 5 ° C и является хорошим приближением для всех «обычных» наружных температур (по крайней мере, в умеренном климате), отсюда и обычные эмпирическое правило, чтобы определить, как далеко ударила молния: посчитайте секунды от начала вспышки молнии до начала соответствующего раската грома и разделите на 3: результат - расстояние в километрах до ближайшей точки удара молнии .

число Маха

ВМС США F / A-18 путешествует со скоростью, близкой к скорости звука. Белый ореол состоит из капель конденсированной воды, образовавшейся в результате резкого падения давления воздуха за ударным конусом вокруг самолета (см. Сингулярность Прандтля-Глауэрта ).^[21]

Число Маха, полезная величина в аэродинамике, представляет собой отношение воздуха скорость к местной скорости звука. На высоте, по объясненным причинам, число Маха зависит от температуры. летные инструменты однако для вычисления числа Маха используйте перепад давления, а не температуру. Предполагается, что конкретное давление представляет собой конкретную высоту и, следовательно, стандартную температуру. Летные приборы самолета должны работать таким образом, потому что давление застоя, ощущаемое Трубка Пито зависит как от высоты, так и от скорости.

Экспериментальные методы

Существует ряд различных методов измерения звука в воздухе.

Самая ранняя достаточно точная оценка скорости звука в воздухе была сделана Уильям Дерхам и признан Исаак Ньютон. У Дерхама был телескоп на вершине башни Церковь Святого Лаврентия в Upminster, Англия. В безветренный день синхронизированные карманные часы давали помощнику, который стрелял из дробовика в заранее определенное время с заметной точки за несколько миль от дома, через сельскую местность. Это может быть подтверждено телескопом. Затем он измерил интервал между появлением дыма и появлением звука с помощью полусекундного маятника. Расстояние от места выстрела определялось триангуляцией, и простое деление (расстояние / время) давало скорость. Наконец, проведя множество наблюдений с использованием диапазона различных расстояний, можно усреднить неточность полусекундного маятника, дав ему окончательную оценку скорости звука. Современные секундомеры позволяют использовать этот метод сегодня на дистанциях от 200 до 400 метров, и при этом не требуется что-то более громкое, чем дробовик.

Методы однократного отсчета времени

Самая простая концепция - это измерение с использованием двух микрофоны и быстрое записывающее устройство, такое как цифровой объем хранения. В этом методе используется следующая идея.

Если источник звука и два микрофона расположены по прямой линии с источником звука на одном конце, то можно измерить следующее:

1. Расстояние между микрофонами (Икс), называемая микрофонной основой.
2. Время прибытия между сигналами (задержка), достигающими разных микрофонов (т).

потом v = Икс/т.

Другие методы

В этих методах время измерение было заменено измерением, обратным времени (частота ).

Трубка Кундта это пример эксперимента, который можно использовать для измерения скорости звука в небольшом объеме. Его преимущество в том, что он может измерять скорость звука в любом газе. Этот метод использует порошок, чтобы сделать узлы и пучности видны человеческому глазу. Это пример компактной экспериментальной установки.

А камертон можно держать возле устья длинного трубка который окунается в бочку с воды. In this system it is the case that the pipe can be brought to resonance if the length of the air column in the pipe is equal to (1 + 2п)λ/4 куда п целое число. Поскольку antinodal point for the pipe at the open end is slightly outside the mouth of the pipe it is best to find two or more points of resonance and then measure half a wavelength between these.

Here it is the case that v = fλ.

High-precision measurements in air

The effect of impurities can be significant when making high-precision measurements. Химическая осушители can be used to dry the air, but will, in turn, contaminate the sample. The air can be dried cryogenically, but this has the effect of removing the carbon dioxide as well; therefore many high-precision measurements are performed with air free of carbon dioxide rather than with natural air. A 2002 review^[22] found that a 1963 measurement by Smith and Harlow using a cylindrical resonator gave "the most probable value of the standard speed of sound to date." The experiment was done with air from which the carbon dioxide had been removed, but the result was then corrected for this effect so as to be applicable to real air. The experiments were done at 30 ° С but corrected for temperature in order to report them at 0 ° C. Результат был 331.45 ± 0.01 m/s for dry air at STP, for frequencies from 93 Hz к 1,500 Hz.

Non-gaseous media

Speed of sound in solids

Three-dimensional solids

In a solid, there is a non-zero stiffness both for volumetric deformations and shear deformations. Hence, it is possible to generate sound waves with different velocities dependenton the deformation mode. Sound waves generating volumetric deformations (compression) and shear deformations (shearing) are called pressure waves (longitudinal waves) and shear waves (transverse waves), respectively. В землетрясения, the corresponding seismic waves are called P-waves (primary waves) and S-волны (secondary waves), respectively. The sound velocities of these two types of waves propagating in a homogeneous 3-dimensional solid are respectively given by^[23]

${displaystyle c_{mathrm {solid,p} }={sqrt {frac {K+{frac {4}{3}}G}{ ho }}}={sqrt {frac {E(1- u )}{ ho (1+ u )(1-2 u )}}},}$

${displaystyle c_{mathrm {solid,s} }={sqrt {frac {G}{ ho }}},}$

куда

• K это объемный модуль of the elastic materials;
• грамм это модуль сдвига of the elastic materials;
• E это Модуль для младших;
• ρ is the density;
• ν является Коэффициент Пуассона.

The last quantity is not an independent one, as E = 3K(1 − 2ν). Note that the speed of pressure waves depends both on the pressure and shear resistance properties of the material, while the speed of shear waves depends on the shear properties only.

Typically, pressure waves travel faster in materials than do shear waves, and in earthquakes this is the reason that the onset of an earthquake is often preceded by a quick upward-downward shock, before arrival of waves that produce a side-to-side motion. For example, for a typical steel alloy, K = 170 GPa, грамм = 80 GPa и ρ = 7,700 kg/m³, yielding a compressional speed c_solid,p из 6,000 m/s.^[23] This is in reasonable agreement with c_solid,p measured experimentally at 5,930 m/s for a (possibly different) type of steel.^[24] The shear speed c_solid,s is estimated at 3,200 m/s using the same numbers.

One-dimensional solids

The speed of sound for pressure waves in stiff materials such as metals is sometimes given for "long rods" of the material in question, in which the speed is easier to measure. In rods where their diameter is shorter than a wavelength, the speed of pure pressure waves may be simplified and is given by:^[25]

${displaystyle c_{mathrm {solid} }={sqrt {frac {E}{ ho }}},}$

куда E является Модуль для младших. This is similar to the expression for shear waves, save that Модуль для младших заменяет модуль сдвига. This speed of sound for pressure waves in long rods will always be slightly less than the same speed in homogeneous 3-dimensional solids, and the ratio of the speeds in the two different types of objects depends on Коэффициент Пуассона for the material.

Speed of sound in liquids

Speed of sound in water vs temperature.

In a fluid, the only non-zero жесткость is to volumetric deformation (a fluid does not sustain shear forces).

Hence the speed of sound in a fluid is given by

${displaystyle c_{mathrm {fluid} }={sqrt {frac {K}{ ho }}},}$

куда K это объемный модуль жидкости.

Вода

In fresh water, sound travels at about 1481 m/s в 20 ° C (see the External Links section below for online calculators).^[26] Применение подводный звук можно найти в сонар, акустическая коммуникация и акустическая океанография.

Морская вода

Speed of sound as a function of depth at a position north of Hawaii in the Тихий океан derived from the 2005 Атлас Мирового океана. В ГНФАР канал spans the minimum in the speed of sound at about 750-m depth.

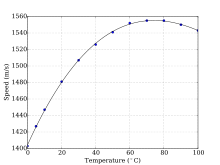
In salt water that is free of air bubbles or suspended sediment, sound travels at about 1500 m/s (1500.235 m/s в 1000 килопаскали, 10 °C and 3% соленость by one method).^[27] The speed of sound in seawater depends on pressure (hence depth), temperature (a change of 1 ° C ~ 4 м / с), и соленость (a change of 1‰ ~ 1 м / с), and empirical equations have been derived to accurately calculate the speed of sound from these variables.^[28][29] Other factors affecting the speed of sound are minor. Since in most ocean regions temperature decreases with depth, the profile of the speed of sound with depth decreases to a minimum at a depth of several hundred metres. Below the minimum, sound speed increases again, as the effect of increasing pressure overcomes the effect of decreasing temperature (right).^[30] For more information see Dushaw et al.^[31]

An empirical equation for the speed of sound in sea water is provided by Mackenzie:^[32]

${displaystyle c(T,S,z)=a_{1}+a_{2}T+a_{3}T^{2}+a_{4}T^{3}+a_{5}(S-35)+a_{6}z+a_{7}z^{2}+a_{8}T(S-35)+a_{9}Tz^{3},}$

куда

• Т is the temperature in degrees Celsius;
• S is the salinity in parts per thousand;
• z is the depth in metres.

Константы а₁, а₂, ..., а₉ находятся

${displaystyle {egin{aligned}a_{1}&=1,448.96,&a_{2}&=4.591,&a_{3}&=-5.304 imes 10^{-2},a_{4}&=2.374 imes 10^{-4},&a_{5}&=1.340,&a_{6}&=1.630 imes 10^{-2},a_{7}&=1.675 imes 10^{-7},&a_{8}&=-1.025 imes 10^{-2},&a_{9}&=-7.139 imes 10^{-13},end{aligned}}}$

with check value 1550.744 m/s за Т = 25 °C, S = 35 parts per thousand, z = 1,000 m. This equation has a standard error of 0.070 m/s for salinity between 25 and 40 ppt. Видеть Technical Guides. Speed of Sound in Sea-Water for an online calculator.

(Note: The Sound Speed vs. Depth graph does нет correlate directly to the MacKenzie formula.This is due to the fact that the temperature and salinity varies at different depths.When Т и S are held constant, the formula itself is always increasing with depth.)

Other equations for the speed of sound in sea water are accurate over a wide range of conditions, but are far more complicated, e.g., that by V. A. Del Grosso^[33] and the Chen-Millero-Li Equation.^[31][34]

Speed of sound in plasma

The speed of sound in a плазма for the common case that the electrons are hotter than the ions (but not too much hotter) is given by the formula (see здесь )

${displaystyle c_{s}=(gamma ZkT_{mathrm {e} }/m_{mathrm {i} })^{1/2}=90.85(gamma ZT_{e}/mu )^{1/2}~mathrm {m/s} ,}$

куда

• м_я это ион mass;
• μ is the ratio of ion mass to протон масса μ = м_я/м_п;
• Т_е это электрон temperature;
• Z is the charge state;
• k является Постоянная Больцмана;
• γ это индекс адиабаты.

In contrast to a gas, the pressure and the density are provided by separate species, the pressure by the electrons and the density by the ions. The two are coupled through a fluctuating electric field.

Градиенты

When sound spreads out evenly in all directions in three dimensions, the intensity drops in proportion to the inverse square of the distance. However, in the ocean, there is a layer called the 'deep sound channel' or ГНФАР канал which can confine sound waves at a particular depth.

In the SOFAR channel, the speed of sound is lower than that in the layers above and below. Just as light waves will refract towards a region of higher индекс, sound waves will преломлять towards a region where their speed is reduced. The result is that sound gets confined in the layer, much the way light can be confined to a sheet of glass or оптоволокно. Thus, the sound is confined in essentially two dimensions. In two dimensions the intensity drops in proportion to only the inverse of the distance. This allows waves to travel much further before being undetectably faint.

A similar effect occurs in the atmosphere. Проект Могул successfully used this effect to detect a ядерный взрыв at a considerable distance.

Смотрите также

• Акустоупругий эффект
• Упругая волна
• Второй звук
• ударная волна
• Звуковой барьер
• Speeds of sound of the elements
• Подводная акустика
• Вибрации

Рекомендации

внешняя ссылка

• Speed of Sound Calculator
• Calculation: Speed of Sound in Air and the Temperature
• Speed of sound: Temperature Matters, Not Air Pressure
• Properties of the U.S. Standard Atmosphere 1976
• Скорость звука
• How to Measure the Speed of Sound in a Laboratory
• Did Sound Once Travel at Light Speed?
• Acoustic Properties of Various Materials Including the Speed of Sound
• Discovery of Sound in the Sea (uses of sound by humans and other animals)