Интервал Пифагора - Википедия - Pythagorean interval
 | В ведущий раздел этой статьи может потребоваться переписать. (Ноябрь 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
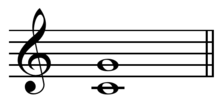
Играть в (помощь ·Информация ): C-G (3/2 ÷ 1/1 = 3/2).В музыкальный тюнинг теория, Пифагоров интервал это музыкальный интервал с соотношение частот равно мощность два, разделенные на степень трех, или наоборот.[1] Например, идеальный пятый с соотношением 3/2 (эквивалент 31/21) и идеальный четвертый с соотношением 4/3 (эквивалент 22/31) - пифагоровы интервалы.
Все интервалы между нотами гаммы являются пифагорейскими, если они настроены с помощью Пифагорейский тюнинг система. Однако некоторые интервалы Пифагора также используются в других системах настройки. Например, упомянутые выше пифагоровы совершенные пятая и четвертая части также используются в просто интонация.
Таблица интервалов
| Имя | короткий | Другие имена) | Соотношение | Факторы | Вывод | Центов | ET Центов | MIDI файл | Пятые |
|---|---|---|---|---|---|---|---|---|---|
| уменьшился второй | d2 | 524288/531441 | 219/312 | -23.460 | 0 | играть в (помощь ·Информация ) | -12 | ||
| (идеально) унисон | P1 | 1/1 | 30/20 | 1/1 | 0.000 | 0 | играть в (помощь ·Информация ) | 0 | |
| Пифагорейская запятая | 531441/524288 | 312/219 | 23.460 | 0 | играть в (помощь ·Информация ) | 12 | |||
| второстепенная секунда | m2 | Лимма, диатонический полутон, минорный полутон | 256/243 | 28/35 | 90.225 | 100 | играть в (помощь ·Информация ) | -5 | |
| усиленный унисон | A1 | апотом, хроматический полутон, мажорный полутон | 2187/2048 | 37/211 | 113.685 | 100 | играть в (помощь ·Информация ) | 7 | |
| уменьшенная треть | d3 | тон весь тон, весь шаг | 65536/59049 | 216/310 | 180.450 | 200 | играть в (помощь ·Информация ) | -10 | |
| основная секунда | M2 | 9/8 | 32/23 | 3·3/2·2 | 203.910 | 200 | играть в (помощь ·Информация ) | 2 | |
| полудитон | м3 | (Пифагорейский второстепенная треть ) | 32/27 | 25/33 | 294.135 | 300 | играть в (помощь ·Информация ) | -3 | |
| увеличенная секунда | A2 | 19683/16384 | 39/214 | 317.595 | 300 | играть в (помощь ·Информация ) | 9 | ||
| уменьшился четвертый | d4 | 8192/6561 | 213/38 | 384.360 | 400 | играть в (помощь ·Информация ) | -8 | ||
| ditone | M3 | (Пифагорейский большая треть ) | 81/64 | 34/26 | 27·3/32·2 | 407.820 | 400 | играть в (помощь ·Информация ) | 4 |
| идеальный четвертый | P4 | диатессарон сесквитерций | 4/3 | 22/3 | 2·2/3 | 498.045 | 500 | играть в (помощь ·Информация ) | -1 |
| дополненная треть | A3 | 177147/131072 | 311/217 | 521.505 | 500 | играть в (помощь ·Информация ) | 11 | ||
| уменьшенная пятая | d5 | тритон | 1024/729 | 210/36 | 588.270 | 600 | играть в (помощь ·Информация ) | -6 | |
| дополненный четвертый | A4 | 729/512 | 36/29 | 611.730 | 600 | играть в (помощь ·Информация ) | 6 | ||
| уменьшился шестой | d6 | 262144/177147 | 218/311 | 678.495 | 700 | играть в (помощь ·Информация ) | -11 | ||
| идеальный пятый | P5 | диапенте, полуторный | 3/2 | 31/21 | 3/2 | 701.955 | 700 | играть в (помощь ·Информация ) | 1 |
| второстепенный шестой | m6 | 128/81 | 27/34 | 792.180 | 800 | играть в (помощь ·Информация ) | -4 | ||
| расширенная пятая | A5 | 6561/4096 | 38/212 | 815.640 | 800 | играть в (помощь ·Информация ) | 8 | ||
| уменьшился седьмой | d7 | 32768/19683 | 215/39 | 882.405 | 900 | играть в (помощь ·Информация ) | -9 | ||
| основной шестой | M6 | 27/16 | 33/24 | 9·3/8·2 | 905.865 | 900 | играть в (помощь ·Информация ) | 3 | |
| второстепенный седьмой | m7 | 16/9 | 24/32 | 996.090 | 1000 | играть в (помощь ·Информация ) | -2 | ||
| дополненный шестой | A6 | 59049/32768 | 310/215 | 1019.550 | 1000 | играть в (помощь ·Информация ) | 10 | ||
| уменьшенная октава | d8 | 4096/2187 | 212/37 | 1086.315 | 1100 | играть в (помощь ·Информация ) | -7 | ||
| основной седьмой | M7 | 243/128 | 35/27 | 81·3/64·2 | 1109.775 | 1100 | играть в (помощь ·Информация ) | 5 | |
| уменьшенная девятая | d9 | (октава - запятая) | 1048576/531441 | 220/312 | 1176.540 | 1200 | играть в (помощь ·Информация ) | -12 | |
| (идеально) октава | P8 | диапазон | 2/1 | 2/1 | 1200.000 | 1200 | играть в (помощь ·Информация ) | 0 | |
| расширенный седьмой | A7 | (октава + запятая) | 531441/262144 | 312/218 | 1223.460 | 1200 | играть в (помощь ·Информация ) | 12 |
Обратите внимание, что условия ditone и полудитон специфичны для пифагорейской настройки, а тон и тритон используются в основном для всех систем настройки. Несмотря на свое название, полудитон (3 полутона, или около 300 центов) вряд ли можно рассматривать как половину дитона (4 полутона, или около 400 центов).
12-тональная шкала Пифагора
В таблице показано, из каких нот некоторые из вышеперечисленных интервалов можно играть на инструменте с использованием 12-тональной шкалы с повторяющимися октавами (например, фортепиано), настроенной с помощью симметричной пифагорейской настройки на основе D. Более подробную информацию об этой таблице можно найти в Размер пифагоровых интервалов.
Играть в (помощь ·Информация ): D-A + (27/16 ÷ 9/8 = 3/2).
Играть в (помощь ·Информация ), одна идеальная квинта перевернута (4/3 ÷ 1/1 = 4/3).
Играть в (помощь ·Информация ): C-D (9/8 ÷ 3/2 = 3/2), две идеальных пифагорейских пятых.
Играть в (помощь ·Информация ), две идеальные пятые перевернуты.
Играть в (помощь ·Информация ), три пифагорейских идеальных пятых.
Играть в (помощь ·Информация ), три пифагорейских идеальных пятых перевернуты.
Играть в (помощь ·Информация ), четыре пифагорейских идеальных пятых.
Играть в (помощь ·Информация ), четыре пифагорейских идеальных пятых перевернуты.
Играть в (помощь ·Информация ), пять пифагорейских идеальных пятых.
Играть в (помощь ·Информация ), шесть пифагорейских идеальных пятых.
Играть в (помощь ·Информация ), шесть пифагорейских идеальных пятых перевернутых.Фундаментальные интервалы
Основные интервалы - это сверхчастичные отношения 2/1, 3/2 и 4/3. 2/1 - это октава или же диапазон (Греческий для "по всему"). 3/2 - это идеальный пятый, диапент («через пять») или полуторный. 4/3 - это идеальный четвертый, диатессарон («через четыре») или сесквитерций. Эти три интервала и их октавные эквиваленты, такие как совершенные одиннадцатый и двенадцатый, являются единственными абсолютными созвучия системы Пифагора. Все остальные интервалы имеют разную степень диссонанса, от плавного до грубого.
Разница между идеальной четвертой и идеальной пятой - это тон или же основная секунда. Это соотношение 9/8, также известное как эпогдун и это единственное другое сверхчастичное соотношение пифагорейской настройки, как показано Теорема Стёрмера.
Два тона создают ditoneдиссонирующе широкий большая треть, соотношение 81/64. Дитон отличается от только мажорной трети (5/4) тем, что синтоническая запятая (81/80). Точно так же разница между тоном и идеальной четвертой - это полудитон, Стрелка второстепенная треть, 32/27, который отличается от 6/5 синтонической запятой. Эти различия «смягчаются» или устраняются путем компромиссов в имел в виду один темперамент.
Разница между второстепенной третью и тоном заключается в минорный полутон или же Лимма из 256/243. Разница между тоном и лиммой заключается в мажорный полутон или же апотом ("часть отрезана") от 2187/2048. Хотя лимма и апотом представлены одним шагом из 12 шагов равный темперамент, они не равны в настройке Пифагора, и их различие, 531441/524288, известно как Пифагорейская запятая.
Контраст с современной номенклатурой
Между названиями интервалов (количество шагов шкалы + качество) и частотными соотношениями существует взаимно однозначное соответствие. Это контрастирует с одинаковым темпераментом, в котором интервалы с одинаковым соотношением частот могут иметь разные названия (например, уменьшенная квинта и увеличенная четвертая); и с другими формами интонации, в которых интервалы с одинаковым названием могут иметь разные соотношения частот (например, 9/8 для большой секунды от C до D, но 10/9 для большой секунды от D до E).
Играть в (помощь ·Информация ).Смотрите также
- Созданная коллекция
- Просто интонация
- Список подразумеваемых интервалов
- Список интервалов в 5-предельной интонации
- Shí-èr-lǜ
- Целостная шкала
Источники
- ^ Бенсон, Дональд С. (2003). Более гладкий камешек: математические исследования, стр.56. ISBN 978-0-19-514436-9. «Частотное отношение каждого пифагорейского интервала - это соотношение между степенью двойки и степенью тройки ... подтверждая пифагорейские требования, чтобы все интервалы были связаны с отношениями целых чисел».
.PNG){kind=link}
