Вертолетный куб - Helicopter Cube
Тема этой статьи может не соответствовать Википедии рекомендации по продуктам и услугам. (Август 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В Вертолетный куб это Кубик Рубика -подобная головоломка, изобретенная Адамом Г. Коуэном в 2005 году и построенная в 2006 году.[1][2][3][4][5][6][7] Он также имеет форму куб. На первый взгляд, вертолетный куб может показаться комбинацией 2x2x2 и Skewb, но на самом деле он режет иначе и скручивает края куба, а не грани куба. Цель головоломки - перемешать цвета, а затем вернуть их в исходное состояние одного цвета для каждой грани.
Описание

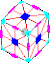
Куб вертолета выполнен в форме куба, разрезанного на 8 угловых частей и 24 грани в центре. Каждый угловой элемент имеет 3 цвета, а каждый центральный элемент лицевой стороны имеет только один цвет. В отличие от кубика Рубика, его грани не вращаются; скорее, части перемешиваются, вращаясь вокруг края куба.
При повороте головоломки поворот на 180 ° меняет местами две угловые части и меняет местами две пары центральных частей лица, но сохраняет форму куба. Таким образом можно разгадать всю головоломку.
Однако также можно повернуть край на ~ 71 °, так что основание двух групп угловой детали и центральной детали лицевой стороны каждая выровнено с плоскостью вращения другой кромки. Затем второй край можно повернуть, таким образом смешивая угловые части и центральные части лица и оставляя головоломку в некубической форме. Такое смешение известно как неуклюжий ход. Из-за различных форм смешанных частей, некоторые повороты, возможные в кубической форме, больше не могут быть возможны в перемешанной форме. Используя комбинацию таких «скачущих» движений, можно вернуться к кубической форме, но с некоторыми центральными частями лицевой стороны в неправильной ориентации, таким образом, выступающими наружу, как шипы, а не лежащими на поверхности куба. Также могут быть внесены более тонкие изменения, которые будут описаны позже.
Есть четыре варианта куба вертолета:
- оригинальный вертолетный куб, произведенный Twisty Store (продается также Уве Мефферт ), состоящий только из 8 угловых частей и 24 торцевых центральных частей;
- "Curvy Copter" Тома ван дер Зандена,[4] который имеет дополнительные 12 кромочных элементов по 2 цвета каждая. Это требует, чтобы человек строил вокруг краев, тогда как на кубе вертолета они спрятаны под ним, и не имеет значения, где вы строите.
- «Curvy Copter Plus», также созданный Томом ван дер Занденом, с дополнительными вырезами в середине центральных частей лица, что позволяет головоломке еще больше перемешиваться;
- "Helicopter Skewb", также созданный Томом Ван Дер Занденом, который выглядит точно так же, как и оригинальный Helicopter Cube, но также может вращаться, как и Skewb.
- «Пышный коптер 3», 2014 года выпуска на МФ8
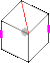
 Поворот на ~ 71 ° при подготовке к прыжку
Поворот на ~ 71 ° при подготовке к прыжку Начало беспорядочного движения
Начало беспорядочного движения Тщательно перемешанный куб вертолета
Тщательно перемешанный куб вертолета
Решения

Если головоломка решается только поворотом на 180 °, то очевидно, что ее можно решить, используя только поворот на 180 °. Однако, если были сделаны какие-то прыжки, даже если головоломка впоследствии была возвращена к форме куба, возможно, будет невозможно решить ее, используя только поворот на 180 °. Причина этого в том, что при повороте только на 180 ° каждая центральная часть лицевой стороны может быть переставлена только в рамках цикла из 6 элементов, часто называемого его орбита.[6] Центральные части лица на разных орбитах нельзя менять местами, используя только поворот на 180 °. Тем не менее, неуклюжие движения могут переставлять центральные части лица между разными орбитами, таким образом оставляя головоломку в состоянии, которое невозможно решить одним поворотом на 180 °.
Количество комбинаций
Предположим, что вертолетный куб скремблирован без скачкообразных движений (т.е. смешан только с поворотами на 180 градусов). Возможна любая перестановка углов, в том числе и нечетная. Семь углов можно независимо вращать, а ориентация восьмого зависит от остальных семи, давая 8! ×37 комбинации.
Есть 24 центра лица, которые можно расположить в 24! различные пути. Но центры лиц на самом деле расположены на 4 разных орбитах, каждая из которых содержит все цвета. Таким образом, количество перестановок сокращено до 6!4 распоряжения.[8] Перестановка центров граней четная, количество перестановок делится на 2.
Предполагая, что куб не имеет фиксированной ориентации в пространстве и что перестановки, возникающие в результате вращения куба без его скручивания, считаются идентичными, количество перестановок уменьшается в 24. Это происходит потому, что все 24 возможных положения и ориентации первый угол эквивалентен из-за отсутствия фиксированных центров. Этот фактор не появляется при вычислении перестановок кубов N × N × N, где N нечетно, так как эти головоломки имеют фиксированные центры, которые определяют пространственную ориентацию куба.
Это дает общее количество перестановок
Расширенное число 493694233804800000 (примерно 494 бильярда на длинная шкала или 494 квадриллиона в коротком масштабе).[6]
Когда вертолетный куб скремблируется движением, но все еще сохраняет свою форму куба, тогда центры граней не находятся на 4 разных орбитах. Если предположить, что четыре центра каждого цвета неразличимы, количество перестановок сокращается до 24! / (4!6) распоряжения. Уменьшающий коэффициент возникает из-за того, что существует 24 (4!) Способа расставить четыре части одного цвета. Это число возводится в шестую степень, потому что существует шесть цветов.
Это дает общее количество перестановок
Расширенное число 11928787020628077600000 (примерно 11929 триллион или 12 триллионов в длинной шкале или 12 секстиллионов в короткой шкале)[8]
Чтобы подсчитать позиции, не являющиеся кубами, нам нужно подсчитать все возможные формы (игнорируя цвета). Подсчитать эти фигуры сложно, поскольку иногда ходы блокируются исключительно из-за формы фигур, а не из-за основного механизма. Мэтт Галла провел полный анализ и изложил свои результаты в эта почта на форуме TwistyPuzzles. Я воспроизвел и проверил его результаты. Он нашел 14 098 форм, или 28 055, если считать и зеркальные изображения. Однако некоторые из них обладают симметрией и, следовательно, имеют менее 24 (или 48) возможных ориентаций. Вот разбивка этих симметрий:[8]
 |  |  |  |  |  |  |  |  |  |  |  | |||
| Сим. | Мистер4р3р2 | Мистер3р2 | р3р2 | мжр2e | мер2e | р2eр2e | м4 | ме | р2e | р2f | мc | я | Общий | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intl | Очас | D3D | D3 | C2v | C2ч | D2 | S4 | Cs | C2 | C2 | S2 | C1 | ||
| Schön. | м3м | 3м | 322 | мм2 | 2 / м | 222 | 4 | м | 2 | 2 | 1 | 1 | ||
| Заказ | 48 | 12 | 6 | 4 | 4 | 4 | 4 | 2 | 2 | 2 | 2 | 1 | ||
| Индекс | 1 | 4 | 8 | 12 | 12 | 12 | 12 | 24 | 24 | 24 | 24 | 48 | ||
| Формы зеркальное изображение | 1 | 1 | 8 | 1 | 18 | 4 | 1 | 82 | 764 | 5 | 37 | 13,176 | 14,098 | |
| 1 | 1 | 16 | 1 | 18 | 8 | 1 | 82 | 1,528 | 10 | 37 | 26,352 | 28,055 | ||
| Общий | 1 | 4 | 128 | 12 | 216 | 96 | 12 | 1,968 | 36,672 | 240 | 888 | 1,264,896 | 1,305,133 | |
В строке с пометкой Order показаны размеры групп симметрии. Индекс - это индекс группы симметрии как подгруппы полной кубической группы симметрии, то есть он равен 48, деленному на порядок. Индекс - это также количество способов, которыми любая конкретная форма с этой симметрией может быть ориентирована в пространстве (включая отражения). В первой строке «Фигуры» указано количество фигур, которые Мэтт нашел для каждой группы симметрии, но не считая зеркальных отображений, а вторая строка «Фигуры» включает в себя формы зеркальных отображений. Строка с пометкой "Итого" является произведением индекса и количества фигур.[8]
Умножение этого на предыдущий результат дает 15568653590593384802320800000 (примерно 15569 квадриллионов или 15 квадрильярдов в длинной шкале или 15 октиллионов в короткой шкале), позиции в целом запутались.[8]
Смотрите также
- Square One (головоломка), еще одна кубическая головоломка, меняющая форму.
Рекомендации
- ^ "Кубики вертолета Черное тело". Мефферта. Получено 2010-09-01.
Куб вертолета был задуман Адамом Г. Коуэном в 2005 году, но не был построен до 2006 года, когда Адам обнаружил, что 3D-печать может использоваться для изготовления деталей.
- ^ «Вертолетный куб - белое тело». Puzzle Master Inc. Архивировано из оригинал на 2011-07-06. Получено 2010-09-01.
- ^ Гетц Швандтнер. «Вертолет Куб белый». Чрезвычайно озадачивающий. Получено 2010-09-01.
Разработано: Adam Cowan
- ^ а б Том ван дер Занден. "Соблазнительный вертолет". Получено 2010-09-01.
Curvy Copter - моя самая популярная головоломка. Это вариант куба-вертолета Адама Г. Коуэна.
- ^ «Система извилистых головоломок». Архивировано из оригинал на 2010-08-07. Получено 2010-09-01.
Вертолетный куб был разработан и построен Адамом Г. Коуэном (Puzzlemaster42) и Кацухико Окамото (Кацухико) в 2007 году.
- ^ а б c "L'Helicopter Cube (французский)". fan2cube. Получено 2010-09-01.
- ^ Джейсон Смит. «Массовое производство вертолетного куба Адама Коуэна - 4/2010». Puzzle Forge. Получено 2010-09-01.
- ^ а б c d е Scherphuis, Jaap (12 декабря 2017 г.). «Вертолетный куб».






