N-мерная головоломка с последовательным ходом - N-dimensional sequential move puzzle

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «N-мерная головоломка с последовательным ходом»  – Новости  · газеты  · книги  · ученый  · JSTOR (Январь 2016) (Узнайте, как и когда удалить этот шаблон сообщения)

Пятимерный 2⁵ частичный разрез пазла, демонстрирующий, что даже при минимальном размере в 5-D головоломка далеко не тривиальна. На этом снимке экрана отчетливо видна четырехмерная природа наклеек.

В Кубик Рубика является оригинальным и наиболее известным трехмерным головоломки с последовательным ходом. Было много виртуальных реализаций этой головоломки в программного обеспечения. Это естественное расширение для создания головоломки с последовательным перемещением в более чем трех измерениях. Хотя физически такую ​​головоломку невозможно построить, правила ее действия довольно строго определены математически и аналогичны правилам трехмерной геометрии. Следовательно, их можно моделировать с помощью программного обеспечения. Как и в случае с головоломками с механическими последовательными движениями, есть рекорды для решателей, хотя еще и не такая же степень соревновательной организации.

Глоссарий

• Вершина. Точка нулевого измерения, в которой встречаются фигуры более высоких измерений.
• Край. Одномерная фигура, на которой встречаются фигуры более высоких измерений.
• Лицо. Двумерная фигура, на которой (для объектов размерностью больше трех) встречаются фигуры более высокой размерности.
• Клетка. Трехмерная фигура, на которой (для объектов размерностью больше четырех) встречаются фигуры более высокой размерности.
• п-Многогранник. А п-размерный рисунок продолжается, как указано выше. Определенная геометрическая фигура может заменить многогранник, где это уместно, например, 4-куб для обозначения тессеракт.
• п-клетка. Фигура более высокого измерения, содержащая п клетки.
• Кусок. Единственная подвижная часть головоломки, имеющая такую ​​же размерность, как и вся головоломка.
• Cubie. В сообществе решателей этот термин обычно используется для обозначения «кусочка».
• Наклейка. Цветные метки на головоломке, которые определяют состояние головоломки. Например, угловые кубики кубика Рубика представляют собой единое целое, но на каждом есть по три наклейки. Наклейки в головоломках с более высокой размерностью будут иметь размерность больше двух. Например, в 4-кубе наклейки представляют собой трехмерные твердые тела.

Для сравнения данные, относящиеся к стандарту 3³ Кубик Рубика выглядит следующим образом;

Количество возможных комбинаций${ displaystyle = { frac {12! cdot 8!} {2}} cdot { frac {2 ^ {12}} {2}} cdot { frac {3 ^ {8}} {3} } sim 10 ^ {20}}$

Есть некоторые споры о том, следует ли считать кубики с центром лица отдельными частями, поскольку они не могут перемещаться относительно друг друга. В разных источниках может быть разное количество произведений. В этой статье подсчитываются кубы с центром граней, поскольку это делает арифметические последовательности более согласованными и, безусловно, их можно вращать, решение чего требует алгоритмов. Однако кубик прямо посередине не учитывается, потому что на нем нет видимых наклеек и, следовательно, решения не требуется. Арифметически мы должны иметь

${ Displaystyle Р = В + Е + F + С , !}$

Но п всегда на один меньше этого (или п-размерное расширение этой формулы) на рисунках, приведенных в этой статье, потому что C (или соответствующий многогранник наибольшей размерности для более высоких измерений) не учитывается.

Волшебный 4D куб

4-куб 3⁴ виртуальная головоломка, решенная. В этой проекции не отображается одна ячейка. Положение этой ячейки - крайний передний план 4-го измерения за пределами экрана зрителя.

4-куб 3⁴ виртуальная головоломка, повернутая в 4-м измерении, чтобы показать цвет скрытой ячейки.

4-куб 3⁴ виртуальная головоломка, повернутая в нормальном трехмерном пространстве.

4-куб 3⁴ виртуальная головоломка, перемешанная.

4-куб 2⁴ виртуальная головоломка, один кубик выделен, чтобы показать, как наклейки распределяются по кубу. Обратите внимание, что на каждом кубике 2-х кубиков есть четыре наклейки.⁴ головоломка, но выделены только три, недостающий находится в скрытой ячейке.

4-куб 5⁴ виртуальная головоломка с наклейками из одного куба, сделанными так, чтобы они точно касались друг друга.

Геометрическая форма: тессеракт

Программное обеспечение Superliminal MagicCube4D реализует множество сложных головоломок четырехмерных многогранников, включая N⁴ кубики. Пользовательский интерфейс позволяет выполнять повороты и повороты в 4D, а также управлять параметрами просмотра 4D, такими как проекция в 3D, размер куба и интервал, а также размер стикера.

Superliminal Software поддерживает зал славы для рекордных решателей этой головоломки.

3⁴ 4-куб

Возможные комбинации:^[2]

${ displaystyle = { frac {24! cdot 32!} {2}} cdot { frac {16!} {2}} cdot 2 ^ {23} cdot (3!) ^ {31} cdot 3 cdot { left ({ frac {4!} {2}} right)} ^ {15} cdot 4}$

${ displaystyle sim 10 ^ {120} , !}$

2⁴ 4-куб

Возможные комбинации:^[2]

${ displaystyle {} = { frac {15!} {2}} cdot { left ({ frac {4!} {2}} right)} ^ {14} cdot 4}$

${ displaystyle {} sim 10 ^ {28} , !}$

4⁴ 4-куб

Возможные комбинации:^[2]

${ displaystyle = { frac {15!} {2}} cdot left ({ frac {4!} {2}} right) ^ {14} cdot 4 cdot { frac {64!} {2}} cdot 3 ^ {63} cdot { frac {96! Cdot 2} {2 cdot (4!) ^ {24}}} cdot { frac {2 ^ {95} cdot 64! Cdot 2} {2 cdot (8!) ^ {8}}}}$

${ Displaystyle sim 10 ^ {334} , !}$

5⁴ 4-куб

Возможные комбинации:^[2]

${ displaystyle = { frac {48!} {(6!) ^ {8}}} cdot { frac {96!} {(12!) ^ {8}}} cdot { frac {64! } {(8!) ^ {8}}} cdot { frac {24! Cdot 32!} {2}} cdot (3!) ^ {31} cdot 2 ^ {23} cdot { гидроразрыв {64!} {2}} cdot}$${ displaystyle 3 ^ {63} cdot 16! cdot left ({ frac {4!} {2}} right) ^ {15} cdot 4 cdot { frac {96!} {(4 !) ^ {24}}} cdot 2 ^ {95} cdot { frac {96!} {(4!) ^ {24}}} cdot 2 ^ {95}}$

${ displaystyle sim 10 ^ {701} , !}$

Волшебный 5D куб

5-куб 3⁵ виртуальная головоломка, близкая к виду в решенном состоянии.

5-куб 3⁵ виртуальная головоломка, зашифрованная.

5-куб 7⁵ виртуальная головоломка с выделенными частями. Остальные закрашены, чтобы облегчить понимание головоломки.

5-куб 7⁵ виртуальная головоломка, решенная.

Программная панель управления вращением 5-куба, иллюстрирующая увеличенное количество плоскости вращения возможно в 5 измерениях.

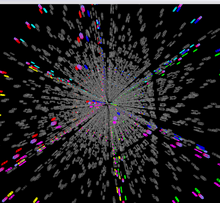
Геометрическая форма: вторгаться

Программное обеспечение Gravitation3d Magic 5D Cube способно рендерить головоломки из 5 кубиков шести размеров из 2⁵ до 7⁵. Помимо возможности перемещаться по кубу, есть элементы управления для изменения вида. К ним относятся элементы управления для вращения куба в 3-м, 4-х и 5-ти пространственном, 4-мерном и 5-мерном элементах управления перспективой, элементы управления интервалом и размером куба и стикера, аналогичные 4-мерному кубу Superliminal.

Однако 5-мерную головоломку гораздо сложнее понять на 2-мерном экране, чем 4-мерную головоломку. Важной особенностью реализации Gravitation3d является возможность выключать или выделять выбранные кубики и стикеры. Несмотря на это, сложность получаемых изображений все еще довольно серьезна, как видно из снимков экрана.

Gravitation3d поддерживает Зал Безумия для рекордных решателей этой головоломки. По состоянию на 6 января 2011 года было два успешных решения для 7⁵ размер 5-куб.^[3]

3⁵ 5-куб

Возможные комбинации:^[4]

${ displaystyle = { frac {32!} {2}} cdot 60 ^ {32} cdot { frac {80!} {2}} cdot { frac {24 ^ {80}} {2} } cdot { frac {40! cdot 80!} {2}} cdot { frac {6 ^ {80}} {2}} cdot { frac {2 ^ {40}} {2}} }$

${ displaystyle sim 10 ^ {561} , !}$

2⁵ 5-куб

Возможные комбинации:^[4]

${ displaystyle = { frac {31!} {2}} cdot 60 ^ {31}}$

${ displaystyle sim 10 ^ {89} , !}$

4⁵ 5-куб

Возможные комбинации:^[4]

${ displaystyle = { frac {31!} {2}} cdot 60 ^ {31} cdot { frac {160!} {2}} cdot { frac {12 ^ {160}} {3} } cdot { frac {320!} {24 ^ {80}}} cdot { frac {6 ^ {320}} {2}} cdot { frac {320!} {8! ^ {40} }} cdot { frac {2 ^ {320}} {2}} cdot { frac {160!} {16! ^ {10}}}}$

${ displaystyle sim 10 ^ {2075} , !}$

5⁵ 5-куб

Возможные комбинации:^[4]

${ displaystyle { begin {matrix} = { frac {32!} {2}} cdot 60 ^ {32} cdot { frac {80!} {2}} cdot { frac {24 ^ { 80}} {2}} cdot { frac {160!} {2}} cdot { frac {12 ^ {160}} {3}} cdot { frac {40! Cdot 80!} { 2}} cdot { frac {6 ^ {80}} {2}} cdot { frac {2 ^ {40}} {2}} cdot { frac {320!} {24 ^ {80} }} cdot { frac {6 ^ {320}} {2}} cdot { frac {320!} {24 ^ {80}}} cdot { frac {6 ^ {320}} {2} } cdot { frac {240!} {(6!) ^ {40}}} cdot { frac {2 ^ {240}} {2}} cdot { frac {320!} {(8! ) ^ {40}}} cdot { frac {2 ^ {320}} {2}} cdot { frac {480!} {(12!) ^ {40}}} cdot { frac {2 ^ {480}} {2}} cdot { frac {80!} {(8!) ^ {10}}} cdot { frac {160!} {(16!) ^ {10}}} cdot { frac {240!} {(24!) ^ {10}}} cdot { frac {320!} {(32!) ^ {10}}} end {matrix}}}$

${ displaystyle sim 10 ^ {5267} , !}$

6⁵ 5-куб

Возможные комбинации:^[4]

${ displaystyle { begin {matrix} = { frac {31!} {2}} cdot 60 ^ {31} cdot { frac {160!} {2}} cdot { frac {12 ^ { 160}} {3}} cdot { frac {160!} {2}} cdot { frac {12 ^ {160}} {3}} cdot { frac {320!} {24 ^ {80 }}} cdot { frac {6 ^ {320}} {2}} cdot { frac {320!} {24 ^ {80}}} cdot { frac {6 ^ {320}} {2 }} cdot { frac {640!} {24 ^ {160}}} cdot { frac {3 ^ {640}} {3}} cdot { frac {320!} {8! ^ {40 }}} cdot { frac {2 ^ {320}} {2}} cdot { frac {320!} {8! ^ {40}}} cdot { frac {2 ^ {320}} { 2}} cdot { frac {960!} {24! ^ {40}}} cdot { frac {2 ^ {960}} {2}} cdot { frac {960!} {24! ^ {40}}} cdot { frac {2 ^ {960}} {2}} cdot { frac {640!} {64! ^ {10}}} cdot { frac {960!} {96 ! ^ {10}}} cdot { frac {640!} {64! ^ {10}}} cdot { frac {160!} {16! ^ {10}}} cdot { frac {160!} {16! ^ {10}}} end {matrix}}}$

${ displaystyle sim 10 ^ {11441} , !}$

7⁵ 5-куб

Возможные комбинации:^[4]

${ displaystyle { begin {matrix} = { frac {32!} {2}} cdot 60 ^ {32} cdot { frac {80!} {2}} cdot { frac {24 ^ { 80}} {2}} cdot { frac {160!} {2}} cdot { frac {12 ^ {160}} {3}} cdot { frac {160!} {2}} cdot { frac {12 ^ {160}} {3}} cdot { frac {80! cdot 40!} {2}} cdot { frac {6 ^ {80}} {2}} cdot { frac {2 ^ {40}} {2}} cdot { frac {320!} {24 ^ {80}}} cdot { frac {6 ^ {320}} {2}} cdot { frac {320!} {24 ^ {80}}} cdot { frac {6 ^ {320}} {2}} cdot { frac {320!} {24 ^ {80}}} cdot { frac {6 ^ {320}} {2}} cdot { frac {640!} {24 ^ {160}}} cdot { frac {3 ^ {640}} {3}} cdot { гидроразрыв {320!} {24 ^ {80}}} cdot { frac {6 ^ {320}} {2}} cdot { frac {240!} {6! ^ {40}}} cdot { frac {2 ^ {240}} {2}} cdot { frac {480!} {12! ^ {40}}} cdot { frac {2 ^ {480}} {2}} cdot { frac {320!} {8! ^ {40}}} cdot { frac {2 ^ {320}} {2}} cdot { frac {240!} {6! ^ {40}} } cdot { frac {2 ^ {240}} {2}} cdot { frac {960!} {24! ^ {40}}} cdot { frac {2 ^ {960}} {2} } cdot { frac {960!} {24! ^ {40}}} cdot { frac {2 ^ {960}} {2}} cdot { frac {480!} {12! ^ {40 }}} cdot { frac {2 ^ {480}} {2}} cdot { frac {960!} {24! ^ {40}}} cdot { frac { 2 ^ {960}} {2}} cdot { frac {320!} {8! ^ {40}}} cdot { frac {2 ^ {320}} {2}} cdot { frac { 80!} {8! ^ {10}}} cdot { frac {240!} {24! ^ {10}}} cdot { frac {320!} {32! ^ {10}}} cdot { frac {160!} {16! ^ {10}}} cdot { frac {80!} {8! ^ {10}}} cdot { frac {480!} {48! ^ { 10}}} cdot { frac {960!} {96! ^ {10}}} cdot { frac {640!} {64! ^ {10}}} cdot { frac {240!} { 24! ^ {10}}} cdot { frac {960!} {96! ^ {10}}} cdot { frac {960!} {96! ^ {10}}} cdot { frac { 320!} {32! ^ {10}}} cdot { frac {640!} {64! ^ {10}}} cdot { frac {160!} {16! ^ {10}}} end {matrix}}}$

${ Displaystyle sim 10 ^ {21503} , !}$

Волшебный куб 7D

Геометрическая форма: гексеракт (6D) и вмешиваться (7D)

7-куб 5⁷ виртуальная головоломка, перемешанная.

Программа Андрея Астрелина Magic Cube 7D способна рендерить головоломки до 7 измерений в двенадцати размерах из 3⁴ до 5⁷.

По состоянию на май 2016 г. только 3⁶, 3⁷, 4⁶, и 5⁶ головоломки были решены.^[5]

Магия 120 ячеек

Виртуальная головоломка на 120 ячеек, близкая видимость в решенном состоянии

Решенная виртуальная головоломка на 120 ячеек

Геометрическая форма: 120 ячеек (также называемый гекатоникосахорон или додекаконтахорон)

120-элементная ячейка - это четырехмерная геометрическая фигура (4-многогранник ) в составе 120 додекаэдры, который, в свою очередь, представляет собой трехмерную фигуру, состоящую из 12 пятиугольники. 120-элементная ячейка является 4-мерным аналогом додекаэдра точно так же, как тессеракт (4-куб) является 4-мерным аналогом куба. 4-D 120-ячеечная программная головоломка с последовательным перемещением от Gravitation3d, таким образом, является 4-мерным аналогом Мегаминкс, 3-D пазл, имеющий форму додекаэдр.

Головоломка представлена ​​только в одном размере, то есть по три кубика по бокам, но в шести цветовых схемах разной сложности. Полная головоломка требует разного цвета для каждой ячейки, то есть 120 цветов. Такое большое количество цветов усложняет головоломку, так как некоторые оттенки довольно трудно различить. Самая простая форма - это два взаимосвязанных тора, каждый из которых образует кольцо кубов разных размеров. Полный список схем раскраски выглядит следующим образом;

• Двухцветные торы.
• 9-цветные 4-кубовые ячейки. То есть та же раскраска, что и у 4-куба.
• 9-цветный слой.
• 12-цветные кольца.
• 60-цветный антипод. Каждая пара диаметрально противоположных ячеек додекаэдра одного цвета.
• 120-цветная полная головоломка.

Элементы управления очень похожи на 4-D Magic Cube с элементами управления для 4-D перспективы, размера ячейки, размера наклейки и расстояния, а также обычного масштабирования и поворота. Кроме того, есть возможность полностью отключить группы ячеек на основе выбора торов, ячеек с 4 кубами, слоев или колец.

Gravitation3d создал «Зал славы» для решателей, которые должны предоставить файл журнала для своего решения. По состоянию на апрель 2017 года головоломка решалась двенадцать раз.^[6]

Возможные комбинации:^[7]

${ displaystyle = { frac {600!} {2}} cdot { frac {1200!} {2}} cdot { frac {720!} {2}} cdot { frac {2 ^ { 720}} {2}} cdot { frac {6 ^ {1200}} {2}} cdot { frac {12 ^ {600}} {3}}}$

${ displaystyle sim 10 ^ {8126} ,}$

Этот расчет достижимых комбинаций не был математически доказан и может считаться только верхней границей. Его вывод предполагает наличие набора алгоритмов, необходимых для выполнения всех комбинаций «минимального изменения». Нет никаких оснований предполагать, что эти алгоритмы не будут найдены, поскольку решателям головоломок удалось найти их во всех аналогичных головоломках, которые были решены до сих пор.

3x3 2D квадрат

Виртуальная головоломка 2-куб 3 × 3

Геометрическая форма: квадрат

Двумерную головоломку типа Рубика нельзя построить физически не больше, чем четырехмерную.^[8] Трехмерная головоломка может быть построена без наклеек в третьем измерении, которая в таком случае будет вести себя как двумерная головоломка, но истинная реализация головоломки остается в виртуальном мире. Показанная здесь реализация принадлежит компании Superliminal, которая называет ее 2D Magic Cube.

Головоломка не представляет большого интереса для решателей, так как ее решение довольно тривиально. В значительной степени это связано с тем, что невозможно поставить деталь на место с помощью поворота. Некоторые из самых сложных алгоритмов стандартного кубика Рубика предназначены для работы с такими поворотами, когда деталь находится в правильном положении, но не в правильной ориентации. В головоломках более высоких измерений это скручивание может принимать довольно неприятную форму, когда кусок оказывается наизнанку. Достаточно сравнить сложность головоломки 2 × 2 × 2 с головоломкой 3 × 3 (которая состоит из того же количества частей), чтобы увидеть, что эта способность вызывать повороты в более высоких измерениях во многом связана с трудностью и, следовательно, с удовлетворением. с решением, когда-либо популярный кубик Рубика.

Возможные комбинации:

${ Displaystyle = 4! , ! = 24}$

Центральные части имеют фиксированную ориентацию относительно друг друга (точно так же, как центральные части на стандартном кубе 3 × 3 × 3) и, следовательно, не учитываются при вычислении комбинаций.

Эта головоломка не совсем точный двумерный аналог кубика Рубика. Если группа операций над одним многогранником п-мерная головоломка определяется как любое вращение (п - 1) -мерный многогранник в (п - 1) -мерное пространство, то размер группы,

• для 5-куба - это вращения 4-многогранника в 4-пространстве = 8 × 6 × 4 = 192,
• для 4-куба - это вращения 3-многогранника (куба) в 3-пространстве = 6 × 4 = 24,
• для 3-куба - это вращения 2-многогранника (квадрата) в 2-пространстве = 4
• для 2-куба - это вращения 1-многогранника в 1-пространстве = 1

Другими словами, двумерная головоломка вообще не может быть перемешана, если на ходы наложены те же ограничения, что и в реальной трехмерной головоломке. Фактически, движения 2D Magic Cube - это операции отражения. Эту операцию отражения можно распространить на головоломки более высокого измерения. Для трехмерного куба аналогичной операцией будет удаление грани и замена ее наклейками, обращенными внутрь куба. Для 4-куба аналогичная операция заключается в удалении куба и его замене наизнанку.

1D проекция

Еще одна головоломка с альтернативным измерением - это вид, который можно получить в Magic Cube 3D Дэвида Вандершеля. 4-куб, проецируемый на 2D-экран компьютера, является примером общего типа п-мерная головоломка, спроецированная на (п - 2) -мерное пространство. Трехмерным аналогом этого является проецирование куба на одномерное представление, на что способна программа Вандершеля.

Вандершель сетует, что никто не утверждал, что решил одномерную проекцию этой головоломки.^[9] Однако, поскольку записи об этой загадке не ведутся, на самом деле может быть и не так, что она не решена.

1-мерная проекция куба Рубика 3x3x3, как показано в Magic Cube 3D.

Смотрите также

• Группа Кубик Рубика
• Список программного обеспечения кубика Рубика
• Список четырехмерных игр

Рекомендации

дальнейшее чтение

• Х. Дж. Камак и Т. Р. Кин, Рубик Тессеракт, доступно онлайн здесь и в архиве 25 декабря 2008 г.
• Веллеман, Д., «Тессеракт Рубика», Математический журнал, Vol. 65, № 1 (февраль 1992 г.), стр. 27–36, Математическая ассоциация Америки.
• Пиковер, C, Серфинг в гиперпространстве, pp120–122, Oxford University Press, 1999.
• Пиковер, C, Тест на интеллект пришельцев, Глава 24, Dover Publications, 2001.
• Пиковер, C, Дзен магических квадратов, кругов и звезд, pp130–133, Princeton University Press, 2001.
• Дэвид Сингмастер, Компьютерные кубисты, Июнь 2001 г. Список, поддерживаемый Singmaster, включая ссылки в 4D. Проверено 19 июня 2008 года.

внешняя ссылка

• Суперлиминал
• Анатомия d-мерного кубика Рубика от Gravitation3d
• 3D волшебный куб Дэвида Вандершеля