Безмасштабная сеть - Scale-free network

Сетевая наука
Теория
График Комплексная сеть Заражение Маленький мир Без накипи Структура сообщества Перколяция Эволюция Управляемость Рисование графика Социальный капитал Анализ ссылок Оптимизация Взаимность Закрытие Гомофилия Транзитивность Предпочтительная привязанность Теория баланса Сетевой эффект Влияние общества
Типы сетей
Информационная (вычислительная) Телекоммуникации Транспорт Социальное Научное сотрудничество Биологические Искусственный нейрон Взаимозависимый Семантический Пространственный Зависимость Поток на чипе
Графики
Функции Клика Компонент Резать Цикл Структура данных Край Петля Район Дорожка Вершина Список смежности  / матрица Список заболеваемости  / матрица Типы Двудольный Полный Режиссер Гипер Мульти Случайный Взвешенный
Метрики Алгоритмы
Центральность Степень Близость Близость PageRank Мотив Кластеризация Распределение степеней Ассортативность Расстояние Модульность Эффективность
Модели
Топология Случайный график Эрдеш – Реньи Барабаши – Альберт Фитнес модель Уоттс-Строгац Экспоненциальный случайный (ERGM) Случайный геометрический (RGG) Гиперболический (HGN) Иерархический Стохастический блок Максимальная энтропия Мягкая конфигурация Тест LFR Динамика Логическая сеть агент на основе Эпидемия /СЭР
Списки Категории
Темы Программного обеспечения Сетевые ученые Категория: Теория сетей Категория: Теория графов

А безмасштабная сеть это сеть чей распределение степеней следует за сила закона, по крайней мере, асимптотически. То есть дробь п(k) узлов в сети, имеющих k подключения к другим узлам идет на большие значения k в качестве

${ Displaystyle Р (к) сим к ^ { boldsymbol {- gamma}}}$

куда ${ displaystyle gamma}$ - параметр, значение которого обычно находится в диапазоне 2 < ${ displaystyle gamma}$ <3 (при этом второй момент (параметр масштаба ) ${ Displaystyle к ^ { boldsymbol {- gamma}}}$ бесконечно, но первый момент конечен), хотя иногда может выходить за эти границы.^[1][2]

Сообщается, что многие сети не масштабируются, хотя статистический анализ опроверг многие из этих утверждений и серьезно поставил под сомнение другие.^[3][4] Предпочтительная привязанность и фитнес-модель были предложены в качестве механизмов для объяснения предполагаемого степенного распределения степеней в реальных сетях.

История

В исследованиях сетей цитирования между научными статьями, Дерек де Солла Прайс показал в 1965 году, что количество ссылок на статьи, т. е. количество полученных ими цитат, распределение с тяжелым хвостом после Распределение Парето или же сила закона, и, таким образом, сеть цитирования не требует масштабирования. Однако он не использовал термин «безмасштабная сеть», который появился несколько десятилетий спустя. В более поздней работе в 1976 году Прайс также предложил механизм для объяснения возникновения степенных законов в сетях цитирования, который он назвал «кумулятивным преимуществом», но который сегодня более известен под названием преференциальная привязанность.

Недавний интерес к безмасштабным сетям начался в 1999 году с работы Альберт-Ласло Барабаши и коллеги из Университет Нотр-Дам кто нанес на карту топологию части Всемирной паутины,^[5] обнаружив, что некоторые узлы, которые они назвали «концентраторами», имели гораздо больше соединений, чем другие, и что сеть в целом имела степенное распределение количества ссылок, соединяющихся с узлом. Обнаружив, что несколько других сетей, включая некоторые социальные и биологические сети, также имеют распределение степеней с тяжелым хвостом, Барабаши и его сотрудники придумали термин «безмасштабная сеть» для описания класса сетей, которые демонстрируют степенное распределение степеней. Однако, изучая семь примеров сетей в социальных, экономических, технологических, биологических и физических системах, Amaral et al. среди этих семи примеров не удалось найти немасштабируемую сеть. Только один из этих примеров, сеть киноактеров, имел распределение степеней п(k) следуя степенному режиму для умеренных k, хотя в конечном итоге за этим степенным режимом последовало резкое ограничение, показывающее экспоненциальное затухание для больших k.^[6]

Барабаши и Река Альберт предложили порождающий механизм для объяснения появления степенных распределений, который они назвали "преференциальная привязанность "и который по сути совпадает с предложенным Прайсом. Аналитические решения для этого механизма (также похожие на решение Прайса) были представлены в 2000 году Дороговцевым, Мендес и Самухин ^[7] и самостоятельно Крапивским, Реднер, и Лейвраз, а позже строго доказано математиком Béla Bollobás.^[8] Примечательно, однако, что этот механизм создает только определенное подмножество сетей в безмасштабном классе, и с тех пор было обнаружено множество альтернативных механизмов.^[9]

История безмасштабных сетей также включает некоторые разногласия. На эмпирическом уровне безмасштабный характер некоторых сетей был поставлен под сомнение. Например, три брата Фалуцос считали, что Интернет имеет степенное распределение степеней на основе трассировка данные; однако было высказано предположение, что это слой 3 иллюзия, создаваемая маршрутизаторами, которые выглядят как узлы высокого уровня, скрывая при этом внутренние слой 2 структура ASes они взаимосвязаны.^[10]

На теоретическом уровне были предложены уточнения абстрактного определения безмасштабности. Например, Ли и др. (2005) недавно предложили потенциально более точную «безмасштабную метрику». Вкратце позвольте грамм быть графом с множеством ребер E, и обозначим степень вершины ${ displaystyle v}$ (то есть количество ребер, инцидентных ${ displaystyle v}$) к ${ Displaystyle deg (v)}$. Определять

${ Displaystyle s (G) = sum _ {(u, v) in E} deg (u) cdot deg (v).}$

Это максимизируется, когда узлы высокого уровня подключены к другим узлам высокого уровня. Теперь определим

${ Displaystyle S (G) = { гидроразрыва {s (G)} {s _ { max}}},}$

куда s_{Максимум} это максимальное значение s(ЧАС) за ЧАС во множестве всех графов с распределением степеней, идентичным таковому уграмм. Это дает метрику от 0 до 1, где график грамм с маленьким S(грамм) является "богатым масштабом", а график грамм с S(грамм) близко к 1 - "без масштабирования". Это определение отражает понятие самоподобие подразумевается в названии «безмасштабный».

Обзор

Есть два основных компонента, которые объясняют появление свойства безмасштабности в сложных сетях: рост и предпочтительное присоединение.^[11] Под «ростом» понимается процесс роста, при котором в течение длительного периода времени новые узлы присоединяются к уже существующей системе, сети (например, всемирной паутине, которая за 10 лет выросла на миллиарды веб-страниц). «Предпочтительное присоединение» называется новым приходящим узлом, который предпочитает подключаться к другому узлу, который уже имеет определенное количество связей с другими. Таким образом, существует более высокая вероятность того, что все больше и больше узлов свяжутся с тем узлом, который уже имеет много ссылок, что приведет к этому узлу хаб в итоге.^[5]В зависимости от сети концентраторы могут быть либо ассортативными, либо дезассортативными. Ассортативность можно найти в социальных сетях, в которых известные / известные люди будут лучше узнавать друг друга. Дизассортативность можно найти в технологических (Интернет, World Wide Web) и биологических (взаимодействие белков, метаболизм) сетях.^[11]

Характеристики

Случайная сеть (а) и безмасштабная сеть (б). В безмасштабной сети выделены более крупные концентраторы.

Сложное сетевое распределение степени случайного и безмасштабного

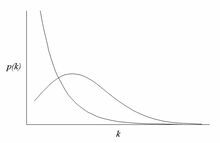
Наиболее примечательной характеристикой безмасштабной сети является относительная общность вершин со степенью, значительно превышающей среднее значение. Узлы наивысшего уровня часто называют «концентраторами», и считается, что они служат определенным целям в своих сетях, хотя это во многом зависит от домена.

Перколяция

Свойство безмасштабности сильно коррелирует с устойчивостью сети к сбоям. Оказывается, за крупными узлами следуют более мелкие. За этими меньшими узлами, в свою очередь, следуют другие узлы с еще меньшей степенью и так далее. Эта иерархия позволяет отказоустойчивой поведение. Если отказы происходят случайно и подавляющее большинство узлов имеют небольшую степень, вероятность того, что это повлияет на концентратор, почти ничтожна. Даже если произойдет отказ концентратора, сеть, как правило, не потеряет свою связность, за счет оставшихся хабов. С другой стороны, если мы выберем несколько крупных хабов и вытащим их из сети, сеть превратится в набор довольно изолированных графов. Таким образом, концентраторы являются одновременно сильной стороной и слабостью безмасштабных сетей. Эти свойства были исследованы аналитически с использованием теория перколяции Коэн и др.^[12][13] и Callaway et al.^[14] Это было доказано Коэном и др. ^[15] это для широкого диапазона сетей без масштабирования, для ${ Displaystyle 2 < гамма <3}$ критический порог перколяции, ${ displaystyle p_ {c} = 0}$. Это означает, что случайное удаление любой части узлов из сети не приведет к разрушению сети. В этом отличие от графа Эрдеша – Реньи, где ${ displaystyle p_ {c} = 1 / { bar {k}}}$, куда ${ displaystyle { bar {k}}}$ это средняя степень. Обсуждаемые выше отказы являются случайными, как обычно предполагается в теории перколяции. Однако при обобщении перколяции также на неслучайные, но целевые атаки, например, на узлы с наивысшей степенью, результаты, такие как ${ displaystyle p_ {c}}$, существенно изменится.^[13][14]Недавно был разработан новый вид сбоев в сетях, названный локализованными атаками.^[16] В этом случае случайным образом выбирается узел и удаляются его соседи и следующие ближайшие соседи до тех пор, пока не будет удалена часть 1-p узлов. Локализованные атаки делают масштабируемую сеть более уязвимой по сравнению с атаками с выкупом и pc> 0. Критические показатели просачивания в безмасштабных сетях отличаются от случайных сетей Эрдеша – Реньи. ^ [16a] Таким образом, безмасштабные сети относятся к другому классу универсальности, чем сети Эрдеша – Реньи.^[17]

Кластеризация

Еще одна важная характеристика безмасштабных сетей - это коэффициент кластеризации распределение, которое уменьшается с увеличением степени узла. Это распределение также следует степенному закону. Это означает, что узлы с низкой степенью принадлежат очень плотным подграфам, и эти подграфы связаны друг с другом через концентраторы. Рассмотрим социальную сеть, узлами которой являются люди, а ссылками - отношения знакомства между людьми. Легко видеть, что люди склонны образовывать сообщества, то есть небольшие группы, в которых каждый знает всех (такое сообщество можно представить как полный график ). Кроме того, у членов сообщества также есть несколько знакомых отношений с людьми за пределами этого сообщества. Однако некоторые люди связаны с большим количеством сообществ (например, знаменитости, политики). Этих людей можно считать хабами, ответственными за феномен маленького мира.

В настоящее время более конкретные характеристики безмасштабных сетей зависят от генеративного механизма, используемого для их создания. Например, сети, созданные с помощью предпочтительного присоединения, обычно размещают вершины с высокой степенью в середине сети, соединяя их вместе, чтобы сформировать ядро, а узлы с прогрессивной более низкой степенью составляют области между ядром и периферией. Случайное удаление даже большой части вершин очень мало влияет на общую связность сети, предполагая, что такие топологии могут быть полезны для безопасность, в то время как целевые атаки очень быстро разрушают связность. Другие безмасштабные сети, в которых вершины высокой степени размещаются на периферии, не проявляют этих свойств. Точно так же коэффициент кластеризации безмасштабных сетей может значительно варьироваться в зависимости от других топологических деталей.

Расстояние в безмасштабных сетях

Еще одна характеристика касается среднего расстояния между двумя вершинами в сети. Как и в большинстве неупорядоченных сетей, таких как сеть малого мира модели, это расстояние очень мало по сравнению с высокоупорядоченной сетью, такой как решетчатый граф. Примечательно, что некоррелированный степенной граф, имеющий 2 <γ <3, будет иметь сверхмалый диаметр d ~ ln lnN куда N - это количество узлов в сети, как доказали Коэн и Хэвлин.^[18] Таким образом, диаметр растущей безмасштабной сети на практике можно считать почти постоянным.

Сети без фрактального масштаба

Розенфельд и др. ^[19] предложил метод создания детерминированных фрактальных сетей без масштабов

Иммунизация

Вопрос о том, как иммунизировать эффективно масштабируемые свободные сети, которые представляют собой реалистичные сети, такие как Интернет и социальные сети, широко изучался. Одна из таких стратегий - иммунизировать узлы наибольшей степени, то есть целевые (преднамеренные) атаки.^[12][13] поскольку для этого случая p${ displaystyle c}$ относительно высока, и для иммунизации требуется меньше узлов. Однако во многих реальных случаях глобальная структура недоступна, а узлы наибольшей степени неизвестны. Для таких случаев разработан метод ознакомительной иммунизации.^[20] В этом случае, что довольно эффективно, узлы выбираются случайным образом, но иммунизируются их соседи. Другой, еще более эффективный метод основан на методе разбиения графа.^[21]  .

Свойства случайного графа могут изменяться или оставаться инвариантными при преобразованиях графа. Машаги А. и др., например, продемонстрировали, что преобразование, которое преобразует случайные графы в их графы с двойным ребром (или линейные графы), дает ансамбль графов с почти одинаковым распределением степеней, но со степенью корреляции и значительно более высоким коэффициентом кластеризации. Графы без масштабирования, как таковые, остаются без масштабирования при таких преобразованиях.^[22]

Примеры

Хотя многие сети реального мира считаются немасштабируемыми, доказательства часто остаются неубедительными, в первую очередь из-за растущего понимания более строгих методов анализа данных.^[3] Таким образом, безмасштабный характер многих сетей все еще обсуждается в научном сообществе. Вот несколько примеров сетей, заявленных как немасштабируемые:

• Немного Социальные сети, включая сети сотрудничества. Два примера, которые были тщательно изучены: сотрудничество киноактеров в фильмах и соавторство математиками статей.
• Многие виды компьютерная сеть, в том числе Интернет и веб-граф из Всемирная паутина.
• Графики зависимости программного обеспечения,^[23] некоторые из них описываются с помощью генеративной модели.^[24]
• Некоторые финансовые сети, такие как межбанковские платежные сети ^[25][26]
• Белково-белковое взаимодействие сети.
• Семантические сети.^[27]
• Авиационные сети.

Снимок взвешенной планарной стохастической решетки (WPSL).

Безмасштабная топология также была обнаружена в высокотемпературных сверхпроводниках.^[28] Свойства высокотемпературного сверхпроводника - соединения, в котором электроны подчиняются законам квантовой физики и движутся идеально синхронно, без трения, - по-видимому, связаны с фрактальным расположением кажущихся случайными атомами кислорода и искажением решетки.^[29]

Ячеистая структура, заполняющая пространство, взвешенная планарная стохастическая решетка (WPSL) недавно был предложен, распределение координационных чисел которого подчиняется степенному закону. Это означает, что в решетке есть несколько блоков, у которых есть удивительно большое количество соседей, с которыми они имеют общие границы. Его построение начинается с инициатора, скажем, квадрата единицы площади, и генератора, который случайным образом делит его на четыре блока. После этого генератор последовательно применяется снова и снова только к одному из доступных блоков, выбранных предпочтительно по отношению к их площадям. Это приводит к разделению квадрата на все более мелкие взаимоисключающие прямоугольные блоки. Двойник WPSL (DWPSL) получается заменой каждого блока узлом в его центре, а общая граница между блоками с ребром, соединяющим две соответствующие вершины, получается как сеть, распределение степеней которой подчиняется степенному закону.^[30][31] Причина в том, что он растет вслед за модель привязанности, основанная на посредничестве правило, которое также воплощает правило предпочтительной привязанности, но замаскировано.

Генеративные модели

Безмасштабные сети возникают не случайно. Erds и Реньи (1960) изучали модель роста графов, в которой на каждом шаге два узла выбираются равномерно случайным образом и между ними вставляется связь. Свойства этих случайные графы отличаются от свойств, присущих безмасштабным сетям, поэтому необходима модель этого процесса роста.

Наиболее широко известная генеративная модель для подмножества безмасштабных сетей - это модель Барабаши и Альберта (1999). богатые становятся богаче Генеративная модель, в которой каждая новая веб-страница создает ссылки на существующие веб-страницы с распределением вероятностей, которое не является однородным, а пропорционально текущей степени веб-страниц. Первоначально эта модель была изобретена Дерек Дж. Де Солла Прайс в 1965 г. на условиях совокупное преимущество, но не стал популярным, пока Барабаши заново не открыл результаты под своим нынешним названием (BA Модель ). Согласно этому процессу, страница с большим количеством внутренних ссылок будет привлекать больше внутренних ссылок, чем обычная страница. Это генерирует степенной закон, но результирующий граф отличается от реального веб-графа другими свойствами, такими как наличие небольших тесно связанных сообществ. Были предложены и изучены более общие модели и характеристики сети. Например, Pachon et al. (2018) предложили вариант богатые становятся богаче Генеративная модель, которая учитывает два разных правила присоединения: предпочтительный механизм присоединения и единый выбор только для самых последних узлов.^[32] Для обзора см. Книгу Дороговцева и Мендес.

Несколько иную модель генерации веб-ссылок предложили Pennock et al. (2002). Они исследовали сообщества, интересующиеся определенной темой, например домашние страницы университетов, государственных компаний, газет или ученых, и отказались от основных узлов сети. В этом случае распределение ссылок больше не было степенным, а напоминало нормальное распределение. Основываясь на этих наблюдениях, авторы предложили генеративную модель, которая сочетает предпочтительную привязанность с базовой вероятностью получения ссылки.

Другая генеративная модель - это копировать модель, изученная Kumar et al.^[33] (2000), в котором новые узлы выбирают существующий узел случайным образом и копируют часть связей существующего узла. Это также порождает степенной закон.

В рост сетей (добавление новых узлов) не является необходимым условием для создания немасштабируемой сети. Дангалчев^[34] (2004) приводит примеры создания статических безмасштабных сетей. Другая возможность (Калдарелли и др., 2002) - рассматривать структуру как статическую и рисовать связь между вершинами в соответствии с определенным свойством двух задействованных вершин. После определения статистического распределения для этих свойств вершин (пригодности) оказывается, что в некоторых случаях также статические сети развивают безмасштабные свойства.

Обобщенная безмасштабная модель

Эта статья требует внимания специалиста по математике. Пожалуйста, добавьте причина или разговаривать в этот шаблон, чтобы объяснить проблему со статьей. ВикиПроект по математике может помочь нанять эксперта. (Июнь 2009 г.)

Наблюдается всплеск активности в области моделирования безмасштабные сложные сети. Рецепт Барабаши и Альберта^[35] последовало несколько вариаций и обобщений^{[36][37][38][39][32]} и переработка предыдущих математических работ.^[40] Пока есть сила закона распределение в модели, это безмасштабная сеть, а модель этой сети - безмасштабная модель.

Функции

Многие реальные сети (приблизительно) безмасштабные и, следовательно, требуют безмасштабных моделей для их описания. В схеме Прайса для построения безмасштабной модели необходимы два ингредиента:

1. Добавление или удаление узлы. Обычно мы концентрируемся на росте сети, то есть на добавлении узлов.

2. Предпочтительная привязанность: Вероятность ${ displaystyle Pi}$ что новые узлы будут подключены к «старому» узлу.

Обратите внимание, что фитнес-модели (см. Ниже) могут работать также статически, без изменения количества узлов. Следует также иметь в виду, что тот факт, что модели «предпочтительного присоединения» приводят к появлению безмасштабных сетей, не доказывает, что это механизм, лежащий в основе эволюции реальных безмасштабных сетей, поскольку могут существовать различные механизмы в работают в реальных системах, которые, тем не менее, требуют масштабирования.

Примеры

Было предпринято несколько попыток создать безмасштабные свойства сети. Вот некоторые примеры:

Модель Барабаши – Альберта

Например, первая безмасштабная модель, Модель Барабаши – Альберта, имеет преимущественное линейное крепление ${ displaystyle Pi (k_ {i}) = { frac {k_ {i}} { sum _ {j} k_ {j}}}}$ и добавляет по одному новому узлу на каждом временном шаге.

(Обратите внимание, еще одна общая особенность ${ Displaystyle Pi (к)}$ в реальных сетях это то, что ${ Displaystyle Pi (0) neq 0}$, т.е. существует ненулевая вероятность того, что новый узел присоединится к изолированному узлу. Таким образом в целом ${ Displaystyle Pi (к)}$ имеет форму ${ Displaystyle Pi (к) = А + к ^ { альфа}}$, куда ${ displaystyle A}$ - начальная привлекательность узла.)

Двухуровневая сетевая модель

Дангалчев^[34] строит 2-литровую модель, добавляя второго порядка льготная привязанность. Привлекательность узла в модели 2-L зависит не только от количества узлов, связанных с ним, но и от количества связей в каждом из этих узлов.

${ displaystyle Pi (k_ {i}) = { frac {k_ {i} + C sum _ {(i, j)} k_ {j}} { sum _ {j} k_ {j} + C sum _ {j} k_ {j} ^ {2}}},}$

куда C - коэффициент от 0 до 1.

Модель привязанности, управляемой посредничеством (MDA)

в модель привязанности, управляемой посредничеством (MDA), новый узел идет с ${ displaystyle m}$ ребра случайным образом выбирают существующий связанный узел, а затем соединяются не с этим, а с ${ displaystyle m}$ соседей, также выбранных случайным образом. Вероятность ${ Displaystyle Pi (я)}$ что узел ${ displaystyle i}$ существующего выбранного узла

${ displaystyle Pi (i) = { frac {k_ {i}} {N}} { frac { sum _ {j = 1} ^ {k_ {i}} { frac {1} {k_ { j}}}} {k_ {i}}}.}$

Фактор ${ displaystyle { frac { sum _ {j = 1} ^ {k_ {i}} { frac {1} {k_ {j}}}} {k_ {i}}}}$ является обратной величиной гармонического среднего (IHM) степеней ${ displaystyle k_ {i}}$ соседи узла ${ displaystyle i}$. Обширные численные исследования показывают, что примерно ${ displaystyle m> 14}$ среднее значение IHM в большом ${ displaystyle N}$ предел становится константой, что означает ${ Displaystyle Пи (я) propto k_ {я}}$. Это означает, что чем выше количество ссылок (степень) у узла, тем выше его шанс получить больше ссылок, поскольку они могут быть достигнуты большим количеством способов через посредников, которые по сути воплощают интуитивную идею механизма обогащения богатых (или правило предпочтительного присоединения модель Барабаши – Альберта). Таким образом, можно увидеть, что сеть MDA следует правилу PA, но замаскировано.^[41]

Однако для ${ displaystyle m = 1}$ он описывает, как победитель получает весь механизм, поскольку мы обнаруживаем, что почти ${ displaystyle 99 \%}$ всех узлов имеет степень один, а один супербогат по степени. В качестве ${ displaystyle m}$ значение увеличивает разрыв между супербогатыми и бедными уменьшается и, как ${ displaystyle m> 14}$ мы находим механизм перехода от богатого к сверхбогатому к богатому - к богатому.

Нелинейная предпочтительная привязка

Модель Барабаши – Альберта предполагает, что вероятность ${ Displaystyle Pi (к)}$ что узел прикреплен к узлу ${ displaystyle i}$ пропорционально степень ${ displaystyle k}$ узла ${ displaystyle i}$. Это предположение включает две гипотезы: во-первых, что ${ Displaystyle Pi (к)}$ зависит от ${ displaystyle k}$, в отличие от случайных графов, в которых ${ Displaystyle Pi (к) = р}$, а во-вторых, функциональная форма ${ Displaystyle Pi (к)}$ линейно по ${ displaystyle k}$. Точная форма ${ Displaystyle Pi (к)}$ не обязательно линейный, и недавние исследования показали, что распределение степеней сильно зависит от ${ Displaystyle Pi (к)}$

Крапивский, Реднер и Лейвраз^[38] демонстрируют, что безмасштабный характер сети разрушается из-за нелинейного предпочтительного присоединения. Единственный случай, когда топология сети не требует масштабирования, - это тот случай, когда предпочтительное присоединение асимптотически линейный, т.е. ${ displaystyle Pi (k_ {i}) sim a _ { infty} k_ {i}}$ в качестве ${ displaystyle k_ {i} to infty}$. В этом случае уравнение скорости приводит к

${ displaystyle P (k) sim k ^ {- gamma} { text {with}} gamma = 1 + { frac { mu} {a _ { infty}}}.}$

Таким образом, показатель степени распределения может быть настроен на любое значение от 2 до ${ displaystyle infty}$.

Иерархическая сетевая модель

Есть еще один вид безмасштабной модели, которая растет по некоторым шаблонам, таким как иерархическая сетевая модель.^[42]

В итеративный построение, ведущее к иерархической сети. Начиная с полностью подключенного кластера из пяти узлов, мы создаем четыре идентичные реплики, соединяющие периферийные узлы каждого кластера с центральным узлом исходного кластера. Из этого получаем сеть из 25 узлов (N = 25). Повторяя тот же процесс, мы можем создать еще четыре реплики исходного кластера - четыре периферийных узла каждого из них подключаются к центральному узлу узлов, созданных на первом этапе. Это дает N = 125, и процесс может продолжаться бесконечно.

Фитнес модель

Идея в том, что связь между двумя вершинами назначается не случайно с вероятностью п равны для всех пар вершин. Скорее для каждой вершины j есть внутренняя фитнес Икс_j и связь между вершиной я и j создается с вероятностью ${ displaystyle p (x_ {i}, x_ {j})}$.^[43] В случае Всемирной торговой сети возможно реконструировать все свойства, используя в качестве пригодности страны их ВВП и принимая

${ displaystyle p (x_ {i}, x_ {j}) = { frac { delta x_ {i} x_ {j}} {1+ delta x_ {i} x_ {j}}}.}$^[44]

Гиперболические геометрические графы

Предполагая, что сеть имеет лежащую в основе гиперболическую геометрию, можно использовать структуру пространственные сети для создания безмасштабных распределений степеней. Это неоднородное распределение степеней тогда просто отражает отрицательную кривизну и метрические свойства лежащей в основе гиперболической геометрии.^[45]

Двойное преобразование ребер для создания графов без масштабирования с желаемыми свойствами

Начиная с графов без шкалы с низкой степенью корреляции и коэффициентом кластеризации, можно генерировать новые графы с гораздо более высокой степенью корреляции и коэффициентами кластеризации, применяя преобразование с двойным ребром.^[22]

Модель Uniform-Preferential-Attachment (модель UPA)

Модель УПА является вариантом модели предпочтительной привязанности (предложенной Пэчоном и др.), которая учитывает два разных правила привязанности: механизм предпочтительной привязанности (с вероятностью 1-p), который подчеркивает, что система богатых становится богаче, и единый выбор (с вероятность p) для самых последних узлов. Эта модификация интересна для изучения устойчивости безмасштабного поведения распределения степеней. Аналитически доказано сохранение асимптотически степенного распределения степеней.^[32]

Безмасштабные идеальные сети

В контексте теория сети а идеальная сеть без масштабирования это случайная сеть с распределение степеней после идеальный газ без накипи распределение плотности. Эти сети способны воспроизводить распределение по размерам городов и результаты выборов, раскрывая распределение социальных групп по размеру с помощью теории информации в сложных сетях, когда к сети применяется процесс роста конкурентных кластеров.^[46][47] В моделях безмасштабных идеальных сетей можно показать, что Номер Данбара является причиной явления, известного как "шесть ступеней расставания ' .

Новые характеристики

Для сети без масштабирования с ${ displaystyle n}$ узлы и показатель степени ${ displaystyle beta> 3}$, индуцированный подграф, построенный по вершинам со степенью больше, чем ${ Displaystyle журнал {п} раз журнал ^ {*} {п}}$ сеть без масштабирования с ${ displaystyle beta '= 2}$, почти наверняка (п.в.).^[48]

Смотрите также

• Случайный график - График, созданный случайным образом
• Модель Эрдеша – Реньи - Две тесно связанные модели для генерации случайных графов
• Нелинейная предпочтительная привязка
• Конденсация Бозе – Эйнштейна (теория сетей) - Появление в теории сетей
• Масштабная инвариантность
• Комплексная сеть - Сеть с нетривиальными топологическими особенностями
• Webgraph
• Модель Барабаши – Альберта
• Модель Бьянкони – Барабаши

Рекомендации

дальнейшее чтение

• Альберт Р .; Барабаши А.-Л. (2002). «Статистическая механика сложных сетей». Ред. Мод. Phys. 74 (1): 47–97. arXiv:cond-mat / 0106096. Bibcode:2002РвМП ... 74 ... 47А. Дои:10.1103 / RevModPhys.74.47. S2CID  60545.
• Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). «Классы сетей малого мира». PNAS. 97 (21): 11149–52. arXiv:cond-mat / 0001458. Bibcode:2000PNAS ... 9711149A. Дои:10.1073 / pnas.200327197. ЧВК  17168. PMID  11005838.
• Барабаши, Альберт-Ласло (2004). Связано: как все связано со всем остальным. ISBN  0-452-28439-2.
• Барабаши, Альберт-Ласло; Бонабо, Эрик (май 2003 г.). «Безмасштабные сети» (PDF). Scientific American. 288 (5): 50–9. Bibcode:2003SciAm.288e..60B. Дои:10.1038 / scientificamerican0503-60. PMID  12701331.
• Дан Браха; Янир Бар-Ям (2004). «Топология крупномасштабных инженерных сетей для решения проблем» (PDF). Phys. Ред. E. 69 (1): 016113. Bibcode:2004PhRvE..69a6113B. Дои:10.1103 / PhysRevE.69.016113. PMID  14995673. S2CID  1001176.
• Калдарелли Г. "Безмасштабные сети » Издательство Оксфордского университета, Оксфорд (2007).
• Caldarelli G .; Capocci A .; De Los Rios P ​​.; Муньос М.А. (2002). «Безмасштабные сети с изменяющейся внутренней пригодностью вершин». Письма с физическими проверками. 89 (25): 258702. arXiv:cond-mat / 0207366. Bibcode:2002PhRvL..89y8702C. Дои:10.1103 / PhysRevLett.89.258702. PMID  12484927.
• Р. Коэн; К. Эрез; Д. бен-Авраам; С. Хавлин (2000). «Устойчивость Интернета к случайным сбоям». Phys. Rev. Lett. 85 (21): 4626–8. arXiv:cond-mat / 0007048. Bibcode:2000ПхРвЛ..85.4626С. Дои:10.1103 / PhysRevLett.85.4626. PMID  11082612. S2CID  15372152.
• Р. Коэн; К. Эрез; Д. бен-Авраам; С. Хавлин (2001). «Разрушение Интернета при преднамеренной атаке». Phys. Rev. Lett. 86 (16): 3682–5. arXiv:cond-mat / 0010251. Bibcode:2001ПхРвЛ..86.3682С. Дои:10.1103 / PhysRevLett.86.3682. PMID  11328053. S2CID  3852896.
• Р. Коэн; К. Эрез; Д. бен-Авраам; С. Хавлин (2002). «Безмасштабные сети на решетках». Phys. Rev. Lett. 89 (21): 218701. arXiv:cond-mat / 0205613. Bibcode:2002PhRvL..89u8701R. Дои:10.1103 / Physrevlett.89.218701. PMID  12443452. S2CID  13379794.
• Дангалчев, Ч. (2004). «Модели генерации безмасштабных сетей». Physica A. 338 (3–4): 659–671. Bibcode:2004PhyA..338..659D. Дои:10.1016 / j.physa.2004.01.056.
• Дороговцев, С.Н .; Mendes, J.F.F .; Самухин, А. (2000). «Структура растущих сетей: точное решение модели Барабаши-Альберта». Phys. Rev. Lett. 85 (21): 4633–6. arXiv:cond-mat / 0004434. Bibcode:2000ПхРвЛ..85.4633Д. Дои:10.1103 / PhysRevLett.85.4633. PMID  11082614.
• Дороговцев, С.Н .; Mendes, J.F.F. (2003). Эволюция сетей: от биологических сетей к Интернету и WWW. Издательство Оксфордского университета. ISBN  0-19-851590-1.
• Дороговцев, С.Н .; Гольцев А.В .; Mendes, J.F.F. (2008). «Критические явления в сложных сетях». Ред. Мод. Phys. 80 (4): 1275–1335. arXiv:0705.0010. Bibcode:2008RvMP ... 80.1275D. Дои:10.1103 / RevModPhys.80.1275. S2CID  3174463.
• Дороговцев, С.Н .; Mendes, J.F.F. (2002). «Эволюция сетей». Успехи в физике. 51 (4): 1079–1187. arXiv:cond-mat / 0106144. Bibcode:2002AdPhy..51.1079D. Дои:10.1080/00018730110112519. S2CID  429546.
• Эрдеш, П.; Реньи, А. (1960). Об эволюции случайных графов (PDF). 5. Издание Математического института Венгерской академии наук. С. 17–61.
• Faloutsos, M .; Faloutsos, P .; Фалуцос, К. (1999). «О степенных отношениях топологии Интернет». Комп. Comm. Rev. 29 (4): 251–262. Дои:10.1145/316194.316229.
• Li, L .; Alderson, D .; Tanaka, R .; Doyle, J.C .; Виллинджер, В. (2005). «К теории безмасштабных графов: определение, свойства и значения (расширенная версия)». arXiv:cond-mat / 0501169.
• Kumar, R .; Raghavan, P .; Rajagopalan, S .; Sivakumar, D .; Tomkins, A .; Упфаль, Э. (2000). «Стохастические модели для веб-графа» (PDF). Материалы 41-го ежегодного симпозиума по основам компьютерных наук (FOCS). Редондо-Бич, Калифорния: IEEE CS Press. С. 57–65.
• Матлис, янв (4 ноября 2002 г.). «Безмасштабные сети».
• Ньюман, Марк Э.Дж. (2003). «Структура и функции сложных сетей». SIAM Обзор. 45 (2): 167–256. arXiv:cond-mat / 0303516. Bibcode:2003SIAMR..45..167N. Дои:10.1137 / S003614450342480. S2CID  221278130.
• Pastor-Satorras, R .; Веспиньяни, А. (2004). Эволюция и структура Интернета: подход статистической физики. Издательство Кембриджского университета. ISBN  0-521-82698-5.
• Pennock, D.M .; Flake, G.W .; Лоуренс, S .; Glover, E.J .; Джайлз, К. (2002). «Победители не получают все: характеристика конкуренции за ссылки в Интернете». PNAS. 99 (8): 5207–11. Bibcode:2002PNAS ... 99.5207P. Дои:10.1073 / pnas.032085699. ЧВК  122747. PMID  16578867.
• Робб, Джон. Безмасштабные сети и терроризм, 2004.
• Келлер, Э.Ф. (2005). "Пересмотр" безмасштабных "сетей". BioEssays. 27 (10): 1060–8. Дои:10.1002 / bies.20294. PMID  16163729. Архивировано из оригинал на 13.08.2011.
• Onody, R.N .; де Кастро, П.А. (2004). «Комплексное сетевое исследование бразильского футболиста». Phys. Ред. E. 70 (3): 037103. arXiv:cond-mat / 0409609. Bibcode:2004PhRvE..70c7103O. Дои:10.1103 / PhysRevE.70.037103. PMID  15524675. S2CID  31653489.
• Реувен Коэн; Шломо Хавлин (2003). «Сети без масштабирования - сверхмалые». Phys. Rev. Lett. 90 (5): 058701. arXiv:cond-mat / 0205476. Bibcode:2003PhRvL..90e8701C. Дои:10.1103 / PhysRevLett.90.058701. PMID  12633404. S2CID  10508339.
• Kasthurirathna, D .; Пиравеенан, М. (2015). «Комплексное сетевое исследование бразильского футболиста». Sci. Представитель. В прессе.