Молекулярная орбиталь - Molecular orbital

Полный ацетилен Набор молекулярных орбиталей (H – C≡C – H). В левом столбце показаны МО, занятые в основном состоянии, с орбиталью с наименьшей энергией вверху. Бело-серая линия, видимая в некоторых МО, представляет собой ось молекулы, проходящую через ядра. Орбитальные волновые функции положительны в красных областях и отрицательны в синей. В правом столбце показаны виртуальные МО, которые в основном состоянии пусты, но могут быть заняты в возбужденных состояниях.

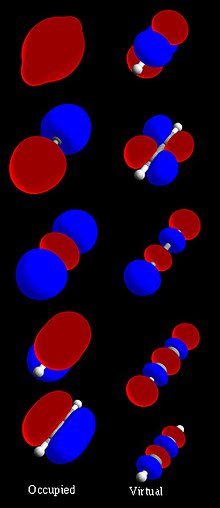
В химия, а молекулярная орбиталь это математическая функция описание места и волнообразный поведение электрон в молекула. Эта функция может использоваться для расчета химических и физических свойств, таких как вероятность нахождения электрон в любом конкретном регионе. Период, термин орбитальный был представлен Роберт С. Малликен в 1932 г. как сокращение от одноэлектронная орбитальная волновая функция.^[1] На элементарном уровне он используется для описания область, край пространства, в котором функция имеет значительную амплитуду. В изолированном атом, положение орбитальных электронов определяется функциями, называемыми атомные орбитали. Когда несколько атомов химически объединяются в молекула, расположение электронов определяется молекулой в целом, поэтому атомные орбитали объединяются, образуя молекулярные орбитали. Электроны составляющих атомов занимают молекулярные орбитали. Математически молекулярные орбитали являются приближенным решением Уравнение Шредингера для электронов в поле молекулы атомные ядра. Обычно их конструируют объединение атомные орбитали или же гибридные орбитали с каждого атом молекулы или другие молекулярные орбитали от групп атомов. Их можно количественно рассчитать с помощью Хартри – Фок или методы самосогласованного поля (SCF).

Молекулярные орбитали бывают трех типов: связывающие орбитали которые имеют энергию ниже, чем энергия атомных орбиталей, которые их сформировали, и, таким образом, способствуют химическим связям, которые удерживают молекулы вместе; разрыхляющие орбитали которые имеют энергию выше, чем энергия составляющих их атомных орбиталей, и поэтому препятствуют связыванию молекулы, и несвязывающие орбитали которые имеют ту же энергию, что и их атомные орбитали, и, таким образом, не влияют на связывание молекулы.

Обзор

Молекулярную орбиталь (МО) можно использовать для представления областей в молекула где электрон занимающие эту орбиту, вероятно, будут найдены. Молекулярные орбитали являются приближенными решениями Уравнение Шредингера для электронов в электрическом поле молекулы атомные ядра. Однако вычисление орбиталей непосредственно из этого уравнения - слишком сложная задача. Вместо этого они получены из комбинации атомных орбиталей, которые предсказывают местонахождение электрона в атоме. Молекулярная орбиталь может определять электронная конфигурация молекулы: пространственное распределение и энергия одного (или одной пары) электронов. Чаще всего МО представляет собой линейная комбинация атомных орбиталей (метод ЛКАО-МО), особенно в качественном или очень приблизительном использовании. Они неоценимы, поскольку обеспечивают простую модель связи в молекулах, понятную через теория молекулярных орбиталей.Большинство современных методов в вычислительная химия Начнем с расчета МО системы. Молекулярная орбиталь описывает поведение одного электрона в электрическом поле, создаваемом ядрами, и некоторое среднее распределение других электронов. В случае двух электронов, находящихся на одной орбитали, Принцип Паули требует, чтобы у них был противоположный спин. Обязательно это приближение, и высокоточные описания молекулярной электронной волновой функции не имеют орбиталей (см. конфигурационное взаимодействие ).

Молекулярные орбитали, как правило, делокализованы по всей молекуле. Более того, если молекула имеет элементы симметрии, ее невырожденные молекулярные орбитали либо симметричны, либо антисимметричны по отношению к любой из этих симметрий. Другими словами, применение операции симметрии S (например, отражение, вращение или инверсия) к молекулярной орбитали ψ приводит к тому, что молекулярная орбиталь остается неизменной или меняет свой математический знак на противоположный: Sψ = ± ψ. В планарных молекулах, например, молекулярные орбитали либо симметричны (сигма ) или антисимметричный (число Пи ) относительно отражения в плоскости молекулы. Если также рассматривать молекулы с вырожденной орбитальной энергией, более общее утверждение, что молекулярные орбитали образуют основы для неприводимые представления молекулы группа симметрии держит.^[2] Свойства симметрии молекулярных орбиталей означают, что делокализация является неотъемлемой чертой теории молекулярных орбиталей и делает ее фундаментально отличной от (и дополняющей) теория валентной связи, в котором связи рассматриваются как локализованные электронные пары с учетом резонанс чтобы учесть делокализацию.

В отличие от этих адаптированных к симметрии канонический молекулярные орбитали, локализованные молекулярные орбитали могут быть сформированы путем применения определенных математических преобразований к каноническим орбиталям. Преимущество этого подхода состоит в том, что орбитали будут более точно соответствовать «связям» молекулы, как это показано структурой Льюиса. Недостатком является то, что уровни энергии этих локализованных орбиталей больше не имеют физического смысла. (Обсуждение в оставшейся части этой статьи будет сосредоточено на канонических молекулярных орбиталях. Для дальнейшего обсуждения локализованных молекулярных орбиталей см .: орбиталь естественной связи и сигма-пи и эквивалентные орбитальные модели.)

Формирование молекулярных орбиталей

Молекулярные орбитали возникают в результате разрешенных взаимодействий между атомные орбитали, которые допустимы, если симметрии (определяемые из теория групп ) атомных орбиталей совместимы друг с другом. Эффективность атомных орбитальных взаимодействий определяется из перекрывать (мера того, насколько хорошо две орбитали конструктивно взаимодействуют друг с другом) между двумя атомными орбиталями, что важно, если атомные орбитали близки по энергии. Наконец, количество образованных молекулярных орбиталей должно быть равно количеству атомных орбиталей в атомах, которые объединяются в молекулу.

Качественное обсуждение

Для неточного, но качественно полезного обсуждения молекулярной структуры, молекулярные орбитали могут быть получены из "Линейная комбинация атомных орбиталей, метод молекулярных орбиталей " анзац. Здесь молекулярные орбитали выражаются как линейные комбинации из атомные орбитали.^[3]

Линейные комбинации атомных орбиталей (ЛКАО)

Молекулярные орбитали были впервые введены Фридрих Хунд^[4][5] и Роберт С. Малликен^[6][7] в 1927 и 1928 гг.^[8][9] В линейная комбинация атомных орбиталей или приближение "ЛКАО" для молекулярных орбиталей было введено в 1929 г. Сэр Джон Леннард-Джонс.^[10] В его новаторской статье показано, как получить электронную структуру фтор и кислород молекулы из квантовых принципов. Этот качественный подход к теории молекулярных орбиталей является частью начала современного квантовая химия. Линейные комбинации атомных орбиталей (LCAO) могут использоваться для оценки молекулярных орбиталей, которые образуются при связывании между составляющими молекулу атомами. Подобно атомной орбитали, уравнение Шредингера, описывающее поведение электрона, может быть также построено для молекулярной орбитали. Линейные комбинации атомных орбиталей или суммы и разности атомных волновых функций обеспечивают приближенные решения Уравнения Хартри – Фока которые соответствуют приближению независимых частиц молекулярной Уравнение Шредингера. Для простых двухатомных молекул полученные волновые функции математически представлены уравнениями

${displaystyle Psi = c_ {a} psi _ {a} + c_ {b} psi _ {b}}$

${displaystyle Psi ^ {*} = c_ {a} psi _ {a} -c_ {b} psi _ {b}}$

куда ${displaystyle Psi}$ и ${displaystyle Psi ^ {*}}$ - молекулярные волновые функции для связывающих и разрыхляющих молекулярных орбиталей соответственно, ${displaystyle psi _ {a}}$ и ${displaystyle psi _ {b}}$ - атомные волновые функции от атомов a и b соответственно, и ${displaystyle c_ {a}}$ и ${displaystyle c_ {b}}$ - регулируемые коэффициенты. Эти коэффициенты могут быть положительными или отрицательными, в зависимости от энергий и симметрии отдельных атомных орбиталей. Когда два атома становятся ближе друг к другу, их атомные орбитали перекрываются, создавая области с высокой электронной плотностью, и, как следствие, между двумя атомами образуются молекулярные орбитали. Атомы удерживаются вместе за счет электростатического притяжения между положительно заряженными ядрами и отрицательно заряженными электронами, занимающими связывающие молекулярные орбитали.^[11]

Связующие, разрыхляющие и несвязывающие МО

Когда атомные орбитали взаимодействуют, результирующая молекулярная орбиталь может быть трех типов: связывающая, разрыхляющая или несвязывающая.

Склеивание МО:

• Связующие взаимодействия между атомными орбиталями являются конструктивными (синфазными) взаимодействиями.
• Связующие МО имеют меньшую энергию, чем атомные орбитали, которые объединяются для их образования.

Антибондинговые МО:

• Разрыхляющие взаимодействия между атомными орбиталями являются деструктивными (противофазными) взаимодействиями с узловая плоскость где волновая функция разрыхляющей орбитали между двумя взаимодействующими атомами равна нулю.
• Антисвязывающие МО имеют более высокую энергию, чем атомные орбитали, которые объединяются для их образования.

Несвязывающие МО:

• Несвязывающие МО являются результатом отсутствия взаимодействия между атомными орбиталями из-за отсутствия совместимых симметрий.
• Несвязывающие МО будут иметь ту же энергию, что и атомные орбитали одного из атомов в молекуле.

Метки сигма и пи для МО

Тип взаимодействия между атомными орбиталями может быть дополнительно классифицирован по меткам симметрии молекулярных орбиталей σ (сигма), π (пи), δ (дельта), φ (фи), γ (гамма) и т. Д. Это греческие буквы, соответствующие к атомным орбиталям s, p, d, f и g соответственно. Число узловых плоскостей, содержащих межъядерную ось между рассматриваемыми атомами, равно нулю для σ МО, одному для π, двум для δ, трех для φ и четырем для γ.

σ симметрия

МО с σ-симметрией возникает в результате взаимодействия либо двух атомных s-орбиталей, либо двух атомных p_z-орбитали. МО будет иметь σ-симметрию, если орбиталь симметрична относительно оси, соединяющей два ядерных центра, межъядерной оси. Это означает, что вращение МО вокруг межъядерной оси не приводит к изменению фазы. Орбиталь σ *, сигма-антисвязывающая орбиталь, также сохраняет ту же фазу при вращении вокруг межъядерной оси. Орбиталь σ * имеет узловую плоскость, которая находится между ядрами и перпендикулярна межъядерной оси.^[12]

π-симметрия

МО с π-симметрией возникает в результате взаимодействия двух атомов p_Икс орбитали или p_у орбитали. МО будет иметь π-симметрию, если орбиталь асимметрична относительно вращения вокруг межъядерной оси. Это означает, что вращение МО вокруг межъядерной оси приведет к фазовому переходу. Существует одна узловая плоскость, содержащая межъядерную ось, если реальные орбитали считаются.

Орбиталь π *, разрыхляющая пи-орбиталь, также будет вызывать изменение фазы при вращении вокруг межъядерной оси. Орбиталь π * также имеет вторую узловую плоскость между ядрами.^{[12][13][14][15]}

δ симметрия

МО с δ-симметрией возникает в результате взаимодействия двух атомных d_ху или d_{Икс²-у²} орбитали. Поскольку эти молекулярные орбитали содержат d-атомные орбитали с низкой энергией, они видны в переходный металл комплексы. Связывающая δ-орбиталь имеет две узловые плоскости, содержащие межъядерную ось, а δ * разрыхляющая орбиталь также имеет третью узловую плоскость между ядрами.

φ симметрия

Соответствующим образом выровненные атомные f-орбитали перекрываются, образуя фи-молекулярную орбиталь (фи-связь)

Химики-теоретики предположили, что возможны связи более высокого порядка, такие как phi-связи, соответствующие перекрытию f-атомных орбиталей. По состоянию на 2005 год существует только один известный пример молекулы, предположительно содержащей фи-связь (связь U-U в молекуле U₂ ).^[16]

Симметрия Герада и Унгерада

Для молекул, обладающих центром инверсии (центросимметричные молекулы ) существуют дополнительные метки симметрии, которые могут быть применены к молекулярным орбиталям. Центросимметричные молекулы включают:

• Гомоядерный диатомия, X₂
• Восьмигранный, БЫВШИЙ₆
• Квадратный плоский, БЫВШИЙ₄.

К нецентросимметричным молекулам относятся:

• Гетероядерный диатомия, XY
• Тетраэдр, БЫВШИЙ₄.

Если инверсия через центр симметрии в молекуле приводит к одним и тем же фазам для молекулярной орбитали, то говорят, что МО имеет симметрию Герада (g), от немецкого слова, означающего четный. Если инверсия через центр симметрии в молекуле приводит к фазовому изменению для молекулярной орбитали, тогда говорят, что МО имеет ungerade (u) симметрию, от немецкого слова, обозначающего нечетное. Для связывающей МО с σ-симметрией орбиталь σ_грамм (s '+ s' 'симметрична), а у разрыхляющей МО с σ-симметрией орбиталь σ_ты, поскольку инверсия s '- s' 'антисимметрична. для связывающей МО с π-симметрией орбиталь равна π_ты поскольку инверсия через центр симметрии для приведет к изменению знака (две атомные p-орбитали находятся в фазе друг с другом, но два лепестка имеют противоположные знаки), в то время как разрыхляющая МО с π-симметрией равна π_грамм потому что инверсия через центр симметрии для не приведет к смене знака (две p-орбитали антисимметричны по фазе).^[12]

Диаграммы МО

Качественный подход к анализу МО использует диаграмму молекулярных орбиталей для визуализации связывающих взаимодействий в молекуле. На диаграммах этого типа молекулярные орбитали представлены горизонтальными линиями; чем выше линия, тем выше энергия орбитали, а вырожденные орбитали размещаются на одном уровне с промежутком между ними. Затем электроны, которые должны быть размещены на молекулярных орбиталях, размещаются один за другим с учетом принципа исключения Паули и правила максимальной множественности Хунда (только 2 электрона с противоположными спинами на орбитали; поместите столько неспаренных электронов на одну уровень энергии, насколько это возможно, прежде чем начинать объединять их). Для более сложных молекул подход волновой механики теряет полезность в качественном понимании связи (хотя все еще необходим для количественного подхода). Некоторые свойства:

• Базовый набор орбиталей включает те атомные орбитали, которые доступны для молекулярно-орбитальных взаимодействий, которые могут быть связывающими или разрыхляющими.
• Количество молекулярных орбиталей равно количеству атомных орбиталей, включенных в линейное расширение или базисный набор.
• Если молекула обладает некоторой симметрией, вырожденные атомные орбитали (с той же атомной энергией) группируются в линейные комбинации (называемые адаптированные к симметрии атомные орбитали (SO)), которые принадлежат представление из группа симметрии, Итак волновые функции которые описывают группу, известны как адаптированные к симметрии линейные комбинации (SALC).
• Количество молекулярных орбиталей, принадлежащих одному представлению группы, равно количеству адаптированных к симметрии атомных орбиталей, принадлежащих этому представлению.
• В рамках конкретного представление, адаптированные к симметрии атомные орбитали смешиваются больше, если их атомные уровни энергии ближе.

Общую процедуру построения диаграммы молекулярных орбиталей для достаточно простой молекулы можно резюмировать следующим образом:

1. Назначьте молекуле точечную группу.

2. Найдите формы SALC.

3. Расположите SALC каждого молекулярного фрагмента в порядке возрастания энергии, сначала отметив, происходят ли они из s, п, или же d орбитали (и расставьте их по порядку s < п < d), а затем их количество межъядерных узлов.

4. Объедините SALC одного типа симметрии из двух фрагментов, и из N SALC образуют N молекулярных орбиталей.

5. Оцените относительные энергии молекулярных орбиталей из соображений перекрытия и относительных энергий родительских орбиталей и нарисуйте уровни на диаграмме энергетических уровней молекулярных орбиталей (показывая происхождение орбиталей).

6. Подтвердите, исправьте и пересмотрите этот качественный порядок, выполнив расчет молекулярных орбиталей с помощью коммерческого программного обеспечения.^[17]

Связь на молекулярных орбиталях

Орбитальное вырождение

Молекулярные орбитали называются вырожденными, если они имеют одинаковую энергию. Например, в гомоядерных двухатомных молекулах первых десяти элементов молекулярные орбитали, полученные из p_Икс и п_у атомные орбитали приводят к двум вырожденным связывающим орбиталям (с низкой энергией) и двум вырожденным антисвязывающим орбиталям (с высокой энергией).^[11]

Ионные связи

Когда разность энергий между атомными орбиталями двух атомов достаточно велика, орбитали одного атома вносят почти весь вклад в связывающие орбитали, а орбитали другого атома вносят почти весь вклад в разрыхляющие орбитали. Таким образом, фактически ситуация такова, что один или несколько электронов были перенесены от одного атома к другому. Это называется (в основном) ионная связь.

Заказ облигаций

Порядок связи или количество связей в молекуле можно определить путем объединения числа электронов на связывающих и разрыхляющих молекулярных орбиталях. Пара электронов на связывающей орбитали создает связь, тогда как пара электронов на антисвязывающей орбитали отрицает связь. Например, N₂, с восемью электронами на связывающих орбиталях и двумя электронами на разрыхляющих орбиталях, имеет порядок связи три, что составляет тройную связь.

Прочность сцепления пропорционален порядку связи - большее количество связей дает более стабильную связь - и длина облигации обратно пропорционально ему - более сильная связь короче.

Есть редкие исключения из требования наличия у молекулы положительного порядка связи. Хотя быть₂ имеет порядок связи 0 согласно анализу МО, есть экспериментальные свидетельства очень нестабильного Be₂ молекула, имеющая длину связи 245 пм и энергию связи 10 кДж / моль.^[12][18]

HOMO и LUMO

Наивысшую занятую молекулярную орбиталь и самую низкую незанятую молекулярную орбиталь часто называют HOMO и LUMO соответственно. Разница энергий HOMO и LUMO называется щелью HOMO-LUMO. Это понятие часто вызывает путаницу в литературе, и к нему следует относиться с осторожностью. Его значение обычно находится между основной щелью (разностью между потенциалом ионизации и сродством к электрону) и оптической щелью. Кроме того, разрыв HOMO-LUMO можно отнести к сыпучему материалу. запрещенная зона или транспортный разрыв, который обычно намного меньше фундаментального.

Примеры

Гомоядерная диатомия

Гомоядерные двухатомные МО содержат равные вклады от каждой атомной орбитали в базисном наборе. Это показано на гомоядерных двухатомных диаграммах МО для H₂, Он₂, и Ли₂, все из которых содержат симметричные орбитали.^[12]

ЧАС₂

Электрон волновые функции для Орбитальный одиночного атома водорода (слева и справа) и соответствующие связывающие (внизу) и разрыхляющие (вверху) молекулярные орбитали H₂ молекула. В реальная часть волновой функции - синяя кривая, а мнимая часть это красная кривая. Красные точки отмечают расположение ядер. Волновая функция электрона колеблется в соответствии с Волновое уравнение Шредингера, а орбитали - его стоячие волны. Частота стоячей волны пропорциональна кинетической энергии орбиты. (Этот сюжет представляет собой одномерный срез трехмерной системы.)

В качестве простого примера МО рассмотрим электроны в водород молекула, H₂ (видеть диаграмма молекулярных орбиталей ), с двумя атомами, обозначенными H 'и H ". Атомные орбитали с наименьшей энергией, 1s' и 1s", не преобразуются в соответствии с симметрией молекулы. Однако следующие симметрии адаптированные атомные орбитали делают:

Симметричная комбинация (называемая связывающей орбиталью) имеет меньшую энергию, чем базисные орбитали, а антисимметричная комбинация (называемая разрушение орбитальная) выше. Потому что H₂ Молекула имеет два электрона, оба они могут двигаться по связывающей орбитали, что делает систему более низкой по энергии (следовательно, более стабильной), чем два свободных атома водорода. Это называется Ковалентная связь. В ордер на облигации равно количеству связывающих электронов минус количество разрыхляющих электронов, разделенное на 2. В этом примере есть 2 электрона на связывающей орбитали и ни одного на разрыхляющей орбитали; порядок связи равен 1, и между двумя атомами водорода существует одинарная связь.

Он₂

С другой стороны, рассмотрим гипотетическую молекулу He₂ с атомами, обозначенными He 'и He ". Как и в случае H₂, атомные орбитали с самой низкой энергией - это единицы и единицы », и они не преобразуются в соответствии с симметрией молекулы, в то время как атомные орбитали, адаптированные к симметрии, преобразуются. Симметричная комбинация - связывающая орбиталь - имеет меньшую энергию, чем базисные орбитали , а антисимметричная комбинация - разрыхляющая орбиталь - выше.₂, с двумя валентными электронами, He₂ имеет четыре в нейтральном основном состоянии. Два электрона заполняют связывающую орбиталь с более низкой энергией σ_грамм(1s), а оставшиеся два заполняют более высокоэнергетическую разрыхляющую орбиталь σ_ты* (1 с). Таким образом, результирующая электронная плотность вокруг молекулы не поддерживает образование связи между двумя атомами; без стабильной связи, удерживающей атомы вместе, молекула не может существовать. С другой стороны, существует два связывающих электрона и два разрыхляющих электрона; следовательно, порядок связи равен 0, и связи не существует (молекула имеет одно связанное состояние, поддерживаемое потенциалом Ван-дер-Ваальса).^{[нужна цитата ]}

Ли₂

Дилитий Ли₂ формируется из перекрытия атомных орбиталей 1s и 2s (базисный набор) двух атомов Li. Каждый атом Li вносит три электрона для связывающих взаимодействий, и шесть электронов заполняют три МО с наименьшей энергией σ_грамм(1с), σ_ты* (1s), а σ_грамм(2 с). Используя уравнение для порядка связи, было обнаружено, что дилитий имеет порядок связи, равный единице, одинарную связь.

благородные газы

Рассматривая гипотетическую молекулу He₂, поскольку базис атомных орбиталей такой же, как и в случае H₂, мы обнаруживаем, что и связывающая, и разрыхляющая орбитали заполнены, так что у пары нет энергетического преимущества. HeH будет иметь небольшое энергетическое преимущество, но не такое большое, как H₂ + 2 He, поэтому молекула очень нестабильна и существует недолго, прежде чем разложиться на водород и гелий. В общем, мы обнаруживаем, что такие атомы, как He, которые имеют полноэнергетические оболочки, редко связываются с другими атомами. Кроме недолговечных Комплексы Ван-дер-Ваальса, их очень мало соединения благородных газов известен.

Гетероядерная диатомия

В то время как МО для гомоядерных двухатомных молекул содержат равные вклады от каждой взаимодействующей атомной орбитали, МО для гетероядерных диатомовых молекул содержат разные атомные орбитальные вклады. Орбитальные взаимодействия для создания связывающих или антисвязывающих орбиталей в гетероядерных диатомиях происходят, если существует достаточное перекрытие между атомными орбиталями, что определяется их симметрией и сходством орбитальных энергий.

HF

В фтороводород Перекрытие HF между H 1s и F 2s орбиталями разрешено симметрией, но разница в энергии между двумя атомными орбиталями не позволяет им взаимодействовать для создания молекулярной орбитали. Перекрытие между H 1s и F 2p_z орбитали также разрешена симметрия, и эти две атомные орбитали имеют небольшое энергетическое разделение. Таким образом, они взаимодействуют, приводя к созданию МО σ и σ * и молекулы с порядком связи 1. Поскольку HF нецентросимметричная молекула, метки симметрии g и u не применяются к ее молекулярным орбиталям.^[19]

Количественный подход

Для получения количественных значений молекулярной уровни энергии, необходимо иметь такие молекулярные орбитали, что конфигурационное взаимодействие (CI) быстро сходится к полный CI предел. Наиболее распространенный метод получения таких функций - это Метод Хартри – Фока, который выражает молекулярные орбитали как собственные функции из Оператор Фока. Обычно эту проблему решают путем расширения молекулярных орбиталей как линейных комбинаций Гауссовы функции сосредоточен на атомные ядра (видеть линейная комбинация атомных орбиталей и базисный набор (химия) ). Уравнение для коэффициентов этих линейные комбинации является обобщенным собственное значение уравнение, известное как Уравнения Рутана, которые фактически являются частным представлением уравнения Хартри – Фока. Существует ряд программ, в которых можно проводить квантово-химические расчеты МО, в том числе Спартанский и HyperChem.

Простые объяснения часто предполагают, что экспериментальные молекулярные орбитальные энергии могут быть получены методами ультрафиолетовая фотоэлектронная спектроскопия для валентных орбиталей и Рентгеновская фотоэлектронная спектроскопия для основных орбиталей.Это, однако, неверно, поскольку в этих экспериментах измеряется энергия ионизации, разница в энергии между молекулой и одним из ионов, возникающая в результате удаления одного электрона. Энергии ионизации приблизительно связаны с орбитальными энергиями соотношением Теорема Купманса. Хотя соответствие между этими двумя значениями может быть близким для некоторых молекул, в других случаях оно может быть очень плохим.

Рекомендации