Дерево Пифагора (фрактал) - Pythagoras tree (fractal)

В Дерево пифагора это самолет фрактал построен из квадраты. Изобретенный нидерландский язык математика учитель Альберт Э. Босман в 1942 г.,[1] он назван в честь древнегреческий математик Пифагор потому что каждая тройка соприкасающихся квадратов включает в себя прямоугольный треугольник, в конфигурации, традиционно используемой для изображения теорема Пифагора.Если самый большой квадрат имеет размер L × L, все дерево Пифагора плотно умещается в коробке размером 6L × 4L.[2][3] Более мелкие детали дерева напоминают Кривая Леви C.
Строительство
Построение дерева Пифагора начинается с квадрат. На этом квадрате построены два квадрата, каждый из которых уменьшен в линейном масштабе √2/ 2, так что углы квадратов попарно совпадают. Затем применяется та же процедура. рекурсивно к двум меньшим квадратам, до бесконечности. На рисунке ниже показаны первые несколько итерации в процессе строительства.[2][3]
 |  |  |  |
| Заказ 0 | Заказ 1 | Заказ 2 | Заказ 3 |
Площадь
Итерация п в конструкции добавляет 2п квадраты площади , для общей площади 1. Таким образом, может показаться, что площадь дерева неограниченно растет в пределах п → ∞. Однако некоторые из квадратов перекрываются, начиная с итерации 5-го порядка, и дерево фактически имеет конечную площадь, потому что оно помещается в блок 6 × 4.[2]
Легко показать, что площадь А дерева Пифагора должно быть в диапазоне 5 <А <18, который можно сузить дополнительными усилиями. Кажется, мало что известно о реальной стоимостиА.
Изменение угла
Интересный набор вариаций можно создать, сохранив равнобедренный треугольник, но изменив базовый угол (90 градусов для стандартного дерева Пифагора). В частности, когда базовый полуугол установлен на (30 °) = arcsin (0,5), легко видеть, что размер квадратов остается постоянным. Первое перекрытие происходит на четвертой итерации. Общая полученная модель - это ромбитогексагональная черепица, массив шестиугольников, ограниченных квадратами построения.
 | 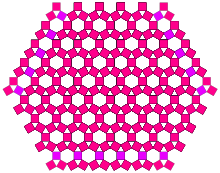 |
| Заказ 4 | Заказ 10 |
В пределах, когда половина угла составляет 90 градусов, очевидно, что перекрытия нет, и общая площадь в два раза больше площади основного квадрата. Было бы интересно узнать, существует ли алгоритмическая взаимосвязь между значением основного половинного угла и итерацией, на которой квадраты сначала перекрывают друг друга.
История
Дерево Пифагора было впервые построено Альбертом Э. Босманом (1891–1961). нидерландский язык учитель математики, в 1942 г.[2][4]
Смотрите также
Рекомендации
- ^ «Архивная копия». Архивировано из оригинал на 2009-01-18. Получено 2012-03-10.CS1 maint: заархивированная копия как заголовок (ссылка на сайт).
- ^ а б c d Wisfaq.nl.
- ^ а б Pourahmadazar, J .; Ghobadi, C .; Нуриния, Дж. (2011). "Новые модифицированные пифагорейские фрактальные монопольные антенны на основе дерева для приложений СШП". Антенны IEEE и письма о беспроводном распространении. Нью-Йорк: IEEE. 10: 484–487. Bibcode:2011IAWPL..10..484P. Дои:10.1109 / LAWP.2011.2154354.
- ^ Arsetmathesis.nl В архиве 2009-01-18 на Wayback Machine
внешняя ссылка
- Галерея деревьев Пифагора
- Интерактивный генератор с кодом
- «Дерево Пифагора с разной геометрией, а также в 3D». Архивировано из оригинал на 2008-01-15.
- Дерево Пифагора Энрике Зелени по программе Эрик В. Вайсштейн, The Вольфрам Демонстрационный проект.
- Вайсштейн, Эрик В. «Дерево Пифагора». MathWorld.
- Трехмерное дерево Пифагора
- Скрипт MatLab для создания дерева Пифагора
- Pourahmadazar, J .; Ghobadi, C .; Нуриния, Дж. (2011). "Новые модифицированные пифагорейские фрактальные монопольные антенны на основе дерева для приложений СШП". Антенны IEEE и письма о беспроводном распространении. Нью-Йорк: IEEE. 10: 484–487. Bibcode:2011IAWPL..10..484P. Дои:10.1109 / LAWP.2011.2154354.





