Теорема об остатке - Residue theorem

В комплексный анализ, дисциплина в математике, теорема о вычетахиногда называют Теорема Коши о вычетах, это мощный инструмент для оценки линейные интегралы из аналитические функции по замкнутым кривым; его часто можно использовать для вычисления реальных интегралов и бесконечная серия также. Он обобщает Интегральная теорема Коши и Интегральная формула Коши. С геометрической точки зрения это частный случай обобщенная теорема Стокса.

утверждение

Заявление выглядит следующим образом:

Иллюстрация постановки.

Позволять $U$ быть односвязный открытое подмножество из комплексная плоскость содержащий конечный список точек $а 1, ..., а п$ , и $ж$ функция определена и голоморфный на $U \{а1, ..., ап}$ . Позволять $γ$ быть закрытым выпрямляемая кривая в $U$ который не соответствует ни одному из $а k$ , и обозначим номер намотки из $γ$ около $а k$ от $Я(γ, а k)$ . Линейный интеграл от $ж$ около $γ$ равно $2 π я$ умноженная на сумму остатки из $ж$ в точках, каждая засчитывается столько раз, сколько $γ$ вьется вокруг точки:

{ displaystyle oint _ { gamma} f (z) , dz = 2 pi i sum _ {k = 1} ^ {n} operatorname {I} ( gamma, a_ {k}) operatorname {Res} (f, a_ {k}).}

Если $γ$ это положительно ориентированный простая замкнутая кривая, $Я(γ, а k) = 1$ если $а k$ находится в интерьере $γ$ , и 0, если нет, поэтому

{ displaystyle oint _ { gamma} f (z) , dz = 2 pi i sum operatorname {Res} (f, a_ {k})}

с суммой сверх тех $а k$ внутри $γ$ .^[1]

Связь теоремы о вычетах с теоремой Стокса дается формулой Теорема Жордана. Генерал плоская кривая $γ$ сначала нужно свести к набору простых замкнутых кривых ${γ я}$ общая сумма эквивалентна $γ$ в целях интеграции; это сводит проблему к нахождению интеграла от $ж дз$ вдоль жордановой кривой $γ я$ с интерьером $V$ . Требование, чтобы $ж$ быть голоморфным на $U0 = U \ {аk}$ эквивалентно утверждению, что внешняя производная $d (ж дз) = 0$ на $U 0$ . Таким образом, если две плоские области $V$ и $W$ из $U$ заключить то же подмножество ${а j}$ из ${а k}$ , регионы $V \ W$ и $W \ V$ полностью лежать в $U 0$ , и, следовательно

{ displaystyle int _ {V smallsetminus W} d (f , dz) - int _ {W smallsetminus V} d (f , dz)}

хорошо определена и равна нулю. Следовательно, контурный интеграл $ж дз$ вместе $γ j = \partialV$ равна сумме набора интегралов по путям $λ j$ , каждый из которых охватывает произвольно малую область вокруг одного $а j$ - остатки $ж$ (с точностью до условного множителя $2 π я$ ) в ${а j}$ . Подводя итоги ${γ j}$ , получаем окончательное выражение контурного интеграла через числа намоток ${Я(γ, а k)}$ .

Для вычисления вещественных интегралов теорема о вычетах используется следующим образом: подынтегральное выражение расширяется на комплексную плоскость и вычисляются его вычеты (что обычно легко), а часть вещественной оси расширяется до замкнутой кривой прикрепив полукруг в верхней или нижней полуплоскости, образуя полукруг. Затем интеграл по этой кривой может быть вычислен с помощью теоремы о вычетах. Часто полукруглая часть интеграла будет стремиться к нулю по мере увеличения радиуса полукруга, оставляя только действительную часть интеграла, ту, которая нас интересовала изначально.

Примеры

Интеграл по действительной оси

Интегральный

{ displaystyle int _ {- infty} ^ { infty} { frac {e ^ {itx}} {x ^ {2} +1}} , dx}

Контур

C

.

возникает в теория вероятности при расчете характеристическая функция из Распределение Коши. Он сопротивляется приемам элементарной исчисление но можно оценить, выразив его как предел контурные интегралы.

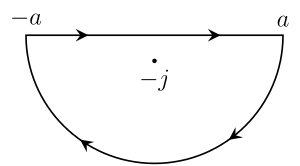
Предположим $т > 0$ и определим контур $C$ что идет по настоящий линия от $- а$ к $а$ а затем против часовой стрелки по полукругу с центром в 0 из $а$ к $- а$ . Взять $а$ быть больше 1, так что воображаемый единица измерения $я$ заключен в кривую. Теперь рассмотрим контурный интеграл

{ displaystyle int _ {C} {f (z)} , dz = int _ {C} { frac {e ^ {itz}} {z ^ {2} +1}} , dz.}

поскольку $е итц$ является вся функция (не имея особенности в любой точке комплексной плоскости) эта функция имеет особенности только там, где знаменатель $z 2 + 1$ равно нулю. поскольку $z 2 + 1 = (z + я)(z - я)$ , это происходит только там, где $z = я$ или $z = - я$ . Только одна из этих точек находится в области, ограниченной этим контуром. Потому что $ж (z)$ является

{ displaystyle { begin {align} { frac {e ^ {itz}} {z ^ {2} +1}} & = { frac {e ^ {itz}} {2i}} left ({ frac {1} {zi}} - { frac {1} {z + i}} right) & = { frac {e ^ {itz}} {2i (zi)}} - { frac { e ^ {itz}} {2i (z + i)}}, end {выравнивается}}}

то остаток из $ж (z)$ в $z = я$ является

{ displaystyle operatorname {Res} limits _ {z = i} f (z) = { frac {e ^ {- t}} {2i}}.}

Тогда согласно теореме о вычетах имеем

{ Displaystyle int _ {C} е (z) , dz = 2 pi i cdot operatorname {Res} limits _ {z = i} f (z) = 2 pi i { frac {e ^ {- t}} {2i}} = pi e ^ {- t}.}

Контур $C$ можно разделить на прямую часть и криволинейную дугу, так что

{ Displaystyle int _ { mathrm {прямо}} f (z) , dz + int _ { mathrm {arc}} f (z) , dz = pi e ^ {- t} ,}

и поэтому

{ displaystyle int _ {- a} ^ {a} f (z) , dz = pi e ^ {- t} - int _ { mathrm {arc}} f (z) , dz.}

Используя некоторые оценки, у нас есть

{ displaystyle left | int _ { mathrm {arc}} { frac {e ^ {itz}} {z ^ {2} +1}} , dz right | leq pi a cdot sup _ { text {arc}} left | { frac {e ^ {itz}} {z ^ {2} +1}} right | leq pi a cdot sup _ { text {arc }} { frac {1} {| z ^ {2} +1 |}} leq { frac { pi a} {a ^ {2} -1}},}

и

{ displaystyle lim _ {a to infty} { frac { pi a} {a ^ {2} -1}} = 0.}

Оценка числителя следует, поскольку $т > 0$ , а для комплексных чисел $z$ по дуге (лежащей в верхней полуплоскости) аргумент $φ$ из $z$ лежит между 0 и $π$ . Так,

{ Displaystyle left | е ^ {itz} right | = left | e ^ {it | z | ( соз varphi + я грех varphi)} right | = left | e ^ {- t | z | sin varphi + it | z | cos varphi} right | = e ^ {- t | z | sin varphi} leq 1.}

Следовательно,

{ displaystyle int _ {- infty} ^ { infty} { frac {e ^ {itz}} {z ^ {2} +1}} , dz = pi e ^ {- t}.}

Если $т < 0$ то аналогичный аргумент с дугой $C'$ что крутится вокруг $- я$ скорее, чем $я$ показывает, что

Контур

C'

.

{ displaystyle int _ {- infty} ^ { infty} { frac {e ^ {itz}} {z ^ {2} +1}} , dz = pi e ^ {t},}

и наконец у нас есть

{ displaystyle int _ {- infty} ^ { infty} { frac {e ^ {itz}} {z ^ {2} +1}} , dz = pi e ^ {- left | t right |}.}

(Если $т = 0$ то интеграл немедленно поддается элементарным методам исчисления и его значение равно $π$ .)

Бесконечная сумма

Дело в том, что $π детская кроватка (πz)$ имеет простые полюсы с остатком 1 в каждом целом числе, может использоваться для вычисления суммы

{ displaystyle displaystyle sum _ {n = - infty} ^ { infty} f (n).}

Рассмотрим, например, $ж (z) = z -2$ . Позволять $Γ N$ прямоугольник, являющийся границей $[- N - 1 / 2, N + 1 / 2] 2$ с положительной ориентацией, с целым числом $N$ . По формуле вычета

{ displaystyle { frac {1} {2 pi i}} int _ { Gamma _ {N}} f (z) pi cot ( pi z) , dz = operatorname {Res} ограничивает _ {z = 0} + sum _ {n = -N atop n neq 0} ^ {N} n ^ {- 2}.}

Левая часть обращается в ноль при $N \to \infty$ поскольку подынтегральное выражение имеет порядок $О (N -2)$ . С другой стороны,^[2]

{ displaystyle { frac {z} {2}} cot left ({ frac {z} {2}} right) = 1-B_ {2} { frac {z ^ {2}} {2 !}} + cdots qquad}

где Число Бернулли

{ displaystyle B_ {2} = { frac {1} {6}}.}

(По факту, $z / 2 детская кроватка (z / 2) = iz / 1 - е - iz - iz / 2$ .) Таким образом, остаток $Res z =0$ является $- π 2 / 3$ . Мы приходим к выводу:

{ displaystyle sum _ {n = 1} ^ { infty} { frac {1} {n ^ {2}}} = { frac { pi ^ {2}} {6}}}

что является доказательством Базельская проблема.

Тот же трюк можно использовать для определения суммы Серия Эйзенштейна:

{ displaystyle pi cot ( pi z) = lim _ {N to infty} sum _ {n = -N} ^ {N} (z-n) ^ {- 1}.}

Мы принимаем $ж (z) = (ш - z) -1$ с участием $ш$ нецелое число, и мы покажем это для $ш$ . Сложность в этом случае состоит в том, чтобы показать обращение в нуль контурного интеграла на бесконечности. У нас есть:

{ displaystyle int _ { Gamma _ {N}} { frac { pi cot ( pi z)} {z}} , dz = 0}

так как подынтегральная функция является четной функцией, и поэтому вклады контура в левой полуплоскости и контура в правой компенсируют друг друга. Таким образом,

{ displaystyle int _ { Gamma _ {N}} f (z) pi cot ( pi z) , dz = int _ { Gamma _ {N}} left ({ frac {1 } {wz}} + { frac {1} {z}} right) pi cot ( pi z) , dz}

стремится к нулю как $N \to \infty$ .

Смотрите также

Заметки

^ Уиттакер и Ватсон 1920, п. 112, §6.1.
^ Уиттакер и Ватсон 1920, п. 125, §7.2. Обратите внимание, что число Бернулли ${ displaystyle B_ {2n}}$ обозначается ${ displaystyle B_ {n}}$ в книге Уиттакера и Ватсона.

использованная литература

Альфорс, Ларс (1979). Комплексный анализ. Макгроу Хилл. ISBN 0-07-085008-9.
Линделёф, Эрнст Л. (1905). Le Calcul des Résidus et ses Applications à la théorie des fonctions (На французском). Издания Жака Габа (опубликовано в 1989 г.). ISBN 2-87647-060-8.
Митринович, Драгослав; Кечкич, Йован (1984). Метод вычетов Коши: теория и приложения. Издательство Д. Рейдел. ISBN 90-277-1623-4.
Уиттакер, Э. Т.; Уотсон, Г.Н. (1920). Курс современного анализа (3-е изд.). Издательство Кембриджского университета.

внешние ссылки

[1] Уиттакер и Ватсон 1920, п. 112, §6.1.

[2] Уиттакер и Ватсон 1920, п. 125, §7.2. Обратите внимание, что число Бернулли ${ displaystyle B_ {2n}}$ обозначается ${ displaystyle B_ {n}}$ в книге Уиттакера и Ватсона.

[1]

[2]