Маленький мир эксперимент - Small-world experiment

Модель «шести степеней разделения»

В маленький мир эксперимент состоял из нескольких экспериментов, проведенных Стэнли Милгрэм и другие исследователи, изучающие средняя длина пути для социальные сети людей в Соединенных Штатах.[1] Исследование было новаторским, поскольку предполагало, что человеческое общество - это маленький мир сеть, характеризующаяся короткими длинами путей. Эксперименты часто ассоциируются с фразой "шесть ступеней расставания ", хотя сам Милгрэм не использовал этот термин.

Исторический контекст проблемы маленького мира

Гульельмо Маркони предположения, основанные на его радиоработах в начале 20-го века, которые были сформулированы в его работе 1909 года. Нобелевская премия адрес,[2] возможно вдохновил[нужна цитата ] Венгерский автор Фриджес Каринти написать задачу найти другого человека, с которым он не мог быть связан максимум через пять человек.[3] Это, пожалуй, самое раннее упоминание концепции шесть ступеней расставания, и поиск ответа на проблему маленького мира.

Математик Манфред Кохен и политолог Итиэль де Сола бассейн написал математическую рукопись «Контакты и влияния», работая в Парижский университет в начале 1950-х, когда Милгрэм посетил их и сотрудничал в их исследованиях. Их неопубликованная рукопись распространялась среди ученых более 20 лет до публикации в 1978 году. В ней формально сформулирована механика социальные сети и исследовали математические последствия этого (включая степень связанности). Рукопись оставила нерешенными многие важные вопросы о сетях, и одним из них было количество степеней разделения в реальных социальных сетях.

Милгрэм принял вызов по возвращении из Парижа, что привело к экспериментам, описанным в «Проблема маленького мира» в майском номере 1967 (устав) популярного журнала. Психология сегодня, с более строгой версией статьи, представленной в Социометрия два года спустя. В Психология сегодня Статья вызвала огромную огласку экспериментов, которые хорошо известны сегодня, спустя долгое время после того, как большая часть основополагающей работы была забыта.

Эксперимент Милгрэма был задуман в эпоху, когда несколько независимых потоков сходились на идее о том, что мир становится все более взаимосвязанным. Михаил Гуревич провел плодотворную работу в своем эмпирическом исследовании структуры социальных сетей в своей Массачусетский технологический институт докторская диссертация под пулом. Математик Манфред Кохен, австриец, принимавший участие в государственник городской дизайн, экстраполировал эти эмпирические результаты в математическую рукопись, Контакты и влияния, делая вывод о том, что в популяции американского размера без социальной структуры «практически очевидно, что любые два человека могут контактировать друг с другом с помощью по крайней мере двух посредников. В [социально] структурированном населении это менее вероятно, но все же кажется вероятным . И, возможно, для всего населения мира, вероятно, понадобится только еще один связующий индивид ».[нужна цитата ] Впоследствии они построили Моделирование Монте-Карло основан на данных Гуревича, который признал, что для моделирования социальной структуры необходимы как слабые, так и сильные связи знакомства. Моделирование, выполнявшееся на более медленных компьютерах 1973 года, было ограниченным, но все же позволяло предсказать, что среди населения США существуют более реалистичные три степени разделения, что предвещало открытия Милгрэма.

Милгрэм еще раз вернулся к экспериментам Гуревича в сети знакомств, когда он провел широко разрекламированный набор экспериментов, начавшихся в 1967 г. Гарвардский университет. Одна из самых известных работ Милгрэма - исследование послушания и авторитета, широко известное как эксперимент Милгрэма.[4] Более ранняя связь Милгрэма с Пулом и Коченом была вероятным источником его интереса к растущей взаимосвязи между людьми. Интервью Гуревича послужили основой для его экспериментов с маленьким миром.

Милгрэм стремился разработать эксперимент, который мог бы ответить на проблему маленького мира. Это был тот же феномен, о котором писал писатель. Фриджес Каринти в 1920-х годах, документируя широко распространенную веру в Будапешт что люди были разделены шестью степенями социального контакта. Это наблюдение, в свою очередь, было основано на фундаментальных демографический работы статистов, которые оказали большое влияние на дизайн восточноевропейских городов того периода. Математик Бенуа Мандельброт родился в Польше и много путешествовал по Восточной Европе, знал эмпирические правила статистиков, а также был коллегой Пула, Кохена и Милграма в Парижском университете в начале 1950-х годов (Кохен пригласил Мандельброта работать в Институт перспективных исследований и позже IBM в США.). Этот круг исследователей был очарован взаимосвязанностью и «социальным капиталом» социальных сетей.

Результаты исследования Милгрэма показали, что людей в Соединенных Штатах в среднем связывают примерно три дружеских узы, без размышлений о глобальных связях; он никогда не использовал фразу «шесть степеней разделения». Поскольку Психология сегодня статья придала экспериментам широкую огласку, Милграм, Кочен и Каринти были неверно приписаны происхождению понятия «шесть степеней»; наиболее вероятным популяризатором фразы «шесть степеней разделения» является Джон Гуаре, который приписал Маркони значение «шесть».

Эксперимент

Эксперимент Милгрэма возник из желания узнать больше о вероятности того, что два случайно выбранных человека узнают друг друга.[5] Это один из способов взглянуть на проблему маленького мира. Альтернативный взгляд на проблему - представить население как социальную сеть и попытаться найти средняя длина пути между любыми двумя узлами. Эксперимент Милгрэма был разработан для измерения этих длин пути путем разработки процедуры подсчета количества связей между любыми двумя людьми.

Основная процедура

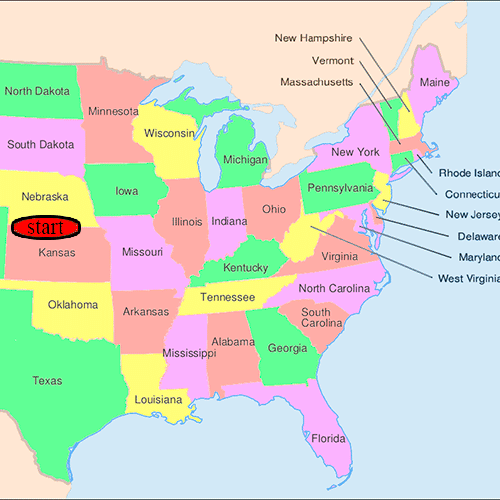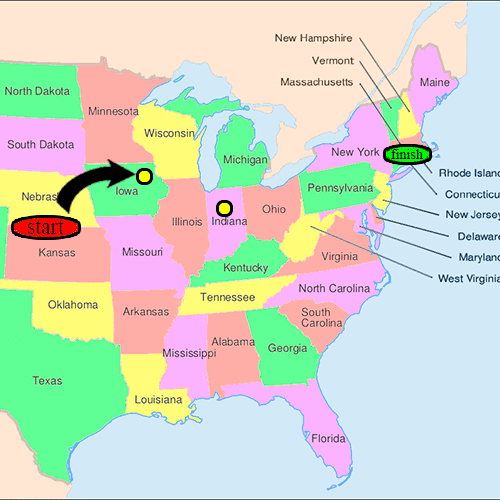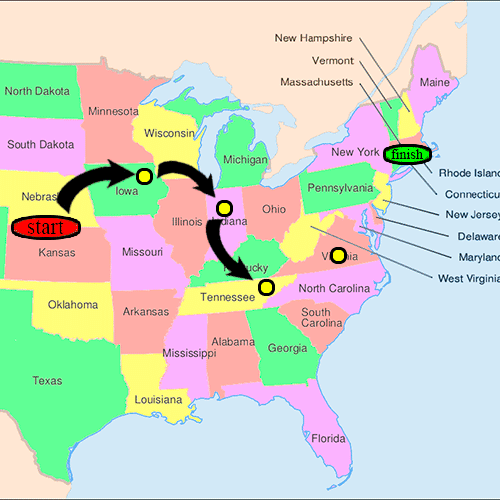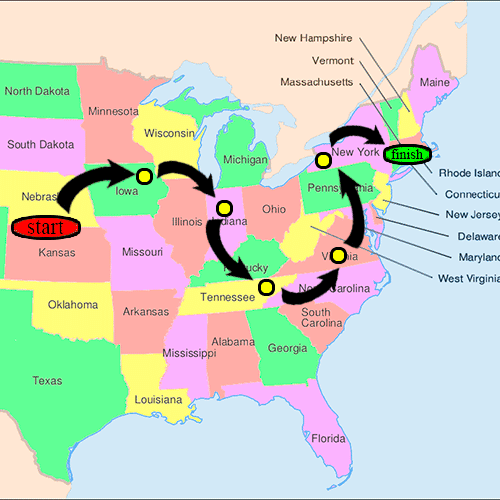
Один из возможных путей сообщения в эксперименте Стэнли Милграма «Маленький мир».
  1. Хотя эксперимент проходил в нескольких вариантах, Милгрэм обычно выбирал людей из городов США. Омаха, Небраска, и Уичито, Канзас, быть отправными точками и Бостон, Массачусетс, чтобы быть конечной точкой цепочки корреспонденции. Эти города были выбраны потому, что считалось, что они представляют собой большое расстояние в Соединенных Штатах как в социальном, так и в географическом плане.[3]
  2. Информационные пакеты изначально отправлялись «случайно» выбранным людям в Омахе или Уичито. Они включали письма, в которых подробно описывались цели исследования, и основная информация о целевом контактном лице в Бостоне. Кроме того, он содержал список, в котором они могли написать свое имя, а также визитные карточки для ответов, которые были предварительно адресованы в Гарвард.
  3. После получения приглашения к участию получателя спросили, знает ли он лично контактное лицо, указанное в письме. Если так, человек должен был переслать письмо непосредственно этому человеку. Для целей данного исследования «личное» знание кого-либо определялось как знакомство с ним по имени.
  4. В более вероятном случае, когда человек лично не знал цель, он должен был думать о друге или родственнике, который с большей вероятностью знал цель. Затем им было предложено подписать свое имя в списке и переслать пакет этому человеку. Открытка была также отправлена ​​исследователям из Гарварда, чтобы они могли отслеживать продвижение цепочки к цели.
  5. Когда и если посылка в конечном итоге достигла контактного лица в Бостоне, исследователи могли изучить список, чтобы подсчитать, сколько раз он был пересылается от человека к человеку. Кроме того, для посылок, которые так и не дошли до места назначения, входящие открытки помогли определить точку разрыва в цепочке.[нужна цитата ]

Результаты

Вскоре после начала экспериментов к мишеням начали поступать письма, а исследователи получали открытки от респондентов. Иногда пакет достигал цели всего за один или два перехода, тогда как некоторые цепочки состояли из девяти или десяти ссылок. Однако серьезной проблемой было то, что люди часто отказывались передавать письмо, и поэтому цепочка так и не доходила до места назначения. В одном случае 232 из 296 писем так и не дошли до места назначения.[5]

Однако 64 письма в конечном итоге дошли до адресата. Среди этих цепочек средняя длина пути упал около пяти с половиной или шести. Следовательно, исследователи пришли к выводу, что людей в Соединенных Штатах разделяют в среднем около шести человек. Хотя сам Милгрэм никогда не использовал фразу "шесть ступеней расставания ", эти результаты, вероятно, способствовали его широкому признанию.[3]

В эксперименте, в котором было разослано 160 писем, 24 достигли цели в его доме в Шарон, Массачусетс. Из этих 24 писем 16 были переданы жертве одним и тем же человеком, торговцем одеждой Милграма по имени «мистер Джейкобс». Из тех, что достигли цели в его офисе, более половины пришло от двух других мужчин.[6]

Исследователи использовали открытки, чтобы качественно изучить типы создаваемых цепочек. Как правило, пакет быстро достигал непосредственной географической близости, но почти случайным образом обводил цель до тех пор, пока не находил ближайших друзей цели.[5] Это говорит о том, что участники сильно отдавали предпочтение географическим характеристикам при выборе подходящего следующего человека в цепочке.

Критика

Существует ряд методологических критических замечаний по поводу эксперимента с маленьким миром, которые предполагают, что средняя длина пути может быть меньше или больше, чем ожидал Милгрэм. Здесь резюмируются четыре таких критических замечания:

  1. Джудит Кляйнфельд утверждает[7] что исследование Милграма страдает от систематической ошибки отбора и отсутствия ответов из-за способа набора участников и высоких показателей невыполнения. Во-первых, «начинающие» были выбраны не случайно, поскольку они были привлечены через рекламу, специально предназначенную для людей, считающих себя имеющими хорошие связи. Другая проблема связана с истощением. Если предположить, что у каждого человека в цепочке постоянная часть отсутствия ответа, более длинные цепочки будут недостаточно представлены, потому что более вероятно, что они столкнутся с нежелательным участником. Следовательно, эксперимент Милгрэма должен недооценивать истинную среднюю длину пути. Было предложено несколько методов для исправления этих оценок; один использует вариант анализ выживаемости чтобы учесть информацию о длине прерванных цепочек и, таким образом, уменьшить систематическую ошибку при оценке средних степеней разделения.[8]
  2. Одна из ключевых особенностей методологии Милграма состоит в том, что участников просят выбрать человека, которого они знают, который, скорее всего, знает целевого человека. Но во многих случаях участник может не знать, кто из его друзей, скорее всего, знает цель. Таким образом, поскольку участники эксперимента Милгрэма не имеют топологической карты социальной сети, они могут фактически отправлять пакет подальше от цели, а не отправлять его по сети. кратчайший путь. Это, скорее всего, увеличит длину маршрута из-за завышенной оценки среднего количества связей, необходимых для соединения двух случайных людей. Всезнающий планировщик путей, имея доступ к полному социальному графу страны, сможет выбрать кратчайший путь, который в целом короче, чем путь, созданный жадный алгоритм который принимает только местные решения.
  3. Описание гетерогенных социальных сетей до сих пор остается открытым вопросом. Хотя в течение ряда лет исследований не проводилось, в 1998 г. Дункан Уоттс и Стивен Строгац опубликовал в журнале прорывную статью Природа. Марк Бьюкенен сказал: «Их статья вызвала бурю дальнейшей работы во многих областях науки» (Nexus, стр. 60, 2002). См. Книгу Уоттса по этой теме: Шесть степеней: наука соединенного века.
  4. Некоторые сообщества, такие как Сентинельский, полностью изолированы, разрушая в остальном глобальные цепочки. Как только эти люди обнаруживаются, они остаются более «далекими» от подавляющего большинства мира, поскольку у них мало экономических, семейных или социальных контактов с миром в целом; до того, как их обнаружат, они ни в какой степени не отделены от остального населения. Однако эти популяции неизменно малы, что снижает статистическую значимость.

В дополнение к этой методологической критике обсуждаются концептуальные вопросы. Один из них касается социальной значимости цепочек косвенных контактов разной степени разделения. Большая часть формальных и эмпирических работ сосредоточена на процессах распространения, но литература по проблеме маленького мира также часто иллюстрирует актуальность исследования на примере (аналогичном эксперименту Милгрэма) целевого поиска, в котором начальный человек пытается получить какой-то ресурса (например, информации) от целевого лица, используя ряд посредников для достижения этого целевого человека. Однако существует мало эмпирических исследований, показывающих, что для такого направленного поиска действительно используются косвенные каналы длиной около шести степеней разделения или что такие процессы поиска более эффективны по сравнению с другими средствами (например, поиском информации в каталоге).[9]

Оказать влияние

Социальные науки

Переломный момент от Малькольм Гладуэлл, на основе статей, изначально опубликованных в Житель Нью-Йорка,[10] развивает концепцию «воронки». Гладуэлл резюмирует социологические исследования, в которых утверждается, что феномен шести степеней зависит от нескольких выдающихся людей ("разъемы ") с большими сетями контактов и друзей: эти хабы затем служат посредниками между огромным большинством людей, которые в остальном слабо связаны.

Однако недавние исследования влияния феномена малого мира на передачу болезней показали, что из-за сильно связанный характер социальных сетей в целом, удаление этих хабов из популяции обычно мало влияет на среднюю длину пути через график (Barrett et al., 2005).[нужна цитата ]

Математики и актеры

Было обнаружено, что более мелкие сообщества, такие как математики и актеры, тесно связаны цепочками личных или профессиональных ассоциаций. Математики создали Число Эрдеша описать их расстояние от Пол Эрдёш на основе общих публикаций. Аналогичное упражнение проделано и с актером. Кевин Бэкон и другие актеры, которые вместе с ним снимались в фильмах - последнее усилие информирует игру "Шесть градусов Кевина Бэкона ". Есть также комбинированные Число Эрдеша-Бэкона, для актеров-математиков и математиков-актеров. Игроки популярной азиатской игры Идти опишите их расстояние от великого игрока Хонинбо Сюсаку подсчитывая их Число сюсаку, который учитывает степени разделения в играх, которые сыграли игроки.[11]

Текущие исследования проблемы маленького мира

Вопрос о маленьком мире по-прежнему является популярной темой исследований сегодня, и многие эксперименты все еще проводятся. Например, Питер Доддс, Роби Мухамад и Дункан Уоттс провели первую крупномасштабную репликацию эксперимента Милгрэма с участием 24 163 цепочек электронных писем и 18 целей по всему миру.[12]

Доддс и другие. также обнаружили, что средняя длина цепи была примерно шесть, даже с учетом истирания. Аналогичный эксперимент с использованием популярных социальных сетей в качестве среды был проведен в Университет Карнеги Меллон. Результаты показали, что очень мало сообщений действительно дошло до места назначения. Однако критика, относящаяся к эксперименту Милгрэма, в значительной степени относится и к текущему исследованию.[нужна цитата ]

Сетевые модели

В 1998 г. Дункан Дж. Уоттс и Стивен Строгац от Корнелл Университет опубликовал первую сетевую модель феномена маленького мира. Они показали, что сети как из природного, так и искусственного мира, такие как электрические сети и нейронная сеть C. elegans, показать феномен маленького мира. Уоттс и Строгац показали, что, начиная с регулярной решетки, добавление небольшого количества случайных связей уменьшает диаметр - самый длинный прямой путь между любыми двумя вершинами в сети - с очень длинного до очень короткого. Исследование было первоначально вдохновлено попытками Уоттса понять синхронизацию крикет щебетать, которые демонстрируют высокую степень координации на больших расстояниях, как будто насекомых ведет невидимый проводник. Математическая модель, разработанная Уоттсом и Строгатцем для объяснения этого явления, с тех пор применяется в самых разных областях. По словам Уоттса:[13]

Я думаю, что со мной связались люди практически из всех областей, помимо английской литературы. Я получил письма от математиков, физиков, биохимиков, нейрофизиологов, эпидемиологов, экономистов, социологов; от специалистов по маркетингу, информационным системам, гражданскому строительству, а также от коммерческих предприятий, использующих концепцию маленького мира для сетевых целей в Интернете.

Как правило, их модель показывала истину в Марк Грановеттер Наблюдение за тем, что социальную сеть скрепляет «сила слабых связей». Хотя конкретная модель с тех пор была обобщена Джон Кляйнберг, он остается каноническим примером в области сложные сети. В теория сети, идея представлена ​​в сеть малого мира Модель исследована достаточно широко. Действительно, несколько классических результатов в случайный граф Теория показывает, что даже сети без реальной топологической структуры демонстрируют феномен маленького мира, который математически выражается как диаметр сети, увеличивающийся с логарифмом числа узлов (а не пропорциональный числу узлов, как в случае для решетки). Этот результат аналогично отображается на сети со степенным распределением степеней, например безмасштабные сети.

В Информатика, явление тесного мира (хотя обычно его так не называют) используется при разработке безопасных одноранговых протоколов, новых алгоритмов маршрутизации для Интернета и для этого случая беспроводные сети и алгоритмы поиска сетей связи всех видов.

В популярной культуре

Социальные сети пронизывают массовую культуру в США и других странах. В частности, понятие шесть градусов стал частью коллективного сознания. Социальные сети такие как Facebook значительно расширили возможности взаимодействия в онлайн-пространстве за счет применения концепций социальных сетей.

Смотрите также

использованная литература

  1. ^ Милгрэм, Стэнли (май 1967). «Проблема маленького мира». Психология сегодня. Издательская компания "Зифф-Дэвис".
  2. ^ Гульельмо Маркони, 1909 г., Нобелевская лекция, Беспроводная телеграфная связь.
  3. ^ а б c Барабаши, Альберт-Ласло В архиве 2005-03-04 на Wayback Machine. 2003. "Связано: как все связано со всем остальным и что это значит для бизнеса, науки и повседневной жизни. В архиве 2007-01-03 на Wayback Machine "Нью-Йорк: Плюм.
  4. ^ «Архивная копия». Архивировано из оригинал на 2008-07-31. Получено 2008-09-14.CS1 maint: заархивированная копия как заголовок (ссылка на сайт)
  5. ^ а б c Трэверс, Джеффри; Милгрэм, Стэнли (1969). «Экспериментальное исследование проблемы малого мира». Социометрия. 32 (4): 425–443. Дои:10.2307/2786545. JSTOR  2786545.
  6. ^ Гладуэлл, Малькольм. «Закон немногих». Переломный момент. Маленький Браун. С. 34–38.
  7. ^ Кляйнфельд, Джудит (март 2002 г.). "Шесть градусов: городской миф?". Психология сегодня. Sussex Publishers, LLC. Получено 15 июня, 2011.
  8. ^ Шнеттлер, Себастьян. 2009. «Маленький мир на глиняных ногах? Сравнение эмпирических исследований малого мира с критериями передовой практики». Социальные сети, 31 (3), стр. 179-189, Дои:10.1016 / j.socnet.2008.12.005
  9. ^ Шнеттлер, Себастьян. 2009. "Структурированный обзор 50-летнего исследования малого мира" Социальные сети, 31 (3), стр. 165-178, Дои:10.1016 / j.socnet.2008.12.004
  10. ^ Шесть степеней Лоис Вайсберг В архиве 2007-06-30 на Wayback Machine
  11. ^ Лэрд, Рой. «Какой у вас« номер сюсаку? »« American Go E-Journal ». Американская ассоциация го (24 июля 2011 г.). Получено 29 ноября 2017.
  12. ^ «Экспериментальное исследование поиска в глобальных социальных сетях». Наука 8 августа 2003 г .: Vol. 301 нет. 5634 с. 827-829 DOI: 10.1126 / science.1081058
  13. ^ Шульман, Полли (1 декабря 1998 г.). «От Мухаммеда Али до бабушки Роуз». Журнал DISCOVER. Получено 13 августа 2010.

внешние ссылки