Вывод преобразований Лоренца. - Derivations of the Lorentz transformations

Часть серии по
Пространство-время
Специальная теория относительности Общая теория относительности
Концепции пространства-времени Пространственно-временное многообразие Принцип эквивалентности Преобразования Лоренца Пространство Минковского
Общая теория относительности Введение в общую теорию относительности Математика общей теории относительности Уравнения поля Эйнштейна
Классическая гравитация Введение в гравитацию Закон всемирного тяготения Ньютона
Соответствующая математика Четыре вектора Выводы теории относительности Диаграммы пространства-времени Дифференциальная геометрия Искривленное пространство-время Математика общей теории относительности Топология пространства-времени

Есть много способов получить Преобразования Лоренца используя различные физические принципы, начиная от Уравнения Максвелла к Эйнштейну постулаты специальной теории относительности, и математический инструменты, начиная с элементарная алгебра и гиперболические функции, к линейная алгебра и теория групп.

В этой статье представлены несколько простых из них, которым можно следовать в контексте специальная теория относительности, для простейшего случая буста Лоренца в стандартной конфигурации, т.е. два инерциальные системы отсчета движущиеся относительно друг друга с постоянной (равномерной) относительная скорость меньше чем скорость света, и используя Декартовы координаты таким образом Икс и Икс'Оси коллинеарны.

Преобразование Лоренца

В основных отраслях современная физика, а именно общая теория относительности и его широко применимое подмножество специальная теория относительности, а также релятивистская квантовая механика и релятивистская квантовая теория поля, то Преобразование Лоренца это правило преобразования, при котором все четырехвекторный и тензоры содержащий физические величины преобразовать из одного точка зрения другому.

Яркими примерами таких четырех векторов являются четыре позиции и четыре импульса из частица, и для поля то электромагнитный тензор и тензор энергии-импульса. Математически именно то, что эти объекты трансформируются в соответствии с преобразованием Лоренца, определяет их как векторы и тензоры; видеть тензор для определения.

Учитывая компоненты четырех векторов или тензоров в некотором кадре, «правило преобразования» позволяет определять измененные компоненты тех же четырех векторов или тензоров в другом кадре, которые могут быть увеличены или ускорены по сравнению с исходным кадром. "Повышение" не следует смешивать с пространственный перевод, скорее он характеризуется относительная скорость между кадрами. Само правило преобразования зависит от относительного движения кадров. В простейшем случае два инерциальные системы относительная скорость между ними входит в правило преобразования. За вращающиеся системы отсчета или вообще неинерциальные системы отсчета необходимо больше параметров, включая относительную скорость (величину и направление), ось вращения и угол поворота.

Историческое прошлое

Обычное лечение (например, Альберт Эйнштейн оригинальная работа) основана на неизменности скорости света. Однако это не обязательно является отправной точкой: действительно (как показано, например, во втором томе Курс теоретической физики к Ландо и Лифшиц ), на кону стоит местонахождение взаимодействий: предполагается, что влияние, которое, скажем, одна частица оказывает на другую, не может передаваться мгновенно. Следовательно, существует теоретическая максимальная скорость передачи информации, которая должна быть инвариантной, и оказывается, что эта скорость совпадает со скоростью света в вакууме. Ньютон сам назвал идею действия на расстоянии философски «абсурдной» и считал, что гравитация должна передаваться неким агентом согласно определенным законам.^[1]

Михельсон и Морли в 1887 году разработал эксперимент с использованием интерферометра и полупрозрачного зеркала, который оказался достаточно точным, чтобы обнаружить поток эфира. Система зеркал отражала свет обратно в интерферометр. Если бы имел место дрейф эфира, он вызвал бы фазовый сдвиг и изменение интерференции, которое было бы обнаружено. Однако фазового сдвига обнаружено не было. Отрицательный исход Эксперимент Майкельсона-Морли оставил понятие эфира (или его дрейфа) подорванным. Вследствие этого возникло недоумение относительно того, почему свет, очевидно, ведет себя как волна, без какой-либо обнаруживаемой среды, через которую может распространяться волновая активность.

В статье 1964 г.^[2] Эрик Кристофер Зееман показал, что причинность сохранение свойства, условие, которое в математическом смысле более слабое, чем инвариантность скорости света, достаточно, чтобы гарантировать, что преобразования координат являются преобразованиями Лоренца. В статье Нормана Гольдштейна аналогичный результат показан с использованием инерционность (сохранение временных линий), а не причинность.^[3]

Физические принципы

Эйнштейн основал свою теорию специальной теории относительности на двух фундаментальных постулаты. Во-первых, все физические законы одинаковы для всех инерциальных систем отсчета, независимо от их относительного состояния движения; и, во-вторых, скорость света в свободном пространстве одинакова во всех инерциальных системах отсчета, опять же, независимо от относительной скорости каждой системы отсчета. Преобразование Лоренца, по сути, является прямым следствием этого второго постулата.

Второй постулат

Предположим, что второй постулат специальной теории относительности, утверждающей постоянство скорости света, независимо от системы отсчета, и рассмотрим набор систем отсчета, движущихся относительно друг друга с постоянной скоростью, т. е. инерциальные системы, каждый наделен собственным набором Декартовы координаты маркировка точек, т.е. События пространства-времени. Чтобы выразить неизменность скорости света в математической форме, зафиксируйте два события в пространстве-времени, которые будут записаны в каждой системе отсчета. Пусть первым событием будет излучение светового сигнала, а вторым - его поглощение.

Выберите любую опорную рамку в коллекции. В его координатах первому событию будут присвоены координаты ${ displaystyle x_ {1}, y_ {1}, z_ {1}, ct_ {1}}$, а второй ${ displaystyle x_ {2}, y_ {2}, z_ {2}, ct_ {2}}$. Пространственное расстояние между излучением и поглощением равно ${ displaystyle { sqrt {(x_ {2} -x_ {1}) ^ {2} + (y_ {2} -y_ {1}) ^ {2} + (z_ {2} -z_ {1}) ^ {2}}}}$, но это тоже расстояние ${ displaystyle c (t_ {2} -t_ {1})}$ путешествовал по сигналу. Следовательно, можно составить уравнение

${ displaystyle c ^ {2} (t_ {2} -t_ {1}) ^ {2} - (x_ {2} -x_ {1}) ^ {2} - (y_ {2} -y_ {1} ) ^ {2} - (z_ {2} -z_ {1}) ^ {2} = 0.}$

Все остальные системы координат будут записывать то же уравнение в своих координатах. Это непосредственное математическое следствие неизменности скорости света. Величина слева называется пространственно-временной интервал. Интервал для событий, разделенных световыми сигналами, одинаков (ноль) во всех системах отсчета, и поэтому называется инвариантный.

Инвариантность интервала

Чтобы преобразование Лоренца имело физический смысл, осознаваемый природой, очень важно, чтобы интервал был инвариантной мерой для любой два события, а не только те, которые разделены световыми сигналами. Чтобы установить это, считается бесконечно малый интервал^[4]

${ displaystyle ds ^ {2} = c ^ {2} dt ^ {2} -dx ^ {2} -dy ^ {2} -dz ^ {2},}$

как записано в системе ${ displaystyle K}$. Позволять ${ displaystyle K '}$ быть другой системой, назначающей интервал ${ displaystyle ds '^ {2}}$ к одним и тем же двум бесконечно удаленным событиям. Поскольку если ${ displaystyle ds ^ {2} = 0}$, то интервал будет равен нулю в любой другой системе (второй постулат), и поскольку ${ displaystyle ds ^ {2}}$ и ${ displaystyle ds '^ {2}}$ бесконечно малы одного порядка, они должны быть пропорциональны друг другу,

${ displaystyle ds ^ {2} = ads '^ {2}.}$

На что может ${ displaystyle a}$ зависеть? Это может не зависеть от положения двух событий в пространстве-времени, потому что это нарушит постулируемый однородность пространства-времени. Это может зависеть от относительной скорости ${ displaystyle V '}$ между ${ displaystyle K}$ и ${ displaystyle K '}$, но только по скорости, а не по направлению, потому что последнее нарушит изотропия пространства.

Теперь внесите системы ${ displaystyle K_ {1}}$ и ${ displaystyle K_ {2}}$,

${ displaystyle ds ^ {2} = a (V_ {1}) ds_ {1} ^ {2}, quad ds ^ {2} = a (V_ {2}) ds_ {2} ^ {2}, quad ds_ {1} ^ {2} = a (V_ {12}) ds_ {2} ^ {2}.}$

Из этого следует,

${ displaystyle { frac {a (V_ {2})} {a (V_ {1})}} = a (V_ {12}).}$

Теперь можно заметить, что в правой части ${ displaystyle V_ {12}}$ зависеть от обоих ${ displaystyle V_ {1}}$ и ${ displaystyle V_ {2}}$; а также от угла между векторов ${ displaystyle { textbf {V}} _ {1}}$ и ${ displaystyle { textbf {V}} _ {2}}$. Однако можно также заметить, что левая часть не зависит от этого угла. Таким образом, единственный способ сохранить истинность уравнения - это если функция ${ Displaystyle а (V)}$ является константой. Далее, по тому же уравнению эта постоянная равна единице. Таким образом,

${ displaystyle ds ^ {2} = ds '^ {2}}$

для всех систем ${ displaystyle K '}$. Поскольку это верно для всех бесконечно малых интервалов, это верно для все интервалы.

Большинство, если не все, выводы преобразований Лоренца принимают это как должное [Неясно, что такое "это". "Это" то, что пространственно-временные интервалы равны? Или "это" то, что верно для всех бесконечно малых интервалов, также верно для все интервалы? ]. В этих выводах они используют только постоянство скорости света (инвариантность светоподобных отдельных событий). Этот результат гарантирует, что преобразование Лоренца является правильным преобразованием [опять же неясно, что означает «Это»].

Стандартная конфигурация

Пространственно-временные координаты события, измеренные каждым наблюдателем в своей инерциальной системе отсчета (в стандартной конфигурации), показаны в речевых пузырях.
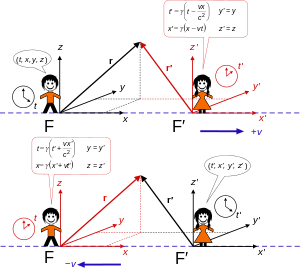
Верх: рамка F′ Движется со скоростью v вдоль Икс-ось рамы F.
Внизу: рамка F движется со скоростью -v вдоль Икс′ - ось рамы F′.^[5]

Инвариантный интервал можно рассматривать как функцию неположительно определенного расстояния в пространстве-времени. Набор искомых преобразований должен оставлять это расстояние неизменным. Из-за декартовой природы системы координат системы отсчета можно сделать вывод, что, как и в евклидовом случае, возможные преобразования состоят из сдвигов и вращений, при этом для термина «вращение» следует допускать несколько более широкое значение.

Интервал тривиально инвариантен относительно трансляции. Для поворотов есть четыре координаты. Следовательно, есть шесть плоскостей вращения. Три из них - это вращения в пространственных плоскостях. Интервал инвариантен и относительно обычных вращений.^[4]

Осталось найти «поворот» в трех оставшихся координатных плоскостях, при котором интервал остается неизменным. Точно так же найти способ назначить координаты, чтобы они совпадали с координатами, соответствующими движущейся системе отсчета.

Общая проблема состоит в том, чтобы найти такое преобразование, что

${ displaystyle { begin {align} & , , , , , , , , c ^ {2} (t_ {2} -t_ {1}) ^ {2} - (x_ { 2} -x_ {1}) ^ {2} - (y_ {2} -y_ {1}) ^ {2} - (z_ {2} -z_ {1}) ^ {2} & = c ^ {2} (t_ {2} '- t_ {1}') ^ {2} - (x_ {2} '- x_ {1}') ^ {2} - (y_ {2} '- y_ {1} ') ^ {2} - (z_ {2}' - z_ {1} ') ^ {2}. End {align}}}$

Для решения общей проблемы можно использовать знание об инвариантности интервала трансляций и обычных вращений, чтобы предположить, не ограничивая общности,^[4] что кадры F и F' выровнены таким образом, что их оси координат пересекаются в т = т' = 0 и что Икс и Икс' оси постоянно выровнены и система F' имеет скорость V вдоль положительного Икс-ось. Назовите это стандартная конфигурация. Это сводит общую проблему к нахождению такого преобразования, что

${ displaystyle c ^ {2} (t_ {2} -t_ {1}) ^ {2} - (x_ {2} -x_ {1}) ^ {2} = c ^ {2} (t_ {2} '-t_ {1}') ^ {2} - (x_ {2} '- x_ {1}') ^ {2}.}$

Стандартная конфигурация используется в большинстве примеров ниже. А линейный решение более простой проблемы

${ displaystyle c ^ {2} t ^ {2} -x ^ {2} = c ^ {2} t '^ {2} -x' ^ {2}}$

решает более общую проблему, поскольку координата различия затем трансформируйте таким же образом. При рассмотрении этой более простой проблемы в литературе часто предполагается или как-то аргументируется линейность. Если решение более простой проблемы нет linear, то он не решает исходную проблему из-за перекрестных членов, появляющихся при расширении квадратов.

Решения

Как уже упоминалось, общая проблема решается переводами в пространство-время. Они не кажутся решением более простой поставленной задачи, в отличие от бустов (а иногда и поворотов в зависимости от угла атаки). Еще больше решений существует, если один Только настаивают на неизменности интервала для светоподобных разделенных событий. Это нелинейные конформные («сохраняющие угол») преобразования. Надо

Преобразования Лоренца ⊂ Преобразования Пуанкаре ⊂ конформные групповые преобразования.

Некоторые уравнения физики конформно инвариантны, например то Уравнения Максвелла в пространстве без исходников,^[6] но не все. Актуальность конформных преобразований в пространстве-времени в настоящее время неизвестна, но конформная группа в двух измерениях очень важна в конформная теория поля и статистическая механика.^[7] Таким образом, именно группа Пуанкаре выделяется постулатами специальной теории относительности. Это наличие бустеров Лоренца (для которых сложение скорости отличается от простого сложения векторов, которое учитывает скорости, превышающие скорость света), в отличие от обычных ускорений, которые отделяют его от Галилейская группа из Галилея относительность. Пространственные вращения, пространственные и временные инверсии и трансляции присутствуют в обеих группах и имеют одинаковые последствия в обеих теориях (законы сохранения импульса, энергии и углового момента). Не все принятые теории соблюдают симметрию относительно инверсий.

Использование геометрии пространства-времени

Решение Ландау и Лифшица

Проблема поставлена ​​в стандартная конфигурация для повышения Икс-направление, где штрихованные координаты относятся к движущийся система решается путем нахождения линейный решение более простой проблемы

${ displaystyle c ^ {2} t ^ {2} -x ^ {2} = c ^ {2} t '^ {2} -x' ^ {2}.}$

Наиболее общее решение, как можно проверить прямой заменой с помощью (H1),^[4]

Чтобы найти роль Ψ в физических условиях зафиксируйте прогрессирование происхождения F', т.е. Икс' = 0, Икс = vt. Уравнения становятся (используя сначала Икс' = 0),

${ displaystyle x = ct ' sinh Psi, quad ct = ct' cosh Psi.}$

Теперь разделите:

${ displaystyle { frac {x} {ct}} = tanh Psi = { frac {v} {c}} Rightarrow quad sinh Psi = { frac { frac {v} {c} } { sqrt {1 - { frac {v ^ {2}} {c ^ {2}}}}}}, quad cosh Psi = { frac {1} { sqrt {1 - { гидроразрыв {v ^ {2}} {c ^ {2}}}}}},}$

куда Икс = vt использовался на первом этапе, (H2) и (H3) на втором, которые при повторном подключении (1), дает

${ displaystyle x = { frac {x '+ vt'} { sqrt {1 - { frac {v ^ {2}} {c ^ {2}}}}}}, quad t = { frac {t '+ { frac {v} {c ^ {2}}} x'} { sqrt {1 - { frac {v ^ {2}} {c ^ {2}}}}}},}$

или, используя обычные сокращения,

Этот расчет повторяется более подробно в разделе гиперболическое вращение.

Гиперболическое вращение

Преобразования Лоренца также могут быть получены простым применением постулаты специальной теории относительности и используя гиперболические тождества.^[8]

Постулаты относительности

Начнем с уравнений сферического волнового фронта светового импульса с центром в начале координат:

${ displaystyle (ct) ^ {2} - (x ^ {2} + y ^ {2} + z ^ {2}) = (ct ') ^ {2} - (x' ^ {2} + y ' ^ {2} + z '^ {2}) = 0}$

которые принимают одинаковую форму в обеих системах отсчета из-за постулатов специальной теории относительности. Затем рассмотрим относительное движение по Икс- оси каждого кадра в стандартной конфигурации, указанной выше, так что y = y′, z = z′, Что упрощает

${ displaystyle (ct) ^ {2} -x ^ {2} = (ct ') ^ {2} -x' ^ {2}}$

Линейность

Теперь предположим, что преобразования принимают линейный вид:

${ displaystyle { begin {align} x '& = Ax + Bct ct' & = Cx + Dct end {align}}}$

куда А, B, C, D должны быть найдены. Если бы они были нелинейными, они не принимали бы одинаковую форму для всех наблюдателей, поскольку фиктивные силы (следовательно, ускорения) происходили бы в одном кадре, даже если бы скорость была постоянной в другом, что несовместимо с преобразованиями инерциального кадра.^[9]

Подставляем в предыдущий результат:

${ displaystyle (ct) ^ {2} -x ^ {2} = [(Cx) ^ {2} + (Dct) ^ {2} + 2CDcxt] - [(Ax) ^ {2} + (Bct) ^ {2} + 2ABcxt]}$

и сравнивая коэффициенты Икс², т², xt:

${ displaystyle { begin {align} -1 = C ^ {2} -A ^ {2} & Rightarrow & A ^ {2} -C ^ {2} = 1 c ^ {2} = (Dc) ^ {2} - (Bc) ^ {2} & Rightarrow & D ^ {2} -B ^ {2} = 1 2CDc-2ABc = 0 & Rightarrow & AB = CD end {выровнено}}}$

Гиперболическое вращение

Уравнения предполагают гиперболическое тождество ${ displaystyle cosh ^ {2} phi - sinh ^ {2} phi = 1.}$

Представляем быстрота параметр ϕ как гиперболический угол позволяет последовательную идентификацию

${ Displaystyle А = D = сш фи ,, квад С = В = - зп фи}$

где знаки после квадратных корней выбраны так, чтобы Икс и т увеличивать. Гиперболические преобразования решены для:

${ displaystyle { begin {align} x '& = x cosh phi -ct sinh phi ct' & = - x sinh phi + ct cosh phi end {align}}}$

Если бы знаки были выбраны иначе, координаты положения и времени необходимо было бы заменить на -Икс и / или -т так что Икс и т увеличение, а не уменьшение.

Чтобы узнать, как ϕ относится к относительной скорости, из стандартной конфигурации начало заправленной рамки Икс′ = 0 измеряется в незаштрихованном кадре как Икс = vt (или эквивалентным и противоположным способом; начало кадра без штриха Икс = 0, а в штрихованном кадре - на Икс′ = −vt):

${ displaystyle 0 = vt cosh phi -ct sinh phi , Rightarrow , tanh phi = { frac {v} {c}} = beta}$

и манипулирование гиперболическими тождествами приводит к отношениям между β, γ, и ϕ,

${ Displaystyle сш фи = гамма, , квад зп фи = бета гамма ,.}$

Из физических принципов

Проблема обычно ограничивается двумя измерениями за счет использования скорости вдоль Икс ось такая, что y и z координаты не вмешиваются, как описано в стандартная конфигурация над.

Замедление времени и сокращение длины

Уравнения преобразования могут быть получены из замедление времени и сокращение длины, которые, в свою очередь, могут быть выведены из первых принципов. С О и O ′ представляя пространственное происхождение кадров F и F ′, и какое-то событие M, связь между векторами позиций (которые здесь сводятся к ориентированным сегментам ОМ, OO ′ и О'М) в обоих кадрах определяется выражением:^[10]

ОМ = OO ′ + О'М.

Используя координаты (х, т) в F и (х ′, t ′) в F ′ для события M, в кадре F сегменты ОМ = Икс, OO ′ = vt и О'М = Икс'/γ (поскольку Икс' является О'М как измерено в F ′):

${ displaystyle x = vt + x '/ gamma.}$

Точно так же в кадре F ′, сегменты ОМ = Икс/γ (поскольку Икс является ОМ как измерено в F), OO ′ = vt ′ и О'М = Икс':

${ displaystyle x / gamma = vt '+ x'.}$

Преобразуя первое уравнение, получаем

${ Displaystyle х '= гамма (х-vt),}$

что является пространственной частью преобразования Лоренца. Второе соотношение дает

${ Displaystyle х = гамма (х '+ vt'),}$

что является инверсией космической части. Устранение Икс' между двумя уравнениями пространственной части дает

${ Displaystyle т '= гамма (т-vx / с ^ {2}),}$

что является временной частью преобразования, обратное к которому находится аналогичным удалением Икс:

${ displaystyle t = gamma (t '+ vx' / c ^ {2}).}$

Сферические световые фронты

Следующее похоже на Эйнштейна.^[11][12]Как в Преобразование Галилея преобразование Лоренца является линейным, поскольку относительная скорость систем отсчета постоянна как вектор; иначе, инерционные силы представляется. Их называют инерциальными или галилеевыми системами отсчета. Согласно теории относительности никакая система отсчета Галилея не является привилегированной. Другое условие состоит в том, что скорость света не должна зависеть от системы отсчета, на практике от скорости источника света.

Рассмотрим два инерциальные системы отсчета О и О′, Предполагая О быть в покое пока О′ Движется со скоростью v относительно О в положительном Икс-направление. Истоки О и О′ Изначально совпадают друг с другом. Световой сигнал исходит из общего источника и распространяется как сферический волновой фронт. Рассмотрим точку п на сферическом волновой фронт На расстоянии р и р′ От истоков О и О' соответственно. Согласно второму постулату специальная теория относительности то скорость света одинаково в обоих кадрах, поэтому для точки п:

${ Displaystyle { begin {выровнено} r & = ct r '& = ct'. end {выравнивается}}}$

Уравнение шара в кадре О дан кем-то

${ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = r ^ {2}.}$

Для сферической волновой фронт это становится

${ displaystyle x ^ {2} + y ^ {2} + z ^ {2} = c ^ {2} t ^ {2}.}$

Аналогично уравнение сферы в системе отсчета О' дан кем-то

${ displaystyle x '^ {2} + y' ^ {2} + z '^ {2} = r' ^ {2},}$

так сферический волновой фронт удовлетворяет

${ displaystyle x '^ {2} + y' ^ {2} + z '^ {2} = c ^ {2} t' ^ {2}.}$

Происхождение О'Движется Икс-ось. Следовательно,

${ displaystyle { begin {align} y '& = y z' & = z. end {align}}}$

Икс′ Должен линейно изменяться с Икс и т. Следовательно, преобразование имеет вид

${ Displaystyle х '= гамма х + сигма т.}$

За происхождение О′ Икс' и Икс даны

${ displaystyle { begin {align} x '& = 0 x & = vt, end {align}}}$

так, для всех т,

${ displaystyle 0 = gamma vt + sigma t}$

и поэтому

${ Displaystyle sigma = - gamma v.}$

Это упрощает преобразование в

${ Displaystyle х '= гамма влево (х-vt вправо)}$

где γ подлежит определению. В этой точке γ не обязательно является константой, но необходимо уменьшить до 1 для v ≪ c.

Обратное преобразование такое же, за исключением того, что знак v обратный:

${ displaystyle x = gamma left (x '+ vt' right).}$

Два приведенных выше уравнения дают связь между т и т' в качестве:

${ Displaystyle х = гамма влево [ гамма влево (х-vt вправо) + vt ' вправо]}$

или же

${ displaystyle t '= gamma t + { frac { left (1 - { gamma ^ {2}} right) x} { gamma v}}.}$

Замена Икс′, y′, z' и т′ В сферической волновой фронт уравнение в О' Рамка,

${ displaystyle x '^ {2} + y' ^ {2} + z '^ {2} = c ^ {2} t' ^ {2},}$

с их выражениями в терминах Икс, y, z и т производит:

${ displaystyle { gamma ^ {2}} left (x-vt right) ^ {2} + y ^ {2} + z ^ {2} = c ^ {2} left [ gamma t + { frac { left (1 - { gamma ^ {2}} right) x} { gamma v}} right] ^ {2}}$

и поэтому,

${ displaystyle gamma ^ {2} x ^ {2} + gamma ^ {2} v ^ {2} t ^ {2} -2 gamma ^ {2} vtx + y ^ {2} + z ^ { 2} = c ^ {2} { gamma ^ {2}} t ^ {2} + { frac { left (1 - { gamma ^ {2}} right) ^ {2} c ^ {2 } x ^ {2}} {{ gamma ^ {2}} v ^ {2}}} + 2 { frac { left (1 - { gamma ^ {2}} right) txc ^ {2} } {v}}}$

что означает,

${ displaystyle left [{ gamma ^ {2}} - { frac { left (1 - { gamma ^ {2}} right) ^ {2} c ^ {2}} {{ gamma ^ {2}} v ^ {2}}} right] x ^ {2} -2 { gamma ^ {2}} vtx + y ^ {2} + z ^ {2} = left (c ^ {2 } { gamma ^ {2}} - v ^ {2} { gamma ^ {2}} right) t ^ {2} +2 { frac { left [1 - { gamma ^ {2}} right] txc ^ {2}} {v}}}$

или же

${ displaystyle left [{ gamma ^ {2}} - { frac { left (1 - { gamma ^ {2}} right) ^ {2} c ^ {2}} {{ gamma ^ {2}} v ^ {2}}} right] x ^ {2} - left [2 { gamma ^ {2}} v + 2 { frac { left (1 - { gamma ^ {2 }} right) c ^ {2}} {v}} right] tx + y ^ {2} + z ^ {2} = left [c ^ {2} { gamma ^ {2}} - v ^ {2} { gamma ^ {2}} right] t ^ {2}}$

Сравнивая коэффициент т² в приведенном выше уравнении с коэффициентом т² в сферическом волновой фронт уравнение для рамы О производит:

${ displaystyle c ^ {2} { gamma ^ {2}} - v ^ {2} { gamma ^ {2}} = c ^ {2}}$

Эквивалентные выражения для γ могут быть получены путем сопоставления Икс² коэффициенты или установка tx коэффициент к нулю. Перестановка:

${ displaystyle { gamma ^ {2}} = { frac {1} {1 - { frac {v ^ {2}} {c ^ {2}}}}}}$

или, выбирая положительный корень, чтобы гарантировать, что оси x и x 'и оси времени указывают в одном направлении,

${ displaystyle { gamma} = { frac {1} { sqrt {1 - { frac {v ^ {2}} {c ^ {2}}}}}}}$

который называется Фактор Лоренца. Это производит Преобразование Лоренца из приведенного выше выражения. Это дается

${ displaystyle { begin {align} x '& = gamma left (x-vt right) t' & = gamma left (t - { frac {vx} {c ^ {2}} } right) y '& = y z' & = z end {align}}}$

Преобразование Лоренца - не единственное преобразование, оставляющее неизменной форму сферических волн, поскольку существует более широкий набор преобразования сферических волн в контексте конформная геометрия, оставляя неизменным выражение ${ displaystyle lambda left ( delta x ^ {2} + delta y ^ {2} + delta z ^ {2} -c ^ {2} delta t ^ {2} right)}$. Однако конформные преобразования, изменяющие масштаб, нельзя использовать для симметричного описания всех законов природы, включая механика, тогда как преобразования Лоренца (единственное, что подразумевает ${ displaystyle lambda = 1}$) представляют собой симметрию всех законов природы и сводятся к преобразованиям Галилея при ${ displaystyle v ll c}$.

Теория относительности Галилея и Эйнштейна

Галилеевы системы отсчета

В классической кинематике полное перемещение Икс в рамке R - это сумма относительного смещения Икс′ В системе отсчета R ′ и расстояния между двумя исходными точками Икс − Икс′. Если v - относительная скорость R ′ относительно R, преобразование: Икс = Икс′ + vt, или же Икс′ = Икс − vt. Эта зависимость линейна для постоянного v, вот когда р и р′ Являются галилеевскими системами отсчета.

Главное отличие теории относительности Эйнштейна от теории относительности Галилея состоит в том, что координаты пространства и времени взаимосвязаны и находятся в разных инерциальных системах отсчета. т ≠ т′.

Поскольку пространство предполагается однородным, преобразование должно быть линейным. Наиболее общая линейная зависимость получается с четырьмя постоянными коэффициентами, А, B, γ и б:

${ Displaystyle х '= гамма х + bt ,}$

${ displaystyle t '= Ax + Bt. ,}$

Преобразование Лоренца становится преобразованием Галилея, когда γ = B = 1, б = −v и А = 0.

Покоящийся объект в рамке R ′ в позиции Икс′ = 0 движется с постоянной скоростью v в кадре R. Следовательно, преобразование должно дать Икс′ = 0, если Икс = vt. Следовательно, б = −γv а первое уравнение записывается как

${ Displaystyle х '= гамма (х-vt) ,.}$

Используя принцип относительности

Согласно принципу относительности, привилегированной системы отсчета Галилея не существует: поэтому обратное преобразование для положения из системы отсчета р' к кадру р должен иметь ту же форму, что и оригинал, но со скоростью в противоположном направлении, т.е. замена v с -v:

${ Displaystyle х = гамма влево (х '- (- v) т' вправо),}$

и поэтому

${ displaystyle x = gamma left (x '+ vt' right).}$

Определение постоянных первого уравнения

Поскольку скорость света одинакова во всех системах отсчета, в случае светового сигнала преобразование должно гарантировать, что т = Икс/c когда т′ = Икс′/c.

Замена на т и т′ В предыдущих уравнениях дает:

${ Displaystyle х '= гамма влево (1-v / с вправо) х,}$

${ displaystyle x = gamma left (1 + v / c right) x '.}$

Умножение этих двух уравнений вместе дает,

${ displaystyle xx '= gamma ^ {2} left (1-v ^ {2} / c ^ {2} right) xx'.}$

В любое время после т = т′ = 0, хх′ Не равно нулю, поэтому разделив обе части уравнения на хх'Приводит к

${ displaystyle gamma = { frac {1} { sqrt {1 - { frac {v ^ {2}} {c ^ {2}}}}}},}$

который называется «фактором Лоренца».

Когда требуется, чтобы уравнения преобразования удовлетворяли уравнениям светового сигнала в виде Икс = ct и Икс′ = ct', Подставляя значения x и x', тот же метод дает такое же выражение для фактора Лоренца.^[13][14]

Определение постоянных второго уравнения

Уравнение преобразования для времени можно легко получить, рассмотрев частный случай светового сигнала, снова удовлетворяющий Икс = ct и Икс′ = ct′, Подставляя член за членом ранее полученное уравнение для пространственной координаты

${ Displaystyle х '= гамма (х-vt), ,}$

давая

${ displaystyle ct '= gamma left (ct - { frac {v} {c}} x right),}$

так что

${ displaystyle t '= gamma left (t - { frac {v} {c ^ {2}}} x right),}$

который при отождествлении с

${ displaystyle t '= Ax + Bt, ,}$

определяет коэффициенты преобразования А и B в качестве

${ Displaystyle А = - гамма v / с ^ {2}, ,}$

${ Displaystyle В = гамма. ,}$

Так А и B являются уникальными постоянными коэффициентами, необходимыми для сохранения постоянства скорости света в системе координат со штрихом.

Популярный вывод Эйнштейна

В своей популярной книге^[15] Эйнштейн вывел преобразование Лоренца, утверждая, что должны быть две ненулевые константы связи λ и μ такой, что

${ displaystyle { begin {case} x'-ct '= lambda left (x-ct right) x' + ct '= mu left (x + ct right) , end { случаи}}}$

которые соответствуют движению света вдоль положительной и отрицательной оси абсцисс соответственно. Икс = ct если и только если Икс′ = ct′. Сложение и вычитание двух уравнений и определение

${ Displaystyle { begin {case} gamma = left ( lambda + mu right) / 2 b = left ( lambda - mu right) / 2, , end {cases} }}$

дает

${ Displaystyle { begin {case} x '= gamma x-bct ct' = gamma ct-bx. , end {cases}}}$

Подстановка Икс′ = 0 соответствующий Икс = vt и отмечая, что относительная скорость v = до н.э/γ, это дает

${ displaystyle { begin {case} x '= gamma left (x-vt right) t' = gamma left (t - { frac {v} {c ^ {2}}} x right) , end {case}}}$

Постоянная γ можно оценить, потребовав c²т² − Икс² = c²т'² − Икс'² согласно стандартная конфигурация.

Используя теорию групп

Из групповых постулатов

Ниже приводится классический вывод (см., Например, [1] и ссылки там), основанные на групповых постулатах и ​​изотропии пространства.

Координатные преобразования как группа

Преобразования координат между инерциальными системами отсчета образуют группа (называется собственно группа Лоренца ), причем групповая операция представляет собой композицию преобразований (выполнение одного преобразования за другим). Действительно, четыре групповых аксиомы выполнены:

1. Закрытие: композиция двух преобразований является преобразованием: рассмотрим композицию преобразований из инерциальной системы отсчета K к инерциальной системе отсчета K′, (Обозначается как K → K′), А затем из K′ В инерциальную систему отсчета K′′, [K′ → K′ ′], Существует преобразование [K → K′] [K′ → K′ ′], Непосредственно из инерциальной системы отсчета K к инерциальной системе отсчета K′′.
2. Ассоциативность: преобразования ([K → K′] [K′ → K′′] ) [K′′ → K'''] и [K → K′] ( [K′ → K′′] [K′′ → K′ ′ ′]) Идентичны.
3. Элемент идентичности: есть элемент идентичности, трансформация K → K.
4. Обратный элемент: для любого преобразования K → K′ Существует обратное преобразование K′ → K.

Матрицы преобразований в соответствии с аксиомами групп

Рассмотрим две инерциальные системы отсчета, K и K′, Последний движется со скоростью v по отношению к первому. Путем поворота и сдвига мы можем выбрать Икс и Икс′ Вдоль вектора относительной скорости, а также что события (т, Икс)=(0,0) и (т′, Икс′)=(0,0) совпадают. Поскольку увеличение скорости происходит по Икс (и Икс′) оси ничего не происходит с перпендикулярными координатами, и мы можем просто опустить их для краткости. Теперь, поскольку преобразование, которое мы ищем, соединяет две инерциальные системы отсчета, оно должно преобразовать линейное движение в (т, Икс) в поступательное движение в (т′, Икс′) координаты. Следовательно, это должно быть линейное преобразование. Общий вид линейного преобразования:

${ displaystyle { begin {bmatrix} t ' x' end {bmatrix}} = { begin {bmatrix} gamma & delta beta & alpha end {bmatrix}} { begin { bmatrix} t x end {bmatrix}},}$

куда α, β, γ и δ некоторые еще неизвестные функции относительной скорости v.

Рассмотрим теперь движение начала отсчета K′. в K'Кадр имеет координаты (т′, Икс′=0), а в K рамка имеет координаты (т, Икс=vt). Эти две точки связаны преобразованием

${ displaystyle { begin {bmatrix} t ' 0 end {bmatrix}} = { begin {bmatrix} gamma & delta beta & alpha end {bmatrix}} { begin {bmatrix} } t vt end {bmatrix}},}$

откуда мы получаем

${ Displaystyle бета = -v альфа ,}$.

Аналогично, учитывая движение начала отсчета K, мы получили

${ displaystyle { begin {bmatrix} t ' - vt' end {bmatrix}} = { begin {bmatrix} gamma & delta beta & alpha end {bmatrix}} { begin {bmatrix} t 0 end {bmatrix}},}$

откуда мы получаем

${ Displaystyle бета = -v гамма ,}$.

Объединение этих двух дает α = γ и матрица преобразования упростилась,

${ displaystyle { begin {bmatrix} t ' x' end {bmatrix}} = { begin {bmatrix} gamma & delta - v gamma & gamma end {bmatrix}} { begin {bmatrix} t x end {bmatrix}}.}$

Теперь рассмотрим групповой постулат обратный элемент. Есть два способа выйти из K′ Системы координат к K система координат. Во-первых, применить обратную матрицу преобразования к KКоординаты:

${ displaystyle { begin {bmatrix} t x end {bmatrix}} = { frac {1} { gamma ^ {2} + v delta gamma}} { begin {bmatrix} gamma & - delta v gamma & gamma end {bmatrix}} { begin {bmatrix} t ' x' end {bmatrix}}.}$

Во-вторых, учитывая, что K′ Система координат движется со скоростью v относительно K система координат, K система координат должна двигаться со скоростью -v относительно K' система координат. Замена v с -v в матрице преобразования дает:

${ displaystyle { begin {bmatrix} t x end {bmatrix}} = { begin {bmatrix} gamma (-v) & delta (-v) v gamma (-v) & гамма (-v) end {bmatrix}} { begin {bmatrix} t ' x' end {bmatrix}},}$

Теперь функция γ не может зависеть от направления v потому что это, по-видимому, фактор, определяющий релятивистское сжатие и замедление времени. Эти двое (в нашем изотропном мире) не могут зависеть от направления v. Таким образом, γ(-v) = γ(v) и сравнивая две матрицы, получаем

${ Displaystyle гамма ^ {2} + v дельта гамма = 1. ,}$

Согласно закрытие Постулат группы: композиция двух преобразований координат также является преобразованием координат, поэтому произведение двух наших матриц также должно быть матрицей той же формы. Преобразование K к K' и из K' к K′ ′ Дает следующую матрицу преобразования для перехода от K к K′′:

${ displaystyle { begin {align} { begin {bmatrix} t '' x '' end {bmatrix}} & = { begin {bmatrix} gamma (v ') & delta (v') - v ' gamma (v') & gamma (v ') end {bmatrix}} { begin {bmatrix} gamma (v) & delta (v) - v gamma (v) & gamma (v) end {bmatrix}} { begin {bmatrix} t x end {bmatrix}} & = { begin {bmatrix} gamma (v ') gamma (v) - v delta (v ') gamma (v) & gamma (v') delta (v) + delta (v ') gamma (v) - (v' + v) gamma (v ' ) gamma (v) & - v ' gamma (v') delta (v) + gamma (v ') gamma (v) end {bmatrix}} { begin {bmatrix} t x конец {bmatrix}}. end {выравнивается}}}$

В исходной матрице преобразования оба основных диагональных элемента равны γ, следовательно, чтобы комбинированная матрица преобразования, приведенная выше, имела ту же форму, что и исходная матрица преобразования, основные диагональные элементы также должны быть равны. Приравнивание этих элементов и перестановка дает:

${ Displaystyle гамма (v ') гамма (v) -v delta (v') gamma (v) = - v ' gamma (v') delta (v) + gamma (v ') гамма (v) ,}$

${ Displaystyle v дельта (v ') гамма (v) = v' гамма (v ') delta (v) ,}$

${ displaystyle { frac { delta (v)} {v gamma (v)}} = { frac { delta (v ')} {v' gamma (v ')}}. ,}$

Знаменатель будет отличным от нуля при ненулевом v, потому что γ(v) всегда отличен от нуля;

${ displaystyle gamma ^ {2} + v delta gamma = 1}$.

Если v=0 у нас есть единичная матрица, которая совпадает с положением v=0 in the matrix we get at the end of this derivation for the other values of v, making the final matrix valid for all nonnegative v.

For the nonzero v, this combination of function must be a universal constant, one and the same for all inertial frames. Define this constant as δ(v)/v γ(v)= κ, куда κ имеет измерение из 1/v². Решение

${displaystyle 1=gamma ^{2}+vdelta gamma =gamma ^{2}(1+kappa v^{2}),}$

we finally get

${displaystyle gamma =1/{sqrt {1+kappa v^{2}}}}$

and thus the transformation matrix, consistent with the group axioms, is given by

${displaystyle {egin{bmatrix}t'x'end{bmatrix}}={frac {1}{sqrt {1+kappa v^{2}}}}{egin{bmatrix}1&kappa v-v&1end{bmatrix}}{egin{bmatrix}txend{bmatrix}}.}$

Если κ > 0, then there would be transformations (with κv² ≫1) which transform time into a spatial coordinate and vice versa. We exclude this on physical grounds, because time can only run in the positive direction. Thus two types of transformation matrices are consistent with group postulates:

Galilean transformations

Если κ = 0 then we get the Galilean-Newtonian kinematics with the Galilean transformation,

${displaystyle {egin{bmatrix}t'x'end{bmatrix}}={egin{bmatrix}1&0-v&1end{bmatrix}}{egin{bmatrix}txend{bmatrix}};,}$

where time is absolute, т′=t, and the relative velocity v of two inertial frames is not limited.

Преобразования Лоренца

Если κ < 0, then we set ${displaystyle c=1/{sqrt {-kappa }}}$ который становится invariant speed, то скорость света в вакууме. Это дает κ = -1/c² and thus we get special relativity with Lorentz transformation

${displaystyle {egin{bmatrix}t'x'end{bmatrix}}={frac {1}{sqrt {1-{v^{2} over c^{2}}}}}{egin{bmatrix}1&{-v over c^{2}}-v&1end{bmatrix}}{egin{bmatrix}txend{bmatrix}};,}$

where the speed of light is a finite universal constant determining the highest possible relative velocity between inertial frames.

Если v ≪ c the Galilean transformation is a good approximation to the Lorentz transformation.

Only experiment can answer the question which of the two possibilities, κ = 0 или же κ < 0, is realised in our world. The experiments measuring the speed of light, first performed by a Danish physicist Оле Рёмер, show that it is finite, and the Michelson–Morley experiment showed that it is an absolute speed, and thus that κ < 0.

Boost from generators

Using rapidity ϕ to parametrize the Lorentz transformation, the boost in the Икс direction is

${displaystyle {egin{bmatrix}ct'x'y'z'end{bmatrix}}={egin{bmatrix}cosh phi &-sinh phi &0&0-sinh phi &cosh phi &0&0�&0&1&0�&0&0&1end{bmatrix}}{egin{bmatrix}c,txyzend{bmatrix}},}$

likewise for a boost in the y-направление

${displaystyle {egin{bmatrix}ct'x'y'z'end{bmatrix}}={egin{bmatrix}cosh phi &0&-sinh phi &0�&1&0&0-sinh phi &0&cosh phi &0�&0&0&1end{bmatrix}}{egin{bmatrix}c,txyzend{bmatrix}},}$

и z-направление

${displaystyle {egin{bmatrix}ct'x'y'z'end{bmatrix}}={egin{bmatrix}cosh phi &0&0&-sinh phi �&1&0&0�&0&1&0-sinh phi &0&0&cosh phi end{bmatrix}}{egin{bmatrix}c,txyzend{bmatrix}},.}$

куда е_Икс, е_y, е_z являются Cartesian basis vectors, a set of mutually perpendicular unit vectors along their indicated directions. If one frame is boosted with velocity v relative to another, it is convenient to introduce a единичный вектор п = v/v = β/β in the direction of relative motion. The general boost is

${displaystyle {egin{bmatrix}c,t'x'y'z'end{bmatrix}}={egin{bmatrix}cosh phi &-n_{x}sinh phi &-n_{y}sinh phi &-n_{z}sinh phi -n_{x}sinh phi &1+(cosh phi -1)n_{x}^{2}&(cosh phi -1)n_{x}n_{y}&(cosh phi -1)n_{x}n_{z}-n_{y}sinh phi &(cosh phi -1)n_{y}n_{x}&1+(cosh phi -1)n_{y}^{2}&(cosh phi -1)n_{y}n_{z}-n_{z}sinh phi &(cosh phi -1)n_{z}n_{x}&(cosh phi -1)n_{z}n_{y}&1+(cosh phi -1)n_{z}^{2}end{bmatrix}}{egin{bmatrix}c,txyzend{bmatrix}},.}$

Notice the matrix depends on the direction of the relative motion as well as the rapidity, in all three numbers (two for direction, one for rapidity).

We can cast each of the boost matrices in another form as follows. First consider the boost in the Икс направление. В Расширение Тейлора of the boost matrix about ϕ = 0 является

${displaystyle B(mathbf {e} _{x},phi )=sum _{n=0}^{infty }{frac {phi ^{n}}{n!}}left.{frac {partial ^{n}B(mathbf {e} _{x},phi )}{partial phi ^{n}}} ight|_{phi =0}}$

where the derivatives of the matrix with respect to ϕ are given by differentiating each entry of the matrix separately, and the notation |_{ϕ = 0} указывает ϕ is set to zero после the derivatives are evaluated. Expanding to first order gives the бесконечно малый трансформация

${displaystyle B(mathbf {e} _{x},phi )=I+phi left.{frac {partial B}{partial phi }} ight|_{phi =0}={egin{bmatrix}1&0&0&0�&1&0&0�&0&1&0�&0&0&1end{bmatrix}}-phi {egin{bmatrix}0&1&0&01&0&0&0�&0&0&0�&0&0&0end{bmatrix}}}$

which is valid if ϕ is small (hence ϕ² and higher powers are negligible), and can be interpreted as no boost (the first term я is the 4×4 identity matrix), followed by a small boost. Матрица

${displaystyle K_{x}={egin{bmatrix}0&1&0&01&0&0&0�&0&0&0�&0&0&0end{bmatrix}}}$

это генератор of the boost in the Икс direction, so the infinitesimal boost is

${displaystyle B(mathbf {e} _{x},phi )=I-phi K_{x}}$

Сейчас же, ϕ is small, so dividing by a positive integer N gives an even smaller increment of rapidity ϕ/N, и N of these infinitesimal boosts will give the original infinitesimal boost with rapidity ϕ,

${displaystyle B(mathbf {e} _{x},phi )=left(I-{frac {phi K_{x}}{N}} ight)^{N}}$

In the limit of an infinite number of infinitely small steps, we obtain the finite boost transformation

${displaystyle B(mathbf {e} _{x},phi )=lim _{N ightarrow infty }left(I-{frac {phi K_{x}}{N}} ight)^{N}=e^{-phi K_{x}}}$

which is the limit definition of the exponential из-за Леонард Эйлер, and is now true for any ϕ.

Repeating the process for the boosts in the y и z directions obtains the other generators

${displaystyle K_{y}={egin{bmatrix}0&0&1&0�&0&0&01&0&0&0�&0&0&0end{bmatrix}},,quad K_{z}={egin{bmatrix}0&0&0&1�&0&0&0�&0&0&01&0&0&0end{bmatrix}}}$

and the boosts are

${displaystyle B(mathbf {e} _{y},phi )=e^{-phi K_{y}},,quad B(mathbf {e} _{z},phi )=e^{-phi K_{z}},.}$

For any direction, the infinitesimal transformation is (small ϕ and expansion to first order)

${displaystyle B(mathbf {n} ,phi )=I+phi left.{frac {partial B}{partial phi }} ight|_{phi =0}={egin{bmatrix}1&0&0&0�&1&0&0�&0&1&0�&0&0&1end{bmatrix}}-phi {egin{bmatrix}0&n_{x}&n_{y}&n_{z} _{x}&0&0&0 _{y}&0&0&0 _{z}&0&0&0end{bmatrix}}}$

куда

${displaystyle {egin{bmatrix}0&n_{x}&n_{y}&n_{z} _{x}&0&0&0 _{y}&0&0&0 _{z}&0&0&0end{bmatrix}}=n_{x}K_{x}+n_{y}K_{y}+n_{z}K_{z}=mathbf {n} cdot mathbf {K} }$

is the generator of the boost in direction п. It is the full boost generator, a vector of matrices K = (K_Икс, K_y, K_z), projected into the direction of the boost п. The infinitesimal boost is

${displaystyle B(mathbf {n} ,phi )=I-phi (mathbf {n} cdot mathbf {K} )}$

Then in the limit of an infinite number of infinitely small steps, we obtain the finite boost transformation

${displaystyle B(mathbf {n} ,phi )=lim _{N ightarrow infty }left(I-{frac {phi (mathbf {n} cdot mathbf {K} )}{N}} ight)^{N}=e^{-phi (mathbf {n} cdot mathbf {K} )}}$

which is now true for any ϕ. Расширение matrix exponential из −ϕ(п · K) in its power series

${displaystyle e^{-phi mathbf {n} cdot mathbf {K} }=sum _{n=0}^{infty }{frac {1}{n!}}(-phi mathbf {n} cdot mathbf {K} )^{n}}$

we now need the powers of the generator. The square is

${displaystyle (mathbf {n} cdot mathbf {K} )^{2}={egin{bmatrix}1&0&0&0�&n_{x}^{2}&n_{x}n_{y}&n_{x}n_{z}�&n_{y}n_{x}&n_{y}^{2}&n_{y}n_{z}�&n_{z}n_{x}&n_{z}n_{y}&n_{z}^{2}end{bmatrix}}}$

but the cube (п · K)³ возвращается к (п · K), and as always the zeroth power is the 4×4 identity, (п · K)⁰ = я. In general the odd powers п = 1, 3, 5, ... находятся

${displaystyle (mathbf {n} cdot mathbf {K} )^{n}=(mathbf {n} cdot mathbf {K} )}$

while the even powers п = 2, 4, 6, ... находятся

${displaystyle (mathbf {n} cdot mathbf {K} )^{n}=(mathbf {n} cdot mathbf {K} )^{2}}$

therefore the explicit form of the boost matrix depends only the generator and its square. Splitting the power series into an odd power series and an even power series, using the odd and even powers of the generator, and the Taylor series of грехϕ и шишϕ о ϕ = 0 obtains a more compact but detailed form of the boost matrix

${displaystyle {egin{aligned}e^{-phi mathbf {n} cdot mathbf {K} }&=-sum _{n=1,3,5ldots }^{infty }{frac {1}{n!}}phi ^{n}(mathbf {n} cdot mathbf {K} )^{n}+sum _{n=0,2,4ldots }^{infty }{frac {1}{n!}}phi ^{n}(mathbf {n} cdot mathbf {K} )^{n}&=-left[phi +{frac {phi ^{3}}{3!}}+{frac {phi ^{5}}{5!}}+cdots ight](mathbf {n} cdot mathbf {K} )+I+left[-1+1+{frac {1}{2!}}phi ^{2}+{frac {1}{4!}}phi ^{4}+{frac {1}{6!}}phi ^{6}+cdots ight](mathbf {n} cdot mathbf {K} )^{2}&=-sinh phi (mathbf {n} cdot mathbf {K} )+I+(-1+cosh phi )(mathbf {n} cdot mathbf {K} )^{2}end{aligned}}}$

куда 0 = − 1 + 1 is introduced for the even power series to complete the Taylor series for шишϕ. The boost is similar to Rodrigues' rotation formula,

${displaystyle B(mathbf {n} ,phi )=e^{-phi mathbf {n} cdot mathbf {K} }=I-sinh phi (mathbf {n} cdot mathbf {K} )+(cosh phi -1)(mathbf {n} cdot mathbf {K} )^{2},.}$

Negating the rapidity in the exponential gives the inverse transformation matrix,

${displaystyle B(mathbf {n} ,-phi )=e^{phi mathbf {n} cdot mathbf {K} }=I+sinh phi (mathbf {n} cdot mathbf {K} )+(cosh phi -1)(mathbf {n} cdot mathbf {K} )^{2},.}$

В квантовая механика, релятивистская квантовая механика, и квантовая теория поля, a different convention is used for the boost generators; all of the boost generators are multiplied by a factor of the imaginary unit я = √−1.

From experiments

Howard Percy Robertson and others showed that the Lorentz transformation can also be derived empirically.^[16][17] In order to achieve this, it's necessary to write down coordinate transformations that include experimentally testable parameters. For instance, let there be given a single "preferred" inertial frame ${displaystyle X,Y,Z,T}$ in which the speed of light is constant, isotropic, and independent of the velocity of the source. It is also assumed that Einstein synchronization and synchronization by slow clock transport are equivalent in this frame. Then assume another frame ${displaystyle x,y,z,t}$ in relative motion, in which clocks and rods have the same internal constitution as in the preferred frame. The following relations, however, are left undefined:

• ${displaystyle a(v)}$ differences in time measurements,
• ${displaystyle b(v)}$ differences in measured longitudinal lengths,
• ${displaystyle d(v)}$ differences in measured transverse lengths,
• ${displaystyle varepsilon (v)}$ depends on the clock synchronization procedure in the moving frame,