Фиктивная сила - Fictitious force

Часть серии по
Классическая механика
${ displaystyle { textbf {F}} = { frac {d} {dt}} (м { textbf {v}})}$ Второй закон движения
История График Учебники
ветви Применяемый Небесный Continuum Динамика Кинематика Кинетика Статика Статистический
Основы Ускорение Угловой момент Пара Принцип Даламбера Энергия кинетический потенциал Сила Точка зрения Инерциальная система отсчета Импульс Инерция  / Момент инерции Масса Механическая мощность Механическая работа Момент Импульс Космос Скорость Время Крутящий момент Скорость Виртуальная работа
Составы Законы движения Ньютона Аналитическая механика Лагранжева механика Гамильтонова механика Рутианская механика Уравнение Гамильтона – Якоби Уравнение движения Аппеля Механика Купмана – фон Неймана
Основные темы Демпфирование  (соотношение ) Смещение Уравнения движения Законы движения Эйлера Фиктивная сила Трение Гармонический осциллятор Инерционный  / Неинерциальная система отсчета Механика движения плоских частиц Движение  (линейный ) Закон всемирного тяготения Ньютона Законы движения Ньютона Относительная скорость Жесткое тело динамика Уравнения Эйлера Простые гармонические колебания Вибрация
Вращение Круговое движение Вращающаяся опорная рамка Центростремительная сила Центробежная сила реактивный Сила Кориолиса Маятник Тангенциальная скорость Скорость вращения Угловое ускорение  / смещение  / частота  / скорость
Ученые Кеплер Галилео Гюйгенс Ньютон Хоррокс Галлей Даниэль Бернулли Иоганн Бернулли Эйлер д'Аламбер Clairaut Лагранж Лаплас Гамильтон Пуассон Коши Раут Liouville Appell Гиббс Купман фон Нейман
Категории ► Классическая механика

А фиктивная сила (также называемый псевдосила,^[1] сила Даламбера,^[2][3] или же инерционная сила^[4][5]) это сила который, кажется, действует на массу, движение которой описывается с помощью неинерциальная система отсчета, например, ускоряющий или вращающаяся система отсчета. Пример можно увидеть в пассажирском транспортном средстве, которое ускоряется в прямом направлении - пассажиры ощущают, что на них действует сила в обратном направлении, толкая их обратно на свои сиденья. Примером вращающейся системы отсчета является сила, которая, кажется, толкает объекты наружу к ободу центрифуги. Эти кажущиеся силы являются примерами фиктивных сил.

Вымышленная сила F возникает из-за инерции объекта, когда система отсчета не движется по инерции и, таким образом, начинает ускоряться относительно свободного объекта. Таким образом, фиктивная сила не возникает ни из каких физическое взаимодействие между двумя объектами, такими как электромагнетизм или же контактные силы, а скорее от разгона а из неинерциальная система отсчета сам, который с точки зрения кадра теперь кажется ускорением объекта, требующим «силы», чтобы это произошло. Как заявил Иро:^[6][7]

Такая дополнительная сила из-за неоднородного относительного движения двух систем отсчета называется псевдосила.

— Х. Иро в Современный подход к классической механике п. 180

Предполагая Второй закон Ньютона в виде F = ма, фиктивные силы всегда пропорциональны массе м.

Фиктивная сила, действующая на объект, возникает как воображаемое влияние, когда система отсчета, используемая для описания движения объекта, ускоряется по сравнению с неускоряющейся рамкой. Фиктивная сила «объясняет» с помощью механики Ньютона, почему объект не подчиняется законам Ньютона и «плавает свободно», как будто он невесомый. Как рама может ускоряться произвольно, так и фиктивные силы могут быть произвольными (но только в прямом ответе на ускорение рамы). Тем не менее, четыре фиктивных силы определены для кадров, ускоряемых обычным образом: одна вызвана любым относительным ускорением исходной точки по прямой (прямолинейная ускорение );^[8] два с вращением: центробежная сила и Сила Кориолиса; и четвертый, названный Сила Эйлера, вызванного переменной скоростью вращения, если это произойдет.

Сила гравитации также будет фиктивной силой, основанной на модели поля, в которой частицы искажают пространство-время из-за их массы, например общая теория относительности.

В инерциальной системе отсчета (верхняя часть рисунка) черный шар движется по прямой. Однако наблюдатель (коричневая точка), который находится во вращающейся / неинерциальной системе отсчета (нижняя часть изображения), видит, что объект движется по кривой траектории из-за кориолисовых и центробежных сил, присутствующих в этом кадре.

Фон

Роль фиктивных сил в механике Ньютона описывается Тоннелат:^[9]

Для Ньютона появление ускорения всегда указывает на существование абсолютного движения - абсолютного движения материи, где настоящий силы обеспокоены; абсолютное движение системы отсчета, где так называемые фиктивный силы, такие как силы инерции или силы Кориолиса.

— Мария-Антуанетта Тоннелат в Принципы электромагнитной теории и теории относительности, п. 113

Фиктивные силы возникают в классическая механика и специальная теория относительности во всех неинерциальных системах отсчета.^[10]:10 Инерциальные системы отсчета привилегированный над неинерциальными системами отсчета, потому что они не имеют физики, причины которой находятся вне системы, в то время как неинерциальные системы отсчета имеют.^[10]:209 Вымышленные силы или физика, причина которых находится вне системы, больше не нужны в общая теория относительности,^{[10]:215—223} поскольку эта физика объясняется геодезические из пространство-время.^[11]

На земле

Поверхность Земли - это вращающаяся система отсчета. Решать классическая механика задачи точно в привязанной к Земле системе отсчета, должны быть введены три фиктивные силы: Сила Кориолиса, то центробежная сила (описано ниже) и Сила Эйлера. Сила Эйлера обычно игнорируется, поскольку изменения угловой скорости вращающейся поверхности Земли обычно незначительны. Обе другие фиктивные силы слабы по сравнению с наиболее типичными силами повседневной жизни, но их можно обнаружить при тщательных условиях. Например, Леон Фуко использовал его Маятник Фуко чтобы показать, что Сила Кориолиса результат вращения Земли. Если бы Земля вращалась в двадцать раз быстрее (то есть каждый день длился бы всего ~ 72 минуты), у людей могло бы легко сложиться впечатление, что на них действуют такие фиктивные силы, как на вращающуюся карусель; людям в умеренных и тропических широтах, по сути, нужно было бы держаться, чтобы не попасть на орбиту центробежной силой.

Обнаружение неинерциальной системы отсчета

Наблюдатели внутри закрытого ящика, движущегося с постоянной скорость не может обнаружить собственное движение; однако наблюдатели в ускоряющейся системе отсчета могут обнаружить, что они находятся в неинерциальной системе отсчета, благодаря возникающим фиктивным силам. Например, для ускорения по прямой Владимир Арнольд представляет следующую теорему:^[12]

В системе координат K который движется поступательно относительно инерциальной системы k, движение механической системы происходит так, как если бы система координат была инерционной, но в каждой точке массы м действовала дополнительная «сила инерции»: F = −ма, куда а это ускорение системы K.

Другие ускорения также вызывают фиктивные силы, как описано математически. ниже. Физическое объяснение движений в инерциальной системе отсчета является наиболее простым и не требует фиктивных сил: фиктивные силы равны нулю, что позволяет отличать инерциальные системы отсчета от других.^[13]

Примером обнаружения неинерциальной вращающейся системы отсчета является прецессия Маятник Фуко. В неинерциальной системе отсчета Земли фиктивный Сила Кориолиса необходимо пояснить наблюдения. В инерциальной системе отсчета за пределами Земли такая фиктивная сила не нужна.

Примеры

Разгон по прямой

Рисунок 1: Верхняя панель: разгоняющий автомобиль массы M с массовым пассажиром м. Сила от оси равна (м + M)а. В инерциальной системе отсчета это единственная сила, действующая на автомобиль и пассажира.
Центральная панель: покомпонентное изображение в инерциальной системе отсчета. На пассажира действует ускоряющая сила ма. Сиденье (предполагаемое незначительной массой) сжимается между силой реакции -ма и приложенная сила от автомобиля ма. На автомобиль действует чистая сила ускорения. Mа то есть разница между приложенной силой (м + M)а от оси и реакция от сиденья -ма.
Нижняя панель: покомпонентное изображение в неинерциальной системе отсчета. В неинерциальной системе отсчета, где автомобиль не ускоряется, сила от оси уравновешивается фиктивной обратной силой - (м + M)а, порция -Mа применяется к автомобилю, и -ма пассажиру. Автомобиль подвержен фиктивной силе -Mа и сила (м + M)а от оси. Сумма этих сил ма прикладывается к сиденью, которое вызывает реакцию -ма на автомобиль, поэтому к автомобилю прилагается нулевая чистая сила. Сиденье (предположительно безмассовое) передает силу ма пассажиру, в отношении которого также действует фиктивная сила, -ма, в результате чего нагрузка на пассажира равна нулю. Пассажир проявляет силу реакции -ма на сиденье, которое поэтому сжимается. Во всех рамах сжатие сиденья одинаково, и сила, передаваемая осью, одинакова.

На рисунке 1 (вверху) показан разгоняющийся автомобиль. Когда машина ускоряет, пассажир чувствует, как будто его толкают обратно на сиденье. В инерциальной системе отсчета, привязанной к дороге, нет физической силы, перемещающей водителя назад. Однако в неинерциальной системе отсчета гонщика, прикрепленной к ускоряющемуся автомобилю, является обратная фиктивная сила. Мы упоминаем две возможные причины силы, чтобы прояснить ее (существование) существования:^[14]

• Рисунок 1 (центральная панель). Наблюдателю, покоящемуся на инерциальная система отсчета (как земля), машина будет ускоряться. Для того, чтобы пассажир оставался в машине, к пассажиру необходимо приложить силу. Эта сила создается сиденьем, которое начало двигаться вперед вместе с автомобилем, и прижимается к пассажиру до тех пор, пока оно не передаст полную силу, чтобы пассажир двигался вместе с автомобилем. Таким образом, силы, действующие на сиденье, неуравновешены, поэтому пассажир ускоряется в этой раме.
• Рисунок 1 (нижняя панель). С точки зрения внутренней части автомобиля, ускоряющей системы отсчета, существует фиктивная сила, толкающая пассажира назад, с величиной, равной масса пассажира умножает на ускорение автомобиля. Эта сила толкает пассажира обратно в сиденье до тех пор, пока сиденье не сжимается и не создает равную и противоположную силу. После этого пассажир неподвижен в этой рамке, потому что фиктивная сила и реальная сила сиденья уравновешены.

Обнаружено, что ускоряющая рамка не инерционна, потому что в ускоряющейся системе все кажется подверженным нулевой чистой силе и ничего не движется. Тем не менее, сжатие сиденья наблюдается и объясняется в ускоряющей системе координат (и в инерциальной системе координат) силой ускорения сиденья от автомобиля с одной стороны и противоположной силой реакции на ускорение со стороны пассажира на Другой. Идентификация ускоряющей рамы как неинерциальной не может быть основана просто на сжатии сиденья, которое могут объяснить все наблюдатели; скорее он основан на простота физического объяснения этого сжатия.

Для объяснения сжатия сиденья в ускоряющей раме требуется не только тяга от оси автомобиля, но и дополнительные (фиктивные) силы. В инерционной раме необходима только тяга от оси. Следовательно, инерциальная система отсчета имеет проще физическое объяснение (не обязательно более простая математическая формулировка), указывающее, что ускоряющаяся система координат является неинерциальной системой отсчета. Другими словами, в инерциальной системе отсчета фиктивные силы равны нулю. Видеть инерциальная система отсчета.

Этот пример показывает, как фиктивные силы возникают при переключении с инерциальной системы отсчета на неинерциальную. Расчеты физических величин (сжатие сиденья, требуемое усилие от оси), выполненные в любой системе отсчета, дают одинаковые ответы, но в некоторых случаях вычисления легче производить в неинерциальной системе отсчета. (В этом простом примере вычисления одинаково сложны для двух описанных кадров.)

Анимация: вождение от квартала к кварталу
Карта и рама автомобиля. Перспективы физических (красный) и фиктивных (синий) сил для автомобиля, движущегося от одного знака остановки к другому На этой иллюстрации автомобиль разгоняется после знака «Стоп» до середины квартала, после чего водитель немедленно выключает педаль газа и тормозит, чтобы сделать следующую остановку.

Круговое движение

Аналогичный эффект наблюдается в круговое движение, круговой с точки зрения инерциальной системы отсчета, прикрепленной к дороге. Если смотреть из неинерциальной системы отсчета, прикрепленной к автомобилю, вымышленная сила называется центробежная сила появляется. Если автомобиль движется с постоянной скоростью по круговому участку дороги, пассажиры будут чувствовать, что центробежная сила выталкивает их наружу, от центра поворота. Снова ситуацию можно рассматривать с инерциальной или неинерциальной системы отсчета:

• С точки зрения инерциальной системы отсчета, неподвижной относительно дороги, автомобиль ускоряется к центру круга. Это ускорение необходимо, потому что направление скорости меняется, несмотря на постоянную скорость. Это внутреннее ускорение называется центростремительное ускорение и требует центростремительная сила для поддержания кругового движения. Эта сила действует на колеса со стороны земли, в данном случае со стороны трение между колесами и дорогой.^[15] Автомобиль ускоряется из-за неуравновешенной силы, которая заставляет его двигаться по кругу. (Смотрите также наклонный поворот.)
• С точки зрения вращающейся рамы, движущейся вместе с автомобилем, существует фиктивная центробежная сила, которая имеет тенденцию толкать машину к внешней стороне дороги (и толкать пассажиров к внешней стороне автомобиля). Центробежная сила уравновешивает трение между колесами и дорогой, делая автомобиль неподвижным в этой неинерциальной раме.

Классическим примером фиктивной силы в круговом движении является эксперимент вращающиеся сферы связаны веревкой и вращаются вокруг своего центра масс. В этом случае, как и в примере с линейно ускоряющимся автомобилем, идентификация вращающейся неинерциальной системы отсчета может быть основана на исчезновении фиктивных сил. В инерциальной системе отсчета фиктивные силы не нужны для объяснения натяжения струны, соединяющей сферы. Во вращающейся раме должны быть введены силы Кориолиса и центробежные силы для прогнозирования наблюдаемого напряжения.

Во вращающейся системе отсчета, воспринимаемой на поверхности Земли, центробежная сила уменьшает кажущуюся силу тяжести примерно на одну тысячную, в зависимости от широты. Это уменьшение равно нулю на полюсах, максимуму на полюсах. экватор.

Анимация: объект выпущен из карусели

Отображение и вращение кадров перспективы физических (красный) и фиктивных (синий) сил для объекта, выпущенного из карусели С точки зрения фрейма карты при потере центростремительного ускорения может быть опасна скорость. С точки зрения системы вращения, опасность может заключаться в геометрическом ускорении, которое порождает эту фиктивную силу.Примечание: В некоторых браузерах нажатие [Esc] останавливает движение для более подробного анализа. Однако для перезапуска страницу, возможно, придется перезагрузить.

Фиктивный Сила Кориолиса, которое наблюдается во вращающихся системах отсчета, обычно видно только в очень крупномасштабных движениях, таких как движение снарядов дальнобойных орудий или циркуляция атмосферы Земли (см. Число Россби ). Пренебрегая сопротивлением воздуха, объект, сброшенный с башни высотой 50 метров на экваторе, упадет на 7,7 миллиметра к востоку от места ниже, где он был сброшен из-за силы Кориолиса.^[16]

В случае удаленных объектов и вращающейся системы отсчета необходимо учитывать результирующую силу центробежных сил и сил Кориолиса. Рассмотрим далекую звезду, наблюдаемую с вращающегося космического корабля. В системе отсчета, вращающейся вместе с космическим кораблем, далекая звезда движется по круговой траектории вокруг космического корабля. Кажущееся движение звезды - это кажущееся центростремительное ускорение. Как и в приведенном выше примере автомобиля, движущегося по кругу, центробежная сила имеет ту же величину, что и фиктивная центростремительная сила, но направлена ​​в противоположном, центробежном направлении. В этом случае сила Кориолиса в два раза превышает центробежную силу и указывает в центростремительном направлении. Векторная сумма центробежной силы и силы Кориолиса представляет собой полную фиктивную силу, которая в данном случае указывает в центростремительном направлении.

Фиктивные силы и работа

Можно считать, что фиктивные силы делают работай, при условии, что они перемещают объект на траектория это меняет его энергия из потенциал к кинетический. Например, представьте себе человека, сидящего на вращающемся стуле и держащего в вытянутой руке гирю. Если они тянут руку внутрь, к своему телу, с точки зрения вращающейся системы отсчета, они совершают работу против центробежной силы. Когда груз отпускается, он самопроизвольно летит наружу относительно вращающейся системы отсчета, потому что центробежная сила действует на объект, преобразовывая его потенциальную энергию в кинетическую. С инерционной точки зрения, конечно, объект улетает от них, потому что ему внезапно позволяют двигаться по прямой. Это показывает, что проделанная работа, такая как полная потенциальная и кинетическая энергия объекта, может отличаться в неинерциальной системе отсчета от инерциальной.

Гравитация как фиктивная сила

Понятие «фиктивной силы» возникло в общей теории относительности Эйнштейна.^[17][18] Все фиктивные силы пропорциональны массе объекта, на который они действуют, что также верно для сила тяжести.^[19] Это привело Альберт Эйнштейн чтобы задаться вопросом, была ли гравитация также фиктивной силой. Он отметил, что свободное падение наблюдатель в закрытом ящике не сможет обнаружить силу тяжести; следовательно, свободно падающие системы отсчета эквивалентны инерциальной системе отсчета ( принцип эквивалентности ). Следуя этому открытию, Эйнштейн смог сформулировать теорию с гравитацией как фиктивной силой и приписать кажущееся ускорение силы тяжести кривизна из пространство-время. Эта идея лежит в основе теории Эйнштейна. общая теория относительности. Видеть Эксперимент Этвёша.

Анимация: мяч, который скатывается со скалы

Дождь и ракушка создают перспективы физических (красный) и вымышленных (синий) сил для объекта, скатывающегося со скалы. Примечание: Перспектива рамы дождя здесь, а не капля дождя, больше похожа на прыжок на батуте, траектория которого завершается, когда мяч достигает края обрыва. Перспектива рамы оболочки[20] может быть знаком обитателям планет, которые каждую минуту полагаются на восходящие физические силы из окружающей среды, чтобы защитить себя от геометрического ускорения из-за искривленного пространства-времени.

Математический вывод фиктивных сил

Рисунок 2: Объект, расположенный в Икс_А в инерциальной системе отсчета А находится по адресу Икс_B в ускоряющемся кадре B. Происхождение кадра B находится в Икс_AB в кадре А. Ориентация кадра B определяется единичными векторами вдоль своих координатных направлений, ты_j с j = 1, 2, 3. Используя эти оси, координаты объекта в соответствии с кадром B находятся Икс_B = ( Икс₁, Икс₂, Икс₃ ).

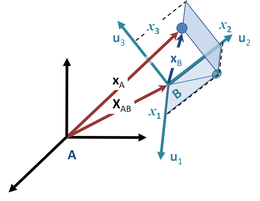
Общее происхождение

Многие задачи требуют использования неинерциальных систем отсчета, например, спутниковые.^[21][22] и ускорители частиц.^[23] На рис.2 изображена частица с масса м и позиция вектор Икс_А(т) в частности инерциальная система отсчета A. Рассмотрим неинерциальную систему отсчета B, начало которой относительно инерциальной системы определяется выражением Икс_AB(т). Пусть положение частицы в кадре B будет Икс_B(т). Какая сила действует на частицу в системе координат системы B? ^[24][25]

Чтобы ответить на этот вопрос, пусть ось координат в B представлена ​​единичными векторами ты_j с j любой из {1, 2, 3} для трех осей координат. потом

${ displaystyle mathbf {x} _ { mathrm {B}} = sum _ {j = 1} ^ {3} x_ {j} mathbf {u} _ {j} .}$

Интерпретация этого уравнения такова: Икс_B - векторное смещение частицы, выраженное через координаты в системе B в момент времени т. Из кадра А частица находится по адресу:

${ displaystyle mathbf {x} _ { mathrm {A}} = mathbf {X} _ { mathrm {AB}} + sum _ {j = 1} ^ {3} x_ {j} mathbf { u} _ {j} .}$

Кроме того, единичные векторы {ты_j } не может изменять величину, поэтому производные этих векторов выражают только поворот системы координат B. С другой стороны, вектор Икс_AB просто определяет начало координат кадра B относительно кадра A и поэтому не может включать поворот кадра B.

Взяв производную по времени, скорость частицы равна:

${ displaystyle { frac {d mathbf {x} _ { mathrm {A}}} {dt}} = { frac {d mathbf {X} _ { mathrm {AB}}} {dt}} + sum _ {j = 1} ^ {3} { frac {dx_ {j}} {dt}} mathbf {u} _ {j} + sum _ {j = 1} ^ {3} x_ { j} { frac {d mathbf {u} _ {j}} {dt}} .}$

Второй член суммирования - это скорость частицы, скажем v_B как измерено в кадре B. То есть:

${ displaystyle { frac {d mathbf {x} _ { mathrm {A}}} {dt}} = mathbf {v} _ { mathrm {AB}} + mathbf {v} _ { mathrm {B}} + sum _ {j = 1} ^ {3} x_ {j} { frac {d mathbf {u} _ {j}} {dt}}.}$

Интерпретация этого уравнения состоит в том, что скорость частицы, видимой наблюдателями в системе A, состоит из того, что наблюдатели в системе B называют скоростью, а именно v_B, плюс два дополнительных члена, связанных со скоростью изменения осей координат кадра B. Один из них - просто скорость движущегося источника. v_AB. Другой - вклад в скорость из-за того, что разные точки в неинерциальной системе отсчета имеют разные кажущиеся скорости из-за вращения системы координат; точка, видимая из вращающейся рамки, имеет вращательную составляющую скорости, которая тем больше, чем дальше точка от начала координат.

Чтобы найти ускорение, другое временное дифференцирование предусматривает:

${ displaystyle { frac {d ^ {2} mathbf {x} _ { mathrm {A}}} {dt ^ {2}}} = mathbf {a} _ { mathrm {AB}} + { frac {d mathbf {v} _ { mathrm {B}}} {dt}} + sum _ {j = 1} ^ {3} { frac {dx_ {j}} {dt}} { гидроразрыв {d mathbf {u} _ {j}} {dt}} + sum _ {j = 1} ^ {3} x_ {j} { frac {d ^ {2} mathbf {u} _ { j}} {dt ^ {2}}}.}$

Используя ту же формулу, которая уже использовалась для производной по времени от Икс_B, производная скорости справа равна:

${ displaystyle { frac {d mathbf {v} _ { mathrm {B}}} {dt}} = sum _ {j = 1} ^ {3} { frac {dv_ {j}} {dt }} mathbf {u} _ {j} + sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}} = mathbf {a} _ { mathrm {B}} + sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}}.}$

Как следствие,

${ displaystyle { frac {d ^ {2} mathbf {x} _ { mathrm {A}}} {dt ^ {2}}} = mathbf {a} _ { mathrm {AB}} + mathbf {a} _ { mathrm {B}} +2 sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}} + sum _ {j = 1} ^ {3} x_ {j} { frac {d ^ {2} mathbf {u} _ {j}} {dt ^ {2}}}.}$

(1)

Интерпретация этого уравнения следующая: ускорение частицы в системе A состоит из того, что наблюдатели в системе B называют ускорением частицы. а_B, но, кроме того, есть три члена ускорения, связанные с движением осей координат кадра B: один член, связанный с ускорением начала координат кадра B, а именно а_AB, и два члена, относящиеся к повороту рамки B.Следовательно, наблюдатели в B будут видеть движение частицы как обладающее «дополнительным» ускорением, которое они будут приписывать «силам», действующим на частицу, но которые наблюдатели в A говорят, являются «фиктивными» силами, возникающими просто потому, что наблюдатели в B не распознают неинерционный характер рамы B.

Коэффициент два в силе Кориолиса возникает из двух равных вкладов: (i) кажущееся изменение инерционно постоянной скорости со временем, потому что вращение заставляет направление скорости, как кажется, меняется (a dv_B/ дт член) и (ii) очевидное изменение скорости объекта при изменении его положения, когда он приближается к оси вращения или дальше от нее (изменение ${ displaystyle sum x_ {j} , d mathbf {u} _ {j} / dt}$ из-за изменения в Икс _j ).

Чтобы выразить суть дела в силах, ускорение умножается на массу частицы:

${ displaystyle mathbf {F} _ { mathrm {A}} = mathbf {F} _ { mathrm {B}} + m mathbf {a} _ { mathrm {AB}} + 2m sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}} + m sum _ {j = 1} ^ {3} x_ {j} { frac {d ^ {2} mathbf {u} _ {j}} {dt ^ {2}}} .}$

Сила, наблюдаемая в кадре B, F_B = ма_B связана с действительной силой, действующей на частицу, F_А, к

${ displaystyle mathbf {F} _ { mathrm {B}} = mathbf {F} _ { mathrm {A}} + mathbf {F} _ { mathrm {fictitious}},}$

куда:

${ displaystyle mathbf {F} _ { mathrm {fictitious}} = - m mathbf {a} _ { mathrm {AB}} -2m sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}} - m sum _ {j = 1} ^ {3} x_ {j} { frac {d ^ {2} mathbf {u } _ {j}} {dt ^ {2}}} .}$

Таким образом, мы можем решить проблемы в системе отсчета B, предполагая, что выполняется второй закон Ньютона (относительно величин в этой системе отсчета), и рассматривая F_{фиктивный} как дополнительная сила.^[12][26][27]

Ниже приводится ряд примеров применения этого результата для фиктивных сил. Больше примеров можно найти в статье о центробежная сила.

Вращающиеся системы координат

Обычная ситуация, в которой полезны неинерциальные системы отсчета, - это когда система отсчета вращается. Поскольку такое вращательное движение не является инерционным, из-за ускорения, присутствующего в любом вращательном движении, фиктивная сила всегда может быть вызвана с использованием вращательной системы отсчета. Несмотря на эту сложность, использование фиктивных сил часто упрощает необходимые вычисления.

Чтобы получить выражения для фиктивных сил, необходимы производные для кажущейся скорости изменения векторов во времени, которые учитывают изменение во времени осей координат. Если вращение кадра 'B' представлено вектором Ω направлен вдоль оси вращения с ориентацией, заданной правило правой руки, а величина определяется как

${ displaystyle | { boldsymbol { Omega}} | = { frac {d theta} {dt}} = omega (t),}$

тогда производная по времени любого из трех единичных векторов, описывающих кадр B, равна^[26][28]

${ displaystyle { frac {d mathbf {u} _ {j} (t)} {dt}} = { boldsymbol { Omega}} times mathbf {u} _ {j} (t),}$

и

${ displaystyle { frac {d ^ {2} mathbf {u} _ {j} (t)} {dt ^ {2}}} = { frac {d { boldsymbol { Omega}}} {dt }} times mathbf {u} _ {j} + { boldsymbol { Omega}} times { frac {d mathbf {u} _ {j} (t)} {dt}} = { frac {d { boldsymbol { Omega}}} {dt}} times mathbf {u} _ {j} + { boldsymbol { Omega}} times left [{ boldsymbol { Omega}} times mathbf {u} _ {j} (t) right],}$

как проверено с использованием свойств векторное произведение. Эти производные формулы теперь применяются к соотношению между ускорением в инерциальной системе координат и ускорением в системе координат, вращающейся с изменяющейся во времени угловой скоростью ω (т). Из предыдущего раздела, где индекс A относится к инерциальной системе координат, а B - к вращающейся системе координат, установка а_AB = 0, чтобы удалить любое поступательное ускорение и сосредоточиться только на вращательных свойствах (см. Уравнение 1 ):

${ displaystyle { frac {d ^ {2} mathbf {x} _ { mathrm {A}}} {dt ^ {2}}} = mathbf {a} _ { mathrm {B}} +2 sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}} + sum _ {j = 1} ^ {3} x_ {j} { frac {d ^ {2} mathbf {u} _ {j}} {dt ^ {2}}},}$

${ displaystyle mathbf {a} _ { mathrm {A}} = mathbf {a} _ { mathrm {B}} + 2 sum _ {j = 1} ^ {3} v_ {j} { boldsymbol { Omega}} times mathbf {u} _ {j} (t) + sum _ {j = 1} ^ {3} x_ {j} { frac {d { boldsymbol { Omega} }} {dt}} times mathbf {u} _ {j} + sum _ {j = 1} ^ {3} x_ {j} { boldsymbol { Omega}} times left [{ полужирный символ { Omega}} times mathbf {u} _ {j} (t) right]}$

${ displaystyle = mathbf {a} _ { mathrm {B}} +2 { boldsymbol { Omega}} times sum _ {j = 1} ^ {3} v_ {j} mathbf {u} _ {j} (t) + { frac {d { boldsymbol { Omega}}} {dt}} times sum _ {j = 1} ^ {3} x_ {j} mathbf {u} _ {j} + { boldsymbol { Omega}} times left [{ boldsymbol { Omega}} times sum _ {j = 1} ^ {3} x_ {j} mathbf {u} _ { j} (t) right].}$

Собирая термины, получается так называемый формула преобразования ускорения:^[29]

${ displaystyle mathbf {a} _ { mathrm {A}} = mathbf {a} _ { mathrm {B}} +2 { boldsymbol { Omega}} times mathbf {v} _ { mathrm {B}} + { frac {d { boldsymbol { Omega}}} {dt}} times mathbf {x} _ { mathrm {B}} + { boldsymbol { Omega}} times left ({ boldsymbol { Omega}} times mathbf {x} _ { mathrm {B}} right) .}$

В физическое ускорение а_А из-за чего наблюдатели в инерциальной системе отсчета A звонят реальные внешние силы на объекте, следовательно, не просто ускорение а_B видимые наблюдателями в системе вращения B, но имеет несколько дополнительных геометрических элементов ускорения, связанных с вращением B. Как видно в системе координат вращения, ускорение а_B частицы задается перестановкой приведенного выше уравнения как:

${ displaystyle mathbf {a} _ { mathrm {B}} = mathbf {a} _ { mathrm {A}} -2 { boldsymbol { Omega}} times mathbf {v} _ { mathrm {B}} - { boldsymbol { Omega}} times ({ boldsymbol { Omega}} times mathbf {x} _ { mathrm {B}}) - { frac {d { boldsymbol { Omega}}} {dt}} times mathbf {x} _ { mathrm {B}}.}$

Чистая сила, действующая на объект, по мнению наблюдателей во вращающейся рамке, равна F_B = ма_B. Если их наблюдения должны привести к правильной силе, действующей на объект при использовании законов Ньютона, они должны учитывать, что дополнительная сила F_фикция присутствует, поэтому конечный результат F_B = F_А + F_фикция. Таким образом, фиктивная сила, используемая наблюдателями в B, чтобы получить правильное поведение объекта из законов Ньютона, равна:

${ displaystyle mathbf {F} _ { mathrm {fict}} = - 2m { boldsymbol { Omega}} times mathbf {v} _ { mathrm {B}} -m { boldsymbol { Omega }} times ({ boldsymbol { Omega}} times mathbf {x} _ { mathrm {B}}) - m { frac {d { boldsymbol { Omega}}} {dt}} раз mathbf {x} _ { mathrm {B}}.}$

Здесь первый член - это Сила Кориолиса,^[30] второй член - это центробежная сила,^[31] а третий член - это Сила Эйлера.^[32][33]

Орбитальные системы координат

Рисунок 3: Орбитальная, но фиксированная система координат ориентации B, показанный в три разных раза. Единичные векторы ты_j, j = 1, 2, 3 сделать нет повернуть, но сохранить фиксированную ориентацию, в то время как начало системы координат B движется с постоянной угловой скоростью ω вокруг неподвижной оси Ω. Ось Ω проходит через начало инерциальной системы отсчета А, поэтому происхождение кадра B фиксированное расстояние р от начала инерциальной системы отсчета А.

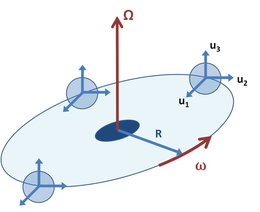
В качестве связанного примера предположим, что движущаяся система координат B вращается с постоянной угловой скоростью ω по окружности радиуса р о фиксированном начале инерциальной системы отсчета А, но сохраняет его оси координат фиксированной ориентацией, как на рисунке 3. Ускорение наблюдаемого тела теперь равно (см. Уравнение 1 ):

${ displaystyle { frac {d ^ {2} mathbf {x} _ {A}} {dt ^ {2}}} = mathbf {a} _ {AB} + mathbf {a} _ {B} +2 sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}}}$ ${ displaystyle + sum _ {j = 1} ^ {3} x_ {j} { frac {d ^ {2} mathbf {u} _ {j}} {dt ^ {2}}} . }$

${ displaystyle = mathbf {a} _ {AB} + mathbf {a} _ {B} ,}$

где суммы равны нулю, поскольку единичные векторы не зависят от времени. Происхождение системы B расположен согласно раме А в:

${ Displaystyle mathbf {X} _ {AB} = R left ( cos ( omega t), sin ( omega t) right) ,}$

приводящая к скорости начала координат кадра B в качестве:

${ displaystyle mathbf {v} _ {AB} = { frac {d} {dt}} mathbf {X} _ {AB} = mathbf { Omega times X} _ {AB} ,}$

приводящий к ускорению происхождения B предоставлено:

${ displaystyle mathbf {a} _ {AB} = { frac {d ^ {2}} {dt ^ {2}}} mathbf {X} _ {AB}}$ ${ displaystyle = mathbf { Omega times} left ( mathbf { Omega times X} _ {AB} right)}$ ${ displaystyle = - omega ^ {2} mathbf {X} _ {AB} .}$

Потому что первый член, который

${ Displaystyle mathbf { Omega times} left ( mathbf { Omega times X} _ {AB} right) ,}$

имеет ту же форму, что и выражение нормальной центробежной силы:

${ displaystyle { boldsymbol { Omega}} times left ({ boldsymbol { Omega}} times mathbf {x} _ {B} right) ,}$

термин «центробежная сила» является естественным расширением стандартной терминологии (хотя стандартной терминологии для этого случая нет). Какая бы терминология ни использовалась, наблюдатели в кадре B должны ввести фиктивную силу, на этот раз из-за ускорения от орбитального движения всей их системы координат, то есть радиально наружу от центра вращения начала их системы координат:

${ Displaystyle mathbf {F} _ { mathrm {fict}} = м omega ^ {2} mathbf {X} _ {AB} ,}$

и по величине:

${ displaystyle | mathbf {F} _ { mathrm {fict}} | = m omega ^ {2} R .}$

Обратите внимание, что эта «центробежная сила» отличается от случая вращающейся рамы. Во вращающейся раме центробежная сила связана с расстоянием от объекта до начала рамы. B, тогда как в случае орбитального кадра центробежная сила не зависит от расстояния объекта от начала кадра B, но вместо этого зависит от расстояния до начала кадра B из это центр вращения, в результате чего одно и тоже центробежная фиктивная сила для все объекты наблюдаемые в кадре B.

Орбита и вращение

Рисунок 4: Орбитальная система координат B аналогично рисунку 3, но в котором единичные векторы ты_j, j = 1, 2, 3 повернутся к оси вращения, а начало системы координат B движется с постоянной угловой скоростью ω вокруг неподвижной оси Ω.

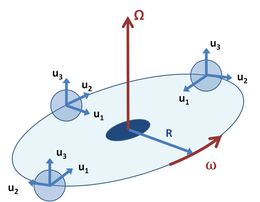
В качестве примера комбинации на рисунке 4 показана система координат B который вращается вокруг инерциальной системы отсчета А как на рисунке 3, но оси координат в кадре B повернуть так единичный вектор ты₁ всегда указывает в сторону центра вращения. Этот пример может применяться к пробирке в центрифуге, где вектор ты₁ указывает вдоль оси трубки в сторону ее отверстия наверху. Он также напоминает систему Земля-Луна, где Луна всегда обращена к Земле одним лицом.^[34] В этом примере единичный вектор ты₃ сохраняет фиксированную ориентацию, а векторы ты₁, ты₂ вращаются с той же скоростью, что и начало координат. Это,

${ Displaystyle mathbf {и} _ {1} = (- соз омега т, - грех омега т) ; }$ ${ displaystyle mathbf {u} _ {2} = ( sin omega t, - cos omega t) .}$

${ displaystyle { frac {d} {dt}} mathbf {u} _ {1} = mathbf { Omega times u_ {1}} = omega mathbf {u} _ {2} ;}$ ${ displaystyle { frac {d} {dt}} mathbf {u} _ {2} = mathbf { Omega times u_ {2}} = - omega mathbf {u} _ {1} .}$

Следовательно, ускорение движущегося объекта выражается как (см. Уравнение 1 ):

${ displaystyle { frac {d ^ {2} mathbf {x} _ {A}} {dt ^ {2}}} = mathbf {a} _ {AB} + mathbf {a} _ {B} +2 sum _ {j = 1} ^ {3} v_ {j} { frac {d mathbf {u} _ {j}} {dt}}}$ ${ displaystyle + sum _ {j = 1} ^ {3} x_ {j} { frac {d ^ {2} mathbf {u} _ {j}} {dt ^ {2}}} }$

${ displaystyle = mathbf { Omega times} left ( mathbf { Omega times X} _ {AB} right) + mathbf {a} _ {B} +2 sum _ {j = 1} ^ {3} v_ {j} mathbf { Omega times u_ {j}}}$ ${ displaystyle + sum _ {j = 1} ^ {3} x_ {j} { boldsymbol { Omega}} times left ({ boldsymbol { Omega}} times mathbf {u } _ {j} right) }$

${ displaystyle = mathbf { Omega times} left ( mathbf { Omega times X} _ {AB} right) + mathbf {a} _ {B} +2 { boldsymbol { Омега}} times mathbf {v} _ {B} }$ ${ displaystyle + { boldsymbol { Omega}} times left ({ boldsymbol { Omega}} times mathbf {x} _ {B} right) }$

${ displaystyle = mathbf { Omega times} left ( mathbf { Omega times} ( mathbf {X} _ {AB} + mathbf {x} _ {B}) right) + mathbf {a} _ {B} +2 { boldsymbol { Omega}} times mathbf {v} _ {B} ,}$

где член углового ускорения равен нулю для постоянной скорости вращения, потому что первый член, который

${ displaystyle mathbf { Omega times} left ( mathbf { Omega times} ( mathbf {X} _ {AB} + mathbf {x} _ {B}) right) ,}$

имеет ту же форму, что и выражение нормальной центробежной силы:

${ displaystyle { boldsymbol { Omega}} times left ({ boldsymbol { Omega}} times mathbf {x} _ {B} right) ,}$

это естественное расширение стандартной терминологии (хотя стандартной терминологии для этого случая нет) называть этот термин «центробежная сила». Применяя эту терминологию к примеру с пробиркой в ​​центрифуге, если пробирка находится достаточно далеко от центра вращения, |Икс_AB| = р ≫ |Икс_B|, все вещество в пробирке испытывает одинаковое ускорение (одинаковую центробежную силу). Таким образом, в этом случае фиктивная сила - это, прежде всего, равномерная центробежная сила вдоль оси трубы, вдали от центра вращения, со значением |F_Фикция| = ω² р, куда р - это расстояние вещества в пробирке от центра центрифуги. Стандартной спецификацией центрифуги является использование «эффективного» радиуса центрифуги для оценки ее способности обеспечивать центробежную силу. Таким образом, первая оценка центробежной силы в центрифуге может быть основана на расстоянии пробирок от центра вращения и внесении поправок при необходимости.^[35][36]

Кроме того, пробирка ограничивает движение в направлении вниз по длине пробирки, поэтому v_B противоположен ты₁ а сила Кориолиса противоположна ты₂, то есть к стенке трубки. Если трубку вращать достаточно долго, скорость v_B падает до нуля, когда материя приходит к равновесному распределению. Подробнее читайте в статьях на осаждение и Уравнение Ламма.

Связанная с этим проблема - это проблема центробежных сил для системы Земля-Луна-Солнце, где возникают три вращения: суточное вращение Земли вокруг своей оси, вращение системы Земля-Луна за лунный месяц вокруг своего центра масс и годовой оборот системы Земля-Луна вокруг Солнца. Эти три движения влияют на приливы.^[37]

Пересечение карусели

Рисунок 5: Пересечение вращающейся карусели, идущей с постоянной скоростью от центра карусели к ее краю, спираль очерчена в инерциальной системе отсчета, в то время как простой прямой радиальный путь виден в кадре карусели.

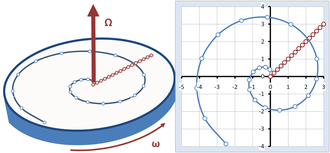
На рисунке 5 показан еще один пример сравнения наблюдений инерциального наблюдателя с наблюдениями на вращающемся карусель.^[38] Карусель вращается с постоянной угловой скоростью, представленной вектором Ω с величиной ω, направленной вверх в соответствии с правило правой руки. Наездник на карусели движется по ней в радиальном направлении с постоянной скоростью, что для пешехода выглядит как прямая линия, наклоненная под углом 45 ° на рис. 5. Однако для неподвижного наблюдателя он движется по спиральной траектории. Точки, обозначенные на обоих путях на Рисунке 5, соответствуют одинаковым временам, разнесенным через равные интервалы времени. Мы спрашиваем, как два наблюдателя, один на карусели, а другой в инерциальной системе отсчета, формулируют то, что они видят, используя законы Ньютона.

Инерционный наблюдатель

Наблюдатель в состоянии покоя описывает путь, пройденный пешеходом, как спираль. В системе координат, показанной на рисунке 5, траектория описывается следующим образом: р(т):

${ displaystyle mathbf {r} (t) = R (t) mathbf {u} _ {R} = { begin {bmatrix} x (t) y (t) end {bmatrix}} = { begin {bmatrix} R (t) cos ( omega t + pi / 4) R (t) sin ( omega t + pi / 4) end {bmatrix}},}$

где добавленное π / 4 устанавливает начальный угол траектории 45 ° (просто произвольный выбор направления), ты_р - единичный вектор в радиальном направлении, указывающий от центра карусели к шагающему в момент времени т. Радиальное расстояние р(т) неуклонно возрастает со временем в соответствии с:

${ Displaystyle R (t) = st,}$

с s скорость ходьбы. Согласно простой кинематике, тогда скорость является первой производной траектории:

${ displaystyle mathbf {v} (t) = { frac {dR} {dt}} { begin {bmatrix} cos ( omega t + pi / 4) sin ( omega t + pi / 4) end {bmatrix}} + omega R (t) { begin {bmatrix} - sin ( omega t + pi / 4) cos ( omega t + pi / 4) end {bmatrix }}}$

${ displaystyle = { frac {dR} {dt}} mathbf {u} _ {R} + omega R (t) mathbf {u} _ { theta},}$

с ты_θ единичный вектор, перпендикулярный ты_р вовремя т (в этом можно убедиться, заметив, что вектор скалярное произведение с радиальным вектором, равным нулю) и указывает направление движения. Ускорение является первой производной скорости:

${ displaystyle mathbf {a} (t) = { frac {d ^ {2} R} {dt ^ {2}}} { begin {bmatrix} cos ( omega t + pi / 4) sin ( omega t + pi / 4) end {bmatrix}} + 2 { frac {dR} {dt}} omega { begin {bmatrix} - sin ( omega t + pi / 4) cos ( omega t + pi / 4) end {bmatrix}} - omega ^ {2} R (t) { begin {bmatrix} cos ( omega t + pi / 4) sin ( omega t + pi / 4) end {bmatrix}}}$

${ displaystyle = 2s omega { begin {bmatrix} - sin ( omega t + pi / 4) cos ( omega t + pi / 4) end {bmatrix}} - omega ^ {2 } R (t) { begin {bmatrix} cos ( omega t + pi / 4) sin ( omega t + pi / 4) end {bmatrix}}}$

${ Displaystyle = 2s omega mathbf {u} _ { theta} - omega ^ {2} R (t) mathbf {u} _ {R} .}$

Последний член в ускорении направлен радиально внутрь на величину ω² р, что, следовательно, является мгновенным центростремительное ускорение из круговое движение.^[39] Первый член перпендикулярен радиальному направлению и указывает направление движения. Его величина составляет 2sω, и он представляет собой ускорение пешехода по мере приближения к краю карусели, и дуга окружности, пройденная за фиксированное время, увеличивается, как можно видеть по увеличенному интервалу между точками для равных временных шагов на спирали на рисунке 5 по мере приближения к внешнему краю карусели.

Применяя законы Ньютона, умножая ускорение на массу пешехода, инерционный наблюдатель приходит к выводу, что на пешехода действуют две силы: направленная внутрь радиально центростремительная сила и другая сила, перпендикулярная радиальному направлению, которая пропорциональна скорости движения человека. ходок.

Вращающийся наблюдатель

Вращающийся наблюдатель видит, что шагающий движется по прямой от центра карусели к периферии, как показано на рисунке 5. Более того, вращающийся наблюдатель видит, что шагающий движется с постоянной скоростью в том же направлении, поэтому применяя закон Ньютона инерция, есть нуль сила на ходока. Эти выводы не согласуются с инерционным наблюдателем. Чтобы достичь согласия, вращающийся наблюдатель должен ввести фиктивные силы, которые кажутся существующими во вращающемся мире, даже если для них нет явной причины, никакой видимой гравитационной массы, электрического заряда или чего-то еще, что могло бы объяснить эти фиктивные силы. .

Чтобы согласиться с инерциальным наблюдателем, силы, приложенные к шагающему, должны быть точно такими, как указано выше. Их можно связать с уже выведенными общими формулами, а именно:

${ displaystyle mathbf {F} _ { mathrm {fict}} = - 2m { boldsymbol { Omega}} times mathbf {v} _ { mathrm {B}} -m { boldsymbol { Omega }} times ({ boldsymbol { Omega}} times mathbf {x} _ { mathrm {B}}) - m { frac {d { boldsymbol { Omega}}} {dt}} раз mathbf {x} _ { mathrm {B}}.}$

В этом примере скорость во вращающейся рамке равна:

${ Displaystyle mathbf {v} _ { mathrm {B}} = s mathbf {u} _ {R},}$

с ты_р единичный вектор в радиальном направлении. Положение ходунка, как видно на карусели:

${ Displaystyle mathbf {x} _ { mathrm {B}} = R (t) mathbf {u} _ {R},}$

и производная по времени от Ω равен нулю для равномерного углового вращения. Заметив, что

${ displaystyle { boldsymbol { Omega}} times mathbf {u} _ {R} = omega mathbf {u} _ { theta} }$

и

${ displaystyle { boldsymbol { Omega}} times mathbf {u} _ { theta} = - omega mathbf {u} _ {R} ,}$

мы нашли:

${ displaystyle mathbf {F} _ { mathrm {fict}} = - 2m omega s mathbf {u} _ { theta} + m omega ^ {2} R (t) mathbf {u} _ {Р}.}$

Чтобы получить прямолинейное движение Во вращающемся мире сила, точно противоположная по знаку фиктивной силе, должна быть применена, чтобы уменьшить результирующую силу, действующую на пешехода, до нуля, поэтому закон инерции Ньютона будет предсказывать движение по прямой в соответствии с тем, что видит вращающийся наблюдатель. Фиктивные силы, с которыми необходимо бороться, - это Сила Кориолиса (первый срок) и центробежная сила (второй срок). (Эти сроки являются приблизительными.^[40]) Применяя силы для противодействия этим двум фиктивным силам, вращающийся наблюдатель в конечном итоге прикладывает к ходящему точно такие же силы, которые, как предсказывал инерционный наблюдатель, были необходимы.

Поскольку они отличаются только постоянной скоростью ходьбы, шагающий и наблюдатель вращения видят одинаковые ускорения. С точки зрения пешехода, фиктивная сила воспринимается как реальная, и борьба с этой силой необходима, чтобы оставаться на прямом радиальном пути с постоянной скоростью. Это похоже на борьбу с боковым ветром, когда вас отбрасывает к краю карусели.

Наблюдение

Обратите внимание, что это кинематический обсуждение не вникает в механизм, с помощью которого генерируются необходимые силы. Это предмет кинетика. В случае карусели кинетическое обсуждение могло бы включать, возможно, изучение обуви ходунка и трения, которое они должны создать о пол карусели, или, возможно, динамики скейтбординга, если ходунок переключился на передвижение на скейтборде. Какими бы ни были средства передвижения по карусели, вычисленные выше силы должны быть реализованы. Очень грубая аналогия - отопление вашего дома: у вас должна быть определенная температура, чтобы вам было комфортно, но нагреваете ли вы газом или сжиганием угля - другая проблема. Кинематика устанавливает термостат, кинетика зажигает печь.

Смотрите также

Примечания

дальнейшее чтение

• Лев Д. Ландау и Э. М. Лифшиц (1976). Механика. Курс теоретической физики. Vol. 1 (3-е изд.). Баттерворт-Хейненан. С. 128–130. ISBN  0-7506-2896-0.
• Кейт Саймон (1971). Механика (3-е изд.). Эддисон-Уэсли. ISBN  0-201-07392-7.
• Джерри Б. Марион (1970). Классическая динамика частиц и систем. Академическая пресса. ISBN  0-12-472252-0.
• Марсель Дж. Сиди (1997). Динамика и управление космическими аппаратами: практический инженерный подход. Издательство Кембриджского университета. Глава 4.8. ISBN  0-521-78780-7.

внешняя ссылка

• Вопросы и ответы от Ричарда К. Брилла, Общественный колледж Гонолулу
• Дэвид Стерн из НАСА: Планы уроков для учителей №23 Инерционные силы
• Сила Кориолиса
• Движение по плоской поверхности Ява-физлет Брайана Фидлера, иллюстрирующий фиктивные силы. Физлет показывает перспективу как с вращающейся, так и с невращающейся точки зрения.
• Движение по параболической поверхности Ява-физлет Брайана Фидлера, иллюстрирующий фиктивные силы. Физлет показывает перспективу как с вращающейся, так и с невращающейся точки зрения.