Отношение доза-реакция - Википедия - Dose–response relationship
Эта статья нужны дополнительные цитаты для проверка. (Август 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |

В зависимость доза-реакция, или же отношение "воздействие-реакция", описывает величину отклик из организм, как функция воздействия (или дозы ) к стимул или же стрессор (обычно химический ) после определенного времени выдержки.[1] Отношения "доза-реакция" можно описать следующим образом: кривые доза-реакция. Это объясняется далее в следующих разделах. А функция ответа на стимул или же кривая ответа на стимул в более широком смысле определяется как реакция на любой тип раздражителя, не ограничиваясь химическими веществами.
Мотивация к изучению зависимости "доза-реакция"
Изучение реакции на дозу и разработка моделей реакции на дозу имеет центральное значение для определения «безопасных», «опасных» и (где уместно) полезных уровней и дозировок лекарств, загрязняющих веществ, пищевых продуктов и других веществ, к которым люди или другие организмы выставлены. Эти выводы часто являются основой государственной политики. В Агентство по охране окружающей среды США разработала подробное руководство и отчеты по моделированию и оценке доза-реакция, а также программное обеспечение.[2] В Управление по санитарному надзору за качеством пищевых продуктов и медикаментов США также есть руководство по выяснению зависимости доза-реакция[3] во время разработки препарата. Отношения «доза-ответ» можно использовать для отдельных лиц или популяций. Пословица Доза делает яд отражает то, что небольшое количество токсина не оказывает значительного воздействия, в то время как большое количество может быть фатальным. Это отражает то, как отношения "доза-реакция" могут быть использованы у людей. В популяциях отношения "доза-реакция" могут описывать то, как группы людей или организмов подвергаются воздействию на разных уровнях воздействия. Зависимость доза-ответ, смоделированная кривыми доза-реакция, широко используется в фармакологии и разработке лекарственных средств. В частности, форма кривой зависимости реакции от дозы лекарственного средства (количественно определяемая параметрами EC50, nH и ymax) отражает биологическую активность и силу лекарственного средства.
Примеры стимулов и ответов
Некоторые примеры показателей зависимости доза – реакция показаны в таблицах ниже. Каждому сенсорному стимулу соответствует определенный сенсорный рецептор, например никотиновый ацетилхолиновый рецептор никотина, или механорецептор для механического давления. Однако стимулы (например, температура или излучение) могут также влиять на физиологические процессы, выходящие за рамки ощущений (и даже давать измеримую реакцию смерти). Ответы могут быть записаны как непрерывные данные (например, сила сокращения мышц) или дискретные данные (например, количество смертей).
| Пример стимула | Цель | |
|---|---|---|
| Препарат, средство, медикамент /Токсин доза | Агонист (например. никотин, изопреналин ) | Биохимические рецепторы, Ферменты, Транспортеры |
| Антагонист (например. кетамин, пропранолол ) | ||
| Аллостерический модулятор (например. Бензодиазепин ) | ||
| Температура | Рецепторы температуры | |
| Уровни звука | Клетки волос | |
| Освещение / интенсивность света | Фоторецепторы | |
| Механическое давление | Механорецепторы | |
| Доза патогена (например, LPS ) | н / д | |
| Радиация интенсивность | н / д | |
| Системный уровень | Пример ответа |
|---|---|
| численность населения (Эпидемиология ) | Смерть,[4] потеря сознания |
| Организм / Целое животное (Физиология ) | Тяжесть поражения,[4] артериальное давление,[4] частота сердечных сокращений, степень движения, внимательность, ЭЭГ данные |
| Орган /Ткань | Производство АТФ, пролиферация, сокращение мышц, производство желчи, гибель клеток |
| Клетка (Клеточная биология, Биохимия ) | Продукция АТФ, кальциевые сигналы, морфология, митоз |
Анализ и построение кривых доза-реакция
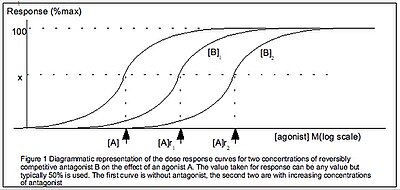
Построение кривых доза – реакция
А кривая доза-ответ это координатный график соотнося величину стимула с реакцией рецептор. Ряд эффектов (или конечные точки ) можно изучить. Измеренная доза обычно откладывается по оси X, а отклик - по оси Y. В некоторых случаях это логарифм дозы, нанесенной на ось X, и в таких случаях кривая обычно сигмовидный, с самым крутым участком посередине. Биологически обоснованные модели, использующие дозу, предпочтительнее использования логарифма (дозы), поскольку последний может визуально подразумевать пороговую дозу, когда на самом деле ее нет.[нужна цитата ]
Статистический анализ кривых доза-ответ может быть выполнен с помощью методов регрессии, таких как пробит модель или же логит модель или другие методы, такие как метод Спирмена-Карбера.[5] Эмпирические модели, основанные на нелинейной регрессии, обычно предпочтительнее использования некоторого преобразования данных, которое линеаризует зависимость доза-реакция.[6]
Типичный экспериментальный план для измерения зависимости доза-реакция: органная ванна препараты, анализы связывания лиганда, функциональные анализы, и клинические испытания лекарств.
Уравнение Хилла
Логарифмические кривые доза-реакция обычно представляют собой сигмовидный и однофазный и может быть вписан в классический Уравнение Хилла. Уравнение Хилла - это логистическая функция относительно логарифма дозы и аналогичен логит модель. Также была предложена обобщенная модель для многофазных случаев.[7]
Уравнение Хилла представляет собой следующую формулу, где величина отклика, - концентрация лекарственного средства (или, что то же самое, интенсивность стимула) и - это концентрация препарата, обеспечивающая максимальный ответ 50%, и в Коэффициент Хилла.
Параметры кривой доза-ответ отражают измерения потенция (например, EC50, IC50, ED50 и т. д.) и меры эффективности (например, тканевый, клеточный или популяционный ответ).
Обычно используемая кривая доза-ответ - это EC50 кривая, половина максимальной эффективной концентрации, где ЕС50 точка определяется как точка перегиба кривой.
Кривые доза-ответ обычно подгоняются к Уравнение Хилла.
Первая точка на графике, где достигается реакция выше нуля (или выше контрольной реакции), обычно называется пороговой дозой. Для большинства полезных или рекреационных препаратов желаемый эффект достигается при дозах, немного превышающих пороговую. При более высоких дозах нежелательные побочные эффекты появляются и становятся сильнее по мере увеличения дозы. Чем сильнее определенное вещество, тем круче будет кривая. В количественных ситуациях ось Y часто обозначается процентами, которые относятся к проценту подвергшихся воздействию людей, регистрирующих стандартный ответ (который может быть смертью, как в LD50 ). Такая кривая называется квантовой кривой доза-реакция, что отличает ее от градуированной кривой доза-реакция, где ответ является непрерывным (измеренным или оцененным).
Уравнение Хилла можно использовать для описания зависимостей "доза-реакция", например, зависимости вероятности открытия ионного канала от концентрации лиганда.[9]
Доза обычно выражается в миллиграммах. микрограммы, или граммы на килограмм веса тела при оральном воздействии, или миллиграммы на кубический метр окружающего воздуха при ингаляционном воздействии. Другие единицы дозы включают количество молей на массу тела, количество молей на животное, а для воздействия на кожу - количество молей на квадратный сантиметр.
Ограничения
Концепция линейной зависимости доза-реакция, пороговых значений и ответов типа «все или ничего» может не применяться к нелинейным ситуациям. А пороговая модель или же линейная беспороговая модель может быть более подходящим, в зависимости от обстоятельств. Недавняя критика этих моделей применительно к эндокринным разрушителям приводит к существенному пересмотру тестовых и токсикологических моделей при низких дозах из-за наблюдаемых ненормальныхмонотонность, т.е. U-образные кривые доза / ответ.[10]
Зависимость доза-реакция обычно зависит от времени воздействия и пути воздействия (например, ингаляция, потребление с пищей); количественная оценка реакции после разного времени воздействия или для другого пути приводит к другой взаимосвязи и, возможно, другим выводам о влиянии рассматриваемого стрессора. Это ограничение вызвано сложностью биологических систем и часто неизвестными биологическими процессами, действующими между внешним воздействием и неблагоприятной клеточной или тканевой реакцией.[нужна цитата ]
Анализ Шильда
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Апрель 2019) |
Анализ Шильда может также дать представление о действии лекарств.
Смотрите также
Рекомендации
- ^ Crump, K. S .; Hoel, D.G .; Langley, C.H .; Пето, Р. (1 сентября 1976 г.). «Фундаментальные канцерогенные процессы и их значение для оценки риска низких доз». Исследования рака. 36 (9 часть 1): 2973–2979. PMID 975067.
- ^ Локхид Мартин (2009). Программное обеспечение Benchmark Dose (BMDS) Версия 2.1 Руководство пользователя Версия 2.0 (PDF) (Проект ред.). Вашингтон, округ Колумбия: Агентство по охране окружающей среды США, Управление экологической информации.
- ^ «Взаимосвязь« воздействие-реакция »- дизайн исследования, анализ данных и нормативные приложения» (PDF). 26 марта 2019.
- ^ а б c Альтшулер Б. (1981). «Моделирование зависимости доза-реакция». Перспективы гигиены окружающей среды. 42: 23–7. Дои:10.1289 / ehp.814223. ЧВК 1568781. PMID 7333256.
- ^ Гамильтон, Массачусетс; Руссо, RC; Терстон, Р.В. (1977). «Обрезанный метод Спирмена-Карбера для оценки средних летальных концентраций в биопробах токсичности». Экологические науки и технологии. 11 (7): 714–9. Bibcode:1977EnST ... 11..714H. Дои:10.1021 / es60130a004.
- ^ Бейтс, Дуглас М .; Уоттс, Дональд Г. (1988). Нелинейный регрессионный анализ и его приложения. Wiley. п. 365. ISBN 9780471816430.
- ^ Ди Вероли, Джованни Ю.; Форнари, Кьяра; Goldlust, Ян; Миллс, Грэм; Ко, Сян Бун; Bramhall, Jo L .; Richards, Frances M .; Джодрелл, Дункан И. (1 октября 2015 г.). «Автоматическая процедура подбора и программное обеспечение для кривых доза-реакция с многофазными характеристиками». Научные отчеты. 5 (1): 14701. Bibcode:2015НатСР ... 514701В. Дои:10.1038 / srep14701. ЧВК 4589737. PMID 26424192.
- ^ Neubig, Ричард Р .; Спеддинг, Майкл; Кенакин, Терри; Кристопулос, Артур; Комитет Международного союза фармакологии по номенклатуре рецепторов и классификации лекарств. (Декабрь 2003 г.). «Комитет Международного союза фармакологии по номенклатуре рецепторов и классификации лекарственных средств. XXXVIII. Обновление терминов и символов в количественной фармакологии». Фармакологические обзоры. 55 (4): 597–606. Дои:10.1124 / пр.55.4.4. PMID 14657418.
- ^ Дин, S; Sachs, F (1999). «Одноканальные свойства пуриноцепторов P2X2». J. Gen. Physiol. Издательство Рокфеллерского университета. 113 (5): 695–720. Дои:10.1085 / jgp.113.5.695. ЧВК 2222910. PMID 10228183.
- ^ Vandenberg, Laura N .; Колборн, Тео; Hayes, Tyrone B .; Heindel, Jerrold J .; Джейкобс, Дэвид Р .; Ли, Дук-Хи; Шиода, Тоши; Сото, Ана М .; vom Saal, Frederick S .; Welshons, Wade V .; Зеллер, Р. Томас; Майерс, Джон Петерсон (2012). «Гормоны и химические вещества, нарушающие работу эндокринной системы: эффекты малых доз и немонотонная доза-реакция». Эндокринные обзоры. 33 (3): 378–455. Дои:10.1210 / er.2011-1050. ЧВК 3365860. PMID 22419778.
внешняя ссылка
- Онлайн-инструмент для анализа ELISA
- Интернет IC50 Калькулятор
- Экотоксмодели Веб-сайт по математическим моделям в экотоксикологии с упором на токсикокинетико-токсикодинамические модели.
- CDD Vault, пример программного обеспечения для подбора кривой доза-реакция


![{ displaystyle { ce {[A]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/881146b6653b24508d87e34a81c84832f1d5ffea)


![{ displaystyle { frac {E} {E _ { mathrm {max}}}} = { frac {1} {1+ left ({ frac { mathrm {EC} _ {50}} {[A ]}} right) ^ {n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70e55ffd312f59c15ffc352b700ef1ab5d9fbe4c)