Галерея именованных графов - Gallery of named graphs
| На этой странице используется много изображений. Не рекомендуется просматривать эту страницу людям с медленным интернет-соединением. |
Некоторые из конечных структур, рассмотренных в теория графов имеют имена, иногда вдохновленные топологией графа, а иногда и именами первооткрывателя. Знаменитый пример - Граф Петерсена, конкретный граф с 10 вершинами, который появляется как минимальный пример или контрпример во многих различных контекстах.
Индивидуальные графики
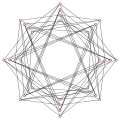
Сильно симметричные графы
Сильно регулярные графы
В сильно регулярный граф на v вершины и ранг k обычно обозначается srg (v, k, λ, μ).

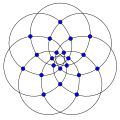
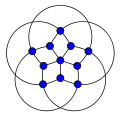
Граф Пэли порядка 13
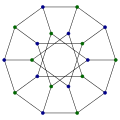
Симметричные графы
А симметричный граф тот, в котором есть симметрия (автоморфизм графа ) перевод любой упорядоченной пары смежных вершин в любую другую упорядоченную пару; то Приемная перепись перечисляет все маленькие симметричные 3-регулярные графы. Каждый сильно регулярный граф симметричен, но не наоборот.
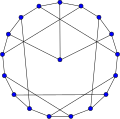
Полусимметричные графы
Семейства графов
Полные графики
В полный график на вершины часто называют -клика и обычно обозначается , с немецкого комплект.[1]
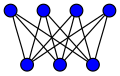
Полные двудольные графы
В полный двудольный граф обычно обозначается . За см. раздел о звездных графиках. График равен 4-тактному (квадрат), представленный ниже.


, то график полезности

Циклы
В график цикла на вершины называется n-цикл и обычно обозначается . Его также называют циклический граф, а многоугольник или н-угольник. Особые случаи треугольник , то квадрат , а затем несколько с греческими именами пятиугольник , шестиугольник , так далее.
Графики дружбы
В граф дружбы Fп может быть построен путем соединения п копии график цикла C3 с общей вершиной.[2]

Графики фуллеренов
В теории графов термин фуллерен относится к любым 3-обычный, планарный граф со всеми гранями 5 или 6 размера (включая внешнюю грань). Это следует из Формула многогранника Эйлера, V – E + F = 2 (где V, E, F указать количество вершин, ребер и граней), что в фуллерене ровно 12 пятиугольников и час = V/ 2 - 10 шестиугольников. Следовательно V = 20 + 2час; E = 30 + 3час. Графы фуллеренов - это Представления Шлегеля соответствующих фуллереновых соединений.

20-фуллерен (додекаэдр график)

24-фуллерен (Шестиугольный усеченный трапецоэдр график)
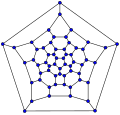
60-фуллерен (усеченный икосаэдр график)

70-фуллерен
Алгоритм генерации всех неизоморфных фуллеренов с заданным числом шестиугольных граней был разработан Г. Бринкманном и А. Дрессом.[3] Г. Бринкманн также предоставил свободно доступную реализацию под названием Fullgen.
Платоновы тела
В полный график на четырех вершинах образует каркас тетраэдр, и в более общем плане полные графы образуют скелеты симплексы. В графы гиперкуба также являются скелетами многомерных регулярных многогранники.

Куб
,
Усеченные твердые тела
Снаркс
А язвить это без моста кубический граф это требует четырех цветов в любом правильном окраска края. Самый маленький снарк - это Граф Петерсена, уже перечисленные выше.
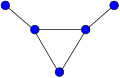
Звезда
А звезда Sk это полный двудольный граф K1,k. Звезда S3 называется когтевым графом.
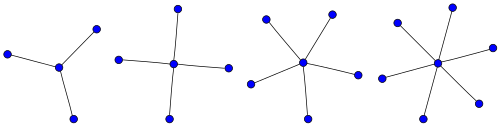
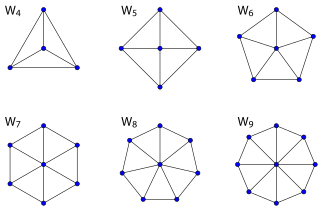
Графики колес
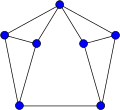
В колесо графа Wп это график на п вершины, построенные путем соединения одной вершины с каждой вершиной в (п - 1) -цикл.
Рекомендации
- ^ Дэвид Грис и Фред Б. Шнайдер, Логический подход к дискретной математике, Springer, 1993, стр. 436.
- ^ Галлиан, Дж. А. «Динамический обзор DS6: маркировка графиков». Электронный журнал комбинаторики, DS6, 1-58, 3 января 2007 г. [1] В архиве 2012-01-31 в Wayback Machine.
- ^ Бринкманн, Гуннар; Платье, Андреас В. М. (1997). «Конструктивное перечисление фуллеренов». Журнал алгоритмов. 23 (2): 345–358. Дои:10.1006 / jagm.1996.0806. МИСТЕР 1441972.