Счеты - Abacus

Для использования в других целях см. Abacus (значения).
"Abaci" и "Abacuses" перенаправляются сюда. Для турецкой фамилии см. Abacı. Для средневековой книги см. Liber Abaci.

Китайские счеты, Suanpan
Расчетный стол к Грегор Райш: Маргарита Философская, 1503. Ксилография показывает Арифметика инструктируя алгоритм и абакист (неточно представленный как Боэций и Пифагор ). Между ними возникла острая конкуренция с момента введения Алгебра в Европу в 12 веке до своего триумфа в 16 веке.[1]

В счеты (множественное число Abaci или же счеты), также называемый счетная рамка, это вычислительный инструмент, который использовался в древний Ближний Восток, Европа, Китай и Россия за столетия до принятия письменного Арабская система счисления.[1] Точное происхождение абака до сих пор неизвестно. Счеты по существу состоят из ряда рядов подвижных бусинок или других предметов, которые представляют собой цифры. Устанавливается одно из двух чисел, и бусинки управляются для реализации операции, включающей второе число (например, сложение) или, реже, квадратный или кубический корень.

Вначале ряды бусинок могли свободно лежать на плоской поверхности или скользить по канавкам. Позже бусины стали скользить по стержням, встроенным в раму, что позволило быстрее манипулировать. Счеты все еще производятся, часто как бамбук каркас с бусинами, скользящими по проволоке. В древнем мире, особенно до появления позиционная запись, счеты были практическим инструментом расчета.

Существуют отличительные современные реализации абака. Некоторые конструкции, такие как рамка для бусинок, состоящая из бусинок, разделенных на несколько десятков, используются в основном для обучения арифметика, хотя они остаются популярными в постсоветские государства как инструмент. Другой дизайн, например японский соробан, использовались для практических расчетов даже с числами, состоящими из нескольких цифр. Для любого конкретного дизайна счётов обычно существует множество различных методов выполнения вычислений, которые могут включать в себя четыре основных операции, а также квадрат и кубические корни. Некоторые из этих методов работают с не-естественный числа (числа, такие как 1.5 и ​3⁄4).

Хотя сегодня калькуляторы и компьютеры обычно используются вместо счётов, счеты по-прежнему широко используются в некоторых странах. Купцы, торговцы и служащие в некоторых частях Восточной Европы, России, Китая и Африки используют счеты, и они до сих пор используются для обучения детей арифметике.[1] Некоторые люди, которые не могут пользоваться калькулятором из-за нарушения зрения, могут использовать счеты.

Этимология

Использование слова счеты датируется до 1387 года нашей эры, когда Средний английский работа позаимствовала слово из латинский описать счёты сэндборда. Латинское слово произошло от древнегреческий ἄβαξ (abax), что означает что-то без основы и неправильно, любой кусок прямоугольной доски или доски.[2][3][4] В качестве альтернативы, без ссылки на древние тексты по этимологии, было высказано предположение, что это означает «квадратная табличка, усыпанная пылью»,[5] или «доска для рисования, покрытая пылью (для использования в математике)»[6] (точная форма латинского, возможно, отражает родительный падеж греческого слова, ἄβακoς Абакос). Хотя таблица, усыпанная пылью, популярна, некоторые не соглашаются, говоря, что это не доказано.[7][nb 1] Греческий ἄβαξ сам по себе, вероятно, является заимствованием Северо-западный семитский язык, возможно Финикийский, и родственные иврит слово Ābāq (אבק) Или «пыль» (в постбиблейском смысле означает «песок, используемый в качестве поверхности для письма»).[8]

Обе счеты[9] и Abaci[9] (мягкий или жесткий "с") используются во множественном числе. Пользователь счётов называется абакист.[10]

История

Месопотамский

В период 2700–2300 гг. До н.э. впервые появились Шумерский abacus, таблица из последовательных столбцов, в которой разграничены последовательные порядки их шестидесятеричный система счисления.[11]

Некоторые ученые указывают на персонажа в Вавилонская клинопись который мог быть получен из представления абак.[12] Это вера древневавилонян[13] такие ученые, как Карруччо, утверждали, что древние вавилоняне «могли использовать счеты для операций сложения и вычитания; однако это примитивное устройство оказалось трудным для использования для более сложных вычислений».[14]

Египтянин

Использование счётов в Древний Египет упоминается греческим историком Геродот, который пишет, что египтяне манипулировали камешками справа налево, в противоположность греческому методу слева направо. Археологи нашли древние диски различных размеров, которые, как считается, использовались в качестве счетчиков. Однако настенных изображений этого инструмента не обнаружено.[15]

Персидский

Вовремя Империя Ахеменидов Около 600 г. до н.э. персы впервые начали использовать счеты.[16] Под Парфянский, Сасанидов и Иранский империй, ученые сосредоточились на обмене знаниями и изобретениями со странами вокруг них - Индия, Китай, а Римская империя, когда считается, что его экспортировали в другие страны.

Греческий

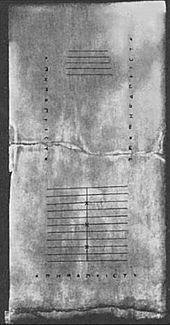
Ранняя фотография Таблички Саламина, 1899 год. Оригинал сделан из мрамора и хранится в Национальном музее эпиграфики в Афинах.

Самые ранние археологические свидетельства использования греческих счётов относятся к V веку до нашей эры.[17] Также Демосфен (384 г. до н.э. - 322 г. до н.э.) говорили о необходимости использовать гальку для вычислений, слишком сложных для вашей головы.[18][19] Игра Алексис с 4-го века до нашей эры упоминает счеты и гальку для учета, и оба Диоген и Полибий упомяните людей, которые иногда выступали за большее, а иногда за меньшее, как камешки на счетах.[19] Греческие счеты представляли собой стол из дерева или мрамора, на котором предварительно были установлены небольшие деревянные или металлические счетчики для математических расчетов. Эти греческие счеты использовались в ахеменидской Персии, этрусской цивилизации, Древнем Риме и, до Французской революции, в западном христианском мире.

Табличка, найденная на греческом острове Саламин в 1846 г. Таблетка салями ), датируется 300 годом до нашей эры, что делает ее самой старой из обнаруженных до сих пор счетных досок. Это плита из белого мрамора длиной 149 см (59 дюймов), шириной 75 см (30 дюймов) и толщиной 4,5 см (2 дюйма), на которой расположены 5 групп отметок. В центре планшета находится набор из 5 параллельных линий, поровну разделенных вертикальной линией, окаймленной полукругом на пересечении самой нижней горизонтальной линии и единственной вертикальной линии. Под этими линиями - широкое пространство с разделяющей его горизонтальной трещиной. Ниже этой трещины находится еще одна группа из одиннадцати параллельных линий, снова разделенных на две части линией, перпендикулярной им, но с полукругом в верхней части пересечения; третья, шестая и девятая из этих линий отмечены крестом в месте пересечения с вертикальной линией.[20] Также с этого периода Ваза Дария был обнаружен в 1851 году. Он был покрыт изображениями, на которых изображен "казначей", держащий в одной руке восковую табличку, а другой манипулирующий счетчиками на столе.[18]

Китайский

Основная статья: Suanpan
Китайские счеты (Suanpan ) (число, представленное на картинке - 6 302 715 408)
Счеты
Традиционный китайский算盤
Упрощенный китайский算盘
Буквальное значение"счетный лоток"

Самая ранняя известная письменная документация о китайских счетах датируется 2 веком до нашей эры.[21]

Китайские счеты, известные как Suanpan (算盤 / 算盘, букв. «Лоток для вычислений»), обычно имеет высоту 20 см (8 дюймов) и бывает разной ширины в зависимости от оператора. Обычно в нем более семи стержней. На каждом стержне верхней колоды по две бусинки, а в нижней - по пять бусинок. Бусины обычно округлые и сделаны из твердая древесина. Подсчет бусинок осуществляется перемещением их вверх или вниз по направлению к лучу; бусинки, переместившиеся к лучу, подсчитываются, а отодвинутые - нет.[22] Одна из верхних бусинок - 5, а одна из нижних - 1. Под каждым стержнем стоит число, показывающее разряд. Suanpan можно мгновенно вернуть в исходное положение быстрым движением по горизонтальной оси, чтобы повернуть все бусинки от горизонтального луча в центре.

Прототип китайских счётов появился во время династия Хан, а бусинки овальные. В Династия Сун и ранее использовали счеты типа 1: 4 или счеты с четырьмя бусинами, похожие на современные счеты, включая форму бусинок, обычно известных как счеты в японском стиле.[нужна цитата ]

Рано Династия Мин, счеты стали появляться в виде счётов 1: 5. Верхняя дека имела одну бусину, а нижняя - пять бус.[нужна цитата ]

В конце династии Мин стиль абака появился в форме 2: 5.[нужна цитата ] На верхней колоде было две бусинки, а на нижней - пять.

Были разработаны различные методы расчета Suanpan возможность эффективных расчетов. В настоящее время существуют школы, обучающие студентов тому, как им пользоваться.

В длинном свитке Вдоль реки во время фестиваля Цинмин нарисовано Чжан Цзэдуань вовремя Династия Сун (960–1297), а Suanpan хорошо видна рядом с бухгалтерской книгой и рецептами врача на прилавке аптекарь (Фейбао).

Сходство Римские счеты китайцам один предполагает, что один мог вдохновить другого, поскольку есть некоторые свидетельства торговых отношений между Римская империя и Китай. Однако никакой прямой связи показать нельзя, и сходство счет может быть случайным, поскольку оба в конечном итоге возникают из-за счета пятью пальцами на руке. Где римская модель (как и большинство современных корейских и Японский ) имеет 4 плюс 1 бусину на десятичный знак, стандартный Suanpan имеет 5 плюс 2. Это, кстати, позволяет использовать с шестнадцатеричный система счисления (или любая основание до 18), которые могли использоваться для традиционных китайских мер веса. (Вместо того, чтобы двигаться по проводам, как в китайской, корейской и японской моделях, бусинки римской модели проходят по канавкам, по-видимому, значительно замедляя арифметические вычисления.

Другой возможный источник Suanpan китайский счетные стержни, который работал с десятичная система но не хватало концепции нуль как заполнитель. Ноль, вероятно, был представлен китайцам в Династия Тан (618–907) при путешествии в Индийский океан и Средний Восток обеспечил бы прямой контакт с Индия, позволяя им усвоить понятие нуля и десятичная точка у индийских купцов и математиков.

Римский

Основная статья: Римские счеты
Копия Римские счеты

Обычный метод расчета в Древнем Риме, как и в Греции, заключался в перемещении счетчиков на гладком столе. Первоначально галька (исчисления) были использованы. Позже и в средневековой Европе жетоны были изготовлены. Отмеченными линиями указаны единицы, пятерки, десятки и т. Д., Как в Римская цифра система. Эта система «встречного литья» продолжалась в поздней Римской империи и в средневековой Европе и сохранялась в ограниченном использовании до девятнадцатого века.[23] Из-за Папа Сильвестр II повторное введение счётов с модификациями, они снова стали широко использоваться в Европе в 11 веке.[24][25] В этих счетах использовались бусины на проводах, в отличие от традиционных римских счетных досок, что означало, что счеты можно было использовать намного быстрее.[26]

Написанный в I веке до нашей эры, Гораций ссылается на восковые счеты, доску, покрытую тонким слоем черного воска, на которой с помощью стилуса были начертаны колонны и фигуры.[27]

Один из примеров археологических свидетельств Римские счеты Показанная здесь реконструкция, датируется I веком нашей эры. Он имеет восемь длинных канавок, содержащих до пяти бусинок в каждой, и восемь более коротких бороздок, в каждой из которых либо по одной бусинке, либо нет. Канавка с отметкой I указывает единицы, X десятков и так далее до миллионов. Бусинки в более коротких канавках обозначают пятерки - пять единиц, пять десятков и т. Д., В основном в двоично-десятичный кодированный десятичный система, относящаяся к римские цифры. Короткие бороздки справа могли использоваться для обозначения римских «унций» (т.е. дробей).

Индийский

В Абхидхармакошабхашья из Васубандху (316-396), санскритский труд по буддийской философии, говорит, что философ II века н.э. Васумитра сказал, что "поместив фитиль (санскрит вартика) на номер один (ekāṅka) означает, что это единица, в то время как размещение фитиля на цифре сотня означает, что она называется сотней, а на цифре тысяча означает, что это тысяча ». Неясно, что именно могло быть это расположение. Примерно в 5 веке , Индийские клерки уже находили новые способы записи содержимого Abacus.[28] В индуистских текстах используется термин шунья (ноль) для обозначения пустого столбца на счетах.[29]

Японский

Основная статья: Соробан
Японский соробан

По-японски счеты называются соробан (算盤, そ ろ ば ん, лит. «Счетный лоток»), привезенный из Китая в XIV веке.[30] Вероятно, он использовался рабочим классом за столетие или более до того, как появился правящий класс, поскольку классовая структура не позволяла устройствам, используемым более низким классом, быть адаптированными или использоваться правящим классом.[31] Счеты 1/4, которые удаляют редко используемые вторую и пятую бусинки, стали популярными в 1940-х годах.

Сегодняшние японские счеты относятся к типу 1: 4, счеты с четырьмя бусинами были завезены из Китая в эпоху Муромати. Он принимает форму одной бусинки верхней деки и четырех нижних бусинок. Верхняя бусина на верхней деке была равна пяти, а нижняя равнялась единице, как на китайских или корейских счетах, а десятичное число может быть выражено, поэтому счеты выполнены в виде одного четырех счеты. Бусины всегда имеют форму ромба. Вместо метода деления обычно используется частное деление; в то же время, для того, чтобы цифры умножения и деления были единообразными, используют умножение делением. Позже в Японии появились счеты 3: 5 под названием 天 三 算盤, которые сейчас находятся в коллекции Изэ Ронгджи в деревне Шаньси в Ямагата Город. Были также счеты типа 2: 5.

Поскольку счеты с четырьмя бусинами распространены, японские счеты также широко используются во всем мире. Также в разных местах есть улучшенные японские счеты. Счеты японского производства, сделанные в Китае, представляют собой счеты с пластиковыми бусинами в алюминиевой рамке. Напильник стоит рядом с четырьмя бусинками и кнопкой «очистки», нажимаем кнопку очистки, сразу ставим верхнюю бусину в верхнее положение, нижнюю бусину набираем в нижнее положение, сразу очищается, проста в использовании.

Счеты по-прежнему производятся в Японии, даже несмотря на их широкое распространение, практичность и доступность по цене. электронные калькуляторы. Использование соробана до сих пор преподается на японском языке. начальные школы как часть математика, в первую очередь как помощь в более быстром умственном вычислении. Используя визуальные образы соробана, можно прийти к ответу за то же время, или даже быстрее, чем это возможно с физическим инструментом.[32]

Корейский

Китайские счеты перекочевали из Китая в Корея около 1400 г. н.э.[18][33][34] Корейцы называют это Jupan (주판), супан (수판) или Джусан (주산).[35]Счеты с четырьмя бусинками (1: 4) были представлены корейской династии Корё из Китая во время династии Сун, позже счеты с пятью бусинами (5: 1) были представлены корейцам из Китая во время династии Мин.

Коренной американец

Представление Инки кипу
А юпана как использовали инки.

В некоторых источниках упоминается использование абака, называемого непохуальцинцин в древности Ацтеков культура.[36] В этих мезоамериканских счетах использовалась пятизначная система с основанием 20.[37]Слово Nephualtzintzin [nepoːwaɬˈt͡sint͡sin] происходит от Науатль и он образован корнями; Ne - личные -; pōhual или же Pōhualli [ˈPoːwalːi] - счет -; и Цинцин [ˈT͡sint͡sin] - мелкие похожие элементы. Его полное значение было понято как: подсчет кем-то с небольшими похожими элементами. Его использованию учили в Calmecac к Temalpouhqueh [temaɬˈpoʍkeʔ], которые с детства были учениками, посвятившими себя учету небес.

Непухуальцинцин был разделен на две основные части, разделенные перемычкой или промежуточным шнуром. В левой части было четыре бусинки, которые в первом ряду имеют единичные значения (1, 2, 3 и 4), а в правой части - три бусины со значениями 5, 10 и 15 соответственно. Для того, чтобы узнать стоимость соответствующих бусинок верхних рядов, достаточно умножить на 20 (по каждой строке) значение соответствующего счета в первой строке.

Всего было 13 рядов по 7 бусинок в каждом, что составляло 91 бусину в каждом непуальцинцин. Это было основное число, которое нужно было понять, 7 умноженное на 13, тесную связь между природными явлениями, подземным миром и небесными циклами. Один непуальцицин (91) представляет количество дней, которые длится сезон в году, два непуальцицина (182) - это количество дней цикла кукурузы от посева до сбора урожая, три непуальцинцин (273) - количество дней. беременности ребенка, а четыре непуальцинцинца (364) завершили цикл и приблизительно год (11/4 дней меньше). При переводе на современную компьютерную арифметику Непухуальцинцин занял с 10 по 18 место в рейтинге. плавающая точка, который рассчитывал как звездные, так и бесконечно малые величины с абсолютной точностью, означал, что округление не допускается.

Повторное открытие Nepōhualtzintzin произошло благодаря мексиканскому инженеру Дэвиду Эспарса Идальго,[38] который во время своих странствий по Мексике обнаружил разнообразные гравюры и изображения этого инструмента и реконструировал некоторые из них, сделанные из золота, нефрита, инкрустации ракушками и т. д.[39] Также были найдены очень старые непуальцинцинцы, приписываемые Ольмек культуры, и даже некоторые браслеты майя происхождение, а также разнообразие форм и материалов в других культурах.

Джордж И. Санчес, "Арифметика в майя", Остин, штат Техас, 1961, обнаружил еще одно счеты по основанию 5 и 4 в Полуостров Юкатан которые также вычисляли данные календаря. Это были пальцевые счеты, с одной стороны использовались 0, 1, 2, 3 и 4; а с другой стороны использовались 0, 1, 2 и 3. Обратите внимание на использование нуля в начале и в конце двух циклов. Санчес работал с Сильванус Морли, известный майянист.

В кипу из Инки была система цветных узловатых шнуров, используемых для записи числовых данных,[40] как продвинутый подсчетные палочки - но не используется для расчетов. Расчеты проводились с использованием юпана (кечуа для «счетного инструмента»; см. рисунок), который все еще использовался после завоевания Перу. Принцип работы юпаны неизвестен, но в 2001 году объяснение математической основы этих инструментов было предложено итальянским математиком Николино де Паскуале. Сравнивая форму нескольких юпанов, исследователи обнаружили, что расчеты проводились с использованием Последовательность Фибоначчи 1, 1, 2, 3, 5 и степени 10, 20 и 40 в качестве значений разряда для различных полей в приборе. Использование последовательности Фибоначчи позволит свести к минимуму количество зерен в любом одном поле.[41]

русский

Русские счеты

Русские счеты, щотый (русский: счёты, множественное число от русский: счёт, считая), как правило, имеет одну наклонную колоду с десятью бусинами на каждой проволоке (за исключением одной проволоки, обычно расположенной рядом с пользователем, с четырьмя бусинами для долей в четверть рубля). Старые модели имеют еще одну 4-х бортовую проволоку для четверти длины.копейки, которые чеканились до 1916 года. Русские счеты часто используют вертикально, с каждой проволокой слева направо, как строчки в книге. Проволока обычно изогнута, чтобы выступать вверх в центре, чтобы бусины были прикреплены к любой из двух сторон. Он очищается, когда все бусинки сдвигаются вправо. Во время манипуляции бусинки перемещают влево. Для удобства просмотра две средние бусины на каждой проволоке (5-я и 6-я бусинки) обычно имеют цвет, отличный от цвета остальных восьми бусинок. Точно так же левая полоса проволоки тысяч (и проволоки миллиона, если она есть) может иметь другой цвет.

Российские счеты как простое, дешевое и надежное устройство использовались во всех магазинах и на рынках по всей стране. бывший Советский Союз, и его использование преподавалось в большинстве школ до 1990-х годов.[42][43] Даже изобретение 1874 года механический калькулятор, Арифмометр Однера, не заменил их в Россия; в соответствии с Яков Перельман Известно, что даже в его время некоторые бизнесмены, пытавшиеся завезти такие устройства в Российскую империю, сдались и ушли в отчаянии, когда им показали работу опытного оператора счёта.[44] Точно так же массовое производство арифмометров Феликса с 1924 г. не привело к значительному сокращению их использования в Советский союз.[45] Русские счеты начали терять популярность только после массового производства микрокалькуляторы началось в Советском Союзе в 1974 году. Сегодня это считается архаизмом и заменено портативным калькулятором.

Русские счеты были привезены во Францию ​​около 1820 года математиком. Жан-Виктор Понселе, который служил в Наполеон русской армии и был военнопленным в России.[46] Счеты вышли из употребления в Западной Европе в 16 веке с появлением десятичной системы счисления и алгоритмический методы. Для французских современников Понселе это было чем-то новым. Понселе использовал его не для каких-либо прикладных целей, а как обучающее и демонстрационное средство.[47] В Турки и Армянский люди тоже пользовались счетами, похожими на российские щоты. Он был назван кулба турками и хореб армянами.[48]

Школьные счеты

Счеты начала 20 века, используемые в датской начальной школе.
Двадцать бусина Рекенрек

Во всем мире счеты использовались в дошкольных и начальных школах в качестве вспомогательного средства при обучении система счисления и арифметика.

В западных странах широко распространена бусинка, похожая на российские счеты, но с прямыми проволоками и вертикальной рамкой (см. Изображение). Его до сих пор часто считают пластиковой или деревянной игрушкой.

Каркас может использоваться либо с позиционным обозначением, как и другие счеты (таким образом, 10-проводная версия может представлять числа до 9 999 999 999), или каждая полоса может представлять одну единицу (так, например, 74 может быть представлено смещением всех бусинок на 7 проволоках. и 4 бисеринки на 8-й проволоке, так что числа могут быть до 100). В показанной рамке для бортов зазор между 5-й и 6-й проволокой, соответствующий изменению цвета между 5-й и 6-й бисериной на каждой проволоке, предполагает использование последнего. Обучение умножению, например 6 раз по 7 можно изобразить смещением 7 бусинок на 6 проволок.

Красно-белые счеты используются в современных начальных школах для большого количества уроков, связанных с числами. Версия с двадцатью бусинами, называемая нидерландский язык имя Рекенрек («расчетный каркас»), часто используется, иногда на бусинах, иногда на жестком каркасе.[49]

Скорость

Выдающийся физик Ричард Фейнман был отмечен за опыт в математических расчетах. Он написал о встрече в Бразилии с японским экспертом по счетам, который бросил ему вызов в соревнованиях по скорости между ручкой и бумагой Фейнмана и счетами. Счеты были намного быстрее для сложения, несколько быстрее для умножения, но Фейнман был быстрее при делении. Когда счеты использовались для действительно сложной задачи, кубических корней, Фейнман выигрывал легко, но по счастливой случайности, поскольку число, выбранное наугад, было близко к числу, которое Фейнман знал, что это точный куб, что позволяет использовать приближенные методы.[50]

Неврологический анализ

Научившись считать на счетах, можно улучшить свой умственный расчет, который становится быстрее и точнее при выполнении вычислений с большими числами. Мысленный расчет на основе абака (AMC) был получен от абака, что означает выполнение вычислений, включая сложение, вычитание, умножение и деление, в уме с воображаемыми счетами. Это когнитивный навык высокого уровня, который позволяет выполнять вычисления с помощью эффективного алгоритма. Люди, проходящие длительное обучение AMC, демонстрируют более высокий объем числовой памяти и более эффективно связаны между собой нервными путями.[51][52] Они могут извлекать память для сложных вычислений.[53] Обработка AMC включает как зрительно-пространственный и зрительно-моторную обработку, которая генерирует визуальные счеты и выполняет движение воображаемой бусинки.[54] Поскольку единственное, что нужно запомнить, это конечное положение бусинок, это требует меньше памяти и меньше времени на вычисления.[54]

Галерея счётов эпохи Возрождения

  • Грегор Райш, Margarita Philosophica, 1508 (1230x1615) .png
  • Rechentisch.png
  • Rechnung auff der Linihen und Federn.JPG
  • Köbel Böschenteyn 1514.jpg
  • Rechnung auff der linihen 1525 Adam Ries.PNG
  • 1543 Роберт Рекорд.PNG
  • Питер Апиан 1544.PNG
  • Адам Ризен.jpg
  • Рекенаар 1553.jpg

Бинарные счеты

Две бинарные счеты, построенные доктором Робертом К. Гудом-младшим из двух китайских счётов.

Двоичные счеты используются для объяснения того, как компьютеры манипулируют числами.[55] Счеты показывают, как числа, буквы и знаки могут храниться в бинарная система на компьютере или через ASCII. Устройство состоит из ряда бусинок на параллельных проводах, расположенных в три отдельных ряда. Бусины представляют собой переключатель на компьютере в положении «включено» или «выключено».

Использование слепыми людьми

Адаптированные счеты, изобретенные Тимом Кранмером, называются Cranmer abacus до сих пор широко используется людьми, которые слепой. За бортами кладут кусок мягкой ткани или резины, чтобы они случайно не сдвинулись. Это удерживает бусинки на месте, пока пользователи их ощущают или манипулируют. Они используют счеты для выполнения математических функций. умножение, разделение, добавление, вычитание, квадратный корень и кубический корень.[56]

Хотя слепые учащиеся пользуются говорящими калькуляторами, этих учащихся в начальных классах по-прежнему очень часто обучают счетам, как в государственных школах, так и в государственных школах для слепых.[57] Слепые ученики также выполняют математические задания, используя шрифт Брайля и Код Немет (тип кода Брайля для математики), но большое умножение и длинное деление проблемы могут быть долгими и трудными. Счеты дают слепым и слабовидящим ученикам инструмент для решения математических задач, который соответствует скорости и математическим знаниям, необходимым их зрячим сверстникам, использующим карандаш и бумагу. Многие слепые люди считают эту числовую машину очень полезным инструментом на протяжении всей жизни.[56]

Смотрите также

Примечания

  1. ^ И К. Дж. Гадд, хранитель египетских и ассирийских древностей в британский музей, и Джейкоб Леви, еврейский историк, писавший Neuhebräisches und chaldäisches wörterbuch über die Talmudim und Midraschim [Neuhebräisches и халдейский словарь по Талмудам и мидраши] не согласен с теорией "пылевого стола".[7]

Сноски

  1. ^ а б c Бойер и Мерцбах 1991, стр. 252–253
  2. ^ де Стефани 1909, п. 2
  3. ^ Гайсфорд 1962, п. 2
  4. ^ Лассер и Ливадарас 1976, п. 4
  5. ^ Кляйн 1966, п. 1
  6. ^ Лук, Фридрихсен и Берчфилд 1967, п. 2
  7. ^ а б Пуллан 1968, п. 17
  8. ^ Huehnergard 2011, п. 2
  9. ^ а б Коричневый 1993, п. 2
  10. ^ Правительство 1976, п. 1
  11. ^ Ифрах 2001, п. 11
  12. ^ Crump 1992, п. 188
  13. ^ Мелвилл 2001
  14. ^ Карруччо 2006, п. 14
  15. ^ Смит 1958, стр. 157–160
  16. ^ Карр 2014
  17. ^ Ифрах 2001, п. 15
  18. ^ а б c Уильямс 1997, п. 55
  19. ^ а б Пуллан 1968, п. 16
  20. ^ Уильямс 1997, стр. 55–56
  21. ^ Ифрах 2001, п. 17
  22. ^ Фернандес 2003
  23. ^ Пуллан 1968, п. 18
  24. ^ Коричневый 2010, стр. 81–82
  25. ^ Коричневый 2011
  26. ^ Хафф 1993, п. 50
  27. ^ Ифрах 2001, п. 18
  28. ^ Кёрнер 1996, п. 232
  29. ^ Моллин 1998, п. 3
  30. ^ Гуллберг 1997, п. 169
  31. ^ Уильямс 1997, п. 65
  32. ^ Мюррей 1982
  33. ^ Анон 2002
  34. ^ Джами 1998, п. 4
  35. ^ Анон 2013
  36. ^ Саньял 2008
  37. ^ Анон 2004
  38. ^ Идальго 1977, п. 94
  39. ^ Идальго 1977, стр. 94–101
  40. ^ Альбри 2000, п. 42
  41. ^ Эми и Де Паскуале 2005
  42. ^ Бернетт и Райан 1998, п. 7
  43. ^ Хаджинс 2004, п. 219
  44. ^ Арифметика для развлечений, Яков Перельман, стр. 51.
  45. ^ Леушина 1991, п. 427
  46. ^ Трогеман и Эрнст 2001, п. 24
  47. ^ Флегг 1983, п. 72
  48. ^ Уильямс 1997, п. 64
  49. ^ Запад 2011, п. 49
  50. ^ Фейнман, Ричард (1985). «Счастливые числа». Вы, конечно, шутите, мистер Фейнман!. Нью-Йорк: W.W. Нортон. ISBN  0-393-31604-1. OCLC  10925248.
  51. ^ Ху, Юйчжэн; Гэн, Фэнцзи; Тао, Ликсия; Ху, Нанту; Du, Fenglei; Фу, Куанг; Чен, Фэйянь (14 декабря 2010 г.). «Улучшенная целостность трактов белого вещества у детей с обучением счетам». Картирование человеческого мозга. 32 (1): 10–21. Дои:10.1002 / hbm.20996. ISSN  1065-9471. ЧВК  6870462. PMID  20235096.
  52. ^ Ву, Дун-Синь; Чен, Чиа-Линь; Хуанг, Юнг-Хуэй; Лю, Жэнь-Шянь; Се, Джен-Чуэн; Ли, Джейсон Дж. С. (5 ноября 2008 г.). «Влияние длительной практики и сложности задачи на деятельность мозга при выполнении мысленных вычислений на основе счётов: исследование ПЭТ». Европейский журнал ядерной медицины и молекулярной визуализации. 36 (3): 436–445. Дои:10.1007 / s00259-008-0949-0. ISSN  1619-7070. PMID  18985348. S2CID  9860036.
  53. ^ Lee, J.S .; Chen, C.L .; Wu, T.H .; Hsieh, J.C .; Wui, Y.T .; Cheng, M.C .; Хуанг, Ю. (2003). «Активация мозга во время ментальных вычислений на основе счётов с помощью фМРТ: сравнение экспертов по счётам и нормальных субъектов». Первая международная конференция IEEE EMBS по нейронной инженерии, 2003 г. Материалы конференции. С. 553–556. Дои:10.1109 / CNE.2003.1196886. ISBN  0-7803-7579-3. S2CID  60704352.
  54. ^ а б Chen, C.L .; Wu, T.H .; Cheng, M.C .; Huang, Y.H .; Sheu, C.Y .; Hsieh, J.C .; Ли, Дж. (20 декабря 2006 г.). «Проспективная демонстрация пластичности мозга после интенсивной тренировки мысленных вычислений на основе абака: исследование фМРТ». Ядерные инструменты и методы в физических исследованиях Секция A: ускорители, спектрометры, детекторы и связанное с ними оборудование. 569 (2): 567–571. Bibcode:2006NIMPA.569..567C. Дои:10.1016 / j.nima.2006.08.101. ISSN  0168-9002.
  55. ^ Хороший младший 1985, п. 34
  56. ^ а б Терлау и Гиссони 2006
  57. ^ Пресли и Д'Андреа 2009

Рекомендации

  • Айми, Антонио; Де Паскуале, Николино (2005). «Андские калькуляторы» (PDF). перевод Дель Бьянко, Franca. В архиве (PDF) из оригинала 3 мая 2015 г.. Получено 31 июля, 2014.CS1 maint: ref = harv (связь)
  • Альбри, Джо (2000). Гессенбрух, Арне (ред.). Справочник по истории науки. Лондон, Великобритания: Fitzroy Dearborn Publishers. ISBN  978-1-884964-29-9.CS1 maint: ref = harv (связь)
  • Анон (12 сентября 2002 г.). «Средневековье Abacus, регион происхождения Ближний Восток». История вычислительного проекта. В архиве из оригинала 9 мая 2014 г.. Получено 31 июля, 2014.CS1 maint: ref = harv (связь)
  • Анон (2004). "Nepohualtzintzin, Доиспанский компьютер". Иберамия 2004. В архиве из оригинала 3 мая 2015 г.. Получено 31 июля, 2014.CS1 maint: ref = harv (связь)
  • Анон (2013). 주판 [Счеты]. enc.daum.net (на корейском). В архиве из оригинала 7 июля 2012 г.. Получено 31 июля, 2014.CS1 maint: ref = harv (связь)
  • Бойер, Карл Б .; Мерцбах, Ута К. (1991). История математики (2-е изд.). John Wiley & Sons, Inc. ISBN  978-0-471-54397-8.CS1 maint: ref = harv (связь)
  • Браун, Лесли, изд. (1993). "счеты". Краткий оксфордский словарь английского языка по историческим принципам. 2: A-K (5-е изд.). Оксфорд, Великобритания: Издательство Оксфордского университета. ISBN  978-0-19-860575-1.CS1 maint: ref = harv (связь)
  • Браун, Нэнси Мари (2010). Счеты и крест: история Папы, который принес свет науки в темные века. Филадельфия, Пенсильвания: Основные книги. ISBN  978-0-465-00950-3.CS1 maint: ref = harv (связь)
  • Браун, Нэнси Мари (2 января 2011 г.). «Все, что вы думаете, что знаете о темных веках, неверно». rd журнал (Опрос). USC Annenberg. В архиве из оригинала от 8 августа 2014 г.CS1 maint: ref = harv (связь)
  • Бернетт, Чарльз; Райан, В. Ф. (1998). «Абакус (западный)». In Bud, Роберт; Уорнер, Дебора Джин (ред.). Инструменты науки: историческая энциклопедия. Энциклопедии Гарленд в истории науки. Нью-Йорк, штат Нью-Йорк: Garland Publishing, Inc., стр. 5–7. ISBN  978-0-8153-1561-2.CS1 maint: ref = harv (связь)
  • Карр, Карен (2014). «Западноазиатская математика». Kidipede. История для детей !. Архивировано из оригинал 3 июля 2014 г.. Получено 19 июня, 2014.CS1 maint: ref = harv (связь)
  • Карруччо, Этторе (2006). Математика и логика в истории и современной мысли. перевод Квигли, Изабель. Алдин Транзакция. ISBN  978-0-202-30850-0.CS1 maint: ref = harv (связь)
  • Крамп, Томас (1992). Японская игра в числа: использование и понимание чисел в современной Японии. Серия японских исследований Института Ниссана / Рутледж. Рутледж. ISBN  978-0-415-05609-0.CS1 maint: ref = harv (связь)
  • де Стефани, Алоизиус, изд. (1909). Etymologicum Gudianum quod vocatur; Recensuit et apparatum criticalum indicesque adiecit. я. Лейпциг, Германия: Teubner. LCCN  23016143.CS1 maint: ref = harv (связь)
  • Фернандес, Луис (27 ноября 2003 г.). "Краткое введение в Abacus". ee.ryerson.ca. Архивировано из оригинал 26 декабря 2014 г.. Получено 31 июля, 2014.CS1 maint: ref = harv (связь)
  • Флегг, Грэм (1983). Числа: их история и значение. Дуврские книги по математике. Минеола, Нью-Йорк: Courier Dover Publications. ISBN  978-0-233-97516-0.CS1 maint: ref = harv (связь)
  • Гайсфорд, Томас, изд. (1962) [1848]. Etymologicon Magnum seu verius Lexicon Saepissime vocabulorum origines indagans ex pluribus lexicis scholiastis et grammaticis anonymi cuiusdam opera concinnatum [Великий этимологикон: который содержит происхождение лексикона слов из большого числа или, скорее, из большого количества исследований Lexicis Scholiastis и связанных между собой работами анонимных грамматиков] (на латыни). Амстердам, Нидерланды: Адольф М. Хаккерт.CS1 maint: ref = harv (связь)
  • Гуд-младший, Роберт К. (осень 1985 г.). «Двоичные счеты: полезный инструмент для объяснения компьютерных операций». Журнал "Компьютеры в математике и преподавании естественных наук". 5 (1): 34–37.CS1 maint: ref = harv (связь)
  • Гоув, Филип Бэбкок, изд. (1976). "абакист". Третий новый международный словарь Вебстера (17-е изд.). Спрингфилд, Массачусетс: Компания G. & C. Merriam. ISBN  978-0-87779-101-0.CS1 maint: ref = harv (связь)
  • Гуллберг, Ян (1997). Математика: от рождения чисел. Иллюстрировано Пэром Гуллбергом. Нью-Йорк, штат Нью-Йорк: W. W. Norton & Company. ISBN  978-0-393-04002-9.CS1 maint: ref = harv (связь)
  • Идальго, Дэвид Эспарза (1977). Nepohualtzintzin: Computador Prehispánico en Vigencia [Непохуальцинцин: эффективный доиспанский компьютер] (на испанском). Тлакокемекатль, Мексика: Редакция Диана.CS1 maint: ref = harv (связь)
  • Хаджинс, Шарон (2004). Другая сторона России: кусочек жизни в Сибири и на Дальнем Востоке. Евгения и Хью М. Стюарт Серия 26 о Восточной Европе. Издательство Техасского университета A&M. ISBN  978-1-58544-404-5.CS1 maint: ref = harv (связь)
  • Huehnergard, Джон, изд. (2011). "Приложение семитских корней, под корень ʾBq.". Словарь английского языка American Heritage (5-е изд.). Houghton Mifflin Harcourt Trade. ISBN  978-0-547-04101-8.CS1 maint: ref = harv (связь)
  • Хафф, Тоби Э. (1993). Расцвет ранней современной науки: ислам, Китай и Запад (1-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-43496-6.CS1 maint: ref = harv (связь)
  • Ифра, Жорж (2001). Универсальная история вычислительной техники: от абак до квантового компьютера. Нью-Йорк, штат Нью-Йорк: John Wiley & Sons, Inc. ISBN  978-0-471-39671-0.CS1 maint: ref = harv (связь)
  • Джами, Екатерина (1998). «Абакус (Восточный)». In Bud, Роберт; Уорнер, Дебора Джин (ред.). Инструменты науки: историческая энциклопедия. Нью-Йорк, штат Нью-Йорк: Garland Publishing, Inc. ISBN  978-0-8153-1561-2.CS1 maint: ref = harv (связь)
  • Кляйн, Эрнест, изд. (1966). "счеты". Большой этимологический словарь английского языка. Я: А-К. Амстердам: Издательство Elsevier.CS1 maint: ref = harv (связь)
  • Кёрнер, Томас Уильям (1996). Удовольствие от счета. Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  978-0-521-56823-4.CS1 maint: ref = harv (связь)
  • Лассер, Франциск; Ливадарас, Николай, ред. (1976). Etymologicum Magnum Genuinum: Symeonis Etymologicum: Una Cum Magna Grammatica (на греческом и латинском языках). Примум: α - άμωσϒέπωϛ. Рим, Италия: Edizioni dell'Ateneo. LCCN  77467964.CS1 maint: ref = harv (связь)
  • Леушина, А. М. (1991). Развитие элементарных математических представлений у дошкольников. Национальный совет учителей математики. ISBN  978-0-87353-299-0.CS1 maint: ref = harv (связь)
  • Мелвилл, Дункан Дж. (30 мая 2001 г.). «Хронология месопотамской математики». Университет Святого Лаврентия. It.stlawu.edu. В архиве из оригинала 12 января 2014 г.. Получено 19 июня, 2014.CS1 maint: ref = harv (связь)
  • Миш, Фредерик С., изд. (2003). "счеты". Энциклопедический словарь Мерриам-Вебстера (11-е изд.). Merriam-Webster, Inc. ISBN  978-0-87779-809-5.
  • Моллин, Ричард Энтони (сентябрь 1998 г.). Фундаментальная теория чисел с приложениями. Дискретная математика и ее приложения. Бока-Ратон, Флорида: CRC Press. ISBN  978-0-8493-3987-5.CS1 maint: ref = harv (связь)
  • Мюррей, Джеффри (20 июля 1982 г.). "Древний калькулятор стал хитом нового поколения Японии". The Christian Science Monitor. CSMonitor.com. В архиве с оригинала 2 декабря 2013 г.. Получено 31 июля, 2014.CS1 maint: ref = harv (связь)
  • Лук, C. T .; Friedrichsen, G.W.S .; Берчфилд, Р. У., ред. (1967). "счеты". Оксфордский словарь этимологии английского языка. Оксфорд, Великобритания: Оксфорд в Clarendon Press.CS1 maint: ref = harv (связь)
  • Пресли, Айк; Д'Андреа, Фрэнсис Мэри (2009). Вспомогательные технологии для слепых или слабовидящих студентов: руководство по оценке. Американский фонд слепых. п. 61. ISBN  978-0-89128-890-9.CS1 maint: ref = harv (связь)
  • Пуллан, Дж. М. (1968). История Abacus. Нью-Йорк, штат Нью-Йорк: Frederick A. Praeger, Inc., Publishers. ISBN  978-0-09-089410-9. LCCN  72075113.CS1 maint: ref = harv (связь)
  • Рейли, Эдвин Д., изд. (2004). Краткая энциклопедия компьютерных наук. Нью-Йорк, штат Нью-Йорк: John Wiley and Sons, Inc. ISBN  978-0-470-09095-4.
  • Саньял, Амитава (6 июля 2008 г.). «Учимся бусам». Hindustan Times.CS1 maint: ref = harv (связь)
  • Смит, Дэвид Юджин (1958). История математики. Дуврские книги по математике. 2: Специальные разделы элементарной математики. Courier Dover Publications. ISBN  978-0-486-20430-7.CS1 maint: ref = harv (связь)
  • Стернс, Питер Н .; Лангер, Уильям Леонард, ред. (2001). «Энциклопедия всемирной истории: древняя, средневековая и современная, в хронологическом порядке». Энциклопедия всемирной истории (6-е изд.). Нью-Йорк, Нью-Йорк: Houghton Mifflin Harcourt. ISBN  978-0-395-65237-4.
  • Терлау, Терри; Гиссони, Фред (март 2005 г.). "APH News, март 2005 г .: Abacus = карандаш и бумага при расчетах". APH.org. В архиве из оригинала от 2 декабря 2013 г.CS1 maint: ref = harv (связь)
  • Трогеман, Георг; Эрнст, Вольфганг (2001). Трогеман, Георг; Нитусов, Александр Юрьевич .; Эрнст, Вольфганг (ред.). Вычислительная техника в России: раскрыта история компьютерных устройств и информационных технологий. Брауншвейг / Висбаден: Vieweg + Teubner Verlag. ISBN  978-3-528-05757-2.CS1 maint: ref = harv (связь)
  • Запад, Джессика Ф. (2011). Распознавание чисел: ежедневное развитие числовой грамотности в классах K-3. Портленд, я: Издательство Stenhouse. ISBN  978-1-57110-790-9.CS1 maint: ref = harv (связь)
  • Уильямс, Майкл Р. (1997). Балтес, Шерил (ред.). История вычислительной техники (2-е изд.). Лос-Аламитос, Калифорния: Пресса компьютерного общества IEEE. ISBN  978-0-8186-7739-7. LCCN  96045232.CS1 maint: ref = harv (связь)
  • Хомут, Хо Пэн (2000). Ли, Ци и Шу: введение в науку и цивилизацию Китая. Dover Science Books. Courier Dover Publications. ISBN  978-0-486-41445-4.

Чтение

  • Фернандес, Луис (2013). "Счеты: краткая история". ee.ryerson.ca. В архиве из оригинала 2 июля 2014 г.. Получено 31 июля, 2014.CS1 maint: ref = harv (связь)
  • Меннингер, Карл В. (1969), Числовые слова и числовые символы: культурная история чисел, MIT Press, ISBN  978-0-262-13040-0
  • Кодзима, Такаши (1954), Японские счеты: их использование и теория, Токио: Charles E. Tuttle Co., Inc., ISBN  978-0-8048-0278-9
  • Кодзима, Такаши (1963), Advanced Abacus: японская теория и практика, Токио: Charles E. Tuttle Co., Inc., ISBN  978-0-8048-0003-7
  • Стивенсон, Стивен Кент (7 июля 2010 г.), Древние компьютеры, Сеть глобальной истории IEEE, arXiv:1206.4349, Bibcode:2012arXiv1206.4349S, получено 2 июля, 2011
  • Стивенсон, Стивен Кент (2013), Древние компьютеры, часть I - Повторное открытие (2-е изд.), ISBN  978-1-4909-6437-9

внешняя ссылка

Учебники

Abacus curiosities