Дискретное исчисление - Discrete calculus

Дискретное исчисление или исчисление дискретных функций, это математический исследование добавочный изменить так же, как геометрия это изучение формы и алгебра изучение обобщений арифметические операции. Слово исчисление это латинский слово, изначально означающее «камешек»; Поскольку такие камешки использовались для расчетов, значение этого слова изменилось и сегодня обычно означает метод расчета. Тем временем, исчисление, первоначально назывался исчисление бесконечно малых или "исчисление бесконечно малые ", это исследование непрерывный изменять.

Дискретное исчисление имеет две точки входа: дифференциальное исчисление и интегральное исчисление. Дифференциальное исчисление касается возрастающих темпов изменения и наклонов кусочно-линейных кривых. Интегральное исчисление касается накопления величин и площадей под кусочно-постоянными кривыми. Эти две точки зрения связаны друг с другом основной теоремой дискретного исчисления.

Изучение концепций изменения начинается с их дискретной формы. Развитие зависит от параметра, приращение ${ displaystyle Delta x}$ независимой переменной. Если мы так выберем, мы можем делать приращение все меньше и меньше и найти непрерывные аналоги этих концепций как пределы. Неформально предел дискретного исчисления как ${ displaystyle Delta x to 0}$ исчисление бесконечно малых. Несмотря на то, что оно служит дискретной основой исчисления, основная ценность дискретного исчисления заключается в приложениях.

Две исходные конструкции

Дискретное дифференциальное исчисление это изучение определения, свойств и приложений коэффициент разницы функции. Процесс нахождения коэффициента разности называется дифференциация. Учитывая функцию, определенную в нескольких точках реальной линии, коэффициент разности в этой точке является способом кодирования мелкомасштабного (то есть от точки к следующей) поведения функции. Найдя коэффициент разности функции в каждой паре последовательных точек в ее области определения, можно создать новую функцию, называемую функция разностного частного или просто коэффициент разницы исходной функции. Формально, коэффициент разности равен линейный оператор который принимает функцию на входе и создает вторую функцию на выходе. Это более абстрактно, чем многие процессы, изучаемые в элементарной алгебре, где функции обычно вводят число и выводят другое число. Например, если функции удвоения дан вход три, то она выдает шесть, а если функция возведения в квадрат - вход три, то она выдает девять. Однако производная может принимать функцию возведения в квадрат в качестве входных данных. Это означает, что производная принимает всю информацию функции возведения в квадрат, например, что два отправляются на четыре, три отправляются на девять, четыре отправляются на шестнадцать и так далее, и использует эту информацию для создания другой функции. Функция, полученная путем дифференцирования функции возведения в квадрат, оказывается чем-то близким к функции удвоения.

Предположим, что функции определены в точках, разделенных приращением ${ displaystyle Delta x = h> 0}$ :

{ displaystyle a, a + h, a + 2h, ldots, a + nh, ldots}

«Функция удвоения» может быть обозначена как ${ Displaystyle г (х) = 2х}$ и "функция возведения в квадрат" ${ Displaystyle е (х) = х ^ {2}}$ . «Коэффициент разности» - это скорость изменения функции на одном из интервалов. ${ Displaystyle [х, х + ч]}$ определяется формулой:

{ displaystyle { frac {f (x + h) -f (x)} {h}}.}

Требуется функция ${ displaystyle f}$ в качестве входных данных это вся информация - например, что два отправляются на четыре, три отправляются на девять, четыре отправляются на шестнадцать и т. д. - и использует эту информацию для вывода другой функции, функции ${ displaystyle g (x) = 2x + h}$ , как получится. Для удобства новую функцию можно определить в средних точках вышеуказанных интервалов:

{ displaystyle a + h / 2, a + h + h / 2, a + 2h + h / 2, ..., a + nh + h / 2, ...}

Поскольку скорость изменения такова, что для всего интервала ${ Displaystyle [х, х + ч]}$ , любая точка в нем может использоваться в качестве такой ссылки или, что еще лучше, весь интервал, который делает разность коэффициентом a ${ displaystyle 1}$ -коцепь.

Наиболее распространенное обозначение коэффициента разности:

{ displaystyle { frac { Delta f} { Delta x}} (x + h / 2) = { frac {f (x + h) -f (x)} {h}}.}

Если входные данные функции представляют время, то коэффициент разницы представляет изменение относительно времени. Например, если ${ displaystyle f}$ - функция, которая принимает время в качестве входных данных и выдает положение мяча в этот момент в качестве выходных данных, тогда коэффициент разности ${ displaystyle f}$ как позиция меняется во времени, то есть это скорость мяча.

Если функция линейный (то есть, если точки график функции лежат на прямой), то функцию можно записать как ${ displaystyle y = mx + b}$ , куда ${ displaystyle x}$ - независимая переменная, ${ displaystyle y}$ зависимая переменная, ${ displaystyle b}$ это ${ displaystyle y}$ -перехват, и:

{ displaystyle m = { frac { text {rise}} { text {run}}} = { frac {{ text {change in}} y} {{ text {change in}} x}} = { frac { Delta y} { Delta x}}.}

Это дает точное значение для склон прямой.

Склон:

{ displaystyle m = left ({ frac { Delta y} { Delta x}} right) = tan ( theta)}

Если же функция не является линейной, то изменение ${ displaystyle y}$ делится на изменение ${ displaystyle x}$ меняется. Коэффициент разницы дает точное значение понятию изменения выпуска по отношению к изменению на входе. Чтобы быть конкретным, позвольте ${ displaystyle f}$ быть функцией и зафиксировать точку ${ displaystyle x}$ в области ${ displaystyle f}$ . ${ Displaystyle (х, е (х))}$ - точка на графике функции. Если ${ displaystyle h}$ это приращение ${ displaystyle x}$ , тогда ${ displaystyle x + h}$ следующее значение ${ displaystyle x}$ . Следовательно, ${ Displaystyle (х + ч, е (х + ч))}$ это приращение ${ Displaystyle (х, е (х))}$ . Наклон линии между этими двумя точками равен

{ displaystyle m = { frac {f (x + h) -f (x)} {(x + h) -a}} = { frac {f (x + h) -f (x)} {h }}.}

Так ${ displaystyle m}$ это наклон линии между ${ Displaystyle (х, е (х))}$ и ${ Displaystyle (х + ч, е (х + ч))}$ .

Вот частный пример, разностное отношение функции возведения в квадрат. Позволять ${ Displaystyle е (х) = х ^ {2}}$ - функция возведения в квадрат. Потом:

{ displaystyle { begin {align} { frac { Delta f} { Delta x}} (x) & = {(x + h) ^ {2} -x ^ {2} over {h}} & = {x ^ {2} + 2hx + h ^ {2} -x ^ {2} over {h}} & = {2hx + h ^ {2} over {h}} & = 2x + h. End {выровнено}}}

Фактор разности разностного фактора называется второй фактор разницы и он определен в

{ displaystyle a + h, a + 2h, a + 3h, ldots, a + nh, ldots}

И так далее.

Дискретное интегральное исчисление это изучение определений, свойств и приложений Суммы Римана. Процесс нахождения суммы называется интеграция. Говоря техническим языком, интегральное исчисление изучает определенные линейный оператор.

В Сумма Римана вводит функцию и выводит функцию, которая дает алгебраическую сумму площадей между частью графика ввода и ось абсцисс.

Примером мотивации являются расстояния, пройденные за определенное время.

{ displaystyle { text {distance}} = { text {speed}} cdot { text {time}}}

Если скорость постоянна, требуется только умножение, но если скорость изменяется, мы оцениваем пройденное расстояние, разбивая время на множество коротких интервалов времени, а затем умножая время, прошедшее в каждом интервале, на одну из скоростей в этом интервале. , а затем взяв сумму (a Сумма Римана ) расстояния, пройденного за каждый интервал.

Постоянная скорость

Сумма Римана измеряет общую площадь полосок, определяемую как

{ displaystyle f}

, между двумя точками (здесь

{ displaystyle a}

и

{ displaystyle b}

).

Когда скорость постоянна, общее расстояние, пройденное за данный интервал времени, можно вычислить, умножив скорость на время. Например, если вы едете со скоростью 50 миль в час в течение 3 часов, то общее расстояние составит 150 миль. На диаграмме слева, когда изображены постоянная скорость и время, эти два значения образуют прямоугольник с высотой, равной скорости, и шириной, равной истекшему времени. Следовательно, произведение скорости и времени также вычисляет прямоугольную область под кривой (постоянной) скорости. Эта связь между площадью под кривой и пройденным расстоянием может быть расширена до любой область неправильной формы, демонстрирующая постепенно изменяющуюся скорость в течение заданного периода времени. Если столбцы на диаграмме справа представляют скорость, изменяющуюся от одного интервала к следующему, пройденное расстояние (между временами, представленными ${ displaystyle a}$ и ${ displaystyle b}$ ) - площадь заштрихованной области ${ displaystyle s}$ .

Итак, интервал между ${ displaystyle a}$ и ${ displaystyle b}$ делится на ряд равных сегментов, длина каждого сегмента представлена символом ${ displaystyle Delta x}$ . Для каждого небольшого отрезка у нас есть одно значение функции ${ displaystyle f (x)}$ . Назовите это значение ${ displaystyle v}$ . Тогда площадь прямоугольника с основанием ${ displaystyle Delta x}$ и высота ${ displaystyle v}$ дает расстояние (время ${ displaystyle Delta x}$ умноженный на скорость ${ displaystyle v}$ ) ездил в том сегменте. С каждым сегментом связано значение функции над ним, ${ Displaystyle е (х) = v}$ . Сумма всех таких прямоугольников дает площадь между осью и кусочно-постоянной кривой, которая представляет собой общее пройденное расстояние.

Предположим, что функция определена в серединах интервалов равной длины ${ displaystyle Delta x = h> 0}$ :

{ displaystyle a + h / 2, a + h + h / 2, a + 2h + h / 2, ldots, a + nh-h / 2, ldots}

Тогда сумма Римана из ${ displaystyle a}$ к ${ displaystyle b = a + nh}$ в сигма-обозначение является:

{ displaystyle sum _ {i = 1} ^ {n} f (a + ih) , Delta x.}

Поскольку это вычисление выполняется для каждого ${ displaystyle n}$ , новая функция определяется в точках:

{ displaystyle a, a + h, a + 2h, ldots, a + nh, ldots}

В основная теорема исчисления утверждает, что дифференцирование и интегрирование - обратные операции. Точнее, он связывает разностные коэффициенты с суммами Римана. Это также может быть истолковано как точное утверждение того факта, что дифференцирование является обратным интегрированию.

Основная теорема исчисления: если функция ${ displaystyle f}$ определяется на разбиении интервала ${ Displaystyle [а, б]}$ , ${ displaystyle b = a + nh}$ , и если ${ displaystyle F}$ функция, разностный коэффициент которой равен ${ displaystyle f}$ , то имеем:

{ displaystyle sum _ {i = 0} ^ {n-1} f (a + ih + h / 2) , Delta x = F (b) -F (a).}

Кроме того, для каждого ${ textstyle m = 0,1,2, ldots, n-1}$ , у нас есть:

{ displaystyle { frac { Delta} { Delta x}} sum _ {i = 0} ^ {m} f (a + ih + h / 2) , Delta x = f (a + mh + ч / 2).}

Это тоже прототип решения разностное уравнение. Уравнения разности связывают неизвестную функцию с ее разностным или разностным коэффициентом и повсеместно используются в науках.

История

Ранняя история дискретного исчисления - это история исчисления. Такие базовые идеи, как коэффициенты разницы и Суммы Римана неявно или явно фигурируют в определениях и доказательствах. Однако после того, как лимит исчерпан, их больше никогда не увидят. Тем не менее Закон напряжения Кирхгофа (1847) можно выразить через одномерную дискретную внешнюю производную.

В течение ХХ века дискретное исчисление остается взаимосвязанным с исчислением бесконечно малых, особенно с дифференциальными формами, но также начинает опираться на алгебраическая топология как развиваются оба. Основные взносы поступают от следующих лиц:^[1]

Анри Пуанкаре: триангуляции (барицентрическое подразделение, двойная триангуляция ), Лемма Пуанкаре, первое доказательство общей Теорема Стокса, и многое другое
Л. Э. Дж. Брауэр: симплициальная аппроксимационная теорема
Эли Картан, Жорж де Рам: понятие дифференциальной формы, внешняя производная как координатно-независимый линейный оператор, точность / замкнутость форм
Эмми Нётер, Хайнц Хопф, Леопольд Виеторис, Вальтер Майер: модули из цепи, то граничный оператор, цепные комплексы
Дж. В. Александер, Соломон Лефшец, Лев Понтрягин, Андрей Колмогоров, Норман Стинрод, Эдуард Чех: рано коцепь понятия
Герман Вейль: законы Кирхгофа, сформулированные в терминах граничных и кограничных операторов
В. В. Д. Ходж: the Звездный оператор Ходжа, то Разложение Ходжа
Сэмюэл Эйленберг, Saunders Mac Lane, Норман Стинрод, J.H.C. Уайтхед: тщательная разработка теория гомологии и когомологий включая цепные и коцепные комплексы, чашка продукта
Хасслер Уитни: коцепи как интегрируемые

Недавнее развитие дискретного исчисления, начиная с Уитни, было обусловлено потребностями прикладное моделирование. ^[2] ^[3]^[4]

Приложения

Дискретное исчисление используется для моделирования прямо или косвенно как дискретизация бесконечно малых исчисление во всех областях физических наук, актуарная наука, Информатика, статистика, инженерное дело, экономика, бизнес, лекарство, демография, и в других областях, где может быть проблема математически смоделированный. Это позволяет перейти от (непостоянных) темпов изменения к полному изменению или наоборот, и много раз, изучая проблему, мы знаем одну и пытаемся найти другую.

Физика особенно использует исчисление; все дискретные концепции в классическая механика и электромагнетизм связаны посредством дискретного исчисления. В масса объекта известных плотность который изменяется постепенно, момент инерции таких объектов, а также полную энергию объекта в дискретном консервативном поле можно найти с помощью дискретного исчисления. Пример использования дискретного исчисления в механике: Второй закон движения Ньютона: исторически заявлено, что в нем явно используется термин «изменение движения», который подразумевает коэффициент разницы, говоря Изменение количества движения тела равно результирующей силе, действующей на тело, и происходит в том же направлении. Сегодня обычно выражается как Сила = Масса × Ускорение, он вызывает дискретное исчисление, когда изменение является инкрементным, потому что ускорение - это коэффициент разности скорости по времени или второй коэффициент разности пространственного положения. Зная, как объект ускоряется, мы используем суммы Римана для определения его пути.

Теория Максвелла электромагнетизм и Эйнштейн теория общая теория относительности были выражены на языке дискретного исчисления.

Химия использует расчет для определения скорости реакции и радиоактивного распада (экспоненциальный спад ).

В биологии популяционная динамика начинается с воспроизводства и смертности для моделирования популяционных изменений (моделирование населения ).

В машиностроении, разностные уравнения используются для построения курса космического корабля в условиях невесомости, для моделирования теплопередача, распространение, и распространение волн.

Дискретный Теорема Грина применяется в инструменте, известном как планиметр, который используется для вычисления площади плоской поверхности на чертеже. Например, его можно использовать для расчета площади, занимаемой клумбой неправильной формы или плавательным бассейном при проектировании планировки участка земли. Его можно использовать для эффективного вычисления суммы прямоугольных областей на изображениях, чтобы быстро извлекать особенности и обнаруживать объект; другой алгоритм, который можно использовать, - это таблица суммированных площадей.

В области медицины исчисление можно использовать для определения оптимального угла разветвления кровеносного сосуда, чтобы максимизировать поток. Из законов распада для выведения определенного лекарства из организма он используется для получения законов дозирования. В ядерной медицине он используется для построения моделей переноса излучения при целенаправленной терапии опухолей.

В экономике расчет позволяет определить максимальную прибыль путем расчета как предельная стоимость и предельный доход, а также моделирование рынков. ^[5]

Дискретное исчисление можно использовать в сочетании с другими математическими дисциплинами. Например, его можно использовать в теория вероятности для определения вероятности дискретной случайной величины из предполагаемой функции плотности.

Исчисление разностей и сумм

Предположим, что функция (a ${ displaystyle 0}$ -cochain) ${ displaystyle f}$ определяется в точках, разделенных приращением ${ displaystyle Delta x = h> 0}$ :

{ displaystyle a, a + h, a + 2h, ldots, a + nh, ldots}

В разница (или внешняя производная, или кограничный оператор) функции задается следующим образом:

{ displaystyle { big (} Delta f { big)} { big (} [x, x + h] { big)} = f (x + h) -f (x).}

Он определяется в каждом из вышеуказанных интервалов; это ${ displaystyle 1}$ -cochain.

Предположим, что ${ displaystyle 1}$ -cochain ${ displaystyle g}$ определяется в каждом из указанных выше интервалов. Тогда его сумма является функцией (a ${ displaystyle 0}$ -cochain) определяется в каждой из точек:

{ displaystyle left ( sum g right) (a + nh) = sum _ {i = 1} ^ {n} g { big (} [a + (i-1) h, a + ih] { большой )}.}

Вот их свойства:

Постоянное правило: Если ${ displaystyle c}$ это постоянный, тогда

{ displaystyle Delta c = 0}

Линейность: если ${ displaystyle a}$ и ${ displaystyle b}$ находятся константы,

{ Displaystyle Delta (af + bg) = a , Delta f + b , Delta g, quad sum (af + bg) = a , sum f + b , sum g}

Правило продукта:

{ Displaystyle Delta (fg) = е , Delta g + g , Delta f + Delta f , Delta g}

Основная теорема исчисления я:

{ Displaystyle влево ( сумма Дельта е вправо) (a + nh) = f (a + nh) -f (a)}

Основная теорема исчисления II:

{ Displaystyle Дельта влево ( сумма г вправо) = г}

Определения применяются к графики следующим образом. Если функция (a ${ displaystyle 0}$ -cochain) ${ displaystyle f}$ определяется в узлах графа:

{ displaystyle a, b, c, ldots}

тогда это внешняя производная (или дифференциал) - это разность, т.е. следующая функция, определенная на ребрах графа ( ${ displaystyle 1}$ -cochain):

{ displaystyle left (df right) { big (} [a, b] { big)} = f (b) -f (a).}

Если ${ displaystyle g}$ это ${ displaystyle 1}$ -cochain, тогда его интеграл над последовательностью ребер ${ displaystyle sigma}$ графа есть сумма его значений по всем ребрам ${ displaystyle sigma}$ («интеграл по путям»):

{ displaystyle int _ { sigma} g = sum _ { sigma} g { big (} [a, b] { big)}.}.

Это свойства:

Постоянное правило: Если ${ displaystyle c}$ это постоянный, тогда

{ displaystyle dc = 0}

Линейность: если ${ displaystyle a}$ и ${ displaystyle b}$ находятся константы,

{ Displaystyle d (af + bg) = a , df + b , dg, quad int _ { sigma} (af + bg) = a , int _ { sigma} f + b , int _ { sigma} g}

Правило продукта:

{ Displaystyle d (fg) = f , dg + g , df + df , dg}

Основная теорема исчисления I: если ${ displaystyle 1}$ -цепь ${ displaystyle sigma}$ состоит из краев ${ displaystyle [a_ {0}, a_ {1}], [a_ {1}, a_ {2}], ..., [a_ {n-1}, a_ {n}]}$ , то для любого ${ displaystyle 0}$ -cochain ${ displaystyle f}$

{ displaystyle int _ { sigma} df = f (a_ {n}) - f (a_ {0})}

Основная теорема исчисления II: если график дерево, ${ displaystyle g}$ это ${ displaystyle 1}$ -cochain и функция ( ${ displaystyle 0}$ -cochain) определяется на узлах графа как

{ Displaystyle е (х) = int _ { sigma} г}

где ${ displaystyle 1}$ -цепь ${ displaystyle sigma}$ состоит из ${ displaystyle [a_ {0}, a_ {1}], [a_ {1}, a_ {2}], ..., [a_ {n-1}, x]}$ для некоторых фиксированных ${ displaystyle a_ {0}}$ , тогда

{ displaystyle df = g}

См. Ссылки.^[6]^[7]^[8]^[9]^[3]^[10]

Цепочки симплексов и кубов

Симплициальный комплекс.

А симплициальный комплекс ${ displaystyle S}$ это набор симплексы который удовлетворяет следующим условиям:

1. Каждый лицо симплекса от

{ displaystyle S}

также в

{ displaystyle S}

.

2. Непустой пересечение любых двух симплексов

{ displaystyle sigma _ {1}, sigma _ {2} in S}

это лицо обоих

{ displaystyle sigma _ {1}}

и

{ displaystyle sigma _ {2}}

.

Берется граница границы 2-симплекса (слева) и граница 1-цепи (справа). Оба равны 0, являясь суммой, в которой как положительное, так и отрицательное значение 0-симплекса встречаются один раз. Граница границы всегда равна 0. Нетривиальный цикл - это то, что замыкается, как граница симплекса, в том смысле, что его граница равна 0, но на самом деле это не граница симплекса или цепи.

По определению ориентация из k-симплекс задается порядком вершин, записываемым как ${ displaystyle (v_ {0}, ..., v_ {k})}$ , с правилом, что два порядка определяют одну и ту же ориентацию тогда и только тогда, когда они отличаются даже перестановка. Таким образом, каждый симплекс имеет ровно две ориентации, и изменение порядка двух вершин меняет ориентацию на противоположную. Например, выбор ориентации 1-симплекса означает выбор одного из двух возможных направлений, а выбор ориентации 2-симплекса означает выбор того, что должно означать «против часовой стрелки».

Позволять ${ displaystyle S}$ - симплициальный комплекс. А симплициальный k-цепь конечный формальная сумма

{ Displaystyle сумма _ {я = 1} ^ {N} c_ {я} sigma _ {я}, ,}

где каждый c_я целое число и σ_я ориентированный k-симплекс. В этом определении мы заявляем, что каждый ориентированный симплекс равен негативу симплекса с противоположной ориентацией. Например,

{ displaystyle (v_ {0}, v_ {1}) = - (v_ {1}, v_ {0}).}

В векторное пространство из k-цепи на ${ displaystyle S}$ написано ${ displaystyle C_ {k}}$ . Он имеет основу во взаимно однозначном соответствии с множеством k-симплексы в ${ displaystyle S}$ . Чтобы явно определить базис, нужно выбрать ориентацию каждого симплекса. Один из стандартных способов сделать это - выбрать порядок всех вершин и задать каждому симплексу ориентацию, соответствующую индуцированному порядку его вершин.

Позволять ${ displaystyle sigma = (v_ {0}, ..., v_ {k})}$ быть ориентированным k-симплекс, рассматриваемый как базовый элемент ${ displaystyle C_ {k}}$ . В граничный оператор

{ displaystyle partial _ {k}: C_ {k} rightarrow C_ {k-1}}

это линейный оператор определяется:

{ displaystyle partial _ {k} ( sigma) = sum _ {i = 0} ^ {k} (- 1) ^ {i} (v_ {0}, dots, { widehat {v_ {i) }}}, точки, v_ {k}),}

где ориентированный симплекс

{ displaystyle (v_ {0}, dots, { widehat {v_ {i}}}, dots, v_ {k})}

это ${ displaystyle i}$ я лицо ${ displaystyle sigma}$ , полученный удалением его ${ displaystyle i}$ -я вершина.

В ${ displaystyle C_ {k}}$ , элементы подгруппы

{ Displaystyle Z_ {k} = ker partial _ {k}}

упоминаются как циклы, а подгруппа

{ displaystyle B_ {k} = operatorname {im} partial _ {k + 1}}

как говорят, состоит из границы.

Прямое вычисление показывает, что ${ Displaystyle partial ^ {2} = 0}$ . Говоря геометрическими терминами, это означает, что граница чего-либо не имеет границ. Эквивалентно векторные пространства ${ displaystyle (C_ {k}, partial _ {k})}$ сформировать цепной комплекс. Другое эквивалентное утверждение состоит в том, что ${ displaystyle B_ {k}}$ содержится в ${ displaystyle Z_ {k}}$ .

А кубический комплекс это набор состоит из точки, отрезки линии, квадраты, кубики, и их п-размерные аналоги. Они используются аналогично симплексам для образования комплексов. An элементарный интервал это подмножество ${ Displaystyle I подмножество mathbf {R}}$ формы

{ Displaystyle I = [ ell, ell +1] quad { text {или}} quad I = [ ell, ell]}

для некоторых ${ displaystyle ell in mathbf {Z}}$ . An элементарный куб ${ displaystyle Q}$ является конечным произведением элементарных интервалов, т. е.

{ displaystyle Q = I_ {1} times I_ {2} times cdots times I_ {d} subset mathbf {R} ^ {d}}

куда ${ displaystyle I_ {1}, I_ {2}, ldots, I_ {d}}$ являются элементарными интервалами. Аналогично, элементарный куб - это любой перевод единичного куба. ${ Displaystyle [0,1] ^ {п}}$ встроенный в Евклидово пространство ${ displaystyle mathbf {R} ^ {d}}$ (для некоторых ${ displaystyle n, d in mathbf {N} cup {0 }}$ с ${ Displaystyle п leq d}$ ). Множество ${ Displaystyle X substeq mathbf {R} ^ {d}}$ это кубический сложный если его можно записать как объединение элементарных кубов (или, возможно, гомеоморфный к такому набору), и он содержит все грани всех своих кубов. Граничный оператор и цепной комплекс определяются аналогично симплициальным комплексам.

Более общие клеточные комплексы.

А цепной комплекс ${ displaystyle (C _ {*}, partial _ {*})}$ это последовательность векторные пространства ${ Displaystyle ldots, C_ {0}, C_ {1}, C_ {2}, C_ {3}, C_ {4}, ldots}$ связаны линейные операторы (называется граничные операторы) ${ displaystyle partial _ {n}: C_ {n} to C_ {n-1}}$ , такая что композиция любых двух последовательных отображений является нулевой. Явно граничные операторы удовлетворяют ${ displaystyle partial _ {n} circ partial _ {n + 1} = 0}$ , или с подавленными индексами, ${ displaystyle partial ^ {2} = 0}$ . Комплекс можно записать следующим образом.

{ displaystyle cdots { xleftarrow { partial _ {0}}} C_ {0} { xleftarrow { partial _ {1}}} C_ {1} { xleftarrow { partial _ {2}}} C_ {2} { xleftarrow { partial _ {3}}} C_ {3} { xleftarrow { partial _ {4}}} C_ {4} { xleftarrow { partial _ {5}}} cdots}

А симплициальная карта - это карта между симплициальными комплексами, обладающая тем свойством, что изображения вершин симплекса всегда покрывают симплекс (следовательно, вершины имеют вершины для изображений). Симплициальная карта ${ displaystyle f}$ из симплициального комплекса ${ displaystyle S}$ другому ${ displaystyle T}$ - функция из множества вершин ${ displaystyle S}$ к множеству вершин ${ displaystyle T}$ такое, что изображение каждого симплекса в ${ displaystyle S}$ (рассматриваемый как набор вершин) представляет собой симплекс в ${ displaystyle T}$ . Он генерирует линейную карту, называемую карта цепи, из цепного комплекса ${ displaystyle S}$ к цепному комплексу ${ displaystyle T}$ . В явном виде это указано на ${ displaystyle k}$ -цепи по

{ Displaystyle е ((v_ {0}, ldots, v_ {k})) = (f (v_ {0}), ldots, f (v_ {k}))}

если ${ displaystyle f (v_ {0}), ..., f (v_ {k})}$ все различны, в противном случае он полагается равным ${ displaystyle 0}$ .

А карта цепи ${ displaystyle f}$ между двумя цепными комплексами ${ displaystyle (A _ {*}, d_ {A, *})}$ и ${ displaystyle (B _ {*}, d_ {B, *})}$ это последовательность ${ displaystyle f _ {*}}$ гомоморфизмов ${ displaystyle f_ {n}: A_ {n} rightarrow B_ {n}}$ для каждого ${ displaystyle n}$ который коммутирует с граничными операторами на двух цепных комплексах, поэтому ${ displaystyle d_ {B, n} circ f_ {n} = f_ {n-1} circ d_ {A, n}}$ . Об этом написано в следующем коммутативная диаграмма:

Карта цепи отправляет циклы в циклы и границы в границы.

См. Ссылки.^[11]^[10]^[12]

Дискретные дифференциальные формы: коцепи

Для каждого векторного пространства C_я в цепном комплексе мы рассматриваем его двойное пространство ${ displaystyle C_ {i} ^ {*}: = mathrm {Hom} (C_ {i}, { bf {R}}),}$ и ${ displaystyle d ^ {i} = partial _ {i} ^ {*}}$ это его дуальный линейный оператор

{ displaystyle d ^ {i-1}: C_ {i-1} ^ {*} to C_ {i} ^ {*}.}

Это дает эффект «перевертывания всех стрел» исходного комплекса, оставляя коцепьевой комплекс

{ displaystyle cdots leftarrow C_ {я + 1} ^ {*} { stackrel { partial _ {i} ^ {*}} { leftarrow}} C_ {i} ^ {*} { stackrel { partial _ {i-1} ^ {*}} { leftarrow}} C_ {i-1} ^ {*} leftarrow cdots}

В коцепьевой комплекс ${ displaystyle (C ^ {*}, d ^ {*})}$ это двойной понятие к цепному комплексу. Он состоит из последовательности векторных пространств ${ displaystyle ..., C_ {0}, C_ {1}, C_ {2}, C_ {3}, C_ {4}, ...}$ связаны линейными операторами ${ displaystyle d ^ {n}: от C ^ {n} до C ^ {n + 1}}$ удовлетворение ${ displaystyle d ^ {n + 1} circ d ^ {n} = 0}$ . Комплекс коцепи может быть записан аналогично цепному комплексу.

{ displaystyle cdots { xrightarrow {d ^ {- 1}}} C ^ {0} { xrightarrow {d ^ {0}}} C ^ {1} { xrightarrow {d ^ {1}}} C ^ {2} { xrightarrow {d ^ {2}}} C ^ {3} { xrightarrow {d ^ {3}}} C ^ {4} { xrightarrow {d ^ {4}}} cdots}

Индекс ${ displaystyle n}$ в любом ${ displaystyle C_ {n}}$ или же ${ displaystyle C ^ {n}}$ называется степень (или же измерение). Разница между цепными и коцепными комплексами состоит в том, что в цепных комплексах дифференциалы уменьшают размерность, тогда как в коцепных комплексах они увеличивают размерность.

Элементы отдельных векторных пространств (ко) цепного комплекса называются коцепи. Элементы в ядро из ${ displaystyle d}$ называются коциклы (или же закрыто элементы), а элементы в изображение из ${ displaystyle d}$ называются кограницы (или же точный элементы). Согласно определению дифференциала, все границы являются циклами.

В Лемма Пуанкаре заявляет, что если ${ displaystyle B}$ это открытый мяч в ${ displaystyle { bf {R}} ^ {n}}$ , любые закрытые ${ displaystyle p}$ -форма ${ displaystyle omega}$ определено на ${ displaystyle B}$ точно, для любого целого ${ displaystyle p}$ с ${ displaystyle 1 leq p leq n}$ .

Когда мы называем коцепи дискретные (дифференциальные) формы, мы ссылаемся на ${ displaystyle d}$ как внешняя производная. Мы также используем обозначение исчисления для значений форм:

{ displaystyle omega (s) = int _ {s} omega.}

Теорема Стокса является утверждением о дискретных дифференциальных формах на коллекторы, который обобщает основную теорему дискретного исчисления для разбиения интервала:

{ displaystyle sum _ {я = 0} ^ {n-1} { frac { Delta F} { Delta x}} (a + ih + h / 2) , Delta x = F (b) -F (a).}

Теорема Стокса гласит, что сумма формы ${ displaystyle omega}$ над граница некоторых ориентируемый многообразие ${ displaystyle Omega}$ равна сумме своих внешняя производная ${ displaystyle d omega}$ по всему ${ displaystyle Omega}$ , т.е.

{ displaystyle int _ { Omega} d omega = int _ { partial Omega} omega ,.}

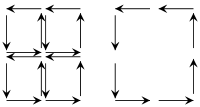
Стоит изучить основной принцип на примере ${ displaystyle d = 2}$ Габаритные размеры. Суть идеи может быть понята из диаграммы слева, которая показывает, что в ориентированном замощении многообразия внутренние пути пересекаются в противоположных направлениях; их вклады в интеграл по путям, таким образом, попарно компенсируют друг друга. Как следствие, остается только вклад от границы.

См. Ссылки.^[11]^[10]

Изделие клина форм

В дискретном исчислении это конструкция, которая создает из форм формы более высокого порядка: соединение двух коцепи степени ${ displaystyle p}$ и ${ displaystyle q}$ образовывать составную коцепь степени ${ displaystyle p + q}$ .

За кубические комплексы, то клин определяется на каждом кубе, рассматриваемом как векторное пространство той же размерности.

За симплициальные комплексы, изделие клина реализовано как чашка продукта: если ${ displaystyle f ^ {p}}$ это ${ displaystyle p}$ -cochain и ${ displaystyle g ^ {q}}$ это ${ displaystyle q}$ -cochain, тогда

{ Displaystyle (е ^ {p} улыбка g ^ {q}) ( sigma) = f ^ {p} ( sigma _ {0,1, ..., p}) cdot g ^ {q} ( sigma _ {p, p + 1, ..., p + q})}

куда ${ displaystyle sigma}$ это ${ Displaystyle (п + д)}$ -симплекс и ${ displaystyle sigma _ {S}, S subset {0,1, ..., p + q }}$ , является симплексом, натянутым на ${ displaystyle S}$ в ${ Displaystyle (п + д)}$ -симплекс, вершины которого индексируются ${ displaystyle {0, ..., p + q }}$ . Так, ${ displaystyle sigma _ {0,1, ..., p}}$ это ${ displaystyle p}$ -го лицевая сторона и ${ displaystyle sigma _ {p, p + 1, ..., p + q}}$ это ${ displaystyle q}$ -го задняя сторона из ${ displaystyle sigma}$ , соответственно.

В кограница чашки продукта коцепей ${ displaystyle f ^ {p}}$ и ${ displaystyle g ^ {q}}$ дан кем-то

{ displaystyle d (f ^ {p} smile g ^ {q}) = d {f ^ {p}} smile g ^ {q} + (- 1) ^ {p} (f ^ {p} улыбнись d {g ^ {q}}).}

Чашечное произведение двух коциклов снова является коциклом, а произведение кограницы с коциклом (в любом порядке) является кограницей.

Операция с продуктом чашки соответствует идентичности

{ displaystyle alpha ^ {p} smile beta ^ {q} = (- 1) ^ {pq} ( beta ^ {q} smile alpha ^ {p}).}

Другими словами, соответствующее умножение градуированный коммутативный.

См. Ссылки.^[11]

Оператор Лапласа

Оператор Лапласа ${ displaystyle Delta f}$ функции ${ displaystyle f}$ в вершине ${ displaystyle p}$ , - (с точностью до множителя) скорость, с которой среднее значение ${ displaystyle f}$ над клеточной окрестностью ${ displaystyle p}$ отклоняется от ${ displaystyle f (p)}$ . Оператор Лапласа представляет собой плотность потока из градиентный поток функции. Например, чистая скорость, с которой химическое вещество, растворенное в жидкости, движется к некоторой точке или от нее, пропорциональна оператору Лапласа химической концентрации в этой точке; выраженное символически, результирующее уравнение является уравнение диффузии. По этим причинам он широко используется в науке для моделирования различных физических явлений.