Дедушка парадокс - Grandfather paradox

Для персонажа в Доктор Кто и Парадокс фракции франшизы, см Дедушка Парадокс (Доктор Кто).
Смотрите также: Парадокс предопределения
Вверху: оригинальная траектория бильярдного шара. В центре: бильярдный шар появляется из будущего и наносит своему прошлому «я» удар, предотвращающий попадание мяча прошлого в машину времени. Внизу: бильярдный шар никогда не попадает в машину времени, что приводит к парадоксу, ставящему под сомнение, как его старшее «я» могло когда-либо выйти из машины времени и изменить ее курс.

В дедушка парадокс это парадокс из путешествие во времени в котором несоответствия возникают из-за изменения прошлого.[1] Название происходит от общего описания парадокса: человек путешествует в прошлое и убивает своего дедушку до зачатия своего отца или матери, что препятствует существованию путешественника во времени.[2] Несмотря на название, парадокс дедушки не рассматривает исключительно противоречие убийства собственного деда, чтобы предотвратить его рождение. Скорее, парадокс касается любого действия, которое изменяет прошлое,[3] поскольку противоречие возникает всякий раз, когда прошлое становится отличным от того, каким оно было.[4]

Ранние примеры

Парадокс дедушки упоминался в письменных рассказах еще в 1929 году. В 1931 году он был описан как «извечный аргумент в пользу предотвращения вашего рождения путем убийства своих бабушек и дедушек» в письме американцам. научная фантастика журнал Удивительные истории.[5] Ранние научно-фантастические рассказы, посвященные парадоксу, - это короткие рассказы Голос предков от Натаниэль Шахнер, опубликовано в 1933 г.,[6] и книга 1944 года Будущие времена три от Рене Барджавель, хотя в ряде других работ 1930-х и 1940-х годов эта тема затрагивалась с разной степенью детализации.[5]

Варианты

Парадокс дедушки заключает в себе любое изменение прошлого,[4] и представлен во многих вариациях. Физик Джон Гаррисон и др. представляют собой вариант парадокса электронной схемы, которая посылает сигнал через машину времени, чтобы отключиться, и принимает сигнал до того, как отправит его.[7][8] Эквивалентный парадокс известен в философия как «парадокс ретро-самоубийства» или «самоубийство», возвращение в прошлое и убийство более молодой версии самого себя (например, ребенка).[9][10] Другой вариант парадокса дедушки - это «парадокс Гитлера» или «парадокс убийства Гитлера»,[11] довольно частый образ в научной фантастике, в котором главный герой возвращается во времени, чтобы убить Адольф Гитлер прежде чем он сможет спровоцировать Вторая Мировая Война и Холокост. Вместо того, чтобы обязательно физически предотвращать путешествия во времени, действие устраняет любые причина для путешествия, наряду с любым знанием того, что причина когда-либо существовала.[12] Кроме того, последствия существования Гитлера настолько монументальны и всеобъемлющи, что для любого, кто родился после войны, вполне вероятно, что на их рождение каким-то образом повлияли ее последствия, и, таким образом, аспект парадокса, связанный с происхождением, будет непосредственно применяться в некоторых странах. путь.[13]

Некоторые выступают за параллельная вселенная подход к дедовскому парадоксу. Когда путешественник во времени убивает своего деда, он фактически убивает версию дедушки из параллельной вселенной, и исходная вселенная путешественника во времени остается неизменной; Утверждалось, что, поскольку путешественник попадает в историю другой вселенной, а не в свою собственную историю, это не «настоящее» путешествие во времени.[14] В других вариантах действия путешественников во времени не влияют на их личный опыт, как показано на Альфред Бестер короткий рассказ Люди, убившие Мухаммеда.[неосновной источник необходим ]

Философский анализ

Даже не зная, возможно ли путешествие во времени в прошлое физически, можно показать, используя модальная логика что изменение прошлого приводит к логическому противоречию. Если верно, что прошлое произошло определенным образом, то ложно и невозможно, чтобы прошлое произошло каким-либо иным образом. Путешественник во времени не сможет изменить прошлое таким, каким оно было. является; они будут действовать только так, как это уже согласуется с тем, что обязательно произошло.[3][15]

Рассмотрение парадокса дедушки привело некоторых к мысли, что путешествия во времени по самой своей природе парадоксальны и поэтому логически невозможны. Например, философ Брэдли Дауден приводил такие аргументы в учебнике Логическое объяснение, утверждая, что возможность создания противоречия полностью исключает путешествие во времени в прошлое. Однако некоторые философы и ученые считают, что путешествие во времени в прошлое не обязательно должно быть логически невозможным при условии, что нет возможности изменить прошлое.[4] как было предложено, например, Принцип непротиворечивости Новикова. Дауден пересмотрел свою точку зрения после того, как убедился в этом в беседе с философом Норман Шварц.[16]

Общая теория относительности

Рассмотрение возможности обратного путешествия во времени в гипотетической вселенной, описываемой Метрика Гёделя вел знаменитый логик Курт Гёдель утверждать, что время само по себе может быть своего рода иллюзией.[17][18] Он предлагает что-то вроде время блока Представление, в котором время - это просто другое измерение, подобное пространству, со всеми событиями, всегда фиксированными внутри этого четырехмерного «блока».[нужна цитата ]

Причинные петли

Основная статья: Причинная петля

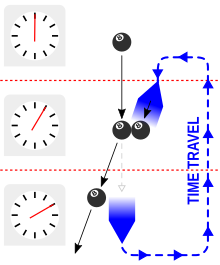
Путешествие во времени назад, которое не создает парадокса дедушки, создает причинную петлю. В Принцип непротиворечивости Новикова выражает одну точку зрения на то, как назад путешествие во времени было бы возможно без порождения парадоксов. Согласно этой гипотезе, физика внутри или вблизи замкнутые времяподобные кривые (машины времени) могут быть согласованы только с универсальными законами физики, и поэтому могут происходить только самосогласованные события. Все, что путешественник во времени делал в прошлом, должно было быть частью истории с самого начала, и путешественник во времени никогда не сможет сделать что-либо, чтобы предотвратить путешествие во времени, поскольку это будет представлять собой несоответствие. Новиков и др. использовал пример, приведенный физиком Джозеф Полчински для дедушкиного парадокса, когда бильярдный шар направляется к машине времени. Старшее «я» мяча выходит из машины времени и ударяет свое более молодое «я», так что его более молодое «я» никогда не входит в машину времени. Новиков и др. показал, как эта система может быть решена самосогласованным способом, который позволяет избежать парадокса дедушки, хотя и создает причинную петлю.[19][20]:510–511 Некоторые физики предполагают, что причинные петли существуют только в квантовом масштабе, аналогично тому, как это происходит в гипотеза защиты хронологии предложено Стивен Хокинг, поэтому истории в более крупных масштабах не зацикливаются.[20]:517 Еще одна гипотеза, гипотеза космической цензуры, предполагает, что каждая замкнутая времениподобная кривая проходит через горизонт событий, что предотвращает наблюдение таких причинных петель.[21]

Сет Ллойд и другие исследователи в Массачусетский технологический институт предложили расширенную версию принципа Новикова, согласно которому вероятность исключает возникновение парадоксов. По мере приближения к запрещенному действию результаты станут более странными, поскольку вселенная должна отдавать предпочтение невероятным событиям, чтобы предотвратить невозможные.[22]

Квантовая физика

Некоторые физики, например Дэниел Гринбергер,[23][24] и Дэвид Дойч, предложили, чтобы квантовая теория позволяет путешествовать во времени, где прошлое должно быть непротиворечивым. Дойч утверждает, что квантовые вычисления с отрицательной задержкой - обратное путешествие во времени - дают только самосогласованные решения, а область, нарушающая хронологию, налагает ограничения, которые не очевидны с помощью классических рассуждений.[25] В 2014 году исследователи опубликовали симуляцию, подтверждающую модель Дойча с фотонами.[26] Дойч использует терминологию «множественных вселенных» в своей статье, пытаясь выразить квантовые явления, но отмечает, что эта терминология неудовлетворительна. Другие считают, что это означает, что «немецкое» путешествие во времени предполагает появление путешественника во времени в другой вселенной, что позволяет избежать парадокса дедушки.[27]

Подход взаимодействующих множественных вселенных является разновидностью Эверетта многомировая интерпретация (MWI) квантовой механики. Он включает в себя путешественников во времени, прибывающих в другую вселенную, чем та, из которой они прибыли; Утверждалось, что, поскольку путешественники прибывают в историю другой вселенной, а не в свою собственную историю, это не «настоящее» путешествие во времени.[14] Стивен Хокинг утверждал, что даже если MWI верен, мы должны ожидать, что каждый путешественник во времени будет испытывать единую самосогласованную историю, чтобы путешественники во времени оставались в своем собственном мире, а не путешествовали в другой.[28] Аллен Эверетт утверждал, что подход Дойча «включает изменение фундаментальных принципов квантовой механики; он определенно выходит за рамки простого принятия MWI», и что даже если подход Дойча верен, это будет означать, что любой макроскопический объект, состоящий из нескольких частиц, будет разделен на части, когда путешествие во времени, с разными частицами, появляющимися в разных мирах.[29]

Однако в статье Толксдорфа и Верха было показано, что условие самосогласованности Дойча CTC может быть выполнено с произвольной точностью в любой квантовой системе, описываемой в соответствии с релятивистскими принципами. квантовая теория поля в пространстве-времени, где CTCs исключены, что вызывает сомнения в том, действительно ли условие Дойча характерно для квантовых процессов, имитирующих CTCs в смысле общая теория относительности.[30]

Смотрите также

использованная литература

  1. ^ Франсиско Лобо (2003). «Время, замкнутые времениподобные кривые и причинность». Nato Sci.ser.ii. 95: 289–296. arXiv:gr-qc / 0206078. Bibcode:2003ntgp.conf..289L.
  2. ^ "Карл Саган обдумывает путешествие во времени". НОВАЯ ЗВЕЗДА. PBS. 10 декабря 1999 г.. Получено 2016-05-21.
  3. ^ а б Норман Шварц (2001), За пределами опыта: метафизические теории и философские ограничения, University of Toronto Press, стр. 226–227.
  4. ^ а б c Николас Дж. Дж. Смит (2013). "Путешествие во времени". Стэнфордская энциклопедия философии. Получено 2 ноября, 2015.
  5. ^ а б Нахин, Пол Дж. (1999). Машины времени: путешествия во времени в физике, метафизике и научной фантастике (2-е изд.). Нью-Йорк: Спрингер. С. 255, 286. ISBN  0387985719.
  6. ^ Джинн, Шерри; Лич, Джиллиан И. (2015). Телевидение, путешествующее во времени: прошлое из настоящего, будущее из прошлого. Лондон: Роуман и Литтлфилд. п. 192. ISBN  978-1442255777.
  7. ^ Гаррисон, J.C .; Mitchell, M.W .; Chiao, R.Y .; Болда, Э. (Август 1998 г.). "Сверхсветовые сигналы: повторение парадоксов причинной петли". Письма о физике A. 245 (1–2): 19–25. arXiv:Quant-ph / 9810031. Bibcode:1998ФЛА..245 ... 19Г. Дои:10.1016 / S0375-9601 (98) 00381-8. S2CID  51796022.
  8. ^ Нахин, Пол Дж. (2016). Истории Машины Времени. Издательство Springer International. С. 335–336. ISBN  9783319488622.
  9. ^ Хорвич, Пол (1987). Асимметрии во времени: проблемы философии науки (2-е изд.). Кембридж, Массачусетс: MIT Press. п. 116. ISBN  0262580888.
  10. ^ Ян Фэй (18 ноября 2015 г.), «Обратная причинность», Стэнфордская энциклопедия философии, получено 25 мая, 2019
  11. ^ Евгения Уильямсон (6 апреля 2013 г.). «Рецензия на книгу: Жизнь после жизни» Кейт Аткинсон ». Бостонский глобус. Получено 9 августа 2013. Погуглите фразу «вернуться в прошлое и», и поисковая система предложит завершить фразу простой директивой: «убить Гитлера». Привлекательность убийства нацистского диктатора настолько велика, что у него есть свой собственный поджанр в спекулятивной фантастике, образ, известный как «парадокс убийства Гитлера», в котором путешественник во времени уезжает достаточно далеко назад, чтобы пресечь лидера - и во Вторую мировую войну - в бутон, обычно с неожиданными последствиями.
  12. ^ Бреннан, Дж. (1997). Путешествие во времени: новая перспектива (1-е изд.). Миннесота: Публикации Ллевеллина. п. 23. ISBN  9781567180855. Вариация парадокса дедушки. . . это парадокс Гитлера. В этом вы путешествуете во времени, чтобы убить Гитлера до того, как он начнет Вторую мировую войну, тем самым спасая миллионы жизней. Но если вы убьете Гитлера, скажем, в 1938 году, тогда Вторая мировая война никогда не начнется, и у вас не будет причин путешествовать во времени, чтобы убить Гитлера!
  13. ^ Инглис-Аркелл, Эстер (2012-08-06). «Неужели у нас не хватает времени, чтобы убить Гитлера с помощью путешествия во времени?». io9. Получено 2013-08-12.
  14. ^ а б Франк Арнцениус; Тим Модлин (23 декабря 2009 г.), «Путешествие во времени и современная физика», Стэнфордская энциклопедия философии, получено 25 мая, 2019
  15. ^ Даммит, Майкл (1996). Море языка (Новое изд.). Оксфорд: Издательство Оксфордского университета. С. 368–369. ISBN  0198236212.
  16. ^ Норман Шварц (1993). "Путешествие во времени - посещение прошлого". SFU.ca. Получено 2016-04-21.
  17. ^ Yourgrau, Palle (4 марта 2009 г.). Мир без времени: забытое наследие Геделя и Эйнштейна. Нью-Йорк: Основные книги. п. 134. ISBN  9780786737000. Получено 18 декабря, 2017.
  18. ^ Холт, Джим (21 февраля 2005 г.). "Бандиты времени". Житель Нью-Йорка. Получено 2017-12-13.
  19. ^ Лосев, Андрей; Новиков, Игорь (15 мая 1992 г.). «Джинн машины времени: нетривиальные самосогласованные решения» (PDF). Класс. Квантовая гравитация. 9 (10): 2309–2321. Bibcode:1992CQGra ... 9.2309L. Дои:10.1088/0264-9381/9/10/014. Архивировано из оригинал (PDF) 17 ноября 2015 г.. Получено 16 ноября 2015.
  20. ^ а б Торн, Кип С. (1995). Черные дыры и искажения времени: возмутительное наследие Эйнштейна. Нью-Йорк: W.W. Нортон. ISBN  0393312763.
  21. ^ Виссер, Мэтт (15 апреля 1997 г.). "Проходные червоточины: Римское кольцо". Физический обзор D. 55 (8): 5212–5214. arXiv:gr-qc / 9702043. Bibcode:1997ПхРвД..55.5212В. Дои:10.1103 / PhysRevD.55.5212. S2CID  2869291.
  22. ^ Сандерс, Лаура (20.07.2010). «Физики приручили путешествия во времени, запретив вам убить своего дедушку». ПРОВОДНОЙ. Получено 2017-01-02. Но это изречение против парадоксальных событий приводит к тому, что возможные маловероятные события происходят чаще. «Если немного изменить начальные условия, парадоксальной ситуации не произойдет. Похоже, это хорошо, но это означает, что если вы очень близки к парадоксальному состоянию, то незначительные различия будут чрезвычайно заметны », - говорит Чарльз Беннетт из исследовательского центра IBM Watson в Йорктаун-Хайтс, Нью-Йорк.
  23. ^ Гринбергер, Дэниел М .; Свозил, Карл (2005). «Квантовая теория смотрит на путешествия во времени». Quo Vadis Quantum Mechanics?. Коллекция Frontiers. п. 63. arXiv:Quant-ph / 0506027. Bibcode:2005qvqm.book ... 63G. Дои:10.1007/3-540-26669-0_4. ISBN  3-540-22188-3. S2CID  119468684.
  24. ^ Кеттлвелл, Джулианна (17 июня 2005 г.). «Новая модель» позволяет путешествовать во времени'". Новости BBC. Получено 26 апреля, 2017.
  25. ^ Дойч, Дэвид (15 ноября 1991 г.). «Квантовая механика около замкнутых времениподобных линий». Физический обзор D. 44 (10): 3197–3217. Bibcode:1991ПхРвД..44.3197Д. Дои:10.1103 / PhysRevD.44.3197. PMID  10013776.
  26. ^ Рингбауэр, Мартин; Брум, Мэтью А .; Майерс, Кейси Р.; White, Andrew G .; Ральф, Тимоти С. (19 июня 2014 г.). «Экспериментальное моделирование замкнутых времениподобных кривых». Nature Communications. 5: 4145. arXiv:1501.05014. Bibcode:2014 НатКо ... 5.4145R. Дои:10.1038 / ncomms5145. PMID  24942489. S2CID  12779043.
  27. ^ Ли Биллингс (2 сентября 2014 г.). "Моделирование путешествия во времени разрешает парадокс дедушки"'". Scientific American. Получено 24 сентября 2014.
  28. ^ Хокинг, Стивен (1999). "Искажения пространства и времени". Получено 25 февраля, 2012.
  29. ^ Эверетт, Аллен (2004). «Парадоксы путешествий во времени, интегралы по траекториям и многомировая интерпретация квантовой механики». Физический обзор D. 69 (124023): 124023. arXiv:gr-qc / 0410035. Bibcode:2004ПхРвД..69л4023Э. Дои:10.1103 / PhysRevD.69.124023. S2CID  18597824.
  30. ^ Толксдорф, Юрген; Верч, Райнер (2018). «Квантовая физика, поля и замкнутые времениподобные кривые: условие D-CTC в квантовой теории поля». Коммуникации по математической физике. 357 (1): 319–351. arXiv:1609.01496. Bibcode:2018CMaPh.357..319T. Дои:10.1007 / s00220-017-2943-5. S2CID  55346710.