Площадь оппозиции - Square of opposition

Площадь оппозиции
в Диаграммы Венна, черные области пустой и красные области непустые.
Блеклые стрелки и блеклые красные области применимы в традиционной логике.
Живопись 15 века

В термин логика (филиал философская логика ), квадрат оппозиции диаграмма, представляющая отношения между четырьмя основными категоричные предложения Происхождение квадрата можно проследить до Аристотель проводя различие между двумя противоположностями: противоречие и противоречие Однако Аристотель не рисовал никакой диаграммы. Это было сделано несколько столетий спустя Апулей и Боэций.

Резюме

В традиционной логике предложение (лат. propositio) является устным утверждением (oratio enunciativa), а не смысл утверждения, как в современной философии языка и логики. А категоричное предложение представляет собой простое предложение, содержащее два термина, подлежащее (S) и предикат (P), в котором предикат либо утверждается, либо отрицается для субъекта.

Каждое категоричное предложение сводится к одному из четырех логические формы, названный А, E, я, и О на основе латыни аffяrmo (Утверждаю), за утвердительные предложения А и я, и пеграммо (Я отрицаю), за отрицательные предложения E и О. Это:

  • Утверждение «А», универсальное утвердительное (universalis affirmativa), чья форма на латыни - «omne S est P», обычно переводится как «каждый S является P».
  • Утверждение 'E', универсальный отрицательный (Universalis negativa), Латинская форма 'nullum S est P', обычно переводимая как 'no S are P'.
  • Утверждение «Я», частное утвердительное (specialis affirmativa), Латинское «quoddam S est P», обычно переводится как «некоторые S суть P».
  • Предложение 'O', особенно отрицательное (specialis negativa), Латинское «quoddam S nōn est P», обычно переводится как «некоторые S не являются P».

В табличной форме:

Четыре аристотелевских утверждения
ИмяСимволлатинскийАнглийский*МнемоническийСовременная форма[1]
Универсальный утвердительныйАOmne S est P.Каждый S - это P. (S всегда P.)аffirmo (Подтверждаю)
Универсальный негативENullum S est P.Нет S - это P. (S никогда не будет P.)пеидти (Я отрицаю)
Особо утвердительныйяQuoddam S est P.Некоторые S - это P. (S иногда P.)affяrmo (Подтверждаю)
Особо отрицательныйОQuoddam S nōn est P.Некоторые S не являются P. (S не всегда P.)негро (Я отрицаю)

*Утверждение «А» можно сформулировать как «Все S есть P.» Однако предложение «E», когда оно формулируется соответственно как «Все S не является P.» неоднозначно[2] потому что это может быть предложение E или O, что требует наличия контекста для определения формы; стандартная форма «Нет S есть P» недвусмысленна, поэтому она предпочтительна. Предложение «O» также принимает форму «Иногда S не является P.» и «Некий S не является P.» (буквально латинское Quoddam S nōn est P.)

Аристотель утверждает (в шестой и седьмой главах Peri hermēneias (Περὶ Ἑρμηνείας, латиница De Interpretatione, Англ. «On Interpretation»)), что между этими четырьмя видами предложений существуют определенные логические отношения. Он говорит, что каждому утверждению соответствует в точности одно отрицание и что каждое утверждение и его отрицание «противоположны», так что всегда одно из них должно быть истинным, а другое ложным. Пару утвердительных и отрицательных утверждений он называет «противоречием» (на средневековой латыни: Contradictio). Примеры противоречий: «каждый человек белый» и «не каждый человек белый» (также читается как «некоторые люди не белые»), «ни один человек не белый» и «какой-то человек белый».

«Противоречие» (средневековый: Contrariae) утверждения, таковы, что оба не могут быть правдой одновременно. Примерами этого являются универсальное утвердительное «каждый человек белый» и универсальное отрицательное «ни один человек не белый». Это не может быть правдой одновременно. Однако это не противоречие, потому что оба они могут быть ложными. Например, неверно, что каждый мужчина белый, поскольку некоторые мужчины не белые. Однако неверно также, что нет белых людей, поскольку есть некоторые белые люди.

Поскольку каждое утверждение имеет противоречивую противоположность и поскольку противоречие истинно, когда его противоположность ложна, отсюда следует, что противоположности противоположностей (которые средние века называли подконтрольными, subcontrariae) оба могут быть истинными, но не могут оба быть ложными. Поскольку подконтрольные утверждения являются отрицанием универсальных утверждений, средневековые логики называли их «частными» утверждениями.

Другая логическая оппозиция, подразумеваемая этим, хотя и не упомянутая прямо Аристотелем, - это `` чередование '' (альтернатива), состоящий из «субальтернации» и «суперальтернации». Чередование - это отношение между конкретным утверждением и универсальным утверждением того же качества, при котором одно подразумевается другим. Частное является подчиненным по отношению к универсальному, которое является суперальтерном частного. Например, если «каждый человек белый» верно, то противоположное «ни один человек не белый» - ложно. Следовательно, противоречивое утверждение «какой-то мужчина белый» верно. Точно так же универсальное «ни один человек не белый» подразумевает конкретное «не каждый человек белый».[3][4]

В итоге:

  • Универсальные утверждения противоречат друг другу: «каждый человек праведен» и «никто не праведен» не могут быть истинными вместе, хотя одно может быть истинным, а другое ложным, а также оба могут быть ложными (если хотя бы один человек праведен, и хоть один мужчина не просто так).
  • Конкретные утверждения являются субподрядчиками. «Кто-то справедливый» и «какой-то мужчина не просто» не могут быть ложными вместе.
  • Конкретное утверждение одного качества является второстепенным универсального утверждения того же качества, которое является суперальтерном конкретного утверждения, потому что в аристотелевской семантике «каждый A есть B» подразумевает, что «некоторое A является B» и «никакое A не является B». подразумевает, что «некоторый A не является B». Обратите внимание, что современные формальные интерпретации английских предложений интерпретируют «каждый A is B» как «для любого x, x is A подразумевает, что x is B», что делает нет подразумевают, что «некоторый x есть A». Однако это вопрос семантической интерпретации и не означает, как иногда утверждают, что аристотелевская логика «ошибочна».
  • Универсальное утвердительное и частное отрицание противоречат друг другу. Если какой-то A не является B, не каждый A является B. И наоборот, хотя это не так в современной семантике, считалось, что если каждый A не является B, то какой-то A не является B. Эта интерпретация вызвала трудности (см. Ниже ). В то время как греческий язык Аристотеля представляет собой конкретный негатив не как «некоторые А не Б», а как «не все А есть Б», кто-то в своем комментарии к Peri hermaneias, переводит частный негатив как «quoddam A nōn est B», буквально «некий A не является B», и во всех средневековых трудах по логике принято представлять конкретное суждение таким образом.

Эти отношения стали основой диаграммы, созданной Боэцием и использовавшейся средневековыми логиками для классификации логических отношений. Предложения помещены в четыре угла квадрата, а отношения представлены в виде линий, проведенных между ними, отсюда и название «квадрат оппозиции».

Проблема экзистенциальный импорт

Подпротиворечия, которые средневековые логики представляли в форме quoddam A est B (некоторая конкретная A есть B) и quoddam A non est B (некоторая конкретная A не является B), не могут быть ложными, поскольку их универсальные противоречивые утверждения (каждый A - это B / нет, A - это B) оба не могут быть верными. Это приводит к затруднению, которое впервые было обнаружено Питер Абеляр. «Some A is B», кажется, подразумевает «что-то есть A». Например, «какой-то мужчина белый», кажется, подразумевает, что по крайней мере один человек является мужчиной, а именно человек, который должен быть белым, если «какой-то мужчина белый» верно. Но «какой-то мужчина не белый» также подразумевает, что что-то есть мужчина, а именно человек, который не белый, если утверждение «какой-то человек не белый» верно. Но аристотелевская логика требует, чтобы одно из этих утверждений обязательно было истинным. Оба не могут быть ложными. Следовательно (поскольку оба подразумевают, что что-то является мужчиной), следует, что обязательно что-то есть мужчина, т.е. мужчины существуют. Но (как указывает Абеляр в «Диалектике») неужели люди не могут существовать?[5]

Поскольку абсолютно никакого человека не существует, ни утверждение «каждый человек есть человек» не является истинным, ни «некоторый человек не является человеком».[6]

Абеляр также указывает, что подконтрольные слова, содержащие субъектные термины, ничего не обозначающие, такие как «человек, который есть камень», являются ложными.

Если «каждый каменный человек - камень» верно, то и его обращение per accidens верно («некоторые камни - каменные люди»). Но ни один камень не является каменным человеком, потому что ни этот человек, ни тот человек и т. Д. Не являются камнем. Но также и то, что «некий каменный человек - не камень» ложно по необходимости, поскольку невозможно предположить, что это правда.[7]

Теренс Парсонс утверждает, что древние философы не сталкивались с проблемой экзистенциального значения, поскольку только формы A и I имели экзистенциальное значение.

Утверждения имеют экзистенциальное значение, а отрицательные - нет. Таким образом, древние не видели несогласованности квадрата, сформулированного Аристотель потому что не было непоследовательности.[8]

Он продолжает цитировать средневекового философа Вильгельм Мербеке

В утвердительных предложениях термин всегда используется для предположения чего-либо. Таким образом, если оно ни о чем не предполагает, это утверждение ложно. Однако в отрицательных суждениях утверждается либо то, что термин не предполагает чего-либо, либо что он предполагает что-то, предикат чего действительно отрицается. Таким образом, отрицательное суждение имеет две причины истинности.[9]

И указывает на Боэций 'перевод работы Аристотеля как порождение ошибочного представления о том, что форма O имеет экзистенциальное значение.

Но когда Боэций комментирует этот текст, он иллюстрирует доктрину Аристотеля известной теперь диаграммой и использует формулировку «Некоторые люди не справедливы». Так что это должно было показаться ему естественным эквивалентом на латыни. Нам это кажется странным по-английски, но его это не беспокоило.[10]

Современные площади оппозиции

Квадрат оппозиции Фреге
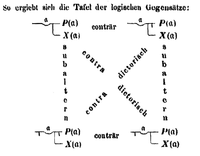
В conträr ниже - ошибка:
Следует читать субподрядчик

В 19 веке, Джордж Буль выступал за требование экзистенциального импорта обоих терминов в конкретных утверждениях (I и O), но допускал, чтобы все термины универсальных утверждений (A и E) не имели экзистенциального значения. Это решение принято Диаграммы Венна особенно прост в использовании для логики терминов. Квадрат оппозиции при этом булевом наборе допущений часто называют современным квадратом оппозиции. В современном квадрате оппозиции утверждения A и O противоречат друг другу, как и E и I, но все другие формы оппозиции перестают существовать; нет никаких противоречий, субподрядчиков или субальтернов. Таким образом, с современной точки зрения, часто имеет смысл говорить о «противоположности» утверждения, а не настаивать, как это делали более старые логики, на том, что у утверждения есть несколько различных противоположностей, которые находятся в разных видах противоположностей с утверждением.

Готлоб Фреге с Begriffsschrift также представляет собой квадрат противоположностей, организованный почти идентично классическому квадрату, демонстрирующий противоречия, субальтернаты и противоречия между четырьмя формулами, построенными на основе универсального количественного определения, отрицания и импликации.

Альгирдас Жюльен Греймас ' семиотический квадрат был получен из работы Аристотеля.

Традиционный квадрат оппозиции теперь часто сравнивают с квадратами, основанными на внутреннем и внешнем отрицании.[11]

Логические шестиугольники и другие би-симплексы

Основная статья: Логический шестиугольник

Квадрат оппозиции был расширен до логического шестиугольника, который включает отношения шести утверждений. Он был открыт независимо обоими Огюстен Сесмат и Роберт Бланше.[12] Было доказано, что и квадрат, и шестиугольник, за которым следует "логический куб ", принадлежат к регулярной серии n-мерных объектов, называемых" логическими би-симплексами размерности n ". Этот шаблон также выходит за рамки этого.[13]

Квадрат оппозиции (или логический квадрат) и модальная логика

Логический квадрат, также называемый квадратом оппозиции или квадратом Апулей берет свое начало в четырех отмеченных предложениях, которые используются в силлогистическом рассуждении: Каждый человек плохой, универсальное утвердительное и его отрицание Не каждый человек плох (или Некоторые люди не плохи), конкретное отрицание, с одной стороны, Некоторые люди плохие, частное утвердительное и его отрицание Ни один человек плохой, универсальный отрицательный с другой. Роберт Бланше опубликовал вместе с Врином его Structures intellectuelles в 1966 году, и с тех пор многие ученые считают, что логический квадрат или квадрат оппозиции, представляющий четыре значения, следует заменить на логический шестиугольник который, представляя шесть значений, является более мощной фигурой, потому что способен объяснить больше вещей о логике и естественном языке.

Смотрите также

Рекомендации

  1. ^ За Традиционная площадь оппозиции: 1.1 Современная версия площади в Стэнфордская энциклопедия философии
  2. ^ Келли, Дэвид (2014). Искусство рассуждать: введение в логику и критическое мышление (4-е изд.). Нью-Йорк, штат Нью-Йорк: W.W. Norton & Company, Inc. стр. 150. ISBN  978-0-393-93078-8.
  3. ^ Парирование и хакер, Аристотелевская логика (SUNY Press, 1990), стр. 158.
  4. ^ Коэн и Нагель, Введение в логику Второе издание (Hackett Publishing, 1993), стр. 55.
  5. ^ В его Диалектика, и в своем комментарии к Перигермании
  6. ^ Re enim hominis prorsus non existente neque ea vera est quae ait: omnis homo est homo, nec ea quae proponit: quidam homo non est homo
  7. ^ Si enim vera est: Omnis homo qui lapis est, est lapis, et eius converta per accidens vera est: Quidam lapis est homo qui est lapis. Sed nullus lapis est homo qui est lapis, quia neque hic neque ille и т. Д. Sed et illam: Quidam homo qui est lapis, non est lapis, falsam esse necesse est, cum невозможно ponat
  8. ^ в Традиционная площадь оппозиции в Стэнфордская энциклопедия философии
  9. ^ (SL I.72) Loux 1974, 206
  10. ^ Традиционная площадь оппозиции
  11. ^ Вестерсталь, «Классические и современные квадраты оппозиции и не только», в Beziau and Payette (ред.), The Square of Opposition: A General Framework for Cognition, Peter Lang, Bern, 195-229.
  12. ^ Теория N-оппозиции Логический шестиугольник
  13. ^ Моретти, Пеллиссье

внешняя ссылка