Пропозициональная формула - Propositional formula
В логика высказываний, а пропозициональная формула это тип синтаксического формула который хорошо сформированный и имеет значение истины. Если значения всех переменных в пропозициональной формуле даны, это определяет уникальное значение истинности. Формулу высказываний также можно назвать пропозициональное выражение, а приговор, или сентенциальная формула.
Пропозициональная формула строится из простых предложения, например "пять больше трех" или пропозициональные переменные Такие как п и Q, используя связки или логические операторы например НЕ, И, ИЛИ или ПОДРАЗУМЕВАЕТСЯ; Например:
- (п И НЕТ Q) ПОДРАЗУМЕВАЕТ (п ИЛИ ЖЕ Q).
В математика пропозициональная формула часто более кратко упоминается как "предложение", но, точнее, пропозициональная формула - это не предложение, а формальное выражение который обозначает а предложение, а формальный объект обсуждается, как и такое выражение, как "Икс + у"не является значением, но обозначает значение. В некоторых контекстах сохранение различия может иметь значение.
Предложения
Для целей исчисления высказываний предложения (высказывания, предложения, утверждения) считаются либо просто или же сложный.[1] Сложные предложения считаются связанными сентенциальные связки, некоторые из наиболее распространенных из которых - «И», «ИЛИ», «ЕСЛИ… ТО…», «НИ… НИ…», «… ЭКВИВАЛЕНТНО…». Связывающая точка с запятой «;» и связка «НО» считаются выражениями «И». Считается, что последовательность дискретных предложений связана с помощью «И», и формальный анализ применяет рекурсивный «правило скобок» в отношении последовательностей простых предложений (см. ниже о правильных формулах).
- Например: Утверждение: «Эта корова синего цвета. Эта лошадь оранжевая, а вот эта лошадь фиолетовая». на самом деле является составным утверждением, связанным с помощью «И»: ((«Эта корова синяя» И «эта лошадь оранжевая») И «эта лошадь фиолетовая»).
Простые предложения являются декларативными по своей природе, то есть они содержат утверждения о состоянии или природе частности объект ощущения например «Эта корова синяя», «Это койот!» ("Этот койот ЕСТЬ там, за скалами. ").[2] Таким образом, простой "примитивный" утверждения должны быть о конкретных объектах или определенных состояниях ума. Каждый должен иметь как минимум предмет (непосредственный объект мысли или наблюдения), глагол (предпочтительно в активном голосе и в настоящем времени) и, возможно, прилагательное или наречие. "Собака!" вероятно, подразумевает «Я вижу собаку», но его следует отклонить как слишком двусмысленный.
- Пример: «Эта фиолетовая собака бежит», «Эта корова синяя», «Коммутатор M31 закрыт», «Этот колпачок снят», «Завтра пятница».
Для целей исчисления высказываний сложное предложение обычно можно переформулировать в ряд простых предложений, хотя результат, вероятно, будет звучать неестественно.
Связь пропозициональной формулы и формулы предикатов
В исчисление предикатов идет на шаг дальше, чем исчисление высказываний, к "анализу внутренняя структура предложений »[3] Он разбивает простое предложение на две части (i) его предмет (предмет (единственное число или множественное число) дискурса) и (ii) a предикат (глагол или, возможно, предложение-глагол, которое утверждает качество или атрибут объекта (ов)). Затем исчисление предикатов обобщает форму «субъект | предикат» (где | символизирует конкатенация (объединение) символов) в форму со следующей структурой пустого субъекта «___ | predicate», а предикат, в свою очередь, обобщается на все вещи с этим свойством.
- Пример: «У этой синей свиньи есть крылья» превращается в два предложения в пропозициональное исчисление: «У этой свиньи есть крылья» И «Эта свинья синяя», внутреннее строение которой не рассматривается. Напротив, в исчислении предикатов первое предложение разбивается на «эта свинья» как подлежащее и «имеет крылья» как сказуемое. Таким образом, он утверждает, что объект «эта свинья» является членом класса (набора, коллекции) «крылатых вещей». Во втором предложении утверждается, что объект «эта свинья» имеет атрибут «синий» и, таким образом, является членом класса «синих вещей». Можно записать два предложения, связанных с И, как:
- p | W И p | B
Обобщение «этой свиньи» на (потенциального) члена двух классов «крылатые штуки» и «синие штуки» означает, что у нее есть истинные отношения с обоими этими классами. Другими словами, учитывая область дискурса «крылатые твари», p либо оказывается членом этого домена, либо нет. Таким образом, существует связь W (крылатость) между p (свинья) и {T, F}, W (p) оценивается как {T, F}, где {T, F} - это множество логические значения "правда и ложь". Аналогично для B (голубизна) и p (свинья) и {T, F}: B (p) оценивается как {T, F}. Итак, теперь можно проанализировать связанные утверждения «B (p) AND W (p)» на предмет их общей истинностной ценности, то есть:
- (B (p) AND W (p)) оценивается как {T, F}
В частности, простые предложения, в которых используются понятия «все», «некоторые», «несколько», «одно из» и т. Д., Обрабатываются с помощью исчисления предикатов. Наряду с новым символом функции «F (x)» вводятся два новых символа: ∀ (для всех) и and (существует ..., хотя бы один из ... существует и т. Д.). Исчисление предикатов, но не исчисление высказываний, может установить формальную справедливость следующего утверждения:
- «У всех синих свиней есть крылья, но у некоторых свиней нет крыльев, поэтому некоторые свиньи не синие».
Личность
Тарский утверждает, что понятие ИДЕНТИЧНОСТИ (в отличие от ЛОГИЧЕСКОЙ ЭКВИВАЛЕНТНОСТИ) лежит вне исчисления высказываний; однако он отмечает, что для того, чтобы логика была полезной для математики и наук, она должна содержать «теорию» ИДЕНТИЧНОСТИ.[4] Некоторые авторы ссылаются на «логику предикатов с идентичностью», чтобы подчеркнуть это расширение. Подробнее об этом ниже.
Алгебра предложений, исчисление высказываний
An алгебра (а их много разных), в общих чертах определенный, это метод, с помощью которого набор символы называется переменные вместе с некоторыми другими символами, такими как круглые скобки (,) и некоторым подмножеством символов, таких как *, +, ~, &, ∨, =, ≡, ∧, ¬, обрабатываются внутри система правил. Эти символы и правильно сформированный их строки, как говорят, представляют объекты, но в конкретной алгебраической системе эти объекты не имеют значения. Таким образом, работа внутри алгебры становится упражнением в соблюдении определенных законы (правила) алгебры синтаксис (формирование символа), а не в семантика (значение) символов. Смыслы следует искать вне алгебры.
Для правильной последовательности символов в алгебре - a формула- чтобы иметь некоторую полезность за пределами алгебры, символам присваиваются значения, и в конечном итоге присваиваются переменные значения; то по ряду правил формула оценен.
Когда значения ограничиваются двумя и применяются к понятию простые предложения (например, устные высказывания или письменные утверждения), связанные пропозициональные связки Вся эта алгебраическая система символов, правил и методов оценки обычно называется пропозициональное исчисление или сентенциальное исчисление.
В то время как некоторые из знакомых правил арифметической алгебры продолжают выполняться в алгебре предложений (например, коммутативные и ассоциативные законы для AND и OR), некоторые нет (например, законы распределения для И, ИЛИ и НЕ).
Полезность пропозициональных формул
Анализ: В дедуктивное мышление философы, риторы и математики сводят аргументы к формулам, а затем изучают их (обычно таблицы истинности ) на правильность (разумность). Например: обоснован ли следующий аргумент?
- "Учитывая, что сознания достаточно для искусственный интеллект и только сознательные сущности могут пройти Тест Тьюринга, прежде чем мы сможем сделать вывод, что робот - это искусственный интеллект, он должен пройти тест Тьюринга ".
Инженеры анализируют логические схемы они разработали с использованием методов синтеза, а затем применили различные методы сокращения и минимизации для упрощения своих проектов.
Синтез: В частности, инженеры синтезируют пропозициональные формулы (которые в конечном итоге схемы символов) из таблицы истинности. Например, можно составить таблицу истинности того, как двоичное сложение должен вести себя при добавлении переменных «b» и «a» и «carry_in» «ci», а результаты «carry_out» «co» и «sum» Σ:
- Пример: в строке 5 ((b + a) + ci) = ((1 + 0) + 1) = число «2». записано как двоичное число, это 102, где «co» = 1 и Σ = 0, как показано в крайних правых столбцах.
| ряд | б | а | ci | (b + a) + ci | co | Σ | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 2 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 3 | 0 | 1 | 1 | 2 | 1 | 0 | |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 5 | 1 | 0 | 1 | 2 | 1 | 0 | |
| 6 | 1 | 1 | 0 | 2 | 1 | 0 | |
| 7 | 1 | 1 | 1 | 3 | 1 | 1 |
Пропозициональные переменные
Простейший тип пропозициональной формулы - это пропозициональная переменная. Предложения, которые просты (атомный ), символьные выражения часто обозначаются переменными с именами п, q, или же п, Qи т. д. Пропозициональная переменная предназначена для представления атомарного предложения (утверждения), например, «Сегодня суббота» = п (здесь символ = означает «… присвоена переменная с именем…») или «Я хожу в кино только в понедельник» = q.
Присвоение истинных ценностей, оценка формул
Оценка пропозициональной формулы начинается с присвоения значение истины к каждой переменной. Поскольку каждая переменная представляет собой простое предложение, значения истинности применяются к «истинности» или «ложности» этих простых предложений.
Ценности истины в риторике, философии и математике: Истинных значений всего два: {ИСТИНА "T", ЛОЖЬ "F"}. An эмпирик разделяет все предложения на два широких класса: аналитический- истинно несмотря ни на что (например, тавтология ), и синтетический- получены из опыта и, таким образом, могут быть подтверждены третьими сторонами ( теория проверки смысла).[5] Эмпирики считают, что, как правило, для достижения истинностного значения синтетическое предложение, значения (шаблоны сопоставления с образцом) должны сначала быть применены к словам, а затем эти шаблоны значений должны быть сопоставлены с тем, что утверждается. Например, мое высказывание «Эта корова синий! »Это утверждение - ПРАВДА? Я действительно сказал это. являюсь видение синей коровы - если я не лгу, мое утверждение является ИСТИНОЙ относительно объекта моего (возможно, ошибочного) восприятия. Но действительно ли синяя корова «там»? Что вы видите, когда смотрите в то же окно? Чтобы продолжить проверку, вам потребуется предварительное понятие (шаблон) как "корова", так и "синий", а также способность сопоставлять шаблоны с объектом ощущения (если он действительно существует).[нужна цитата ]
Истинные ценности в инженерии: Инженеры стараются избегать представлений об истине и лжи, которые сбивают с толку философов, но в конечном итоге инженеры должны доверять своим измерительным приборам. В их поисках надежность инженеры предпочитают извлекать известные объекты из небольшой библиотеки - объекты, которые имеют четко определенное, предсказуемое поведение даже в больших комбинациях (отсюда их название для исчисления высказываний: «комбинаторная логика»). Наименьшее количество вариантов поведения одного объекта - два (например, {OFF, ON}, {open, shut}, {UP, DOWN} и т. Д.), И они соответствуют {0, 1}. Такие элементы называются цифровой; те, у кого постоянный диапазон поведения, называются аналог. Всякий раз, когда необходимо принять решение в аналоговой системе, довольно часто инженер преобразует аналоговое поведение (дверь на 45,32146% UP) в цифровое (например, DOWN = 0) с помощью компаратор.[6]
Таким образом, назначение смысл переменных и двух символов-значений {0, 1} поступает "извне" формулы, которая представляет поведение (обычно) составного объекта. Примером может служить дверь гаража с двумя «концевыми выключателями», один для UP, помеченный SW_U, и один для DOWN, помеченный SW_D, и все остальное, что есть в схемах двери. Осмотр схемы (либо схемы, либо самих объектов - двери, переключателей, проводов, печатной платы и т. Д.) Может выявить, что на печатной плате «узел 22» выходит на +0 В, когда контакты переключателя «SW_D» "механически контактируют (" закрыты "), и дверь находится в положении" вниз "(на 95% вниз), а" узел 29 "переходит в +0 В, когда дверь поднята на 95% и контакты переключателя SW_U находятся в в механическом контакте («замкнутый»).[7] Инженер должен определить значения этих напряжений и все возможные комбинации (все 4 из них), включая «плохие» (например, оба узла 22 и 29 на 0 вольт, что означает, что дверь открыта и закрыта одновременно) . Схема бездумно реагирует на любые напряжения, которые она испытывает, не осознавая ИСТИНУ или ЛОЖНОСТЬ, ПРАВИЛЬНО или НЕПРАВИЛЬНО, БЕЗОПАСНО или ОПАСНО.[нужна цитата ]
Пропозициональные связки
Произвольные пропозициональные формулы строятся из пропозициональных переменных и других пропозициональных формул с использованием пропозициональные связки. Примеры связок включают:
- Унарное отрицание связки. Если формула, то это формула.
- Классические бинарные связки . Так, например, если и формулы, так же .
- Другие бинарные связки, такие как NAND, NOR и XOR
- Тернарная связка IF ... THEN ... ELSE ...
- Постоянные 0-арные связки ⊤ и ⊥ (поочередно, константы {T, F}, {1, 0} и т. Д.)
- Связка "теория-расширение" РАВНО (альтернативно, ИДЕНТИЧНОСТЬ или знак "=" в отличие от "логической связки" )
Связки риторики, философии и математики
Ниже приведены общие для риторики, философии и математики связки вместе с их таблицы истинности. Используемые символы будут варьироваться от автора к автору и в зависимости от области деятельности. В общем, сокращения «T» и «F» обозначают оценки ИСТИНА и ЛОЖЬ, применяемые к переменным в формуле высказываний (например, утверждение: «Эта корова синяя» будет иметь значение истинности «T» для Истины или « F "Ложь, в зависимости от обстоятельств.)
Связки имеют множество различных употреблений слов, например «a ПОДРАЗУМЕВАЕТ b» также сказано «ЕСЛИ a ТО b». Некоторые из них показаны в таблице.
| b только если a | |||||||||||
| b Достаточно для | b ТОЧНО, КОГДА a | ||||||||||
| a НЕОБХОДИМ ДЛЯ b | b ЕСЛИ И ТОЛЬКО ЕСЛИ a; б МКФ а | ||||||||||
| включительно ИЛИ | ЕСЛИ b ТО a | b НЕОБХОДИМО И ДОСТАТОЧНО ДЛЯ | |||||||||
| отрицание | отрицание | соединение | дизъюнкция | значение | двухусловный | ||||||
| переменные | НЕ б | НЕ | б И а | b ИЛИ a | b ПОДРАЗУМЕВАЕТ a | b ЕСТЬ логически эквивалентный К *** | f ЯВЛЯЕТСЯ тавтологией | Ни А, ни Б | б ход а | Эксклюзивный или | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| б | а | ¬ (б) | ¬ (а) | (б ∧ а) | (б ∨ а) | (б → а) | (б ↔ а) | (f = формула) | (a NOR b) | (б | а) | разные |
| F | F | Т | Т | F | F | Т | Т | Т | Т | Т | F |
| F | Т | Т | F | F | Т | Т | F | Т | F | Т | Т |
| Т | F | F | Т | F | Т | F | F | Т | F | Т | Т |
| Т | Т | F | F | Т | Т | Т | Т | Т | F | F | F |
Инженерные соединители
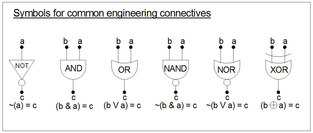
В общем, инженерные связки такие же, как и математические связки, за исключением того, что они обычно оцениваются как «1» = «T» и «0» = «F». Это делается с целью анализа / минимизации и синтеза формул с использованием понятия минтермы и Карты Карно (Смотри ниже). Инженеры также используют слова логический продукт из Логический понятие (a * a = a) и логическая сумма из Джевонс понятие (а + а = а).[8]
| логический продукт | логическая сумма | полусумматор (без переноса) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Эксклюзивный или | |||||||||
| номер строки | переменные | НЕТ | НЕТ | И | ИЛИ ЖЕ | NAND | НИ | XOR | |
| Би 21+ а * 20 | б | а | ~ (б) | ~ (а) | (b & a) | (б ∨ а) | ~ (b & a) | ~ (b ∨ a) | ⊕ |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
CASE связующее: ЕСЛИ… ТО… ИНАЧЕ…
Связка IF ... THEN ... ELSE ... появляется как простейшая форма оператора CASE для теория рекурсии и теория вычислений и является связкой, отвечающей за условные переходы (переходы, ветки). Из этой одной связки могут быть построены все остальные связки (подробнее см. Ниже). Хотя «IF c THEN b ELSE a» звучит как импликация, в наиболее сокращенной форме это выключатель который принимает решение и предлагает в качестве результата только одну из двух альтернатив «a» или «b» (отсюда и название оператор переключения в C язык программирования).[9]
Следующие три предложения эквивалентны (на что указывает знак логической эквивалентности ≡):
- (ЕСЛИ 'счетчик равен нулю' ТО 'перейти к инструкции б 'ELSE' перейти к инструкции а ') ≡
- ((c → b) & (~ c → a)) ≡ ((IF 'counter равен нулю' THEN 'перейти к инструкции б ') И (ЕСЛИ' Это НЕ тот случай, когда счетчик равен нулю 'ТОГДА перейти к инструкции а ) " ≡
- ((c & b) ∨ (~ c & a)) ≡ "('Счетчик равен нулю' И 'перейти к инструкции б ) ИЛИ ('Это НЕ тот случай, когда' счетчик равен нулю 'И' перейти к инструкции а ) "
Таким образом, IF… THEN… ELSE - в отличие от импликации - не оценивается как двусмысленная «ИСТИНА», когда первое утверждение ложно, то есть c = F in (c → b). Например, большинство людей отвергло бы следующее сложное утверждение как бессмысленное. non sequitur потому что второе предложение не связаны по смыслу к первому.[10]
- Пример: Утверждение «ЕСЛИ Уинстон Черчилль был китайцем, ТО« Солнце восходит на востоке »» оценивается как ИСТИНА, учитывая, что «Уинстон Черчилль был китайцем» - ЛОЖЬ, а «Солнце восходит на востоке» оценивается как ИСТИНА .
Признавая эту проблему, знак → формальной импликации в исчислении высказываний называется материальное значение чтобы отличить это от обыденного, интуитивного подтекста.[11]
Использование конструкции IF ... THEN ... ELSE позволяет избежать противоречий, поскольку предлагает полностью детерминированный выбор между двумя заявленными альтернативами; он предлагает два "объекта" (две альтернативы b и a), и выбирает между ними исчерпывающе и однозначно.[12] В приведенной ниже таблице истинности d1 - это формула: ((IF c THEN b) AND (IF NOT-c THEN a)). Его полностью сокращенная форма d2 - это формула: ((c AND b) OR (NOT-c AND a). Эти две формулы эквивалентны, как показано в столбцах «= d1» и «= d2». Инженеры-электрики называют полностью сокращенный формула оператора AND-OR-SELECT. Оператор CASE (или SWITCH) является расширением той же идеи для п возможные, но взаимоисключающие исходы. Инженеры-электрики называют оператора CASE мультиплексор.
| d1 | d2 | ||||||||||||||||||||||||||||||||||||||
| ряд | c | б | а | ( | ( | c | → | б | ) | & | ( | ~ | ( | c | ) | → | а | ) | ) | = d1 | ( | ( | c | & | б | ) | ∨ | ( | ~ | ( | c | ) | & | а | ) | ) | = d2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 3 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||||||||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||||||||||||||||||
| 6 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | ||||||||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
ИДЕНТИЧНОСТЬ и оценка
Первая таблица этого раздела помечена *** логической эквивалентностью записи, чтобы отметить тот факт, что "Логическая эквивалентность "- это не то же самое, что" идентичность ". Например, большинство согласятся, что утверждение" Эта корова синяя "идентично утверждению" Эта корова синяя ". С другой стороны, логичный эквивалентность иногда появляется в речи, как в этом примере: «« Солнце светит »означает« Я еду на велосипеде »». В переводе в формулу предложения эти слова становятся такими: «ЕСЛИ« солнце светит »ТОГДА« Я еду на велосипеде », И ЕСЛИ «Я еду на велосипеде», ТО «светит солнце»:[13]
- «IF 's' THEN 'b' AND IF 'b' THEN 's'» записывается как ((s → b) & (b → s)) или в сокращенной форме как (s ↔ b). Поскольку самая правая строка символов - это определение для нового символа в терминах символов слева подходит использование знака ИДЕНТИЧНОСТЬ =:
- ((s → b) & (b → s)) = (s ↔ b)
Разные авторы используют разные знаки для логической эквивалентности: ↔ (например, Suppes, Гудштейн, Гамильтон), ≡ (например, Роббин), ⇔ (например, Бендер и Уильямсон). Обычно идентичность записывается как знак равенства =. Одно исключение из этого правила находится в Principia Mathematica. Подробнее о философии понятия ИДЕНТИЧНОСТЬ см. Закон Лейбница.
Как отмечалось выше, Тарский считает, что ИДЕНТИЧНОСТЬ лежит за пределами исчисления высказываний, но он утверждает, что без понятия «логика» недостаточна для математики и дедуктивных наук. Фактически, знак входит в исчисление высказываний, когда формула должна быть вычислена.[14]
В некоторых системах нет таблиц истинности, а есть только формальные аксиомы (например, строки символов из набора {~, →, (,), переменных p1, п2, п3, ...} и правила формирования формул (правила о том, как сделать больше символьных строк из предыдущих строк, используя, например, замену и modus ponens ). результатом такого исчисления будет другая формула (то есть правильно сформированная строка символов). В конце концов, однако, если кто-то хочет использовать исчисление для изучения понятий достоверности и истины, необходимо добавить аксиомы, которые определяют поведение символов, называемых «значениями истинности» {T, F} (или {1, 0} и т. Д. .) относительно других символов.
Например, Гамильтон использует два символа = и ≠, когда определяет понятие оценка v любой правильные формулы (wffs) А и B в его «исчислении формальных утверждений» L. v это функция от wffs его системы L до диапазона (выхода) {T, F}, учитывая, что каждая переменная p1, п2, п3 в wff присваивается произвольное значение истинности {T, F}.
- v(А) ≠ v(~А)
(я)
- v(А → B) = F тогда и только тогда, когда v(А) = T и v(B) = F
(ii)
Два определения (я) и (ii) определяют эквивалент таблиц истинности для связок ~ (НЕ) и → (ИМПЛИКАЦИЯ) его системы. Первый выводит F ≠ T и T ≠ F, другими словами " v(А) не иметь в виду v(~А)". Определение (ii) указывает третью строку в таблице истинности, а остальные три строки затем берутся из приложения определения (я). Особенно (ii) назначает значение F (или значение «F») для всего выражения. Определения также служат в качестве правил формирования, которые позволяют заменять ранее полученное значение в формулу:
| v (А → В) | ||||
| ( | v (А) | → | v (B) | ) |
| F | Т | F | ||
| F | Т | Т | ||
| Т | F | F | ||
| Т | Т | Т |
Немного формальные системы определите эти аксиомы оценки с самого начала в виде определенных формул, таких как закон противоречия или законы идентичности и недействительности. Выбор того, какие из них использовать, вместе с такими законами, как коммутация и распределение, остается за разработчиком системы, если набор аксиом задан. полный (т.е. достаточно, чтобы сформировать и оценить любую правильно сформированную формулу, созданную в системе).
Более сложные формулы
Как показано выше, связка CASE (IF c THEN b ELSE a) создается либо из двух аргументов IF ... THEN ... и AND, либо из OR и AND и 1-аргумента NOT. Соединительные элементы, такие как n-аргумент AND (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n), состоят из строк с двумя аргументами AND и OR и записываются в сокращенная форма без скобок. Эти и другие связки можно затем использовать в качестве строительных блоков для создания новых связок. Риторики, философы и математики используют таблицы истинности и различные теоремы для анализа и упрощения своих формул.
Электротехника использует нарисованные символы и соединяет их линиями, обозначающими математический акт замена и замена. Затем они сверяют свои рисунки с таблицами истинности и упрощают выражения, как показано ниже, с помощью Карты Карно или теоремы. Таким образом, инженеры создали множество «комбинаторной логики» (то есть соединений без обратной связи), таких как «декодеры», «кодеры», «многофункциональные вентили», «мажоритарная логика», «двоичные сумматоры», «арифметические логические блоки», и Т. Д.
Определения
Определение создает новый символ и его поведение, часто в целях сокращения. После представления определения можно использовать любую форму эквивалентного символа или формулы. Следующий символизм =Df следует соглашению Райхенбаха.[15] Некоторые примеры удобных определений, взятых из набора символов {~, &, (,)} и переменных. Каждое определение порождает логически эквивалентную формулу, которую можно использовать для замены или замены.
- определение новой переменной: (c & d) =Df s
- ИЛИ: ~ (~ a & ~ b) =Df (а ∨ б)
- ПОСЛЕДСТВИЕ: (~ a ∨ b) =Df (а → б)
- ИСКЛЮЧАЮЩЕЕ ИЛИ: (~ a & b) ∨ (a & ~ b) =Df (а ⊕ б)
- ЛОГИЧЕСКАЯ ЭКВИВАЛЕНТНОСТЬ: ((a → b) & (b → a)) =Df (а ≡ б)
Аксиома и определение схемы
Приведенные выше определения OR, IMPLICATION, XOR и логической эквивалентности на самом деле схемы (или "схемы"), то есть они модели (демонстрации, примеры) для общей формулы формат но показаны (в иллюстративных целях) с конкретными буквами a, b, c для переменных, тогда как любые буквы переменных могут занимать свои места, если замены букв следуют правилу замены, приведенному ниже.
- Пример: в определении (~ a ∨ b) =Df (a → b), могут использоваться другие символы-переменные, такие как "SW2" и "CON1", т.е. формально:
- а =Df SW2, b =Df CON1, поэтому в качестве пример схемы определения (~ SW2 ∨ CON1) =Df (SW2 → CON1)
Замена против замены
Замена: Переменная или подформула, которую нужно заменить другой переменной, константой или подформулой, должна быть заменена во всех случаях во всей формуле.
- Пример: (c & d) ∨ (p & ~ (c & ~ d)), но (q1 & ~ q2) ≡ d. Теперь везде, где встречается переменная "d", подставьте (q1 & ~ q2):
- (c & (q1 & ~ q2)) ∨ (p & ~ (c & ~ (q1 & ~ q2)))
Замена: (i) заменяемая формула должна находиться в тавтологии, т.е. логически эквивалентный (связанный с помощью ≡ или ↔) с заменяющей его формулой, и (ii) в отличие от замены его допустимо, чтобы замена происходила только в одном месте (то есть для одной формулы).
- Пример: используйте этот набор схем / эквивалентов формул:
- ((а ∨ 0) ≡ а).
- ((a & ~ a) ≡ 0).
- ((~ a ∨ b) =Df (а → б)).
- (~ (~ а) ≡ а)
- начать с "а": а
- Используйте 1, чтобы заменить "a" на (a 0): (a ∨ 0)
- Используйте понятие «схема», чтобы заменить b на a в 2: ((a & ~ a)) 0)
- Используйте 2, чтобы заменить 0 на (b & ~ b): (a ∨ (b & ~ b))
- (см. ниже, как распределить "a ∨" по (b & ~ b) и т. д.)
Индуктивное определение
Классическое представление логики высказываний (см. Enderton 2002) использует связки . Набор формул для данного набора пропозициональных переменных есть индуктивно определенный быть наименьшим набором выражений, таких что:
- Каждая пропозициональная переменная в наборе представляет собой формулу,
- формула всякий раз, когда есть, и
- формула всякий раз, когда и формулы и одна из бинарных связок .
Это индуктивное определение может быть легко расширено на дополнительные связки.
Индуктивное определение также можно перефразировать в терминах закрытие операция (Enderton 2002). Позволять V обозначим набор пропозициональных переменных и пусть ИксV обозначают набор всех строк из алфавита, включая символы в V, левая и правая круглые скобки и все рассматриваемые логические связки. Каждая логическая связка соответствует операции построения формулы, функции из XXV к XXV:
- Учитывая строку z, операция возвращается .
- Данные строки у и z, операция возвращается . Есть похожие операции , , и соответствующие другим двоичным связкам.
Набор формул над V определяется как наименьшее подмножество XXV содержащий V и закрыт по всем операциям построения формулы.
Формулы парсинга
Следующие «законы» исчисления высказываний используются для «сведения» сложных формул. «Законы» можно легко проверить с помощью таблиц истинности. Для каждого закона главная (самая внешняя) связка связана с логической эквивалентностью ≡ или тождеством =. Полный анализ всех 2п комбинации истинностных ценностей для п Различные переменные приведут к столбцу единиц (Т) под этой связкой. Это открытие делает каждый закон по определению тавтологией. И для данного закона, поскольку его формула слева и справа эквивалентны (или идентичны), они могут быть заменены друг на друга.
- Пример: Следующая таблица истинности представляет собой закон Де Моргана для поведения НЕ над ИЛИ: ~ (a ∨ b) ≡ (~ a & ~ b). Слева от главной связки ≡ (желтый столбец с надписью «туго натянутый») формула ~ (b ∨ a) оценивается как (1, 0, 0, 0) под меткой «P». Справа от «натянуто» формула (~ (b) ∨ ~ (a)) также оценивается как (1, 0, 0, 0) под меткой «Q». Поскольку два столбца имеют эквивалентные оценки, логическая эквивалентность ≡ под "натянутым" оценивается как (1, 1, 1, 1), то есть P ≡ Q. Таким образом, любая формула может быть заменена другой, если она появляется в более крупной формуле.
| п | натянутый | Q | ||||||||||||||||||||
| б | а | ( | ~ | ( | б | V | а | ) | ≡ | ( | ~ | ( | б | ) | & | ~ | ( | а | ) | ) | ) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |||||||||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |||||||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Предприимчивые читатели могут бросить вызов себе изобрести «аксиоматическую систему», которая использует символы {∨, &, ~, (,), переменные a, b, c}, правила формирования, указанные выше, и как можно меньше перечисленных законов. ниже, а затем вывести как теоремы другие, а также оценки таблицы истинности для, & и ~. Один набор, приписываемый Хантингтону (1904) (Suppes: 204), использует восемь законов, определенных ниже.
При использовании в аксиоматической системе символы 1 и 0 (или T и F) считаются правильно построенными формулами и, таким образом, подчиняются всем тем же правилам, что и переменные. Таким образом, перечисленные ниже законы на самом деле схемы аксиом, то есть они заменяют бесконечное количество экземпляров. Таким образом, (x ∨ y) ≡ (y ∨ x) может использоваться в одном случае, (p ∨ 0) ≡ (0 ∨ p), а в другом случае (1 ∨ q) ≡ (q ∨ 1) и т. Д.
Соединительный стаж (символ ранга)
В общем, чтобы избежать путаницы при анализе и оценке пропозициональных формул, широко используйте круглые скобки. Однако довольно часто авторы не учитывают их. Чтобы разобрать сложную формулу, сначала нужно знать старшинство, или же классифицировать, что каждая из связок (кроме *) имеет по сравнению с другими связками. Чтобы «правильно сформировать» формулу, начните с связки с наивысшим рангом и добавьте скобки вокруг ее компонентов, затем двигайтесь вниз по рангу (обращая особое внимание на связку объем над которым он работает). От старшего к старшему, с предикатными знаками ∀x и ∃x, ИДЕНТИЧНОСТЬ = и арифметические знаки добавляются для полноты:[16]
- ≡
- (ЛОГИЧЕСКОЕ ЭКВИВАЛЕНТНОСТЬ)
- →
- (ПОСЛЕДСТВИЕ)
- &
- (И)
- ∨
- (ИЛИ ЖЕ)
- ~
- (НЕТ)
- ∀x
- (ДЛЯ ВСЕХ x)
- ∃x
- (ЕСТЬ СУЩЕСТВУЕТ x)
- =
- (ЛИЧНОСТЬ)
- +
- (арифметическая сумма)
- *
- (арифметическое умножение)
- '
- (s, арифметический преемник).
Таким образом, формула может быть проанализирована, но поскольку NOT не подчиняется закону распределения, круглые скобки вокруг внутренней формулы (~ c & ~ d) являются обязательными:
- Пример: "d & c ∨ w" переписывается как ((d & c) ∨ w)
- Пример: «a & a → b ≡ a & ~ a ∨ b» переписывается (строго) и
- ≡ имеет стаж: ((a & a → b) ≡ (a & ~ a ∨ b))
- → имеет стаж: ((a & (a → b)) ≡ (a & ~ a ∨ b))
- & имеет старшинство с обеих сторон: ((((a) & (a → b))) ≡ (((a) & (~ a ∨ b)))
- ~ имеет стаж: ((((a) & (a → b))) ≡ (((a) & (~ (a) ∨ b)))
- проверьте 9 (- скобки и 9) - скобки: ((((a) & (a → b))) ≡ (((a) & (~ (a) ∨ b)))
- Пример:
- d & c ∨ p & ~ (c & ~ d) ≡ c & d ∨ p & c ∨ p & ~ d переписывается как (((d & c) ∨ (p & ~ ((c & ~ (d))) )) ≡ ((c & d) ∨ (p & c) ∨ (p & ~ (d))))
Коммутативные и ассоциативные законы
И И, и ИЛИ подчиняются коммутативный закон и ассоциативный закон:
- Коммутативный закон для OR: (a ∨ b) ≡ (b ∨ a)
- Коммутативный закон для AND: (a & b) ≡ (b & a)
- Ассоциативный закон для ИЛИ: ((a ∨ b) ∨ c) ≡ (a ∨ (b ∨ c))
- Ассоциативный закон для AND: ((a & b) & c) ≡ (a & (b & c))
Опускание скобок в строках AND и OR: Связки считаются унарными (с одной переменной, например, NOT) и двоичными (то есть с двумя переменными AND, OR, IMPLIES). Например:
- ((c & d) ∨ (p & c) ∨ (p & ~ d)) выше должно быть написано (((c & d) ∨ (p & c)) ∨ (p & ~ (d))) или, возможно, ((c & d) ∨ ((p & c) ∨ (p & ~ (d))))
Однако демонстрация таблицы истинности показывает, что форма без лишних скобок вполне подходит.
Пропуск круглых скобок в отношении одной переменной NOT: Хотя ~ (a), где a - единственная переменная, совершенно ясно, ~ a подходит и обычно буквальный представляется. Когда НЕ стоит над формулой с более чем одним символом, скобки обязательны, например ~ (a ∨ b).
Распределительные законы
ИЛИ распределяет по И, а И распределяет по ИЛИ. НЕ распространяется по И или ИЛИ. См. Ниже о законе Де Моргана:
- Распределительный закон для OR: (c ∨ (a & b)) ≡ ((c ∨ a) & (c ∨ b))
- Распределительный закон для AND: (c & (a ∨ b)) ≡ ((c & a) ∨ (c & b))
Законы де Моргана
НЕ при распределении по ИЛИ или И делает что-то особенное (опять же, это можно проверить с помощью таблицы истинности):
- Закон Де Моргана для OR: ¬ (a ∨ b) ≡ (¬a ^ ¬b)
- Закон Де Моргана для AND: ¬ (a ^ b) ≡ (¬a ∨ ¬b)
Законы абсорбции
Поглощение, в частности первое, заставляет «законы» логики отличаться от «законов» арифметики:
- Поглощение (идемпотентность) для OR: (a ∨ a) ≡ a
- Поглощение (идемпотентность) для AND: (a & a) ≡ a
Законы оценки: идентичность, недействительность и дополнение
Знак «=» (в отличие от логической эквивалентности ≡, попеременно ↔ или ⇔) символизирует присвоение значения или значения. Таким образом, строка (a & ~ (a)) символизирует "0", т.е. средства то же самое, что и символ «0». В некоторых «системах» это будет аксиома (определение), возможно, показанная как ((a & ~ (a)) =Df 0); в других системах его можно получить из приведенной ниже таблицы истинности:
| c | натянутый | c | |||||||||||
| а | ( | ( | а | & | ~ | ( | а | ) | ) | ≡ | 0 | ) | |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | |||||||
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
- Коммутация равенства: (a = b) ≡ (b = a)
- Тождество для ИЛИ: (a ∨ 0) = a или (a ∨ F) = a
- Идентичность для AND: (a & 1) = a или (a & T) = a
- Обнуление для OR: (a ∨ 1) = 1 или (a ∨ T) = T
- Обнуление для AND: (a & 0) = 0 или (a & F) = F
- Дополнение к OR: (a ∨ ~ a) = 1 или (a ∨ ~ a) = T, закон исключенного среднего
- Дополнение для AND: (a & ~ a) = 0 или (a & ~ a) = F, закон противоречия
Двойной отрицательный (инволюция)
- ¬ (¬a) ≡ а
Правильные формулы (wffs)
Ключевым свойством формул является то, что они могут быть однозначно проанализированы для определения структуры формулы с точки зрения ее пропозициональных переменных и логических связок. Когда формулы записываются в инфиксная запись Как и выше, уникальная удобочитаемость обеспечивается соответствующим использованием круглых скобок в определении формул. Как вариант, формулы можно записать в Польская нотация или же обратная польская запись, полностью устраняя необходимость в скобках.
Индуктивное определение инфиксных формул в предыдущем разделе можно преобразовать в формальная грамматика в Форма Бэкуса-Наура:
<формула> ::= <пропозициональная переменная>| ( ¬ <формула> )| ( <формула> ∧ <формула>)| ( <формула> ∨ <формула> )| ( <формула> → <формула> )| ( <формула> ↔ <формула> )Можно показать, что любое выражение, соответствующее грамматике, имеет сбалансированное количество левых и правых скобок, а любой непустой начальный сегмент формулы имеет больше левых, чем правых скобок.[17] Этот факт можно использовать, чтобы дать алгоритм разбора формул. Например, предположим, что выражение Икс начинается с . Начиная со второго символа, сопоставьте самое короткое подвыражение у из Икс со сбалансированными круглыми скобками. Если Икс - формула, после этого выражения остается ровно один символ, этот символ - закрывающая скобка, и у сама по себе формула. Эта идея может быть использована для создания парсер рекурсивного спуска для формул.
Пример подсчета скобок:
Этот метод определяет как "1" основная связка - связка, под которой происходит общая оценка формулы для крайних скобок (которые часто опускаются).[18] Он также находит самую внутреннюю связку, с которой можно было бы начать вычисление формулы без использования таблицы истинности, например на «уровне 6».
| Начните | ( | ( | ( | c | & | d | ) | V | ( | п | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | = | ( | ( | ( | c | & | d | ) | V | ( | п | & | d | ) | ) | V | ( | п | & | ~ | ( | c | ) | ) | ) | ) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| считать | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 5 | 4 | 3 | 3 | 1 | 1 | 2 | 3 | 4 | 4 | 4 | 4 | 3 | 3 | 4 | 4 | 4 | 4 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 1 | 0 |
Правильно сформированные формулы и действительные формулы в выводах
Понятие действительный аргумент обычно применяется к выводы в аргументах, но аргументы сводятся к пропозициональным формулам и могут быть оценены так же, как и любые другие пропозициональные формулы. Здесь действительный вывод означает: «Формула, представляющая вывод, оценивается как« истина »ниже своей основной связки, независимо от того, какие истинностные значения присваиваются ее переменным», то есть формула является тавтологией.[19]Вполне возможно, что формула будет правильно сформированный но нет действительный. Другой способ сказать это: «Быть хорошо сформированным - значит необходимо чтобы формула действовала, но это не так достаточный. "Единственный способ узнать, обе правильно сформированный и действительным является его проверка с помощью таблицы истинности или с использованием «законов»:
- Пример 1. Что можно сказать о следующем утверждении, которому трудно следовать? Это действительно так? «Если солнечно, но если лягушка квакает, значит, не солнечно, то это все равно, что сказать, что лягушка не квакает». Преобразуйте это в пропозициональную формулу следующим образом:
- "ЕСЛИ (a И (ЕСЛИ b ТО НЕ-a) ТО НЕ-a", где "a" представляет "ее солнечный свет", а "b" представляет "лягушка квакает":
- (((a) & ((b) → ~ (a)) ≡ ~ (b))
- Это правильно, но так ли это? действительный? Другими словами, при вычислении будет ли это давать тавтологию (все T) под символом логической эквивалентности ≡? Ответ НЕТ, это недействительно. Однако если реконструировать как значение тогда аргумент является действительный.
- "Говорят, солнечно, а если лягушка квакает, значит, не солнечно, подразумевает что лягушка не квакает ".
- Квакать лягушке могут и другие обстоятельства: возможно, ее съел журавль.
- Пример 2 (от Райхенбаха через Бертрана Рассела):
- «Если у свиней есть крылья, некоторых крылатых животных можно есть. Некоторых крылатых животных можно есть, поэтому у свиней есть крылья».
- (((a) → (b)) & (b) → (a)) правильно сформирован, но недопустимый аргумент, как показано красной оценкой под основным импликацией:
| W | грамм | аргумент | |||||||||||||
| а | б | ( | ( | ( | а | -> | б | ) | & | б | ) | -> | а | ) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Уменьшенные наборы связок

Набор логических связок называется полный если каждая пропозициональная формула тавтологически эквивалентна формуле только со связками в этом наборе. Есть много полных наборов связок, в том числе , , и . Есть две бинарные связки, которые завершаются сами по себе, соответствующие NAND и NOR соответственно.[20] Некоторые пары не полные, например .
Ход (NAND)
Бинарная связка, соответствующая NAND, называется Инсульт Шеффера, и написано с вертикальной чертой | или вертикальная стрелка ↑. Полнота этой связки отмечена в Principia Mathematica (1927: xvii). Поскольку он сам по себе завершен, все остальные связки можно выразить с помощью только штриха. Например, где символ "≡" представляет логическая эквивалентность:
- ~ p ≡ p | p
- р → д р | ~ д
- p ∨ q ≡ ~ p | ~ q
- p & q ≡ ~ (p | q)
В частности, нулевые связки (представляя истину) и (представляющий ложность) можно выразить с помощью штриха:
ЕСЛИ… ТО… ИНАЧЕ
Эта связка вместе с {0, 1}, (или {F, T} или { , }) образует полный набор. Далее IF ... THEN ... ELSE связь (c, b, a) = d представляет ((c → b) ∨ (~ c → a)) ≡ ((c & b) ∨ (~ c & a)) = d
- (в, б, а):
- (c, 0, 1) ≡ ~ c
- (c, b, 1) ≡ (c → b)
- (c, c, a) ≡ (c ∨ a)
- (c, b, c) ≡ (c и b)
Пример: Ниже показано, как будет проходить основанное на теореме доказательство «(c, b, 1) ≡ (c → b)», ниже доказательства - его проверка таблицы истинности. (Примечание: (c → b) - это определенный быть (~ c ∨ b)):
- Начните с сокращенной формы: ((c & b) ∨ (~ c & a))
- Замените "1" на a: ((c & b) ∨ (~ c & 1))
- Идентичность (~ c & 1) = ~ c: ((c & b) ∨ (~ c))
- Закон коммутации для V: ((~ c) ∨ (c & b))
- Распределите "~ c V" по (c и b): (((~ c) ∨ c) & ((~ c) ∨ b)
- Закон исключенной середины (((~ c) ∨ c) = 1): ((1) & ((~ c) ∨ b))
- Распределите "(1) &" по ((~ c) ∨ b): (((1) & (~ c)) ∨ ((1) & b)))
- Коммутивность и идентичность ((1 & ~ c) = (~ c & 1) = ~ c, и ((1 & b) ≡ (b & 1) ≡ b: (~ c ∨ b)
- (~ c ∨ b) определяется как c → b К. Э. Д.
В следующей таблице истинности столбец, помеченный как «натянутый» для тавтологии, оценивает логическая эквивалентность (обозначается здесь ≡) между двумя столбцами, обозначенными d. Поскольку все четыре строки под словом «натянуто» равны 1, эквивалентность действительно представляет собой тавтологию.
| d | натянутый | d | |||||||||||||||||||||||||||||
| ряды | c | б | а | ( | ( | ( | c | & | б | ) | V | ( | ~ | ( | c | ) | & | а | ) | ) | ≡ | ( | ~ | ( | c | ) | V | б | ) | ) | |
| 0,1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |||||||||||||||
| 2,3 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | |||||||||||||||
| 4,5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |||||||||||||||
| 6,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
Нормальные формы
Произвольная пропозициональная формула может иметь очень сложную структуру. Часто бывает удобно работать с формулами, имеющими более простые формы, известные как нормальные формы. Некоторые общие нормальные формы включают: конъюнктивная нормальная форма и дизъюнктивная нормальная форма. Любая пропозициональная формула может быть приведена к конъюнктивной или дизъюнктивной нормальной форме.
Приведение к нормальной форме

Приведение к нормальной форме относительно просто, если подготовлена таблица истинности формулы. Но дальнейшие попытки минимизировать количество литералы (см. ниже) требует некоторых инструментов: редукции по законам Де Моргана и таблицы истинности может быть громоздким, но Карты Карно очень подходят небольшое количество переменных (5 или меньше). Некоторые сложные табличные методы существуют для более сложных схем с несколькими выходами, но они выходят за рамки данной статьи; подробнее см. Алгоритм Куайна – Маккласки.
Буквальный, термин и альтернативный
В электротехнике переменная x или ее отрицание ~ (x) объединяются в одно понятие, называемое буквальный. Строка литералов, соединенных оператором AND, называется срок. Строка литералов, соединенных ИЛИ, называется альтерм. Обычно литерал ~ (x) сокращается до ~ x. Иногда & -символ вообще опускается в порядке алгебраического умножения.
- Примеры
- a, b, c, d - переменные. (((a & ~ (b)) & ~ (c)) & d) - это термин. Это может быть сокращено как (a & ~ b & ~ c & d) или a ~ b ~ cd.
- p, q, r, s - переменные. (((p & ~ (q)) & r) & ~ (s)) - это альтернатива. Это может быть сокращено как (p ∨ ~ q ∨ r ∨ ~ s).
Минтермс
Так же, как и 2п-row таблица истинности отображает оценку пропозициональной формулы для всех 2п возможных значений его переменных, n переменных дает 2п-квадратная карта Карно (хотя мы не можем нарисовать ее в полномерной реализации). Например, 3 переменных дают 23 = 8 рядов и 8 квадратов Карно; 4 переменные дают 16 строк таблицы истинности и 16 квадратов и, следовательно, 16 минтермы. Каждый квадрат карты Карно и соответствующая ему оценка таблицы истинности представляют один минтерм.
Любая пропозициональная формула может быть сведена к «логической сумме» (ИЛИ) активных (то есть со значением «1» или «Т») минтермов. Когда в этой форме формула, как говорят, находится в дизъюнктивная нормальная форма. Но даже несмотря на то, что он находится в такой форме, он не обязательно минимизирован в отношении количества терминов или количества литералов.
В следующей таблице обратите внимание на особую нумерацию строк: (0, 1, 3, 2, 6, 7, 5, 4, 0). Первый столбец является десятичным эквивалентом двоичного эквивалента цифр cba, другими словами:
- Пример
- cba2 = с * 22 + b * 21 + а * 20:
- cba = (c = 1, b = 0, a = 0) = 1012 = 1*22 + 0*21 + 1*20 = 510
Такая нумерация возникает из-за того, что при перемещении по таблице от строки к строке только одна переменная за раз изменяет свое значение. Код Грея выводится из этого понятия. Это понятие можно распространить на трехмерные и четырехмерные гиперкубы называется Диаграммы Хассе где переменные каждого угла изменяются только по одной за раз при перемещении по краям куба. Диаграммы Хассе (гиперкубы), сплющенные в два измерения, либо Диаграммы Вейча или же Карты Карно (это практически одно и то же).
При работе с картами Карно всегда нужно помнить, что верхний край «огибает» нижний край, а левый - правый - диаграмма Карно действительно трехмерная, четырех- или n-мерная. сплющенный объект.
| десятичный эквивалент (c, b, a) | c | б | а | минтерм |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | (~ c & ~ b & ~ a) |
| 1 | 0 | 0 | 1 | (~ c & ~ b & a) |
| 3 | 0 | 1 | 1 | (~ c & b & a) |
| 2 | 0 | 1 | 0 | (~ c & b & ~ a) |
| 6 | 1 | 1 | 0 | (c & b & ~ a) |
| 7 | 1 | 1 | 1 | (c & b & a) |
| 5 | 1 | 0 | 1 | (c & ~ b & a) |
| 4 | 1 | 0 | 0 | (c & ~ b & ~ a) |
| 0 | 0 | 0 | 0 | (~ a & ~ b & ~ c) |
Сокращение с использованием метода карты (Veitch, Karnaugh)
Вейч улучшил понятие Диаграммы Венна путем преобразования кругов в прилегающие квадраты, а Карно упростил диаграмму Вейча, преобразовав минтермы, записанные в их буквальной форме (например, ~ abc ~ d), в числа.[21] Метод работает следующим образом:
Составьте таблицу истинности формулы
Составьте таблицу истинности формулы. Пронумеруйте его строки, используя двоичные эквиваленты переменных (обычно просто последовательно от 0 до n-1) для n переменных.
- Технически пропозициональная функция был приведен к своей (не минимизированной) конъюнктивной нормальной форме: каждая строка имеет свое выражение minterm, и их можно объединить с помощью ИЛИ, чтобы получить формулу в ее (не минимизированной) конъюнктивной нормальной форме.
Пример: ((c & d) ∨ (p & ~ (c & (~ d)))) = q в конъюнктивной нормальной форме:
- ((~ p & d & c) ∨ (p & d & c) ∨ (p & d & ~ c) ∨ (p & ~ d & ~ c)) = q
Однако эта формула может быть уменьшена как по количеству членов (с 4 до 3), так и по общему количеству ее литералов (с 12 до 6).
| ряд | Минтермс | п | d | c | ( | ( | c | & | d | ) | ∨ | ( | п | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | Активные минтермы | Формула в соединительной нормальной форме |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (~ p & ~ d & ~ c) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ||||||||||||||
| 1 | (~ p & ~ d & c) | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 2 | (~ p & d & ~ c) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||||||||||||||
| 3 | (~ p & d & c) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | (~ p & d & c) | |||||||||||||
| 4 | (p & ~ d & ~ c) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | (~ p & d & c) | |||||||||||||
| 5 | (p & ~ d & c) | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 6 | (p & d & ~ c) | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | (p & d & ~ c) | |||||||||||||
| 7 | (p & d & c) | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | (p & d & c) | |||||||||||||
| q | = (~ p & d & c) ∨ (~ p & d & c) ∨ (p & d & ~ c) ∨ (p & d & c) |
Создайте карту Карно формулы

Используйте значения формулы (например, "p"), найденные методом таблицы истинности, и поместите их в их соответствующие (связанные) квадраты Карно (они пронумерованы в соответствии с соглашением о кодах Грея). Если в таблице появляются значения «d» для «безразлично», это добавляет гибкости на этапе сокращения.
Уменьшить минтермы
Минтермы соседних (примыкающих) 1-квадратов (Т-квадратов) можно уменьшить по количеству их литералы, и количество членов также будет сокращено в процессе. Два примыкающих квадрата (2 x 1 по горизонтали или 1 x 2 по вертикали, даже края представляют собой примыкающие квадраты) теряют один буквальный, четыре квадрата в прямоугольнике 4 x 1 (горизонтальном или вертикальном) или квадрате 2 x 2 (даже четыре угла представляют примыкающие друг к другу квадраты) теряют два литерала, восемь квадратов в прямоугольнике теряют 3 литерала и т. д. (Один ищет самый большой квадрат или прямоугольники и игнорирует меньшие квадраты или прямоугольники, полностью содержащиеся в нем.) Этот процесс продолжается до тех пор, пока не будут учтены все примыкающие квадраты, в этот момент пропозициональная формула сводится к минимуму.
Например, квадраты №3 и №7 упираются. Эти два смежных квадрата могут потерять один литерал (например, «p» из квадратов №3 и №7), четыре квадрата в прямоугольнике или квадрате теряют два литерала, восемь квадратов в прямоугольнике теряют 3 литерала и т. Д. (Один ищет самый большой квадрат или прямоугольники.) Этот процесс продолжается до тех пор, пока не будут учтены все примыкающие квадраты, после чего формула высказывания считается минимизированной.
Пример: метод карты обычно выполняется путем проверки. Следующий пример расширяет алгебраический метод, чтобы показать «трюк», стоящий за объединением терминов на карте Карно:
- Минтермы № 3 и № 7 упираются, № 7 и № 6 упираются, а № 4 и № 6 упираются (потому что края стола огибают).Таким образом, каждая из этих пар может быть сокращена.
Обратите внимание, что по закону идемпотентности (A ∨ A) = A мы можем создать больше терминов. Тогда по законам ассоциации и распределения исчезающие переменные могут быть объединены в пару, а затем «исчезнут» с Законом противоречия (x & ~ x) = 0. Ниже скобки [и] используются только для отслеживания терминов; они не имеют особого значения:
- Приведите формулу в соединительную нормальную форму с сокращаемой формулой:
- q = ((~ p & d & c) ∨ (p & d & c) ∨ (p & d & ~ c) ∨ (p & ~ d & ~ c)) = ( #3 ∨ #7 ∨ #6 ∨ #4 )
- Идемпотентность (поглощение) [A ∨ A) = A:
- ( #3 ∨ [ #7 ∨ #7 ] ∨ [ #6 ∨ #6 ] ∨ #4 )
- Ассоциативный закон (x ∨ (y ∨ z)) = ((x ∨ y) ∨ z)
- ( [ #3 ∨ #7 ] ∨ [ #7 ∨ #6 ] ∨ [ #6 ∨ #4] )
- [ (~ p & d & c) ∨ (p & d & c) ] ∨ [ (p & d & c) ∨ (p & d & ~ c) ] ∨ [ (p & d & ~ c) ∨ (p & ~ d & ~ c) ].
- Распределительный закон (x & (y ∨ z)) = ((x & y) ∨ (x & z)):
- ([(d & c) ∨ (~ p & p)] ∨ [(p & d) ∨ (~ c & c)] ∨ [(p & ~ c) ∨ (c & ~ c)])
- Коммутативный закон и закон противоречия (x & ~ x) = (~ x & x) = 0:
- ([(d & c) ∨ (0)] ∨ [(p & d) ∨ (0)] ∨ [(p & ~ c) ∨ (0)])
- Закон тождества (x ∨ 0) = x, приводящий к сокращенной форме формулы:
- q = ((d & c) ∨ (p & d) ∨ (p & ~ c))
Проверить редукцию с помощью таблицы истинности
| ряд | Минтермс | п | d | c | ( | ( | d | & | c | ) | ∨ | ( | п | & | d | ) | ∨ | ( | п | & | ~ | ( | c | ) | ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (~ p & ~ d & ~ c) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 1 | (~ p & ~ d & c) | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||||||||
| 2 | (~ p & d & ~ c) | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 3 | (~ p & d & c) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||
| 4 | (p & ~ d & ~ c) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 5 | (p & ~ d & c) | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||||
| 6 | (p & d & ~ c) | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 7 | (p & d & c) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |||||||||
| q |
Неопровержимые предложения
Учитывая следующие примеры-как-определения, что можно сделать с последующими рассуждениями:
- (1) «Это простое предложение». (2) «Это сложное предложение, которое соединяется оператором AND».
Затем присвойте переменную «s» самому левому предложению «Это простое предложение». Определите "составное" c = "not simple" ~ s и присвойте c = ~ s "Это предложение является составным"; присвоить «j» значение «Оно [это предложение] соединено оператором AND». Второе предложение можно выразить так:
- (НЕ (а) И j)
Если значения истинности должны быть помещены в предложения c = ~ s и j, тогда все они явно ЛОЖНЫ: например, «Это сложное предложение» - ЛОЖЬ (это просто, по определению). Так что их союз (И) - ложь. Но в собранном виде предложение - ПРАВДА.
Это пример парадоксы это результат предварительное определение - то есть, когда объект m имеет свойство P, но объект m определен в терминах свойства P.[22] Лучший совет для ритора или специалиста, занимающегося дедуктивным анализом, - избегать непредикативных определений, но в то же время быть начеку, потому что они действительно могут создавать парадоксы. С другой стороны, инженеры заставляют их работать в форме пропозициональных формул с обратной связью.
Формула высказывания с «обратной связью»
Понятие пропозициональной формулы, появляющейся как одна из своих собственных переменных, требует правила формирования, которое позволяет присвоить формулу переменной. В общем, нет никаких условий (как аксиоматические, так и системы таблиц истинности объектов и отношений), которые запрещали бы это происходить.[23]
Самый простой случай возникает, когда формула ИЛИ становится одним из собственных входов, например. р = д. Начнем с (p ∨ s) = q, затем пусть p = q. Заметьте, что «определение» q зависит от самого «q», а также от «s» и связки ИЛИ; это определение q, таким образом, непредсказуемыйРезультатом может быть одно из двух условий:[24] колебание или память.
Это помогает думать о формуле как о черный ящик. Без знания того, что происходит «внутри» формулы- «коробки» снаружи, может показаться, что результат больше не является функция только входов. То есть, иногда кто-то смотрит на q и видит 0, а иногда 1. Чтобы избежать этой проблемы, нужно знать государственный (условие) «скрытой» переменной p внутри поля (т.е. значение q, возвращенное и присвоенное p). Когда это известно, очевидное несоответствие исчезает.
Чтобы понять [предсказать] поведение формул с обратной связью, требуется более сложный анализ последовательные схемы. Формулы высказываний с обратной связью в своей простейшей форме приводят к конечным автоматам; они также приводят к воспоминаниям в виде лент Тьюринга и счетчиков контр-машины. Из комбинаций этих элементов можно построить любую ограниченную вычислительную модель (например, Машины Тьюринга, счетные машины, зарегистрировать машины, Компьютеры Macintosh, так далее.).
Колебание
В абстрактном (идеальном) случае простейшая осциллирующая формула - это НЕ, возвращаемое самому себе: ~ (~ (p = q)) = q. Анализ абстрактной (идеальной) пропозициональной формулы в таблице истинности обнаруживает несоответствие как для случаев p = 1, так и для p = 0: когда p = 1, q = 0, этого не может быть, потому что p = q; то же самое для случаев, когда p = 0 и q = 1.
| q | |||||||
|---|---|---|---|---|---|---|---|
| п | ~ | ( | п | ) | = q | ||
| 0 | 1 | 0 | 1 | вопросы и ответы несовместимы | |||
| 1 | 0 | 1 | 0 | вопросы и ответы несовместимы |

Колебание с задержкой: Если задержка[25] (идеальный или неидеальный) вставляется в абстрактную формулу между p и q, тогда p будет колебаться между 1 и 0: 10 10 10 ... 101 ... до бесконечности. Если задержка и НЕ являются абстрактными (т. Е. Не идеальными), тип анализа, который будет использоваться, будет зависеть от точной природы объектов, составляющих осциллятор; такие вещи выходят за рамки математики и инженерии.
Анализ требует, чтобы была вставлена задержка, а затем разрыв цикла между задержкой и входом «p». Задержку следует рассматривать как своего рода предложение, в котором «qd» (с задержкой q) является выходом, а «q» - входом. Это новое предложение добавляет еще один столбец в таблицу истинности. Несоответствие теперь между «qd» и «p», как показано красным; два стабильных состояния в результате:
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| qd | п | ( | ~ | ( | п | ) | = q | |
| 0 | 0 | 1 | 0 | 1 | состояние 1 | |||
| 0 | 1 | 0 | 1 | 0 | qd & p несовместимы | |||
| 1 | 0 | 1 | 0 | 1 | qd & p несовместимы | |||
| 1 | 1 | 0 | 1 | 0 | состояние 0 |
объем памяти

Без промедления необходимо устранить несоответствия из анализа таблицы истинности. С понятием «задержка» это условие представляет собой мгновенное несоответствие между выходной переменной обратной связи q и p = q.отложенный.
Таблица истинности показывает строки, в которых возникают несоответствия между p = qотложенный на входе и q на выходе. После "нарушения" обратной связи[26] построение таблицы истинности происходит обычным образом. Но после этого в каждой строке вывод q сравнивается с теперь независимым вводом p, и отмечаются любые несоответствия между p и q (т.е. p = 0 вместе с q = 1 или p = 1 и q = 0); когда «линия» «переделана», оба становятся невозможными по Закону противоречия ~ (p & ~ p)). Строки, выявляющие несоответствия, считаются переходные состояния или просто исключены как непоследовательные и, следовательно, «невозможные».
Однажды перевернутая память
О простейших результатах памяти, когда выход ИЛИ возвращается на один из его входов, в этом случае выход «q» возвращается в «p». Учитывая, что формула сначала вычисляется (инициализируется) с p = 0 и q = 0, она «перевернется» один раз, когда «установлена» на s = 1. После этого выход «q» будет поддерживать «q» в «перевернутом» состоянии (состояние q = 1). Это поведение, теперь зависящее от времени, показано диаграмма состояний справа от однократного переворота.
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| п | s | ( | s | ∨ | п | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | состояние 0, s = 0 | ||
| 0 | 1 | 1 | 1 | 0 | вопросы и ответы несовместимы | |||
| 1 | 0 | 0 | 1 | 1 | 1 | состояние 1 с s = 0 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | состояние 1 с s = 1 |
Флип-флоп памяти
Следующий простейший случай - «установка-сброс». резкий поворот показано ниже однократного переворота. Учитывая, что r = 0 & s = 0 и q = 0 в начале, он «устанавливается» (s = 1) аналогично однократному переворачиванию. Однако он имеет возможность «сбросить» q = 0, когда «r» = 1. И дополнительная сложность возникает, если и set = 1, и reset = 1. В этой формуле набор = 1 силы выход q = 1, поэтому когда и если (s = 0 & r = 1) триггер будет сброшен. Или, если (s = 1 & r = 0) будет установлен триггер. В абстрактном (идеальном) примере, в котором одновременно s = 1 ⇒ s = 0 & r = 1 ⇒ r = 0, формула q будет неопределенной (неразрешимой). Из-за задержек в "реальном" ИЛИ, И и НЕ результат будет неизвестен вначале, но впоследствии предсказуем.
| q | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| п | s | р | ( | s | ∨ | ( | п | & | ~ | ( | р | ) | ) | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | состояние 0 с (s = 0 & r = 0) | ||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | состояние 0 с (s = 0 & r = 1) | ||||||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | вопросы и ответы несовместимы | |||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | вопросы и ответы несовместимы | |||||||
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | состояние 1 с (s = 0 & r = 0) | ||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | вопросы и ответы несовместимы | |||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | состояние 1 с (s = 1 & r = 0) | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | состояние 1 с s & r одновременно 1 |
Память с синхронизацией триггера
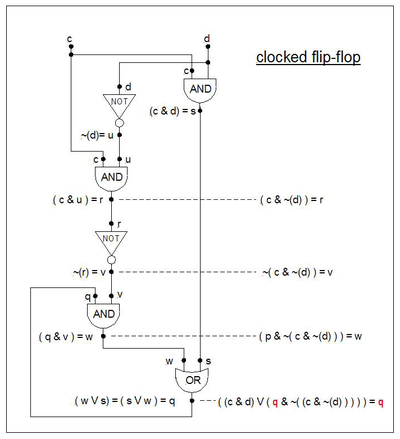
Формула, известная как «синхронизированная триггерная память» («c» - это «часы», а «d» - «данные»), приведена ниже. Это работает следующим образом: когда c = 0, данные d (0 или 1) не могут «пройти», чтобы повлиять на выход q. Когда c = 1, данные d «проходят», а выход q «следует» за значением d. Когда c изменяется от 1 до 0, последнее значение данных остается "захваченным" на выходе "q". Пока c = 0, d может изменять значение, не вызывая изменения q.
- Примеры
- ((c & d) ∨ ( п & (~ (c & ~ (d)))) = q, но теперь пусть p = q:
- ((c & d) ∨ ( q & (~ (c & ~ (d)))) = q
Диаграмма состояний похожа по форме на диаграмму состояний триггера, но с другой маркировкой на переходы.
| s | q | ш | v | р | ты | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ряд | q | d | c | ( | ( | c | & | d | ) | ∨ | ( | q | & | ~ | ( | ( | c | & | ~ | ( | d | ) | ) | ) | ) | ) | = q | Описание |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | состояние 0 с (s = 0 & r = 0), 0 захвачен | ||||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | состояние 0 с (d = 0 & c = 1): q = 0 следует за d = 0 | ||||||||||||
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | состояние 0 с (d = 1 & r = 0), 0 захвачен | ||||||||||||
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | вопросы и ответы несовместимы | |||||||||||||
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | состояние 1 с (d = 0 & c = 0), 1 захвачен | ||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | вопросы и ответы несовместимы | |||||||||||||
| 6 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | состояние 1 с (d = 1 & c = 0), 1 захвачен | ||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | состояние 1 с (d = 1 & c = 1): q = 1 следует за d = 1 |
Историческое развитие
Бертран Рассел (1912: 74) перечисляет три закона мысли, которые происходят из Аристотель: (1) закон личности: «Все, что есть, есть», (2) закон непротиворечивости: «Ничто не может быть и не быть», и (3) закон исключенного среднего: «Все должно быть или не быть».
- Пример: Здесь O - это выражение о БЫТИИ или КАЧЕСТВЕ объекта:
- Закон идентичности: O = O
- Закон противоречия: ~ (O & ~ (O))
- Закон исключенной середины: (O ∨ ~ (O))
Использование слова «все» в законе исключенного третьего делает выражение этого закона Расселом открытым для обсуждения. Если ограничиться выражением о БЫТИИ или КАЧЕСТВЕ применительно к конечному набору объектов (конечной «вселенной дискурса»), члены которой можно исследовать один за другим на предмет наличия или отсутствия утверждения, - тогда закон считается интуитивно подходящим. Таким образом, утверждение типа: «Этот объект должен БЫТЬ или НЕ БЫТЬ (в коллекции)» или «Этот объект должен иметь это КАЧЕСТВО или НЕ иметь это КАЧЕСТВО (относительно объектов в коллекции)» является приемлемым. Смотрите больше на Диаграмма Венна.
Хотя исчисление высказываний возникло у Аристотеля, понятие алгебра применительно к предложениям пришлось подождать до начала 19 века. В (неблагоприятной) реакции на 2000-летнюю традицию Аристотеля силлогизмы, Джон Локк с Очерк человеческого понимания (1690) использовал слово семиотика (теория употребления символов). К 1826 г. Ричард Уэйтли критически проанализировал силлогистическую логику с симпатией к семиотике Локка. Джордж Бентам Работа (1827 г.) привела к появлению понятия «количественная оценка предиката» (1827 г.) (в настоящее время обозначается как ∀ ≡ «для всех»). "Ссора", спровоцированная Уильям Гамильтон по приоритетному спору с Огастес Де Морган "вдохновленный Джордж Буль написать свои идеи по логике и опубликовать их как MAL [Математический анализ логики] в 1847 г. »(Grattin-Guinness and Bornet 1997: xxviii).
О своем вкладе комментируют Граттин-Гиннесс и Борнет:
- "Основным нововведением Буля был [] закон [xп = x] для логики: в нем говорится, что мысленные действия по выбору свойства x и повторному выбору x аналогичны выбору x один раз ... В результате он сформировал уравнения x • (1-x) = 0 и x + (1-x) = 1, что для него выражало, соответственно, закон противоречия и закон исключенного среднего »(стр. xxviiff). Для логического« 1 »было вселенная дискурса а «0» ничего не значило.
Готтлоб Фреге Массовое предприятие (1879 г.) привело к формальному исчислению предложений, но его символика настолько устрашающа, что оказала небольшое влияние, за исключением одного человека: Бертран Рассел. Сначала как студент Альфред Норт Уайтхед он изучил работу Фреге и предложил (известную и печально известную) поправку к ней (1904 г.) вокруг проблемы антиномия что он обнаружил в трактовке Фреге (ср. Парадокс Рассела ). Работа Рассела привела к сотрудничеству с Уайтхедом, который в 1912 году выпустил первый том Principia Mathematica (ВЕЧЕРА). Именно здесь впервые появилась то, что мы считаем «современной» логикой высказываний. В частности, PM вводит НЕ и ИЛИ, а также символ утверждения ⊦ как примитивы. В терминах этих понятий они определяют ИМПЛИКАЦИЯ → (по умолчанию * 1.01: ~ p ∨ q), затем И (по умолчанию * 3.01: ~ (~ p ∨ ~ q)), затем ЭКВИВАЛЕНТНОСТЬ p ← → q (* 4.01: ( p → q) & (q → p)).
- Генри М. Шеффер (1921) и Жан Никод демонстрируют, что только одна связка, «штрих» | достаточно, чтобы выразить все пропозициональные формулы.
- Эмиль Пост (1921) развивает метод анализа таблицы истинности в своем «Введении в общую теорию элементарных предложений». Он отмечает инсульт Никода | .
- Уайтхед и Рассел добавляют введение к своему переизданию ПМ в 1927 году, частично добавляя благоприятное отношение к «инсульту».
Вычислительная и коммутационная логика:
- Уильям Экклс и Ф. В. Джордан (1919) описывают «пусковое реле», сделанное из вакуумной лампы.
- Джордж Стибиц (1937) изобретает двоичный сумматор с использованием механических реле. Он строит это на своем кухонном столе.
- Пример: данный двоичный биты ая и бя и ручная кладь (c_inя), их сумма Σя и выполнить (c_outя) находятся:
- ((ая XOR bя ) XOR c_inя ) = Σя
- (ая & bя ) ∨ c_inя ) = c_outя;
- Алан Тьюринг строит умножитель, используя реле (1937–1938). Для этого ему нужно вручную намотать катушки реле.
- Учебники по «коммутационным схемам» появляются в начале 1950-х годов.
- Уиллард Куайн 1952 и 1955 гг., Э. В. Вейч 1952 г. и М. Карно (1953) разработали методы отображения для упрощения пропозициональных функций.
- Джордж Х. Мили (1955) и Эдвард Ф. Мур (1956) обращаются к теории последовательных (т. Е. С коммутационной схемой) «машин».
- Э. Дж. Маккласки и Х. Шорр разработали метод упрощения пропозициональных (коммутационных) схем (1962).
Сноски
- ^ Гамильтон 1978: 1
- ^ Principia Mathematica (PM) стр. 91 избегает «того», потому что им нужен четкий «объект ощущения»; они предусматривают использование слова «это»
- ^ (курсив добавлен) Райхенбах[требуется разъяснение ] стр.80.
- ^ Тарский с.54-68. Суппес называет ИДЕНТИЧНОСТЬ «дополнительным правилом вывода» и вкратце разворачивает его; Роббин, Бендер, Уильямсон и Гудштейн представляют знак и его использование без комментариев и объяснений. Гамильтон П. 37 использует два знака ≠ и = по отношению к оценка формулы в формальном исчислении. Kleene p. 70 и Гамильтон стр. 52 поместите его в исчисление предикатов, в частности, в отношении арифметики натуральных чисел.
- ^ Эмпирики избегают понятия априори (встроенные, рожденные с) знания. «Радикальные редукционисты», такие как Джон Локк и Дэвид Хьюм «считал, что каждая идея должна либо возникать непосредственно из чувственного опыта, либо быть составной из идей, возникающих таким образом»; цитата из Куайна, переизданного в 1996 г. Возникновение логического эмприризма, Garland Publishing Inc. http://www.marxists.org/reference/subject/philosophy/works/us/quine.htm
- ^ Нейронная сеть моделирование предлагает хорошую математическую модель для компаратора следующим образом: для сигнала S и порогового значения "th" вычтите "th" из S и замените эту разницу d на a сигмовидная функция: Для больших "выигрышей" k, например k = 100, 1 / (1 + e−k * d ) = 1 / (1 + e−k * (S-th) ) = { ≃0, ≃1 }.[требуется разъяснение ] Например, если «Дверь ВНИЗ» означает «Дверь находится менее чем на 50% пути вверх», то пороговое значение th = 0,5, соответствующее 0,5 * 5,0 = +2,50 вольт, может быть применено к «линейному» измерению - устройство с выходом 0 вольт при полностью закрытом состоянии и +5,0 вольт при полностью открытом состоянии.
- ^ На самом деле цифровые 1 и 0 определены в неперекрывающихся диапазонах, например. {"1" = + 5 / + 0,2 / -1,0 вольт, 0 = + 0,5 / -0,2 вольт}[требуется разъяснение ]. Когда значение выходит за пределы определенного диапазона (ов), значение становится «u» - неизвестно; например +2,3 будет "u".
- ^ Хотя понятие логического произведения не так уж необычно (например, 0 * 0 = 0, 0 * 1 = 0, 1 * 0 = 0, 1 * 1 = 1), понятие (1 + 1 = 1 является своеобразный; фактически (a "+" b) = (a + (b - a * b)), где "+" - это "логическая сумма", а + и - истинные арифметические эквиваленты. Иногда все четыре понятия встречаются в формуле: A AND B = 1/2 * (A плюс B минус (A XOR B)] (см. Стр. 146 в John Wakerly 1978, Коды обнаружения ошибок, самопроверяющиеся схемы и приложения, Северная Голландия, Нью-Йорк, ISBN 0-444-00259-6 пбк.)
- ^ Внимательный взгляд на карту Карно показывает, что IF ... THEN ... ELSE также может быть выражено довольно окольным образом в терминах двух исключающих ИЛИ: ((b AND (c XOR a)) OR (а И (с ИСКЛЮЧАЮЩЕЕ ИЛИ b))) = d.
- ^ Роббин П. 3.
- ^ Розенблум с. 30 и стр. 54 и далее подробно обсуждает эту проблему импликации. Большинство философов и математиков просто принимают определение материала, данное выше. Но некоторые этого не делают, в том числе интуиционисты; они считают это неправильной формой закона исключенного третьего.
- ^ Действительно, исчерпывающий выбор между альтернативами - взаимное исключение - требуется по определению, которое Клини дает оператор CASE (Kleene 1952229)
- ^ Использование кавычек вокруг выражений не случайно. Тарский комментирует использование кавычек в его «18. Идентичность вещей и идентичность их обозначений; использование кавычек» с. 58ff.
- ^ Гамильтон П. 37. Бендер и Уильямсон стр. 29 заявите: «В дальнейшем мы заменим« равно »символом« ⇔ »(эквивалентность), который обычно используется в логике. Мы используем более знакомый« = »для присвоения значения и значений».
- ^ Райхенбах п. 20-22 и следует правилам PM. Символ =Df находится в метаязык и не является формальным символом со следующим значением: «символ 's' должен иметь то же значение, что и формула '(c & d)'».
- ^ Розенблум 1950: 32. Kleene 1952: 73-74 ранжирует все 11 символов.
- ^ см. Минский 1967: 75, раздел 4.2.3 «Метод подсчета скобок». Мински представляет конечный автомат, который будет выполнять эту работу, и, используя индукцию (рекурсивное определение), Мински доказывает «метод» и представляет теорему в качестве результата. Полностью обобщенная «грамматика скобок» требует наличия бесконечного конечного автомата (например, машины Тьюринга) для выполнения подсчета.
- ^ Роббин П. 7
- ^ cf Reichenbach p. 68 для более активного обсуждения: «Если вывод верен и посылки верны, вывод называется убедительный.
- ^ Наряду с первыми тремя, Гамильтон стр.19-22 обсуждает логику, построенную только из | (И-НЕ) и ↓ (ИЛИ).
- ^ Wickes 1967: 36 и далее. Wickes предлагает хороший пример 8 карт 2 x 4 (карты с 3 переменными) и 16 карт 4 x 4 (карты с 4 переменными). Поскольку произвольная карта с тремя переменными может представлять любую из двух8= 256 карт 2x4, а произвольная карта с 4 переменными может представлять любую из 216 = 65 536 различных формул-вычислений, записать каждую невозможно.
- ^ Это определение дается Стивен Клини. Обе Курт Гёдель и Клини считал, что классические парадоксы всегда являются примерами такого рода определений. Но Клини продолжал утверждать, что проблема не была решена удовлетворительным образом, и что косвенные определения можно найти в анализ. Он приводит в качестве примера определение наименьшая верхняя граница (l.u.b) ты из M. Учитывая Дедекинда вырезать числовой линии C и две части, на которые разрезана числовая линия, т.е. M и (C - M), l.u.b. знак равно ты определяется в терминах понятия M, в то время как M определяется в терминах C. Таким образом, определение ты, элемент C, определяется в терминах совокупности C и это делает его определение непредсказуемым. Клини утверждает, что попытки оспорить это можно использовать для поддержки непредсказуемых определений парадоксов (Kleene 1952: 43).
- ^ Маккласки комментирует, что «можно утверждать, что анализ еще не завершен, потому что не было получено словосочетание« Выходы равны предыдущим значениям входов »; он продолжает отбрасывать такие опасения, потому что «английский не является формальным языком в математическом смысле, [и] на самом деле невозможно иметь формальный порядок получения словесных утверждений »(с. 185).
- ^ Точнее, при достаточном «усилении контура» либо колебание или же объем памяти произойдет (см. Маккласки, стр. 191-2). В абстрактных (идеализированных) математических системах адекватное усиление контура не является проблемой.
- ^ Понятие задержки и принцип локальной причинности, вызванной, в конечном счете, скоростью света, появляются в Робин Ганди (1980), «Тезис Черча и принципы механизмов», в Дж. Барвайз, Х. Дж. Кейслер и К. Кунен, ред., Клини симпозиум, North-Holland Publishing Company (1980) 123-148. Ганди считал это важнейшим из своих принципов: «Современная физика отвергает возможность мгновенного действия на расстоянии» (стр. 135). Ганди был Алан Тьюринг ученица и близкий друг.
- ^ МакКласки стр. 194-5 обсуждает «разрыв петли» и вставляет для этого «усилители»; Wickes (стр. 118-121) обсуждает вставку задержек. Маккласки стр. 195ff обсуждает проблему «гонок», вызванных задержками.
Рекомендации
- Бендер, Эдвард А. и Уильямсон, С. Гилл, 2005, Краткий курс дискретной математики, Dover Publications, Mineola NY, ISBN 0-486-43946-1. Этот текст используется в «двухквартальном курсе по информатике» в Калифорнийском университете в Сан-Диего.
- Эндертон, Х., 2002, Математическое введение в логику. Harcourt / Academic Press. ISBN 0-12-238452-0
- Гудштейн, Р. Л., (Pergamon Press 1963), 1966, (Dover издание 2007), Булева алгебра, Dover Publications, Inc. Минола, Нью-Йорк, ISBN 0-486-45894-6. Акцент на понятие «алгебра классов» с теоретико-множественными символами, такими как, ∪, '(НЕ), ⊂ (СЛЕДУЕТ). Позже Гольдштейн заменяет их на &, ∨, ¬, → (соответственно) в своей трактовке «Логики предложений», стр. 76–93.
- Айвор Граттан-Гиннесс и Жерар Борне 1997, Джордж Буль: Избранные рукописи по логике и ее философии, Birkhäuser Verlag, Василий, ISBN 978-0-8176-5456-6 (Бостон).
- А. Г. Гамильтон 1978, Логика для математиков, Издательство Кембриджского университета, Кембридж, Великобритания, ISBN 0-521-21838-1.
- Э. Дж. Маккласки 1965, Введение в теорию коммутационных схем, McGraw-Hill Book Company, Нью-Йорк. Нет ISBN. Номер карточки каталога Библиотеки Конгресса 65-17394. Маккласки был учеником Уиллард Куайн и разработал некоторые известные теоремы вместе с Куайном и самостоятельно. Для тех, кто интересуется историей, книга содержит множество ссылок.
- Марвин Л. Мински 1967, Вычисления: конечные и бесконечные машины, Prentice-Hall, Inc, Энглвуд Клиффс, Нью-Джерси. Нет ISBN. Номер карточки Каталога Библиотеки Конгресса 67-12342. Полезно, особенно с точки зрения вычислимости, плюс хорошие источники.
- Пол С. Розенблум 1950 г., Дуврское издание 2005 г., Элементы математической логики, Dover Publications, Inc., Минеола, Нью-Йорк, ISBN 0-486-44617-4.
- Джоэл В. Роббин 1969, 1997, Математическая логика: первый курс, Dover Publications, Inc., Минеола, Нью-Йорк, ISBN 0-486-45018-X (пбк.).
- Патрик Суппес 1957 г. (Дуврское издание 1999 г.), Введение в логику, Dover Publications, Inc., Минеола, Нью-Йорк. ISBN 0-486-40687-3 (пбк.). Эта книга уже напечатана и легко доступна.
- На своей странице 204 в сноске он ссылается на свой набор аксиом на Э. В. Хантингтон, "Наборы независимых постулатов для алгебры логики", Труды Американского математического общества, Vol. 5 91904), с. 288-309.
- Альфред Тарский 1941 (Дуврское издание 1995 г.), Введение в логику и методологию дедуктивных наук, Dover Publications, Inc., Минеола, Нью-Йорк. ISBN 0-486-28462-X (пбк.). Эта книга уже напечатана и легко доступна.
- Жан ван Хейеноорт 1967 г., 3-е издание с изменениями 1976 г., От Фреге до Гёделя: Справочник по математической логике, 1879-1931 гг., Издательство Гарвардского университета, Кембридж, Массачусетс. ISBN 0-674-32449-8 (pbk.) Перевод / оттиски Фреге (1879), письма Рассела Фреге (1902) и письма Фреге Расселу (1902), парадокса Ричарда (1905), Поста (1921) можно найти здесь.
- Альфред Норт Уайтхед и Бертран Рассел 1927 г. 2-е издание, издание в мягкой обложке до * 53 1962 г., Principia Mathematica, Cambridge University Press, без ISBN. В период между первым изданием 1912 года и вторым изданием 1927 года Х.М. Шеффер 1921 и М. Жан Никод (год не указан) обратил внимание Рассела и Уайтхеда на то, что то, что они считали своими примитивными предложениями (связками), можно свести к единственному |, ныне известному как «штрих» или И-НЕ (НЕ-И, НИ НИ ... НИ .. .).Рассел-Уайтхед обсуждает это в своем «Введении ко второму изданию» и дает определения, как обсуждалось выше.
- Уильям Э. Уикс 1968, Логический дизайн с интегральными схемами, John Wiley & Sons, Inc., Нью-Йорк. Нет ISBN. Номер карточки каталога Библиотеки Конгресса: 68-21185. Подробное изложение инженерных методов анализа и синтеза, ссылается на McCluskey 1965. В отличие от Суппеса, представление Уикса «булевой алгебры» начинается с набора постулатов, имеющего характер таблицы истинности, а затем выводит из них обычные теоремы (стр. 18ff).
внешняя ссылка
 СМИ, связанные с Пропозициональная формула в Wikimedia Commons
СМИ, связанные с Пропозициональная формула в Wikimedia Commons


























