Шестерни - Gear



А передача это вращающийся круговой машина деталь со срезанными зубьями или, в случае зубчатое колесо или шестерня, вставленные зубы (называемые винтики), которые сцепляются с другой зубчатой частью для передачи крутящий момент. Шестеренка может также неофициально называться винтик. Редукторные устройства могут изменять скорость, крутящий момент и направление движения источник питания. Шестерни разных размеров изменяют крутящий момент, создавая механическое преимущество через их передаточное число, и поэтому может считаться простая машина. В скорость вращения, а крутящие моменты двух зацепляющих шестерен различаются пропорционально их диаметрам. Зубья на двух зубчатых колесах имеют одинаковую форму.[1]
Две или более зубчатых передачи, работающих последовательно, называются зубчатая передача или коробка передач. Шестерни в трансмиссии аналогичны колесам перекрестного ремня. шкив система. Преимущество шестерен в том, что зубья шестерни предотвращают проскальзывание. В трансмиссиях с несколькими передаточными числами, таких как велосипеды, мотоциклы и автомобили, термин «передача» (например, «первая передача») относится к передаточному отношению, а не к реальной физической передаче. Этот термин описывает аналогичные устройства, даже если передаточное число является непрерывным, а не дискретным, или когда устройство фактически не содержит шестерен, как в бесступенчатая трансмиссия.[2]
Кроме того, шестерня может зацепляться с линейной зубчатой частью, называемой стойка, производя перевод вместо вращения.
История
Ранние образцы шестерен датируются 4 веком до нашей эры в Китае.[3] (Времена Чжань Го - Поздний Восток Династия Чжоу ), сохранившиеся в Лоянский музей провинции Хэнань, Китай. Самые ранние сохранившиеся шестерни в Европе были найдены в Антикитерский механизм, пример очень раннего и сложного устройства, предназначенного для расчета астрономический позиции. Время его постройки сейчас оценивается между 150 и 100 годами до нашей эры.[4] Шестерни появляются в работах, связанных с Герой Александрии, в Римский Египет около 50 г.[5] но его можно проследить до механики Александрийская школа в 3 веке до нашей эры Птолемеевский Египет, и были сильно развиты греческими эрудит Архимед (287–212 гг. До н.э.).[6]

Сегментарная передача, которая принимает / передает возвратно-поступательное движение от / к зубчатому колесу, состоящему из сектора круговой шестерни / кольца с зубьями на периферии,[7] был изобретен арабским инженером Аль-Джазари в 1206 г.[8] В червячный редуктор был изобретен в Индийский субконтинент, для использования в роликах хлопкоочистительные машины, где-то в XIII – XIV вв.[9] Дифференциальный шестерни, возможно, использовались в некоторых китайских указывающие на юг колесницы,[10] но первое поддающееся проверке использование дифференциальных передач было сделано британским часовщиком Джозефом Уильямсоном в 1720 году.
Примеры применения раннего снаряжения:
- 1386 г. н.э. Часы Солсберийского собора: это самые старые в мире все еще работающие механические часы с редуктором.
- c. 13–14 вв.: червячный редуктор был изобретен как часть ролика хлопкоочистительный в Индийский субконтинент.[9]
- c. 1221 г. н.э. астролябия был построен в Исфахан показывая положение Луна в зодиак и это фаза, и количество дней после новолуния.[11]
- c. 1206 г. н.э .:Аль-Джазари изобрел сегментный механизм как часть водоподъемного устройства.[8]
- 725 г. н.э .: первые механические часы были построены в Китай.
- c. 200–265 гг. Н. Э .: Ма Цзюнь использовали шестерни как часть колесница, указывающая на юг.
- 2 век до нашей эры: Антикитерский механизм
- В природе: в задних лапах нимф кузнечика. Иссус колеоптратус.
Этимология
Слово передача вероятно из Древнескандинавский Горви (множественное число Gørvar) "одежда, снаряжение", относящиеся к Гёра, Горва 'делать, строить, строить; установить порядок, подготовить, 'глагол, распространенный в древнескандинавском языке, «используется в широком диапазоне ситуаций, от написания книги до заправки мяса». В этом контексте значение слова «зубчатое колесо в машинах» впервые засвидетельствовано 1520-ми годами; особый механический смысл «частей, с помощью которых двигатель сообщает движение» - с 1814 г .; конкретно транспортного средства (велосипеда, автомобиля и т. д.) к 1888 году.[12]


А винтик зуб на колесе. От Средний английский зубчатый, от Древнескандинавский (сравнить Норвежский Кугг ('винтик'), Шведский Кугг, Кугге ('зубец, зуб')), от Прото-германский *Кугго (сравнить Голландский Kogge ('шестеренка '), Немецкий Kock), от Протоиндоевропейский *гуга ('горб, мяч') (сравнить Литовский гуга ('лука, горб, холм'), от ПИРОГ *gēw- ('гнуть, выгибать').[13] Впервые использовал c. 1300 в смысле «колесо с зубьями или зубьями»; конец 14 в., «зуб на колесе»; зубчатое колесо, начало 15 века.[14]
Исторически зубья были сделаны из дерева, а не из металла, а зубчатое колесо технически состояло из ряда деревянных зубцов шестерни, расположенных вокруг врезного колеса, причем каждый зуб образовывал особый тип. 'сквозной' паз и шип совместный. Колесо может быть деревянным, чугун, или другой материал. Деревянные зубья раньше использовались, когда нельзя было разрезать большие металлические шестерни, когда литой зуб не имел даже приблизительно правильной формы или когда размер колеса делал производство непрактичным.[15]
Винтики часто делались из клен дерево. В 1967 году производственная компания Томпсона Ланкастер, Нью-Гэмпшир все еще вел активный бизнес по поставке десятков тысяч зубьев клиновой шестерни в год, в основном для использования в бумажная фабрика и зерновые мельницы, некоторым из которых более 100 лет.[16] Поскольку деревянный зубец выполняет точно такую же функцию, что и литой или обработанный металлический зуб, это слово было применено как расширение к обоим, и различие в целом было потеряно.
Сравнение с приводными механизмами
Определенное передаточное отношение, которое зубья дают шестерням, дает преимущество перед другими приводами (такими как тяга диски и Клиновые ремни ) в точных машинах, таких как часы, которые зависят от точного отношения скоростей. В случаях, когда привод и ведомый элемент расположены близко друг к другу, шестерни также имеют преимущество перед другими приводами в меньшем количестве требуемых деталей. Обратной стороной является то, что шестерни дороже в производстве, а требования к смазке могут повлечь более высокие эксплуатационные расходы в час.
Типы
Внешние и внутренние шестерни

An внешняя передача представляет собой зубцы, образованные на внешней поверхности цилиндра или конуса. И наоборот, внутренняя передача представляет собой зубцы, сформированные на внутренней поверхности цилиндра или конуса. Для конические шестерни, внутренняя шестерня - это одно с подача угол более 90 градусов. Внутренние шестерни не вызывают изменения направления выходного вала.[17]
Шпора
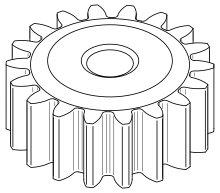
Прямозубые шестерни или прямозубые шестерни являются простейшими типами снастей. Они состоят из цилиндра или диска с радиально выступающими зубьями. Хотя зубья не прямые (но обычно имеют особую форму для достижения постоянного передаточного числа, в основном эвольвента но реже циклоидальный ) край каждого зуба прямой и выровнен параллельно оси вращения. Эти шестерни правильно зацепляются друг с другом только в том случае, если они установлены на параллельных валах.[18] Нагрузки на зубья не создают осевой тяги. Прямозубые шестерни превосходны на средних скоростях, но имеют тенденцию к шуму на высоких скоростях.[19]
Спиральный


Вверху: параллельная конфигурация
Внизу: перекрестная конфигурация
Спиральный или «сухие фиксированные» зубчатые колеса предлагают усовершенствование по сравнению с цилиндрическими зубчатыми колесами. Передние кромки зубьев не параллельны оси вращения, а расположены под углом. Поскольку шестерня изогнута, этот наклон делает зуб в форме сегмента спираль. Цилиндрические шестерни могут входить в зацепление параллельно или скрещенный ориентации. Первое относится к случаям, когда валы параллельны друг другу; это наиболее распространенная ориентация. В последнем случае валы не параллельны, и в этой конфигурации шестерни иногда называют «косыми шестернями».
Угловые зубья входят в зацепление более плавно, чем зубья прямозубой шестерни, благодаря чему они работают более плавно и тихо.[20] В параллельных косозубых зубчатых колесах каждая пара зубьев сначала входит в контакт в одной точке на одной стороне зубчатого колеса; затем движущаяся кривая контакта постепенно нарастает по поверхности зуба до максимума, затем отступает, пока зубцы не прервут контакт в одной точке на противоположной стороне. В цилиндрических зубчатых колесах зубья внезапно встречаются в прямом контакте по всей своей ширине, вызывая напряжение и шум. Прямозубые шестерни издают характерный вой на высоких оборотах. По этой причине прямозубые цилиндрические шестерни используются в низкоскоростных приложениях и в ситуациях, когда снижение шума не является проблемой, а косозубые шестерни используются в высокоскоростных приложениях, при передаче большой мощности или там, где снижение шума это важно.[21] Скорость считается высокой, если скорость продольной оси превышает 25 м / с.[22]
Недостатком косозубых шестерен является толчок вдоль оси шестерни, которая должна быть размещена соответствующими упорные подшипники. Однако эту проблему можно превратить в преимущество при использовании шестеренка в елочку или двойная косозубая шестерня, который не имеет осевой тяги - а также обеспечивает самовыравнивание шестерен. Это приводит к меньшей осевой нагрузке, чем у сопоставимой цилиндрической зубчатой передачи.
Второй недостаток косозубых шестерен - это также большая степень трение скольжения между зубьями зацепления, часто обращаются с присадками в смазке.
Косые шестерни
Для «скрещенной» или «косой» конфигурации шестерни должны иметь одинаковый угол сжатия и нормальный шаг; однако угол наклона спирали и рукоятка могут быть разными. Взаимосвязь между двумя валами фактически определяется углом (углами) спирали двух валов и вращением, как определено:[23]
- для шестерен одинаковой руки,
- для шестерен разнонаправленных,
где угол винтовой линии зубчатой передачи. Скрещенная конфигурация менее механически надежна, потому что между шестернями имеется только точечный контакт, тогда как в параллельной конфигурации есть линейный контакт.[23]
Довольно часто используются косозубые шестерни с углом наклона винтовой линии одной винтовой линии, отрицательным по отношению к углу винтовой линии другой; такую пару можно также назвать имеющей правую спираль и левую спираль с равными углами. Два равных, но противоположных угла складываются в ноль: угол между валами равен нулю, то есть валы параллельно. Если сумма или разность (как описано в уравнениях выше) не равна нулю, валы скрещенный. Для валов скрещенный под прямыми углами углы спирали имеют одинаковое значение, потому что они должны составлять 90 градусов. (Так обстоит дело с шестернями на иллюстрации выше: они правильно зацепляются в перекрещенной конфигурации: для параллельной конфигурации один из углов винтовой линии должен быть изменен на противоположное. Изображенные шестерни не могут зацепляться с параллельными валами.)
Двойная спираль

Двойные косозубые шестерни преодолевают проблему осевого усилия, создаваемого одинарными косозубыми шестернями, за счет использования двойного набора зубцов, наклоненных в противоположных направлениях. Двойную косозубую шестерню можно рассматривать как две зеркальные косозубые шестерни, установленные близко друг к другу на общей оси. Эта конструкция нейтрализует чистую осевую нагрузку, поскольку каждая половина шестерни толкает в противоположном направлении, в результате чего результирующая осевая сила равна нулю. Такое расположение также может устранить необходимость в упорных подшипниках. Однако двойные косозубые шестерни сложнее изготовить из-за их более сложной формы.
Шестерни в елочку представляют собой особый вид косозубых шестерен. У них нет паза посередине, как у некоторых других двойных косозубых шестерен; две зеркальные косозубые шестерни соединены вместе так, что их зубья образуют V-образную форму. Это также можно применить к конические шестерни, как в главная передача из Citroën Тип А.
Для обоих возможных направлений вращения существуют два возможных варианта расположения противоположно ориентированных косозубых шестерен или поверхностей шестерен. Одно устройство называется стабильным, а другое - нестабильным. В устойчивом расположении поверхности косозубой шестерни ориентированы так, что каждая осевая сила направлена к центру шестерни. В нестабильной конструкции обе осевые силы направлены от центра шестерни. В любом случае общая (или сеть) осевое усилие на каждой шестерне равно нулю, если шестерни правильно выровнены. Если шестерни смещаются в осевом направлении, неустойчивое устройство создает результирующую силу, которая может привести к разборке зубчатой передачи, в то время как стабильная конструкция создает чистую корректирующую силу. Если направление вращения меняется на противоположное, направление осевых усилий также меняется на противоположное, поэтому стабильная конфигурация становится нестабильной, и наоборот.
Стабильные двойные косозубые шестерни можно напрямую заменять прямозубыми цилиндрическими шестернями без необходимости установки других подшипников.
Скос


Коническая шестерня имеет форму правильный круговой конус с обрезанной большей частью кончика. Когда две конические шестерни входят в зацепление, их воображаемые вершины должны находиться в одной точке. Оси их валов также пересекаются в этой точке, образуя произвольный непрямой угол между валами. Угол между валами может быть любым, кроме нуля или 180 градусов. Конические шестерни с равным количеством зубьев и осями вала под углом 90 градусов называются косыми (США) или косыми (Великобритания) шестернями.
Спиральные фаски

Спирально-конические зубчатые колеса могут быть изготовлены как типы Gleason (дуга окружности с непостоянной глубиной зуба), типы Oerlikon и Curvex (дуга окружности с постоянной глубиной зуба), Klingelnberg Cyclo-Palloid (эпициклоида с постоянной глубиной зуба) или Klingelnberg Palloid. Спирально-конические зубчатые колеса имеют те же преимущества и недостатки по сравнению со своими собратьями с прямым нарезанием, что и косозубые зубчатые колеса с цилиндрическими зубчатыми колесами. Прямые конические передачи обычно используются только на скоростях ниже 5 м / с (1000 футов / мин) или, для малых передач, 1000 об / мин.[24]
Примечание: профиль зуба цилиндрической шестерни соответствует эвольвенте, а профиль зуба конической шестерни - восьмигранной. Все традиционные генераторы конических зубчатых колес (такие как Gleason, Klingelnberg, Heidenreich & Harbeck, WMW Modul) производят конические шестерни с восьмигранным профилем зуба. : Для 5-осевых фрезерованных конических зубчатых колес важно выбрать тот же расчет / компоновку, что и при обычном методе производства. Упрощенные расчетные конические зубчатые колеса на основе эквивалентной цилиндрической зубчатой передачи в нормальном сечении с эвольвентной формой зуба демонстрируют отклоняющуюся форму зуба с уменьшением прочности зуба на 10-28% без смещения и на 45% со смещением [Дисс. Hünecke, TU Dresden]. Кроме того, «эвольвентные конические зубчатые колеса» вызывают больше шума.
Гипоидный
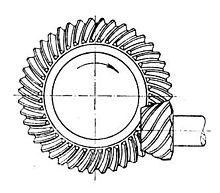
Гипоидные шестерни напоминают спирально-конические шестерни, за исключением того, что оси валов не пересекаются. Поверхности деления кажутся коническими, но, чтобы компенсировать смещение вала, на самом деле гиперболоиды революции.[25][26] Гипоидные шестерни почти всегда рассчитаны на работу с валами под углом 90 градусов. В зависимости от того, с какой стороны смещен вал относительно наклона зубьев, контакт между зубьями гипоидной шестерни может быть даже более плавным и постепенным, чем с зубьями спирально-конической шестерни, но также иметь скользящее действие вдоль зубьев зацепления при вращении. и поэтому обычно требуются некоторые из наиболее вязких типов трансмиссионного масла, чтобы избежать его вытеснения с поверхностей сопрягаемых зубьев, масло обычно обозначается HP (для гипоида), за которым следует число, обозначающее вязкость. Так же шестерня может быть сконструирован с меньшим количеством зубьев, чем спиральная коническая шестерня, в результате чего передаточное число 60: 1 и выше становится возможным при использовании одного набора гипоидных шестерен.[27] Этот тип шестерни наиболее распространен в трансмиссии автомобилей, в сочетании с дифференциал. В то время как обычный (негипоидный) зубчатый венец и шестерня подходит для многих применений, он не идеален для трансмиссии транспортных средств, поскольку создает больше шума и вибрации, чем гипоидный. Вывод на рынок гипоидных шестерен для массового производства был инженерным усовершенствованием 1920-х годов.
Корона

Корона шестерни или сокращать передачи представляют собой коническую шестерню особой формы, зубья которой выступают под прямым углом к плоскости колеса; по своей ориентации зубы напоминают острие на коронке. Коронная шестерня может точно зацепляться только с другой конической шестерней, хотя коронная шестерня иногда зацепляется с прямозубыми шестернями. Коронная шестерня также иногда зацепляется с спусковой механизм например, в механических часах.
Червь


черви походить винты. Червь связан с червячное колесо, который похож на цилиндрическое прямозубое колесо.
Червячные передачи - это простой и компактный способ достижения высокого крутящего момента и низкого передаточного числа. Например, косозубые шестерни обычно ограничиваются передаточным числом менее 10: 1, в то время как червячные передачи варьируются от 10: 1 до 500: 1.[28] Недостатком является возможность значительного скольжения, что приводит к низкой эффективности.[29]
Червячная шестерня - это разновидность косозубой шестерни, но ее угол наклона винтовой линии обычно несколько велик (около 90 градусов), а ее корпус обычно довольно длинный в осевом направлении. Эти атрибуты придают ему черты винта. Различие между червяком и косозубой шестерней состоит в том, что по крайней мере один зуб остается для полного вращения вокруг спирали. Если это происходит, то это «червь»; если нет, то это «косозубая шестерня». У червя может быть всего один зуб. Если этот зуб сохраняется в течение нескольких оборотов по спирали, на поверхности у червя появляется более одного зуба, но на самом деле вы видите один и тот же зуб, появляющийся через определенные промежутки времени по длине червя. Применяется обычная номенклатура винта: однозубый червяк называется одиночный поток или одиночный старт; червь с более чем одним зубом называется несколько потоков или многократный запуск. Угол наклона спирали червяка обычно не указывается. Вместо этого дается угол подъема, равный 90 градусам минус угол наклона спирали.
В червячной передаче червяк всегда может управлять шестерней. Однако, если шестерня попытается запустить червяк, это может или не может быть успешным. В частности, если угол опережения небольшой, зубья шестерни могут просто сцепиться с зубьями червяка, потому что составляющая силы по окружности червяка недостаточна для преодоления трения. Однако в традиционных музыкальных шкатулках шестерня приводит в движение червяк, имеющий большой угол наклона спирали. Эта сетка приводит в движение лопатки ограничителя скорости, установленные на валу червяка.
Червячные передачи, которые блокируются, называются самоблокировка, что может быть использовано с пользой, например, когда требуется установить положение механизма, повернув червяк, а затем заставить механизм удерживать это положение. Примером может служить головка машины найдено на некоторых типах струнные инструменты.
Если шестерня в червячной передаче представляет собой обычную косозубую шестерню, достигается только одна точка контакта.[27][30] Если требуется передача мощности от средней до высокой, форма зуба шестерни изменяется для достижения более тесного контакта, заставляя обе шестерни частично охватывать друг друга. Для этого нужно сделать оба вогнутыми и соединить их точка перевала; это называется конус[31] или «Двойное обертывание».
Червячные передачи могут быть правыми или левыми, в соответствии с давно установившейся практикой для винтовой резьбы.[17]
Некруглый

Некруглые шестерни предназначены для специального назначения. В то время как обычная передача оптимизирована для передачи крутящего момента на другой зацепленный элемент с минимальным шумом и износом и максимальным эффективность, основная цель некруглого зубчатого колеса может быть соотношение вариации, смещение оси колебания и больше. Общие области применения включают текстильные машины, потенциометры и бесступенчатые трансмиссии.
Рейка и шестерня

А стойка представляет собой зубчатый стержень или стержень, который можно рассматривать как секторную шестерню с бесконечно большим радиус кривизны. Крутящий момент может быть преобразована в линейную силу путем зацепления стойки с круглой шестерней, называемой шестерня: шестерня вращается, а рейка движется по прямой. Такой механизм используется в автомобилях для преобразования вращения руль в движение слева направо тяга (s).
Стойки также используются в теории геометрии зубчатых колес, где, например, форма зуба сменного набора зубчатых колес может быть указана для зубчатой рейки (бесконечный радиус), а форма зуба для зубчатых колес конкретных фактических радиусов затем определяется из этого . Тип реечной передачи также используется в зубчатая железная дорога.
Эпициклический
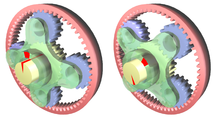
В планетарной передаче одна или несколько передач топоры движется. Примеры солнечная и планетарная передача (см. ниже), циклоидный драйв, автоматические трансмиссии, и механические дифференциалы.
Солнце и планета

Солнечная и планетарная передача это метод преобразования возвратно-поступательное движение в вращательное движение что использовалось в Паровые двигатели. Джеймс Ватт использовал его на своих первых паровых двигателях, чтобы обойти патент на заводить, но это также дало преимущество увеличения скорости маховика, поэтому Ватт мог использовать более легкий маховик.
На иллюстрации солнце желтое, планета красная, возвратно-поступательный рычаг синего цвета, маховик зеленый и карданный вал серый.
Гармоническая передача
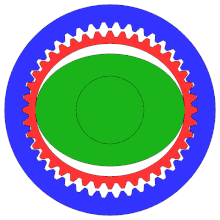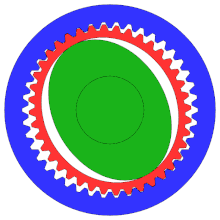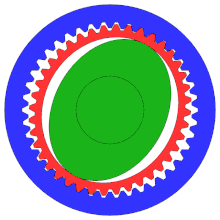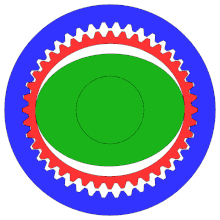
А гармоническая передача или зубчатая передача специализированный зубчатый механизм, часто используемый в промышленных управления движением, робототехника и аэрокосмический за его преимущества перед традиционными зубчатыми передачами, в том числе отсутствие люфта, компактность и высокие передаточные числа.
Хотя диаграмма не демонстрирует правильную конфигурацию, это «зубчатая передача», обычно с гораздо большим числом зубьев, чем у традиционной шестерни, чтобы обеспечить более высокую степень точности.
Клетка передач

А клетка передач, также называемый фонарь или фонарь шестерня, имеет цилиндрические стержни вместо зубьев, параллельные оси и расположенные по кругу вокруг нее, как стержни на круглой птичьей клетке или фонаре. Узел скрепляется дисками на каждом конце, в которые вставлены стержни зубьев и ось. Клеточные шестерни более эффективны, чем сплошные шестерни,[нужна цитата ] и грязь может падать сквозь стержни, а не застревать и увеличивать износ. Они могут быть изготовлены с помощью очень простых инструментов, так как зубья формируются не путем резки или фрезерования, а путем сверления отверстий и вставки стержней.
Иногда используется в часах, клетка передач всегда должен приводиться в движение зубчатым колесом, а не использоваться в качестве водителя. В клетка передач Первоначально консервативные производители часов не одобряли его. Он стал популярным в башенных часах, где грязные условия труда были наиболее распространенным явлением. Их часто использовали в отечественных американских часовых механизмах.
Циклоидальная передача
Магнитная передача
Все зубцы каждого зубчатого компонента магнитных зубчатых колес действуют как постоянный магнит с периодическим чередованием противоположных магнитных полюсов на сопряженных поверхностях. Компоненты редуктора установлены с люфт возможность аналогична другим механическим передачам. Хотя они не могут оказывать такое же усилие, как традиционные шестерни, такие шестерни работают, не касаясь друг друга, поэтому они невосприимчивы к износу, имеют очень низкий уровень шума и могут проскальзывать без повреждений, что делает их очень надежными.[32] Их можно использовать в конфигурациях, которые невозможны для шестерен, которые должны физически соприкасаться, и могут работать с неметаллическим барьером, полностью отделяющим движущую силу от нагрузки. В магнитная муфта может передавать силу в герметично запечатан корпус без использования радиальное уплотнение вала, который может протечь.
Номенклатура
Общее
- Вращательный частота, п
- Измеряется при вращении во времени, например число оборотов в минуту (Об / мин или об / мин).
- Угловая частота, ω
- Измеряется в радиан в секунду. 1 Об / мин = 2π рад / минута = π / 30 рад / сек.
- Количество зубьев, Н
- Сколько зубьев у шестерни, целое число. В случае червя это количество запусков потока, которое имеет червь.
- Шестерня
- Большая из двух взаимодействующих шестерен или отдельная шестерня.
- Шестерня
- Меньшая из двух взаимодействующих шестерен.
- Путь контакта
- Путь, по которому следует точка контакта между двумя зубьями зубчатой передачи.
- Линия действия, напорная линия
- Линия, по которой направлена сила между двумя зубьями шестерни. Он имеет то же направление, что и вектор силы. Как правило, линия действия меняется от момента к моменту в течение периода зацепления пары зубов. Для эвольвентные шестерни однако сила, действующая между зубцами, всегда направлена по одной и той же линии, то есть линия действия постоянна. Это означает, что для эвольвентных зубчатых колес путь контакта также является прямой линией, совпадающей с линией действия, что действительно имеет место.
- Ось
- Ось вращения шестерни; осевая линия вала.
- Точка подачи
- Точка, где линия действия пересекает линию, соединяющую две оси шестерен.
- Окружность поля, линия подачи
- Круг с центром и перпендикуляром к оси, проходящий через точку деления. Предварительно заданное диаметральное положение на зубчатом колесе, в котором определяются толщина круглого зуба, угол давления и углы винтовой линии.
- Диаметр шага, d
- Предварительно заданное диаметральное положение на зубчатом колесе, в котором определяются толщина круглого зуба, угол давления и углы винтовой линии. Стандартный делительный диаметр является расчетным размером и не может быть измерен, но это место, где производятся другие измерения. Его значение основано на количестве зубцов (N), нормальный модуль (мп; или нормальный диаметральный шаг, пd) и угол наклона спирали ():
- в метрических единицах или в имперских единицах.[33]
- Модуль или модуль, м
- Поскольку вычислять круговой шаг с помощью иррациональные числа инженеры-механики обычно используют коэффициент масштабирования, который заменяет его обычным значением. Это известно как модуль или модуль колеса и просто определяется как:
- где m - модуль, а p - круговой шаг. В единицы модуля обычно миллиметры; ан Английский модуль иногда используется с единицами измерения дюймы. Когда диаметральный шаг DP выражается в английских единицах,
- в условных метрических единицах.
- Расстояние между двумя осями становится:
- где a - расстояние до оси, z1 и z2 - количество зубцов (зубьев) для каждого из двух колес (шестерен). Эти числа (или хотя бы одно из них) часто выбирают среди простые числа чтобы создать равномерный контакт между каждой зубчатой шестерней обоих колес и тем самым избежать ненужного износа и повреждений. Равномерный износ шестерен достигается за счет того, что количество зубьев двух шестерен, находящихся в зацеплении, относительно простой друг другу; это происходит, когда наибольший общий делитель (НОД) числа каждого зуба шестерни равно 1, например НОД (16,25) = 1; если требуется передаточное число 1: 1, между двумя шестернями может быть вставлена относительно основная шестерня; это поддерживает передаточное отношение 1: 1, но меняет направление передачи; в этом случае может быть вставлена вторая относительно первичная шестерня для восстановления исходного направления вращения при сохранении равномерного износа всех 4 шестерен. Инженеры-механики, по крайней мере, в континентальной Европе, обычно используют модуль вместо кругового шага. Модуль, как и круговой шаг, можно использовать для всех типов зубчатых колес, а не только развиваться на основе прямых винтиков.[34]
- Диаметр рабочего шага
- Диаметр определяется количеством зубьев и межосевым расстоянием, на котором работают шестерни.[17] Пример шестерни:
- Поверхность поля
- В цилиндрических зубчатых колесах цилиндр образован выступом делительной окружности в осевом направлении. В более общем смысле, поверхность, образованная суммой всех делительных окружностей, движущихся вдоль оси. У конических шестерен - конус.
- Угол действия
- Угол с вершиной в центре шестерни, одна ножка находится в точке первого соприкосновения зубьев, а другая - в точке их расцепления.
- Арка действия
- Участок делительной окружности, ограниченный углом действия.
- Угол давления,
- Дополнение угла между направлением, в котором зубья действуют друг на друга, и линией, соединяющей центры двух шестерен. Для эвольвентных зубчатых колес зубья всегда оказывают усилие вдоль линии действия, которая для эвольвентных зубчатых колес является прямой линией; Таким образом, для эвольвентных зубчатых колес угол давления постоянен.
- Наружный диаметр,
- Диаметр шестерни, измеренный от вершин зубьев.
- Диаметр корня
- Диаметр шестерни, измеренный у основания зуба.
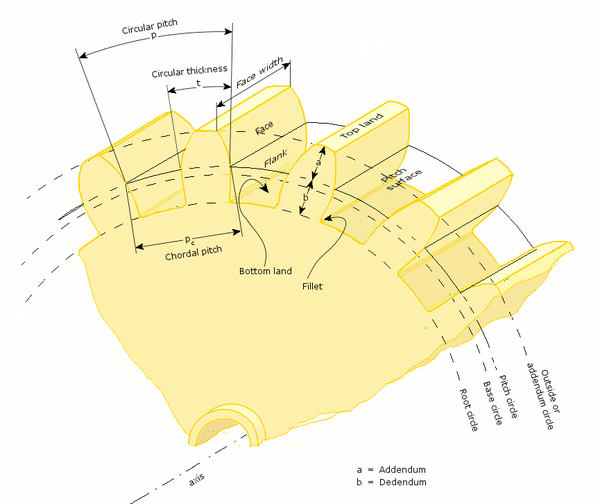
- Дополнение, а
- Радиальное расстояние от поверхности тангажа до крайней точки зуба.
- Dedendum, б
- Радиальное расстояние от глубины желоба зуба до поверхности поля.
- Вся глубина,
- Расстояние от верхушки зуба до корня; она равна добавке плюс вершина или рабочей глубине плюс зазор.
- Оформление
- Расстояние между корневой окружностью шестерни и добавочной окружностью ее ответной части.
- Рабочая глубина
- Глубина зацепления двух шестерен, то есть сумма их рабочих смещений.
- Круговой шаг, p
- Расстояние от одной поверхности зуба до соответствующей поверхности соседнего зуба той же шестерни, измеренное по делительной окружности.
- Диаметр диаметра, ДП
- Отношение количества зубьев к делительному диаметру. Может измеряться в зубах на дюйм или зубах на сантиметр, но обычно имеет единицы на дюйм диаметра. Где модуль, м, в метрических единицах
- в английских единицах
- Базовый круг
- В эвольвентных зубчатых колесах профиль зуба создается эвольвентой основной окружности. Радиус основной окружности несколько меньше радиуса делительной окружности.
- Базовый тон, нормальный тон,
- В эвольвентных зубчатых колесах - расстояние от одной поверхности зуба до соответствующей поверхности соседнего зуба той же шестерни, измеренное по основной окружности.
- Вмешательство
- Контакт между зубами за пределами предполагаемых частей их поверхностей
- Сменный набор
- Набор шестерен, каждая из которых правильно сочетается с любой другой.
Косозубая шестерня
- Угол наклона спирали,
- Угол между касательной к винтовой линии и осью шестерни. В предельном случае прямозубой шестерни он равен нулю, хотя его также можно рассматривать как угол гипотенузы.
- Нормальный круговой шаг,
- Круговой шаг в плоскости перпендикулярно зубам.
- Шаг поперечной окружности, p
- Круговой шаг в плоскости вращения шестерни. Иногда просто называют «круговой шаг».
Некоторые другие параметры спирали можно просматривать как в нормальной, так и в поперечной плоскостях. Нижний индекс n обычно указывает на нормальный.
Червячный редуктор
- Свинец
- Расстояние от любой точки резьбы до соответствующей точки на следующем витке той же резьбы, измеренное параллельно оси.
- Шаг линейный, p
- Расстояние от любой точки резьбы до соответствующей точки на соседней резьбе, измеренное параллельно оси. Для червяка с одной резьбой шаг и линейный шаг одинаковы.
- Угол подъема,
- Угол между касательной к спирали и плоскостью, перпендикулярной оси. Обратите внимание, что для косозубых зубчатых колес обычно указывается дополнение угла наклона винтовой линии.
- Диаметр шага,
- То же, что описано ранее в этом списке. Обратите внимание, что для червяка он по-прежнему измеряется в плоскости, перпендикулярной оси шестерни, а не в наклонной плоскости.
Индекс w обозначает червяк, индекс g обозначает шестерню.
Зубной контакт

Линия контакта
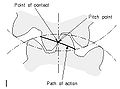
Путь действия

Линия действия
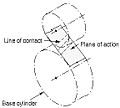
Самолет действия
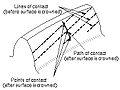
Линии контакта (косозубая передача)

Арка действия

Продолжительность действия
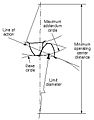
Предельный диаметр
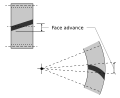
Продвижение лица

Зона действия
- Точка касания
- Любая точка, в которой два профиля зуба касаются друг друга.
- Линия контакта
- Линия или кривая, по которой две поверхности зуба касаются друг друга.
- Путь действия
- Географическое положение последовательных точек контакта между парой зубьев шестерни во время фазы зацепления. Для сопряженных зубьев шестерни путь действия проходит через точку тангажа. Это след поверхности действия в плоскости вращения.
- Линия действия
- Путь действия эвольвентных шестерен. Это прямая линия, проходящая через точку наклона и касательная к обеим базовым окружностям.
- Поверхность действия
- Воображаемая поверхность, на которой происходит контакт между двумя контактирующими поверхностями зубьев. Это суммирование путей действия во всех частях зубьев зацепления.
- Самолет действия
- Поверхность действия для эвольвентных шестерен с параллельными осями и прямозубых или косозубых зубьев. Он касается базовых цилиндров.
- Зона действия (контактная зона)
- Для эвольвентных зубчатых колес с параллельной осью и прямозубых или косозубых зубьев - это прямоугольная область в плоскости действия, ограниченная длиной действия и эффективным ширина лица.
- Путь контакта
- Кривая на любой поверхности зуба, вдоль которой происходит теоретический одноточечный контакт во время зацепления шестерен с корончатыми поверхностями зубьев или шестерен, которые обычно входят в зацепление только с одноточечным контактом.
- Продолжительность действия
- Расстояние на линии действия, через которое точка контакта перемещается во время действия профиля зуба.
- Дуга действия, Qт
- Дуга делительной окружности, по которой профиль зуба перемещается от начала до конца контакта с сопрягаемым профилем.
- Дуга подхода, Qа
- Дуга делительной окружности, по которой профиль зуба перемещается от начала контакта до точки контакта, достигающей точки деления.
- Дуга выемки, Qр
- Дуга делительной окружности, по которой профиль зуба перемещается от контакта в начальной точке до конца контакта.
- Коэффициент контакта, мc, ε
- Количество угловых шагов, на которые поверхность зуба поворачивается от начала до конца контакта. Проще говоря, его можно определить как меру среднего числа зубьев, находящихся в контакте в течение периода, в течение которого зуб выходит из контакта с сопряженной шестерней.
- Коэффициент поперечного контакта, мп, εα
- Коэффициент контакта в поперечной плоскости. Это отношение угла действия к угловому шагу. Для эвольвентных зубчатых колес он наиболее точно определяется как отношение длины хода к основному шагу.
- Коэффициент лобового контакта, мF, εβ
- Коэффициент контакта в аксиальной плоскости или отношение ширины грани к осевому шагу. Для конических и гипоидных зубчатых колес это отношение забоя к круговому шагу.
- Общее контактное отношение, мт, εγ
- Сумма отношения поперечного контакта и отношения торца контакта.
- Модифицированное соотношение контактов, мо
- Для конических зубчатых колес - квадратный корень из суммы квадратов коэффициентов поперечного и торцевого контакта.
- Предельный диаметр
- Диаметр шестерни, при котором линия действия пересекает максимальную (или минимальную для внутренней шестерни) добавочную окружность сопряженной шестерни. Это также называется началом активного профиля, началом контакта, концом контакта или концом активного профиля.
- Начало активного профиля (SAP)
- Пересечение предельного диаметра и эвольвентного профиля.
- Продвижение лица
- Расстояние на делительной окружности, через которую проходит спиральный или спиральный зубец из положения, в котором контакт начинается на одном конце следа зуба на делительной поверхности, до положения, в котором контакт прекращается на другом конце.
Толщина зуба

Толщина зуба

Соотношение толщины
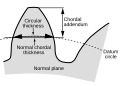
Толщина хорды

Измерение толщины зуба по штифту

Измерение диапазона

Длинные и короткие придаточные зубы
- Круглая толщина
- Длина дуги между двумя сторонами зуба шестерни на указанной исходный круг.
- Толщина поперечного круга
- Толщина круга в поперечной плоскости.
- Нормальная круглая толщина
- Толщина окружности в нормальной плоскости. В косозубой передаче это можно рассматривать как длину дуги вдоль нормальной спирали.
- Осевая толщина
- В косозубых передачах и червяках - толщина зуба в осевом поперечном сечении при стандартном продольном диаметре.
- Базовая круговая толщина
- В эвольвентных зубах - длина дуги на основной окружности между двумя эвольвентными кривыми, образующая профиль зуба.
- Нормальная толщина хорд
- Длина хорды, которая образует дугу толщины окружности в плоскости, перпендикулярной продольной спирали. Может быть выбран любой удобный измерительный диаметр, не обязательно стандартный делительный диаметр.
- Chordal addendum (высота хорды)
- Высота от вершины зуба до хорды, пересекающей дугу толщины окружности. Может быть выбран любой удобный измерительный диаметр, не обязательно стандартный делительный диаметр.
- Сдвиг профиля
- Смещение базовой стойки базовая линия из эталонного цилиндра, сделанного безразмерным путем деления на нормальный модуль. Он используется для указания толщины зуба, часто для нулевого люфта.
- Сдвиг стойки
- Смещение базовой линии инструмента от опорного цилиндра, сделанного безразмерным путем деления нормального модуля. Используется для указания толщины зуба.
- Измерение по штифтам
- Измерение расстояния, проведенного над штифтом, расположенным в пространстве между зубьями и контрольной поверхностью. Контрольной поверхностью может быть контрольная ось шестерни, исходная поверхность либо один или два штифта, расположенные в пространстве между зубьями или пространствах напротив первого. Это измерение используется для определения толщины зуба.
- Измерение диапазона
- Измерение расстояния между несколькими зубами в нормальной плоскости. Пока измерительное устройство имеет параллельные измерительные поверхности, которые соприкасаются с немодифицированной частью эвольвенты, измерение будет проводиться по линии, касательной к основному цилиндру. Используется для определения толщины зуба.
- Модифицированные придаточные зубы
- Зубья шестерни включения, одна или обе имеют нестандартные приспособления.
- Зубы полной глубины
- Зубья, у которых рабочая глубина равна 2.000, деленным на нормальный диаметральный шаг.
- Короткие зубы
- Зубья, в которых рабочая глубина меньше 2.000 деленных на нормальный диаметральный шаг.
- Равные придаточные зубы
- Зубья, в которых две зацепляющие шестерни имеют одинаковые сростки.
- Длинные и короткие придаточные зубы
- Зубья, в которых сращения двух зацепляющих шестерен неравные.
Подача
Подача расстояние между точкой на одном зубе и соответствующей точкой на соседнем зубе.[17] Это размер, измеряемый вдоль линии или кривой в поперечном, нормальном или осевом направлениях. Использование одного слова подача без уточнения может быть неоднозначным, и по этой причине предпочтительно использовать специальные обозначения, такие как поперечный круговой шаг, нормальный базовый шаг, осевой шаг.
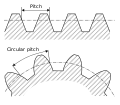
Подача
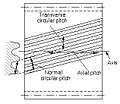
Шаг зуба

Отношения основного тона
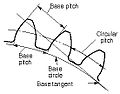
Основные передачи
- Круговой шаг, п
- Расстояние дуги по заданной делительной окружности или делительной линии между соответствующими профилями соседних зубьев.
- Поперечный круговой шаг, пт
- Круговой шаг в поперечной плоскости.
- Нормальный круговой шаг, пп, пе
- Шаг окружности в нормальной плоскости, а также длина дуги по винтовой линии с нормальным шагом между зубьями или резьбой.
- Осевой шаг, пИкс
- Линейный шаг в осевой плоскости и на продольной поверхности. В косозубых зубчатых колесах и червяках осевой шаг одинаков на всех диаметрах. В зубчатых передачах других типов осевой шаг может быть ограничен поверхностью наклона и может быть круглым. Термин осевой шаг предпочтительнее термина линейный шаг. Осевой шаг винтового червяка и круговой шаг его червячной передачи одинаковы.
- Нормальный базовый шаг, пN, пмлрд
- Эвольвентная косозубая передача - это базовый шаг в нормальной плоскости. Это нормальное расстояние между параллельными спиральными эвольвентными поверхностями на плоскости действия в нормальной плоскости или длина дуги на нормальной базовой спирали. Это постоянное расстояние в любой косозубой эвольвентной передаче.
- Поперечный шаг основания, пб, пbt
- В эвольвентной передаче шаг находится на основной окружности или вдоль линии действия. Соответствующие стороны зубьев эвольвентной шестерни представляют собой параллельные кривые, а базовый шаг - это постоянное и фундаментальное расстояние между ними по общей нормали в поперечной плоскости.
- Диаметр диаметра (поперечный), пd
- Отношение количества зубьев к стандартному продольному диаметру в дюймах.
- Нормальный диаметральный шаг, пnd
- Величина диаметрального шага в нормальной плоскости косозубой передачи или червяка.
- Угловой шаг, θN, τ
- Угол, образованный круговым шагом, обычно выражается в радианах.
- степени или радианы
Люфт
Люфт ошибка движения, возникающая при изменении направления передачи. Он существует потому, что всегда существует некоторый зазор между задней поверхностью ведущего зуба и передней поверхностью зуба за ним на ведомой шестерне, и этот зазор должен быть закрыт, прежде чем сила может быть передана в новом направлении. Термин «люфт» также может использоваться для обозначения размера зазора, а не только для явления, которое он вызывает; таким образом, можно сказать, что пара шестерен имеет, например, «люфт 0,1 мм». Пара шестерен может быть спроектирована с нулевым люфтом, но это предполагает совершенство производства, однородные характеристики теплового расширения во всей системе и отсутствие смазки. Следовательно, зубчатые пары рассчитаны на некоторый люфт. Обычно это достигается за счет уменьшения толщины зуба каждой шестерни на половину желаемого зазора. Однако в случае большой шестерни и маленькой шестерни люфт обычно полностью снимается с шестерни, и шестерня получает зубья полного размера. Люфт также может быть обеспечен за счет большего разведения шестерен. Обратная реакция зубчатая передача равняется сумме люфта каждой пары шестерен, поэтому в длинных поездах люфт может стать проблемой.
В ситуациях, требующих точности, таких как контрольно-измерительные приборы и управление, люфт можно минимизировать с помощью одного из нескольких методов. Например, шестерня может быть разделена вдоль плоскости, перпендикулярной оси, одна половина прикреплена к валу обычным образом, а другая половина размещена рядом с ним, чтобы свободно вращаться вокруг вала, но с пружинами между двумя половинами, обеспечивающими относительную крутящий момент между ними, так что фактически получается одно зубчатое колесо с расширяющимися зубьями. Другой метод заключается в сужении зубьев в осевом направлении и обеспечении скольжения шестерни в осевом направлении для компенсации провисания.
Переключение передач
В некоторых машинах (например, автомобилях) необходимо изменять передаточное число в соответствии с задачей, этот процесс известен как переключение передач или переключение передач. Есть несколько способов переключения передач, например:
- Механическая коробка передач
- Автоматическая коробка передач
- Шестерни переключателя, которые на самом деле звездочки в сочетании с роликовая цепь
- Ступичные шестерни (также называемые планетарными передачами или солнечно-планетарными передачами)
Есть несколько результатов переключения передач в автомобилях. На случай, если уровень шума автомобиля, есть более высокие уровни звука выдается, когда автомобиль включен на пониженную передачу. Расчетный срок службы шестерен с меньшим передаточным числом короче, поэтому можно использовать более дешевые шестерни, которые имеют тенденцию генерировать больше шума из-за меньшего отношения перекрытия и более низкой жесткости зацепления и т. Д., Чем косозубые шестерни, используемые для высоких передаточных чисел. Этот факт использовался для анализа звука, создаваемого транспортными средствами, с конца 1960-х годов и был включен в моделирование шума городских дорог и соответствующий дизайн городских шумовые барьеры вдоль проезжей части.[35]
Профиль зуба

Профиль прямозубой шестерни
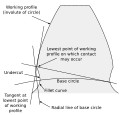
Подрез
Профиль - это одна сторона зуба в поперечном сечении между внешней окружностью и корневой окружностью. Обычно профиль - это кривая пересечения поверхности зуба и плоскости или поверхности, перпендикулярной к поверхности наклона, такой как поперечная, нормальная или осевая плоскость.
Кривая скругления (корневая кромка) - это вогнутая часть профиля зуба, где она соединяется с нижней частью пространства зуба.2
Как упоминалось в начале статьи, достижение непеременного отношения скоростей зависит от профиля зубьев.Трение и износ между двумя шестернями также зависит от профиля зуба. Существует множество профилей зубьев, обеспечивающих постоянное соотношение скоростей. Во многих случаях, учитывая произвольную форму зуба, можно разработать профиль зуба ответной шестерни, который обеспечивает постоянное передаточное отношение. Однако в наше время наиболее часто используются два профиля зубьев с постоянной скоростью: циклоида и эвольвента. Циклоида была более распространена до конца 1800-х годов. С тех пор эвольвента в значительной степени вытеснила ее, особенно в приводах. В некотором смысле циклоида является более интересной и гибкой формой; однако эвольвента имеет два преимущества: ее легче изготавливать и она позволяет изменять расстояние между центрами шестерен в некотором диапазоне без нарушения постоянства передаточного отношения. Циклоидные шестерни работают правильно только при правильном межосевом расстоянии. Циклоидальные шестерни все еще используются в механических часах.
An подрезать - состояние сформированных зубьев шестерни, когда любая часть кривой галтеля находится внутри линии, касательной к рабочему профилю в точке соединения с галтелем. Поднутрение может быть сделано намеренно для облегчения чистовых операций. С поднутрением кривая сопряжения пересекает рабочий профиль. Без поднутрения кривая сопряжения и рабочий профиль имеют общую касательную.
Зубчатые материалы

При производстве шестерен используются многочисленные цветные сплавы, чугуны, порошковая металлургия и пластмассы. Однако чаще всего используются стали из-за их высокого отношения прочности к весу и низкой стоимости. Пластик обычно используется там, где важна цена или вес. Правильно спроектированная пластиковая шестерня может заменить стальную во многих случаях, потому что она обладает многими желательными свойствами, включая устойчивость к загрязнениям, низкоскоростное зацепление, способность довольно хорошо «проскакивать».[36] и возможность изготавливаться из материалов, не нуждающихся в дополнительной смазке. Производители использовали пластиковые шестерни для снижения затрат на потребительские товары, включая копировальные машины, оптические запоминающие устройства, дешевые динамо-машины, бытовое аудиооборудование, серводвигатели и принтеры. Еще одним преимуществом использования пластмасс ранее (например, в 1980-х годах) было снижение затрат на ремонт некоторых дорогих машин. В случае сильного замятия (например, бумаги в принтере) пластмассовые зубья шестерни будут оторваны от подложки, позволяя приводному механизму затем свободно вращаться (вместо того, чтобы повредить себя, пытаясь противостоять замятию). Такое использование «жертвенных» зубьев шестерни позволило избежать разрушения гораздо более дорогого двигателя и связанных с ним деталей. В более поздних конструкциях этот метод был заменен использованием муфт и двигателей с ограничением крутящего момента или тока.
Стандартные шаги и модульная система
Хотя шестерни могут изготавливаться с любым шагом, для удобства и взаимозаменяемости часто используются стандартные шаги. Шаг - это свойство, связанное с линейным Габаритные размеры и поэтому отличается от того, находятся ли стандартные значения в имперский (дюйм) или метрика системы. С помощью дюйм замеров выбраны стандартные значения диаметрального шага с единицей измерения «на дюйм»; то диаметральный шаг - количество зубьев шестерни с делительным диаметром один дюйм. Стандартные стандартные значения для цилиндрических зубчатых колес: 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 48, 64, 72, 80, 96, 100, 120 и 200.[37] Некоторые стандартные высоты звука, такие как 1/10 и 1/20 в дюймах, которые связаны с линейной стойкой, на самом деле (линейные) круговой шаг значения в дюймах[37]
Когда размеры шестерен в метрической системе, шаг обычно выражается в модуль или модуль, что фактически является измерением длины по средний диаметр. Под модулем понимается деленный на число зубьев средний диаметр в миллиметрах. Когда модуль основан на дюймовых измерениях, он известен как Английский модуль чтобы избежать путаницы с метрическим модулем. Модуль - это прямой размер, в отличие от диаметрального шага, который является обратным размером («количество ниток на дюйм»). Таким образом, если делительный диаметр шестерни составляет 40 мм, а количество зубьев 20, модуль равен 2, что означает, что на каждый зуб приходится 2 мм делительного диаметра.[38] Предпочтительные стандартные значения модуля: 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,8, 1,0, 1,25, 1,5, 2,0, 2,5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40 и 50.[39]
Производство
По состоянию на 2014 год около 80% всех зубчатых передач, производимых в мире, производятся чистая форма литье. Формованная передача обычно либо порошковая металлургия или пластик.[40] Многие шестерни уже готовы, когда они покидают форму (в том числе литье под давлением пластик и литье под давлением металлические шестерни), но порошковые металлические шестерни требуют спекание и отливки из песка или отливки по выплавляемым моделям требовать зуборезный или другой механическая обработка чтобы закончить их. Наиболее распространенная форма зуборезной обработки - стружка, но формирование зубчатых колес, фрезерование, и протяжка тоже существуют. 3D печать как метод производства быстро расширяется. Для металлических шестерен в передачи легковых и грузовых автомобилей, зубы термически обработанный сделать их трудными и многое другое износостойкий оставляя сердцевину мягкой и жесткий. Для больших шестерен, склонных к короблению, закалочный пресс используется.
Модель шестеренки в современной физике
Современная физика по-разному переняли зубчатую модель. В девятнадцатом веке, Джеймс Клерк Максвелл разработал модель электромагнетизм в котором силовые линии магнитного поля были вращающимися трубками несжимаемой жидкости. Максвелл использовал зубчатое колесо и назвал его «холостым колесом», чтобы объяснить электрический ток как вращение частиц в направлении, противоположном направлению вращающихся силовых линий.[41]
В последнее время, квантовая физика использует в своей модели «квантовые шестеренки». Группа шестерен может служить моделью для нескольких различных систем, таких как искусственно созданное наномеханическое устройство или группа кольцевых молекул.[42]
В трехволновая гипотеза сравнивает дуальность волна-частица к конической передаче.[43]
Зубчатый механизм в мире природы

Механизм передач ранее считался исключительно искусственным, но в 2013 году ученые из Кембриджский университет объявили о своем открытии, что ювенильная форма обычного насекомого Issus (виды Иссус колеоптратус ), найденный во многих европейских садах, имеет зубчатый механизм на задних лапах. Каждая ножка имеет полосу зубьев 400 микрометров, радиус шага 200 микрометров, с 10-12 полностью сцепленными зубьями прямозубой шестерни, включая филе изгибы у основания каждого зуба, чтобы снизить риск порезов.[44] Шарнир вращается, как механические шестерни, и синхронизирует Иссуса задние лапы при прыжке с точностью до 30 микросекунд, предотвращая рыскание.[45][46][47][48] Шестерни не всегда включаются. Один расположен на каждой из задних лап молодого насекомого, и когда оно готовится к прыжку, два набора зубов сцепляются вместе. В результате лапы двигаются почти в унисон, давая насекомому больше мощности, поскольку шестерни вращаются до точки остановки, а затем разблокируются.[45]
Смотрите также
использованная литература
- ^ «Определение GEAR». www.merriam-webster.com. Получено 20 сентября 2018.
- ^ «Основы трансмиссии». Как это работает.
- ^ Дерек Дж. Де Солла Прайс, О происхождении часового механизма, вечных двигателей и компаса, стр.84
- ^ «Проект исследования антикиферского механизма: почему это так важно?». Архивировано из оригинал 4 мая 2012 г.. Получено 10 января 2011.
Считается, что этот механизм датируется периодом между 150 и 100 годом до нашей эры.
- ^ Нортон 2004, п. 462
- ^ Льюис, М. Дж. Т. (1993). «Шестерни в Древнем мире». Стремление. 17 (3): 110–115. Дои:10.1016 / 0160-9327 (93) 90099-О.
- ^ «Сегментная передача». thefreedictionary.com. Получено 20 сентября 2018.
- ^ а б Дональд Хилл (2012), Книга знаний об изобретательных механических устройствах, стр. 273, Springer Science + Business Media
- ^ а б Ирфан Хабиб, Экономическая история средневековой Индии, 1200-1500 гг., стр. 53, Pearson Education
- ^ Джозеф Нидхэм (1986). Наука и цивилизация в Китае: Том 4, Часть 2, стр. 298. Тайбэй: Caves Books, Ltd.
- ^ "Астролябия Мухаммада Ибн Аби Бакра Аль Исфахани".
- ^ "шестерня (сущ.)". Etymonline. Получено 13 февраля 2020.
- ^ "Этимология 1: Винтик (существительное)". Викисловарь. Получено 29 июля 2019.
- ^ "винтик (сущ.)". Etymonline. Получено 13 февраля 2020.
- ^ Грант, Джордж Б. (1893). Трактат о зубчатых колесах (6-е, илл. Ред.). Лексингтон, Массачусетс; Филадельфия, Пенсильвания: Джордж Б. Грант. п.21.
- ^ Радзевич, Стивен П. (2012). Справочник Дадли по разработке и производству практического оборудования (PDF) (2-е изд.). Бока-Ратон, Флорида: CRC Press, компания Taylor & Francis Group. С. 691, 702.
- ^ а б c d Американская ассоциация производителей шестерен; Американский национальный институт стандартов, Номенклатура передач, определения терминов с символами (ANSI / AGMA 1012-G05 ed.), Американская ассоциация производителей шестерен
- ^ "Как работает Gears". howstuffworks.com. 16 ноября 2000 г.. Получено 20 сентября 2018.
- ^ Справочник по машинам. Нью-Йорк: Промышленная пресса. 2012. С.2125. ISBN 978-0-8311-2900-2.
- ^ Хурми, Р.С., Теория машин, С.ЧАНД
- ^ Шунк, Ричард, «Минимизация шума коробки передач внутри и снаружи коробки», Дизайн систем движения.
- ^ Vallance & Doughtie 1964, п. 281
- ^ а б Косозубые шестерни, заархивировано из оригинал 26 июня 2009 г., получено 15 июн 2009.
- ^ Макгроу-Хилл 2007, п. 742.
- ^ Кэнфилд, Стивен (1997), «Типы снаряжения», Динамика машин, Технический университет Теннесси, факультет машиностроения, лекции ME 362, архив из оригинал 29 августа 2008 г.
- ^ Гильберт, Дэвид; Кон-Фоссен, Стефан (1952), Геометрия и воображение (2-е изд.), Нью-Йорк: Челси, стр. 287, г. ISBN 978-0-8284-1087-8.
- ^ а б Макгроу-Хилл 2007, п. 743.
- ^ Vallance & Doughtie 1964, п. 287.
- ^ Vallance & Doughtie 1964 С. 280, 296.
- ^ Vallance & Doughtie 1964, п. 290.
- ^ Макгроу-Хилл 2007, п. 744
- ^ Кравченко А.И., Бовда А.М. Шестерня с магнитной парой. Пат. Украины Н. 56700 - Бул. №2, 2011 - F16H 49/00.
- ^ ISO / DIS 21771: 2007: «Зубчатые колеса. Цилиндрические эвольвентные зубчатые колеса и зубчатые пары. Концепции и геометрия», Международная организация по стандартизации, (2007)
- ^ Гуннар Дальвиг, «Элементы конструкции и машиностроение», Конструктионэлемент и маска (на шведском языке), 7, ISBN 978-9140115546
- ^ Хоган, К. Майкл; Латшоу, Гэри Л. (21–23 мая 1973 г.). Связь между планировкой автомагистрали и городским шумом. Труды ASCE, Специальная конференция отдела городского транспорта. Чикаго, Иллинойс: Американское общество инженеров-строителей, Отдел городского транспорта.
- ^ Смит, Зан (2000), «Пластиковые шестерни более надежны, если инженеры учитывают свойства материалов и производственные процессы во время проектирования»., Дизайн систем движения.
- ^ а б "Справочное руководство W. M. Berg Gear" (PDF). Архивировано из оригинал (PDF) 21 апреля 2015 г.
- ^ Oberg, E .; Jones, F.D .; Horton, H.L .; Райффелл, Х. Х. (2000), Справочник по машинам (26-е изд.), Industrial Press, стр. 2649, ISBN 978-0-8311-2666-7.
- ^ «Элементы метрической зубчатой техники» (PDF).
- ^ Фред Эберли (август 2014 г.). "Материальное значение". Решения для передач: 22.
- ^ Сигел, Дэниел М. (1991). Инновация в электромагнитной теории Максвелла: молекулярные вихри, ток смещения и свет. Издательство Чикагского университета. ISBN 978-0521353656.
- ^ Маккиннон, Ангус (2002). «Квантовые шестерни: простая механическая система в квантовом режиме». Нанотехнологии. 13 (5): 678–681. arXiv:cond-mat / 0205647. Bibcode:2002Нанот..13..678М. Дои:10.1088/0957-4484/13/5/328. S2CID 14994774.
- ^ Сандук, М. И. (2007). «Подразумевает ли трехволновая гипотеза скрытая структура?» (PDF). Апейрон. 14 (2): 113–125. Bibcode:2007 Апеи ... 14..113с.
- ^ Стромберг, Джозеф (12 сентября 2013 г.), «У этого насекомого единственные механические механизмы, которые когда-либо встречались в природе», Смитсоновский журнал, получено 18 ноября 2020
- ^ а б Робертсон, Ади (12 сентября 2013 г.). «Первые в мире шестеренки, встречающиеся в природе, найдены на ногах насекомых». Грани. Получено 14 сентября 2013.
- ^ Функционирующие `` механические шестерни '' впервые наблюдаются в природе, Кембриджский университет, 2013.
- ^ Функционирующие `` механические шестерни '' впервые наблюдаются в природе, PHYS.ORG, Кембриджский университет
- ^ Берроуз, Малькольм; Саттон, Грегори (13 сентября 2013 г.). «Взаимодействующие шестерни синхронизируют движущие силы ног прыгающего насекомого». Наука. 341 (6151): 1254–1256. Дои:10.1126 / наука.1240284. HDL:1983 / 69cf1502-217a-4dca-a0d3-f8b247794e92. PMID 24031019. S2CID 24640726.
Список используемой литературы
- Макгроу-Хилл (2007), Энциклопедия науки и техники Макгроу-Хилла (10-е изд.), McGraw-Hill Professional, ISBN 978-0-07-144143-8.
- Нортон, Роберт Л. (2004), Дизайн машин (3-е изд.), McGraw-Hill Professional, ISBN 978-0-07-121496-4.
- Валланс, Алекс; Даути, Вентон Леви (1964), Конструкция элементов станка (4-е изд.), McGraw-Hill.
- Industrial Press (2012), Справочник по машинному оборудованию (29-е изд.), ISBN 978-0-8311-2900-2
- Инженеры Edge, дизайн шестерен и технические данные.
дальнейшее чтение
- Американская ассоциация производителей шестерен; Американский национальный институт стандартов (2005 г.), Номенклатура передач: определения терминов с символами (ANSI / AGMA 1012-F90 ed.), Американская ассоциация производителей зубчатых колес, ISBN 978-1-55589-846-5.
- Букингем, Эрл (1949), Аналитическая механика шестерен, McGraw-Hill Book Co ..
- Кой, Джон Дж .; Townsend, Dennis P .; Зарецкий, Эрвин В. (1985), Передача (PDF), НАСА Отделение научно-технической информации, NASA-RP-1152; Технический отчет AVSCOM 84-C-15.
- Кравченко А.И., Бовда А.М. Шестерня с магнитной парой. Пат. Украины Н. 56700 - Бул. №2, 2011 - F16H 49/00.
- Склейтер, Нил. (2011). «Шестерни: устройства, приводы и механизмы». Справочник по механизмам и механическим устройствам. 5-е изд. Нью-Йорк: Макгроу Хилл. С. 131–174. ISBN 9780071704427. Чертежи и конструкции различных передач.
- «Колеса, которые не скользят». Популярная наука, Февраль 1945 г., стр. 120–125.
внешние ссылки
- Геарариум. Музей шестерен и зубчатых колес - старинные и старинные шестерни, звездочки, трещотки и другие предметы, связанные с шестернями.
- Кинематические модели для цифровой библиотеки дизайна (KMODDL) - фильмы и фотографии сотен работающих моделей Корнельского университета
- Краткий исторический отчет о применении аналитической геометрии к форме зубьев шестерни
- Математический учебник для зубчатых передач (относящихся к робототехнике)
- Американская ассоциация производителей шестерен
- Gear Technology, журнал по производству зубчатых колес



















































