Рабочая функция - Work function

В физика твердого тела, то рабочая функция (иногда пишется рабочая функция) - минимум термодинамическая работа (т. е. энергия), необходимая для удаления электрон от твердого тела до точки в вакуум сразу за твердой поверхностью. Здесь «немедленно» означает, что конечное положение электрона находится далеко от поверхности в атомном масштабе, но все еще слишком близко к твердому телу, чтобы на него влияли окружающие электрические поля в вакууме. Работа выхода не является характеристикой объемного материала, а скорее свойство поверхности материала (в зависимости от поверхности кристалла и загрязнения).

Определение

Рабочая функция W для данной поверхности определяется разностью[1]

где −е это ответственность электрон, ϕ это электростатический потенциал в вакууме у поверхности, и EF это Уровень Ферми (электрохимический потенциал электронов) внутри материала. Период, термин −eϕ - энергия электрона, покоящегося в вакууме у поверхности.

График уровней энергии электронов в зависимости от положения в системе золото-вакуум-алюминий. Два изображенных здесь металла находятся в полном термодинамическом равновесии. Однако вакуум электростатический потенциал ϕ не плоский из-за разницы в работе.

На практике можно напрямую контролировать EF напряжением, приложенным к материалу через электроды, и работа выхода, как правило, является фиксированной характеристикой материала поверхности. Следовательно, это означает, что при приложении напряжения к материалу электростатический потенциал ϕ создаваемое в вакууме будет несколько ниже приложенного напряжения, разница будет зависеть от работы выхода поверхности материала. Преобразуя приведенное выше уравнение, мы получаем

где V = −EF/е напряжение материала (измеренное вольтметр, через присоединенный электрод) относительно электрическое заземление который определяется как имеющий нулевой уровень Ферми. Дело в том, что ϕ зависит от поверхности материала означает, что пространство между двумя разнородными проводниками будет иметь встроенный электрическое поле, когда эти проводники находятся в полном равновесии друг с другом (электрически закорочены друг с другом и имеют равные температуры). Пример такой ситуации изображен на рисунке рядом. Как описано в следующем разделе, эти встроенные вакуумные электрические поля в некоторых случаях могут иметь важные последствия.

Приложения

Термоэлектронная эмиссия
В термоэлектронной электронные пушки, работа выхода и температура горячий катод являются критическими параметрами при определении силы тока, который может быть испущен. Вольфрам, обычный выбор для нитей для вакуумных трубок, может выдерживать высокие температуры, но его излучение несколько ограничено из-за его относительно высокой работы выхода (примерно 4,5 эВ). Покрывая вольфрам веществом с более низкой работой выхода (например, торий или оксид бария ) эмиссия может быть значительно увеличена. Это продлевает срок службы нити накала, позволяя работать при более низких температурах (дополнительную информацию см. горячий катод ).
Гибка ленты модели в твердотельной электронике
Поведение твердотельного устройства сильно зависит от размера различных Барьеры Шоттки и смещения полос в местах соединения различных материалов, таких как металлы, полупроводники и изоляторы. Некоторые часто используемые эвристические подходы для прогнозирования выравнивания полос между материалами, например Правило Андерсона и Правило Шоттки-Мотта, основаны на мысленном эксперименте двух материалов, соединяющихся в вакууме, так что поверхности заряжаются и регулируют свои рабочие функции, чтобы стать равными непосредственно перед контактом. В действительности эти эвристики работы выхода неточны из-за пренебрежения многочисленными микроскопическими эффектами. Однако они обеспечивают удобную оценку до тех пор, пока истинное значение не может быть определено экспериментально.[2][3]
Равновесные электрические поля в вакуумных камерах
Различие работы выхода между разными поверхностями вызывает неоднородный электростатический потенциал в вакууме. Даже на якобы однородной поверхности колебания W потенциалы пятна всегда присутствуют из-за микроскопических неоднородностей. Патч-потенциалы нарушили работу чувствительного устройства, которое полагается на идеально однородный вакуум, например Сила Казимира эксперименты[4] и Гравитационный зонд B эксперимент.[5] Критическое устройство может иметь поверхности, покрытые молибденом, который показывает низкие различия в работе выхода между различными гранями кристалла.[6]
Контактная электрификация
Если две проводящие поверхности перемещаются относительно друг друга, а в пространстве между ними есть разность потенциалов, то возникает электрический ток. Это потому, что поверхностный заряд на проводнике зависит от величины электрического поля, которое, в свою очередь, зависит от расстояния между поверхностями. Внешне наблюдаемые электрические эффекты являются наибольшими, когда проводники разделены наименьшим расстоянием без соприкосновения (при контакте заряд вместо этого будет течь внутри через соединение между проводниками). Поскольку два проводника в равновесии могут иметь встроенную разность потенциалов из-за разницы работы выхода, это означает, что приведение разнородных проводников в контакт или их разведение приведет к возникновению электрических токов. Эти контактные токи могут повредить чувствительную микроэлектронную схему и возникать даже тогда, когда проводники будут заземлены в отсутствие движения.[7]

Измерение

Некоторые физические явления очень чувствительны к значению работы выхода. Наблюдаемые данные по этим эффектам могут быть приспособлены к упрощенным теоретическим моделям, что позволяет извлечь значение работы выхода. Эти феноменологически извлеченные функции выхода могут немного отличаться от термодинамическое определение, данное выше. Для неоднородных поверхностей работа выхода варьируется от места к месту, и разные методы будут давать разные значения типичной «работы выхода», поскольку они усредняют или по-разному выбирают микроскопические функции выхода.[8]

Многие методы были разработаны на основе различных физических эффектов для измерения работы выхода электронного образца. Можно выделить две группы экспериментальных методов измерения работы выхода: абсолютные и относительные.

  • В абсолютных методах используется электронная эмиссия из образца, вызванная поглощением фотонов (фотоэмиссия), высокой температурой (термоэлектронная эмиссия), вызванной электрическим полем (полевая электронная эмиссия ) или используя электронное туннелирование.
  • Относительные методы используют контактная разность потенциалов между образцом и электродом сравнения. Экспериментально используется либо анодный ток диода, либо измеряется ток смещения между образцом и эталоном, созданный искусственным изменением емкости между ними ( Кельвин Зонд метод Зондовый силовой микроскоп Кельвина ). Однако абсолютные значения работы выхода могут быть получены, если наконечник сначала откалиброван по эталонному образцу.[9]

Методы, основанные на термоэлектронной эмиссии

Работа выхода важна в теории термоэлектронная эмиссия, где тепловые флуктуации обеспечивают достаточно энергии для «испарения» электронов из горячего материала (называемого «эмиттером») в вакуум. Если эти электроны поглощаются другим, более холодным материалом (называемым коллекционер) то измеримое электрический ток будет соблюдаться. Термоэлектронная эмиссия может использоваться для измерения работы выхода как горячего эмиттера, так и холодного коллектора. Как правило, эти измерения включают подгонку к Закон Ричардсона, поэтому они должны выполняться в низкотемпературном и слаботочном режиме, где космический заряд эффекты отсутствуют.

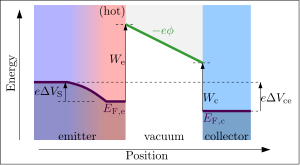
Диаграммы уровней энергии для термоэмиссионный диод в прямое смещение конфигурация, используемая для извлечения всех горячих электронов, выходящих с поверхности эмиттера. Барьер - это вакуум у поверхности эмиттера.

Для перехода от горячего эмиттера в вакуум энергия электрона должна превышать уровень Ферми эмиттера на величину

определяется просто термоэлектронной работой выхода эмиттера. Если электрическое поле приложено к поверхности эмиттера, то все вылетающие электроны будут ускоряться от эмиттера и поглощаться любым материалом, который прикладывает электрическое поле. Закон Ричардсона испускаемый плотность тока (на единицу площади излучателя), Jе (А / м2), относится к абсолютному температура Те эмиттера по уравнению:

где k это Постоянная Больцмана и константа пропорциональности Ае это Постоянная Ричардсона эмиттера, при этом зависимость Jе на Те может быть приспособлен к урожаю Wе.

Работа выхода холодного коллектора электронов

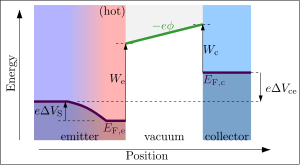
Диаграммы уровней энергии для термоэмиссионный диод в замедляющий потенциал конфигурация. Барьер - это вакуум у поверхности коллектора.

Эту же установку можно использовать для измерения работы выхода в коллекторе, просто регулируя приложенное напряжение. далеко от эмиттер, то большая часть электронов, выходящих из эмиттера, просто отражается обратно к эмиттеру. Только электроны с наивысшей энергией будут иметь достаточно энергии, чтобы достичь коллектора, а высота потенциального барьера в этом случае зависит от работы выхода коллектора, а не эмиттера.

Течение по-прежнему регулируется законом Ричардсона. Однако в этом случае высота барьера не зависит от Wе. Высота барьера теперь зависит от работы выхода коллектора, а также от любых дополнительных приложенных напряжений:[10]

где Wc - работа выхода коллектора с термоэмиссией, ΔVce - приложенное напряжение коллектор-эмиттер; ΔVS это Зеебекское напряжение в горячем эмиттере (влияние ΔVS часто опускается, так как это небольшой вклад порядка 10 мВ). Jc через коллектор (на единицу площади коллектора) снова определяется выражением Закон Ричардсона, кроме сейчас

где А - постоянная типа Ричардсона, которая зависит от материала коллектора, но может также зависеть от материала эмиттера и геометрии диода. В этом случае зависимость Jc на Те, или на ΔVce, может быть приспособлен для получения Wc.

Эта метод замедления потенциала является одним из самых простых и старых методов измерения работы выхода, и он имеет преимущество, поскольку измеряемый материал (коллектор) не требуется, чтобы выдерживать высокие температуры.

Методы, основанные на фотоэмиссии

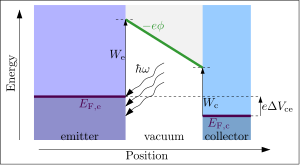
Фотоэлектрический диод в прямое смещение конфигурация, используемая для измерения работы выхода Wе освещенного излучателя.

Фотоэлектрическая работа выхода минимальна. фотон энергия, необходимая для освобождения электрона из вещества, в фотоэлектрический эффект.Если энергия фотона больше работы выхода вещества, фотоэлектрическая эмиссия происходит и электрон высвобождается с поверхности. Подобно описанному выше термоэлектронному случаю, высвободившиеся электроны могут быть извлечены в коллектор и произвести обнаруживаемый ток, если электрическое поле приложено к поверхности эмиттера. В результате возникает избыточная энергия фотонов. в высвободившемся электроне с ненулевой кинетической энергией. ожидается, что минимум энергия фотона требуется, чтобы освободить электрон (и произвести ток),

где Wе - работа выхода эмиттера.

Фотоэлектрические измерения требуют большой осторожности, поскольку неправильно спроектированная экспериментальная геометрия может привести к ошибочному измерению работы выхода.[8] Это может быть причиной большого разброса значений работы выхода в научной литературе. Более того, минимальная энергия может вводить в заблуждение в материалах, в которых нет реальных электронных состояний на уровне Ферми, доступных для возбуждения. Например, в полупроводнике минимальная энергия фотона фактически соответствует валентная полоса край, а не работа выхода.[11]

Конечно, фотоэлектрический эффект можно использовать в замедляющем режиме, как и в описанном выше термоэлектронном устройстве. В случае замедления вместо этого измеряется работа выхода темного коллектора.

Метод зонда Кельвина

Смотрите также: Вольта потенциал, Зондовый силовой микроскоп Кельвина, и Сканирующий зонд Кельвина
Энергетическая диаграмма зонда Кельвина в конфигурации с плоским вакуумом, используемая для измерения разницы работы выхода между образцом и зондом.

Метод зонда Кельвина основан на обнаружении электрического поля (градиент в ϕ) между материалом образца и материалом зонда. электрическое поле можно изменять с помощью напряжения ΔVзр который подается на зонд относительно образца. Если напряжение выбрано таким, что электрическое поле устранено (условие плоского вакуума), то

Поскольку экспериментатор контролирует и знает ΔVзр, то нахождение условия плоского вакуума дает прямую разницу в работе выхода между двумя материалами. Единственный вопрос заключается в том, как определить состояние плоского вакуума? Обычно электрическое поле обнаруживается путем изменения расстояния между образцом и зондом. Когда расстояние меняется, но ΔVзр остается постоянным, ток будет течь из-за изменения емкость. Этот ток пропорционален вакуумному электрическому полю, поэтому, когда электрическое поле нейтрализуется, ток не будет течь.

Хотя метод датчика Кельвина измеряет только разность работы выхода, можно получить абсолютную работу выхода, сначала откалибровав датчик по эталонному материалу (с известной работой выхода), а затем используя тот же датчик для измерения требуемого образца.[9]Технику зонда Кельвина можно использовать для получения карт работы выхода поверхности с чрезвычайно высоким пространственным разрешением, используя острый наконечник зонда (см. Зондовый силовой микроскоп Кельвина ).

Рабочие функции элементов

Работа выхода зависит от конфигурации атомов на поверхности материала. Например, для поликристаллического серебра работа выхода составляет 4,26 эВ, но для кристаллов серебра она изменяется для разных граней кристалла как (100) лицо: 4,64 эВ, (110) лицо: 4,52 эВ, (111) лицо: 4,74 эВ.[12] Диапазоны для типичных поверхностей показаны в таблице ниже.[13]

Работа элементов (эВ )
Ag4.26 – 4.74Al4.06 – 4.26Так как3.75
Au5.10 – 5.47B~4.45Ба2.52 – 2.70
Быть4.98Би4.31C~5
Ca2.87Компакт диск4.08Ce2.9
Co5Cr4.5CS1.95
Cu4.53 – 5.10ЕС2.5Fe:4.67 – 4.81
Ga4.32Б-г2.90Hf3.90
Hg4.475В4.09Ir5.00 – 5.67
K2.29Ла3.5Ли2.9
Лу~3.3Mg3.66Mn4.1
Пн4.36 – 4.95Na2.36Nb3.95 – 4.87
Nd3.2Ni5.04 – 5.35Операционные системы5.93
Pb4.25Pd5.22 – 5.60Pt5.12 – 5.93
Руб.2.261Re4.72Rh4.98
RU4.71Sb4.55 – 4.70Sc3.5
Se5.9Si4.60 – 4.85См2.7
Sn4.42Sr~2.59Та4.00 – 4.80
Tb3.00Te4.95Чт3.4
Ti4.33Tl~3.84U3.63 – 3.90
V4.3W4.32 – 5.22Y3.1
Yb2.60[14]Zn3.63 – 4.9Zr4.05

Физические факторы, определяющие работу выхода

Из-за сложностей, описанных в разделе моделирования ниже, трудно теоретически точно предсказать работу выхода. Однако были выявлены различные тенденции. Работа выхода обычно меньше для металлов с открытой решеткой,[требуется разъяснение ] и больше для металлов, в которых атомы плотно упакованы. На плотных гранях кристалла он несколько выше, чем на открытых, также в зависимости от поверхностные реконструкции для данной грани кристалла.

Поверхностный диполь

Работа выхода не просто зависит от «внутреннего уровня вакуума» внутри материала (т. Е. От его среднего электростатического потенциала) из-за образования атомного масштаба электрический двойной слой на поверхности.[6] Этот поверхностный электрический диполь вызывает скачок электростатического потенциала между материалом и вакуумом.

За поверхностный электрический диполь отвечает множество факторов. Даже с полностью чистой поверхностью электроны могут незначительно распространяться в вакуум, оставляя после себя слегка положительно заряженный слой материала. Это в первую очередь происходит в металлах, где связанные электроны сталкиваются не с потенциалом жесткой стенки на поверхности, а с постепенным нарастанием потенциала из-за плата за изображение Привлечение. Количество поверхностного диполя зависит от детального расположения атомов на поверхности материала, что приводит к изменению работы выхода для разных граней кристалла.

Легирование и влияние электрического поля (полупроводники)

Ленточная диаграмма интерфейса полупроводник-вакуум, показывающий электронное сродство EEA, определяемую как разность энергии приповерхностного вакуума Eпылесос, и приповерхностные зона проводимости край EC. Также показано: Уровень Ферми EF, валентная полоса край EV, рабочая функция W.

В полупроводник, работа выхода чувствительна к уровень допинга на поверхности полупроводника. Поскольку легирование вблизи поверхности также может быть контролируется электрическими полями работа выхода полупроводника также чувствительна к электрическому полю в вакууме.

Причина такой зависимости в том, что обычно уровень вакуума и край зоны проводимости сохраняют фиксированное расстояние независимо от легирования. Этот интервал называется электронное сродство (обратите внимание, что это имеет другое значение, чем сродство к электрону в химии); в кремнии, например, сродство к электрону составляет 4,05 эВ.[15] Если сродство к электрону EEA и зонный уровень Ферми поверхности EF-EC известны, то работа выхода определяется выражением

где EC берется на поверхности.

Исходя из этого, можно было ожидать, что путем легирования основной части полупроводника можно настроить работу выхода. В действительности, однако, энергии зон вблизи поверхности часто привязаны к уровню Ферми из-за влияния поверхностные состояния.[16] Если имеется большая плотность поверхностных состояний, то работа выхода полупроводника будет показывать очень слабую зависимость от легирования или электрического поля.[17]

Теоретические модели работы выхода металла

Теоретическое моделирование работы выхода затруднено, поскольку точная модель требует тщательного рассмотрения как электронных многие эффекты тела и химия поверхности; обе эти темы уже сложны сами по себе.

Одной из первых успешных моделей тенденций работы выхода металла была модель желе модель,[18] которые учитывали колебания электронной плотности вблизи отрывистой поверхности (они похожи на Колебания Фриделя ), а также хвост электронной плотности, выходящий за пределы поверхности. Эта модель показала, почему плотность электронов проводимости (представленная Радиус Вигнера – Зейтца рs) является важным параметром при определении работы выхода.

Модель желе является лишь частичным объяснением, поскольку ее прогнозы все еще показывают значительное отклонение от реальных рабочих функций. Более поздние модели сосредоточены на включении более точных форм обмен электронами и корреляционные эффекты, а также включение зависимости от граней кристалла (для этого необходимо учитывать реальную атомную решетку, что не учитывается в модели желе).[6][19]

использованная литература

  1. ^ Киттель, Чарльз. Введение в физику твердого тела (7-е изд.). Вайли.
  2. ^ Герберт Кремер, "Квазиэлектрические поля и смещения зон: обучение электронов новым трюкам "Нобелевская лекция
  3. ^ "Корреляция и систематика высоты барьера". Acade.brooklyn.cuny.edu. Получено 11 апреля 2018.
  4. ^ Бехунин, Р. О .; Intravaia, F .; Dalvit, D. A. R .; Нето, П. А. М .; Рейно, С. (2012). "Моделирование электростатических пятен в измерениях силы Казимира". Физический обзор A. 85 (1): 012504. arXiv:1108.1761. Bibcode:2012PhRvA..85a2504B. Дои:10.1103 / PhysRevA.85.012504. S2CID  119248753.
  5. ^ Уилл, К. М. (2011). «Наконец, результаты Gravity Probe B». Физика. 4 (43): 43. arXiv:1106.1198. Bibcode:2011PhyOJ ... 4 ... 43 Вт. Дои:10.1103 / Физика.4.43. S2CID  119237335.
  6. ^ а б c «Металлические поверхности 1а». venables.asu.edu. Получено 11 апреля 2018.
  7. ^ Thomas III, S. W .; Велла, С. Дж .; Дики, M.D .; Кауфман, Г. К .; Уайтсайдс, Г. М. (2009). «Управление кинетикой контактной электризации с узорчатыми поверхностями». Журнал Американского химического общества. 131 (25): 8746–8747. CiteSeerX  10.1.1.670.4392. Дои:10.1021 / ja902862b. PMID  19499916.
  8. ^ а б Helander, M. G .; Greiner, M. T .; Wang, Z. B .; Лу, З. Х. (2010). «Подводные камни при измерении работы выхода с помощью фотоэлектронной спектроскопии». Прикладная наука о поверхности. 256 (8): 2602. Bibcode:2010ApSS..256.2602H. Дои:10.1016 / j.apsusc.2009.11.002.
  9. ^ а б Fernández Garrillo, P.A .; Grévin, B .; Chevalier, N .; Боровик, Ł. (2018). «Картирование калиброванной работы выхода с помощью зондовой силовой микроскопии Кельвина». Обзор научных инструментов. 89 (4): 043702. Bibcode:2018RScI ... 89d3702F. Дои:10.1063/1.5007619. PMID  29716375.
  10. ^ Г.Л. Кульцински, "Термоэлектронное преобразование энергии" [1]
  11. ^ «Фотоэлектронная эмиссия». www.virginia.edu. Получено 11 апреля 2018.
  12. ^ Dweydari, A.W .; Ми, К. Х. Б. (1975). «Измерение работы выхода на поверхностях (100) и (110) серебра». Physica Status Solidi A. 27 (1): 223. Bibcode:1975PSSAR..27..223D. Дои:10.1002 / pssa.2210270126.
  13. ^ CRC Handbook of Chemistry and Physics version 2008, p. 12–114.
  14. ^ Николич, М. В .; Radic, S.M .; Миник, В .; Ристич, М. М. (февраль 1996 г.). «Зависимость работы выхода редкоземельных металлов от их электронной структуры». Журнал микроэлектроники. 27 (1): 93–96. Дои:10.1016/0026-2692(95)00097-6. ISSN  0026-2692.
  15. ^ Virginia Semiconductor (июнь 2002 г.). «Общие свойства Si, Ge, SiGe, SiO2 и Si3N4» (PDF). Получено 6 января 2019.
  16. ^ «Свободные поверхности полупроводников». Acade.brooklyn.cuny.edu. Получено 11 апреля 2018.
  17. ^ Бардин, Дж. (1947). «Поверхностные состояния и выпрямление при контакте металлического полупроводника». Физический обзор. 71 (10): 717–727. Bibcode:1947ПхРв ... 71..717Б. Дои:10.1103 / PhysRev.71.717.
  18. ^ Lang, N .; Кон, В. (1971). «Теория металлических поверхностей: работа выхода». Физический обзор B. 3 (4): 1215. Bibcode:1971ПхРвБ ... 3.1215Л. Дои:10.1103 / PhysRevB.3.1215.
  19. ^ Kiejna, A .; Войцеховский, К.Ф. (1996). Электронная физика поверхности металла. Эльзевир. ISBN  9780080536347.

дальнейшее чтение

  • Эшкрофт; Мермин (1976). Физика твердого тела. Thomson Learning, Inc.
  • Гольдштейн, Ньюбери; и другие. (2003). Сканирующая электронная микроскопия и рентгеновский микроанализ. Нью-Йорк: Спрингер.

Для быстрого ознакомления с значениями работы выхода элементов:

внешние ссылки

* Некоторые из рабочих функций, перечисленных на этих сайтах, не согласуются! *