Вычислительная анатомия - Computational anatomy
Эта статья может быть слишком долго читать и удобно ориентироваться. В читаемый размер прозы составляет 113 килобайт. (Ноябрь 2016) |
Вычислительная анатомия это междисциплинарная область биология сосредоточены на количественном исследовании и моделировании изменчивости анатомических форм.[1][2] Она предполагает разработку и применение математических, статистических и аналитических методов моделирования и моделирования биологических структур.
Область широко определена и включает в себя основы в анатомия, Прикладная математика и чистая математика, машинное обучение, вычислительная механика, вычислительная наука, биологическая визуализация, нейробиология, физика, вероятность, и статистика; он также имеет прочные связи с механика жидкости и геометрическая механика. Кроме того, он дополняет новые междисциплинарные области, такие как биоинформатика и нейроинформатика в том смысле, что его интерпретация использует метаданные, полученные из исходных модальностей сенсорной визуализации (из которых Магнитно-резонансная томография это один из примеров). Он фокусируется на анатомических структурах, отображаемых, а не на медицинских устройствах визуализации. По духу она похожа на историю Компьютерная лингвистика, дисциплина, которая фокусируется на лингвистических структурах, а не на датчик действуя как коробка передач и средства массовой информации.
В вычислительной анатомии диффеоморфизм группа используется для изучения различных систем координат с помощью преобразования координат как сгенерировано через Лагранжева и эйлерова скорости потока в . В потоки между координатами в вычислительной анатомии вынуждены быть геодезические потоки удовлетворение принцип наименьшего действия для кинетической энергии потока. Кинетическая энергия определяется через Соболевская гладкость норма со строго более чем двумя обобщенными, интегрируемый с квадратом производные для каждого компонента скорости потока, что гарантирует, что потоки в являются диффеоморфизмами.[3] Это также означает, что импульс диффеоморфной формы взятые поточечно, удовлетворяющие Уравнение Эйлера-Лагранжа для геодезических определяется своими соседями через пространственные производные по полю скорости. Это отделяет дисциплину от случая несжимаемые жидкости[4] для которой импульс поточечно зависит от скорости. Вычислительная анатомия пересекает изучение Римановы многообразия и нелинейный глобальный анализ, где группы диффеоморфизмов являются центральным фокусом. Возникающие многомерные теории формы[5] занимают центральное место во многих исследованиях вычислительной анатомии, как и вопросы, возникающие в молодой области статистика формы.Метрические структуры в вычислительной анатомии по духу связаны с морфометрия, с той разницей, что вычислительная анатомия фокусируется на бесконечномерном пространстве системы координат преобразованный диффеоморфизм, следовательно, центральное использование терминологии диффеоморфометрия, исследование систем координат в метрическом пространстве через диффеоморфизмы.
Бытие
В основе вычислительной анатомии лежит сравнение формы путем распознавания одной формы другой. Это связывает его с Д'Арси Вентворт Томпсон разработки О росте и форме что привело к научному объяснению морфогенез, процесс, с помощью которого узоры сформированы в Биология. Альбрехт Дюрер «Четыре книги о пропорциях человека», возможно, были самыми ранними работами по вычислительной анатомии.[6][7][8] Усилия Ноам Хомский в его новаторстве Компьютерная лингвистика вдохновил на оригинальную формулировку вычислительной анатомии как генеративной модели формы и формы на примерах, на которые воздействовали посредством преобразований.[9]
Благодаря доступности плотных 3D-измерений с помощью таких технологий, как магнитно-резонансная томография (МРТ) вычислительная анатомия возникла как подполе медицинская визуализация и биоинженерия для извлечения анатомических систем координат в масштабе морфома в 3D. Дух этой дисциплины сильно пересекается с такими областями, как компьютерное зрение и кинематика из твердые тела, где объекты исследуются путем анализа группы ответственный за рассматриваемое движение. Вычислительная анатомия отличается от компьютерного зрения с ее фокусом на жестких движениях, поскольку группа бесконечномерных диффеоморфизмов занимает центральное место в анализе биологических форм. Это филиал школы анализа изображений и теории паттернов в Университете Брауна.[10] пионером Ульф Гренандер. В общей метрике Гренандера Теория паттернов, делая пространства узоры в метрическое пространство является одной из фундаментальных операций, поскольку способность группировать и распознавать анатомические конфигурации часто требует метрики близких и отдаленных форм. В метрика диффеоморфометрии[11] Вычислительной анатомии измеряет, насколько далеки друг от друга два диффеоморфных изменения координат, что, в свою очередь, вызывает метрика на формах и изображениях индексируется к ним. Модели теории метрических паттернов,[12][13] в частности, групповые действия на орбите форм и форм являются центральным инструментом формальных определений в вычислительной анатомии.
История
Вычислительная анатомия - это изучение формы и формы на морфома или же общая анатомия миллиметр, или морфология шкалы, ориентируясь на изучение суб-коллекторы из точки, кривые поверхности и подобъемы анатомии человека. Ранним современным компьютерным нейроанатомом был Дэвид Ван Эссен.[14] выполнение некоторых из ранних физических развертываний человеческого мозга, основанных на печати коры головного мозга человека и разрезании. Жан Талаирах публикация Координаты Талаираха является важной вехой в масштабе морфома, демонстрирующей фундаментальную основу локальных систем координат в изучении нейроанатомии и, следовательно, четкую связь с карты дифференциальной геометрии. Одновременно виртуальное отображение в вычислительной анатомии по координатам плотного изображения с высоким разрешением уже происходило в Рузены Байцы[15] и Фреда Букштейна[16] самые ранние разработки на основе Компьютерная аксиальная томография и Магнитно-резонансные изображения.Самое раннее использование потоков диффеоморфизмов для преобразования систем координат в анализе изображений и медицинской визуализации было сделано Кристенсеном, Джоши, Миллером и Рэббиттом.[17][18][19]
Первая формализация вычислительной анатомии в виде орбиты образцовых шаблонов под диффеоморфизм групповое действие был в оригинальной лекции с таким названием, прочитанной Гренандером и Миллером в мае 1997 года на 50-летии отделения прикладной математики в Университете Брауна,[20] и последующая публикация.[9] Это послужило основанием для резкого отхода от большей части предыдущей работы над передовыми методами пространственная нормализация и регистрация изображения которые исторически строились на понятиях дополнения и расширения базиса. Структура, сохраняющая преобразования, центральная в современной области вычислительной анатомии, гомеоморфизмы и диффеоморфизмы гладко переносят гладкие подмногообразия. Они генерируются через Лагранжевы и эйлеровы потоки которые удовлетворяют закону композиции функций, образующих групповое свойство, но не являются аддитивными.
Первоначальная модель вычислительной анатомии была тройной: группа , орбита форм и форм , а вероятностные законы которые кодируют вариации объектов на орбите. Шаблон или набор шаблонов - это элементы на орбите форм.
Лагранжева и гамильтонова формулировки уравнений движения вычислительной анатомии стали известны после 1997 г., когда было проведено несколько ключевых встреч, включая встречу Люмини в 1997 г.[21] организованный Azencott[22] школа в Ecole-Normale Cachan по "Математике распознавания форм" и Триместре 1998 г. Институт Анри Пуанкара é организовано Дэвид Мамфорд "Вопросы математики и традиций сигнала и изображения", которые послужили катализатором для групп Хопкинса-Брауна-ЭНС Кашана, а также последующие разработки и связи вычислительной анатомии с достижениями в глобальном анализе.
Развитие вычислительной анатомии включало установление условий гладкости Собелева на метрике диффеоморфометрии, чтобы гарантировать существование решений вариационный проблемы в пространстве диффеоморфизмов,[23][24] вывод уравнений Эйлера-Лагранжа, характеризующих геодезические, через группу и связанные с ней законы сохранения,[25][26][27] демонстрация метрических свойств правой инвариантной метрики,[28] демонстрация того, что уравнения Эйлера-Лагранжа имеют корректную начальную задачу с единственными решениями на все времена,[29] и с первыми результатами по секционным кривизнам для метрики диффеоморфометрии в пространствах с ориентирами.[30] После встречи в Лос-Аламосе в 2002 г.[31] Джоши[32] оригинальная большая деформация сингулярная Ориентир решения в области вычислительной анатомии были связаны с пиковыми Солитоны или же Пиконы[33] как решения для Камасса-Хольм уравнение. Впоследствии были установлены связи между уравнениями Эйлера-Лагранжа Вычислительной анатомии для плотностей импульса для правоинвариантной метрики, удовлетворяющей гладкости Соболева относительно Владимира Арнольда[4] характеристика Уравнение Эйлера для несжимаемых потоков как описывающие геодезические в группе диффеоморфизмов, сохраняющих объем.[34][35] Первые алгоритмы, обычно называемые LDDMM для диффеоморфного отображения больших деформаций, для вычисления связей между ориентирами в объемах[32][36][37] и сферические коллекторы,[38] кривые,[39] токи и поверхности,[40][41][42] объемы,[43] тензоры,[44] варифолды[45] и временные ряды[46][47][48] последовали.
Этот вклад вычислительной анатомии в глобальный анализ, связанный с бесконечномерными многообразиями подгрупп группы диффеоморфизмов, далеко не тривиален. Первоначальная идея выполнения дифференциальной геометрии, кривизны и геодезических на бесконечномерных многообразиях восходит к Бернхард Риманн с Абилитация (Ueber die Hypothesen, welche der Geometrie zu Grunde liegen[49][50]); Ключевая современная книга, в которой заложены основы таких идей в области глобального анализа, принадлежит Михору.[51]
Приложения в области медицинской визуализации вычислительной анатомии продолжали процветать после двух организованных встреч в Институт чистой и прикладной математики конференции[52][53] в Калифорнийский университет в Лос-Анджелесе. Вычислительная анатомия была полезна для создания точных моделей атрофии человеческого мозга в масштабе морфома, а также сердечных шаблонов,[54] а также при моделировании биологических систем.[55] С конца 1990-х годов вычислительная анатомия стала важной частью разработки новых технологий в области медицинской визуализации. Цифровые атласы являются фундаментальной частью современного медицинского образования.[56][57] и в исследованиях нейровизуализации в масштабе морфома.[58][59] Атласные методы и виртуальные учебники[60] которые учитывают вариации, поскольку деформируемые шаблоны находятся в центре многих платформ анализа нейро-изображений, включая Freesurfer,[61] FSL,[62] MRIStudio,[63] SPM.[64] Диффеоморфная регистрация,[18] представленный в 1990-х годах, в настоящее время является важным игроком с существующими базами кодов, организованными вокруг ANTS,[65] ДАРТЕЛ,[66] ДЕМОНЫ,[67] ЛДДММ,[68] Стационарный ЛДДММ,[69] FastLDDMM,[70] являются примерами активно используемых вычислительных кодов для построения соответствий между системами координат на основе разреженных объектов и плотных изображений. Морфометрия на основе вокселей - важная технология, построенная на многих из этих принципов.
Деформируемая шаблонная орбитальная модель вычислительной анатомии
Модель анатомии человека - это деформируемый шаблон, орбита экземпляров под действием группы. Деформируемые шаблонные модели занимают центральное место в теории метрических шаблонов Гренандера, учитывая типичность с помощью шаблонов и учет изменчивости с помощью преобразования шаблона. Орбита под действием группы как представление деформируемого шаблона - это классическая формулировка из дифференциальной геометрии. Пространство фигур обозначается , с группа с законом состава ; действие группы на фигуры обозначено , где действие группы определено, чтобы удовлетворить
Орбита шаблона становится пространством всех форм, , будучи однородным под действием элементов .
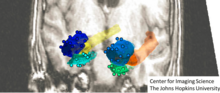
Орбитальная модель вычислительной анатомии - это абстрактная алгебра, которую можно сравнить с линейная алгебра - поскольку группы действуют на фигуры нелинейно. Это обобщение классических моделей линейной алгебры, в которых множество конечномерных векторы заменяются конечномерными анатомическими подмногообразиями (точками, кривыми, поверхностями и объемами) и их изображениями, а матрицы линейной алгебры заменяются преобразованиями координат, основанными на линейных и аффинных группах и более общих многомерных группах диффеоморфизмов.
Формы и формы
Центральные объекты - это формы или формы в вычислительной анатомии, один набор примеров - 0,1,2,3-мерные подмногообразия , второй набор примеров - изображения, созданные с помощью медицинская визуализация например, через магнитно-резонансная томография (МРТ) и функциональная магнитно-резонансная томография.

0-мерные многообразия - это ориентиры или реперные точки; Одномерные многообразия - это кривые, такие как борозды и извилины в мозгу; 2-мерные многообразия соответствуют границам субструктур в анатомии, таких как подкорковые структуры средний мозг или круговая поверхность неокортекс; субобъемы соответствуют подобластям человеческого тела, сердце, то таламус, почка.
вехи представляют собой совокупность точек, не имеющих другой структуры, очерчивающих важные реперные точки в человеческих очертаниях и формах (см. соответствующее изображение с ориентирами).многообразие формы, такие как поверхности представляют собой наборы точек, смоделированных как параметризованные с помощью локальной диаграммы или погружение , (см. рисунок, показывающий формы в виде поверхностей сетки). Изображения, такие как изображения MR или изображения DTI , и - плотные функции являются скалярами, векторами и матрицами (см. рисунок, показывающий скалярное изображение).
Группы и групповые действия

Группы и групповые действия знакомы инженерному сообществу с повсеместной популяризацией и стандартизацией линейная алгебра в качестве базовой модели для анализа сигналы и системы в машиностроение, электротехника и Прикладная математика. В линейной алгебре группы матриц (матрицы с обратными) являются центральной структурой, причем групповое действие определяется обычным определением как матрица, действующая на в качестве векторы; орбита в линейной алгебре - это набор -векторы, заданные , которое является групповым действием матриц через орбиту .
Центральная группа вычислительной анатомии, определенная на объемах в являются диффеоморфизмы которые являются отображениями с 3-компонентными , закон сложения функций , с обратным .
Наиболее популярны скалярные изображения, , с действием справа через инверсию.
- .
Для суб-коллекторы , параметризованный диаграммой или погружение , диффеоморфное действие потока позиции
- .
Несколько групповые действия в вычислительной анатомии были определены.[нужна цитата ]
Лагранжевы и эйлеровы потоки для порождения диффеоморфизмов
Для изучения жесткое тело кинематика, матрица малой размерности Группы Ли были в центре внимания. Матричные группы - это низкоразмерные отображения, которые представляют собой диффеоморфизмы, обеспечивающие взаимно однозначные соответствия между системами координат с гладким обратным. В матричная группа вращений и масштабов могут быть сгенерированы с помощью конечномерных матриц замкнутой формы, которые являются решением простых обыкновенных дифференциальных уравнений с решениями, заданными матричной экспонентой.
Для изучения деформируемой формы в вычислительной анатомии предпочтительной была группа более общих диффеоморфизмов, которая является бесконечномерным аналогом. Группы многомерных диффеоморфизмов, используемые в Computational Anatomy, генерируются с помощью гладких потоков. которые удовлетворяют Лагранжева и эйлерова спецификация полей течения как впервые было введено в.,[17][19][71] удовлетворяющее обыкновенному дифференциальному уравнению:

| (Лагранжев поток) |
с векторные поля на назвал Эйлеров скорость частиц в положении потока. Векторные поля - это функции в функциональном пространстве, моделируемые как гладкие Гильберта пространство большой размерности с якобианом потока поле большой размерности в функциональном пространстве, а не матрица низкой размерности, как в группах матриц. Впервые были представлены потоки[72][73] при больших деформациях при сопоставлении изображений; это мгновенная скорость частицы вовремя .
Обратное требуемая группа определена на векторном поле Эйлера с адвективный обратный поток
| (Обратный транспортный поток) |
Группа диффеоморфизмов вычислительной анатомии
Группа диффеоморфизмов очень большая. Чтобы обеспечить гладкие потоки диффеоморфизмов, избегающие шоковые решения для обратного векторные поля должны быть хотя бы один раз непрерывно дифференцируемыми в пространстве.[74][75] Для диффеоморфизмов на , векторные поля моделируются как элементы гильбертова пространства с использованием Соболев теоремы вложения так, что каждый элемент имеет строго больше двух обобщенных интегрируемых с квадратом пространственных производных (таким образом достаточно), что дает однократные непрерывно дифференцируемые функции.[74][75]
Группа диффеоморфизмов - это потоки с векторными полями, абсолютно интегрируемыми в норме Соболева:
(Группа диффеоморфизмов)
куда с линейным оператором отображение в двойное пространство , интеграл вычисляется интегрированием по частям при является обобщенной функцией в сопряженном пространстве.
Условие соболевской гладкости векторных полей при моделировании в гильбертовом пространстве воспроизводящего ядра
Подход к моделированию, используемый в вычислительной анатомии, обеспечивает выполнение условия непрерывной дифференцируемости векторных полей путем моделирования пространства векторных полей. как воспроизводящее ядро гильбертова пространства (RKHS), с нормой, определенной 1-1, дифференциальным оператором, Обратная Грина . Норма гильбертова пространства индуцирована дифференциальным оператором. За обобщенную функцию или распределение, определите линейную форму как . Это определяет норму на в соответствии с
С является дифференциальным оператором, конечность квадрата нормы включает производные от дифференциального оператора, из которых следует гладкость векторных полей. Вложение Соболева аргументы теоремы были сделаны в[74][75] демонстрируя, что для гладких потоков требуется 1-непрерывная производная. тогда является РХС с оператором назвал Зелень оператор, созданный из Функция Грина (скалярный случай) для случая векторного поля. Ядра Грина, ассоциированные с дифференциальным оператором, гладкие, поскольку ядро непрерывно дифференцируема по обеим переменным, откуда
Когда , векторная плотность, .
Диффеоморфометрия: метрическое пространство форм и форм.
Изучение метрик на группах диффеоморфизмов и изучение метрик между многообразиями и поверхностями было областью значительных исследований.[28][76][77][78][79][80] Метрика диффеоморфометрии измеряет, насколько близко и далеко друг от друга находятся две фигуры или изображения; метрическая длина - это кратчайшая длина потока, который переносит одну систему координат в другую.
Часто знакомая евклидова метрика напрямую не применима, потому что образцы фигур и изображений не образуют векторное пространство. в Риманова орбитальная модель вычислительной анатомии, диффеоморфизмы, действующие на формы не действуйте линейно. Есть много способов определить показатели, и для наборов, связанных с формированием Метрика Хаусдорфа Другой. Метод, который мы используем, чтобы вызвать Риманова метрика используется для создания метрики на орбите форм путем определения ее в терминах длины метрики между преобразованиями диффеоморфной системы координат потоков. Измерение длин геодезического потока между системами координат на орбите фигур называется диффеоморфометрия.
Правоинвариантная метрика на диффеоморфизмах
Определим расстояние на группе диффеоморфизмов
| (метрика-диффеоморфизмы) |
это правоинвариантная метрика диффеоморфометрии,[11][28] инвариантен к изменению параметров пространства, поскольку для всех ,
- .
Метрика форм и форм
Расстояние по формам и формам,[81],
| (метрические формы-формы) |
изображения[28] обозначаются орбитой как и метрическая .
Интеграл действия для принципа Гамильтона на диффеоморфных потоках
В классической механике эволюция физических систем описывается решениями уравнений Эйлера – Лагранжа, связанных с Принцип наименьшего действия из Гамильтон. Это стандартный способ, например получение Законы движения Ньютона свободных частиц. В более общем плане уравнения Эйлера-Лагранжа могут быть выведены для систем обобщенные координаты. Уравнение Эйлера-Лагранжа в вычислительной анатомии описывает геодезические потоки кратчайших путей между системами координат метрики диффеоморфизма. В вычислительной анатомии обобщенные координаты - это поток диффеоморфизма и его лагранжева скорость , эти два связаны через эйлерову скорость . Принцип Гамильтона для генерации уравнения Эйлера-Лагранжа требуется интеграл действия на лагранжиане, задаваемый формулой
(Гамильтониан-интегрированный-лагранжиан)
лагранжиан задается кинетической энергией:
(Лагранжиан-кинетическая энергия)
Диффеоморфный или эйлеровый импульс формы
В вычислительной анатомии сначала был назван Эйлерова или диффеоморфная форма импульса[82] поскольку при интегрировании против эйлеровой скорости дает плотность энергии, и поскольку существует сохранение диффеоморфного импульса формы который имеет место. Оператор является обобщенным момент инерции или инерциальный оператор.
Уравнение Эйлера – Лагранжа об импульсе формы для геодезических на группе диффеоморфизмов
Классический расчет уравнения Эйлера-Лагранжа из Принцип Гамильтона требует возмущения лагранжиана на векторном поле кинетической энергии по отношению к возмущению потока первого порядка. Это требует регулировки Скобка Ли векторного поля, заданный оператором который включает якобиан, заданный формулой
- .
Определение сопряженного то вариация первого порядка дает импульс эйлеровой формы удовлетворяющее обобщенному уравнению:
(EL-General)
значение для всех гладких
Вычислительная анатомия - это изучение движений подмногообразий, точек, кривых, поверхностей и объемов. Импульс, связанный с точками, кривыми и поверхностями, является сингулярным, что подразумевает, что импульс сосредоточен на подмножествах какие измерения в Мера Лебега. В таких случаях энергия все еще хорошо определена. хотя является обобщенной функцией, векторные поля гладкие, а эйлеров импульс понимается через его действие на гладкие функции. Прекрасной иллюстрацией этого является то, что даже когда это суперпозиция дельта-дираков, скорость координат во всем объеме изменяется плавно. Уравнение Эйлера-Лагранжа (EL-General) на диффеоморфизмах обобщенных функций был получен в.[83] В Риманова метрика и скобка Ли для уравнения Эйлера-Лагранжа в геодезических дифференцирования даны в терминах присоединенного оператора и скобки Ли для группы диффеоморфизмов. Его стали называть уравнением EPDiff для диффеоморфизмов, связанных с методом Эйлера-Пуанкаре, после изучения в контексте инерциального оператора для несжимаемых жидкостей без отклонений.[35][84]
Диффеоморфный импульс формы: классическая вектор-функция
Для случая плотности импульса , то уравнение Эйлера – Лагранжа имеет классическое решение:
(EL-Classic)
Уравнение Эйлера-Лагранжа на диффеоморфизмах, классически определенное для плотностей импульса, впервые появилось в[85] для анализа медицинских изображений.
Риманова экспонента (геодезическое позиционирование) и риманов логарифм (геодезические координаты)
В медицинской визуализации и вычислительной анатомии позиционирование и координация форм являются фундаментальными операциями; система позиционирования анатомических координат и форм, построенная на метрике и уравнении Эйлера-Лагранжа; геодезическая система позиционирования, впервые изложенная в работах Миллера Трува и Юнеса.[11]Решение геодезической из начального условия называется Риманово-экспоненциальная, отображение при идентичности к группе.
Риманова экспонента удовлетворяет для начального состояния , динамика векторного поля ,
- для классического уравнения диффеоморфной формы импульса , , тогда
- для обобщенного уравнения, то ,,
Расчет потока на координаты Риманов логарифм,[11][81] отображение при идентичности от в векторное поле ;
Распространены на всю группу, они становятся
; .
Это инверсии друг друга для уникальных решений логарифма; первый называется геодезическое позиционирование, последний геодезические координаты (видеть Экспоненциальное отображение, риманова геометрия для конечномерной версии).Геодезическая метрика является локальным уплощением римановой системы координат (см. рисунок).

Гамильтонова формулировка вычислительной анатомии
В вычислительной анатомии диффеоморфизмы используются для сдвига систем координат, а векторные поля используются в качестве элемента управления внутри анатомической орбиты или морфологического пространства. Модель представляет собой динамическую систему, поток координат и управление векторным полем связанный через Гамильтонов взгляд[81][86][87][88][89] изменяет параметры распределения импульса с точки зрения сопряженный импульс или же канонический импульс, явведен как множитель Лагранжа ограничение лагранжевой скорости .соответственно:
This function is the extended Hamiltonian. В Pontryagin maximum principle[81] gives the optimizing vector field which determines the geodesic flow satisfying as well as the reduced Hamiltonian
The Lagrange multiplier in its action as a linear form has its own inner product of the canonical momentum acting on the velocity of the flow which is dependent on the shape, e.g. for landmarks a sum, for surfaces a surface integral, and. for volumes it is a volume integral with respect to на . In all cases the Greens kernels carry weights which are the canonical momentum evolving according to an ordinary differential equation which corresponds to EL but is the geodesic reparameterization in canonical momentum. The optimizing vector field is given by
with dynamics of canonical momentum reparameterizing the vector field along the geodesic
(Hamiltonian-Dynamics)
Stationarity of the Hamiltonian and kinetic energy along Euler–Lagrange
Whereas the vector fields are extended across the entire background space of , the geodesic flows associated to the submanifolds has Eulerian shape momentum which evolves as a generalized function concentrated to the submanifolds. For landmarks[90][91][92] то geodesics have Eulerian shape momentum which are a superposition of delta distributions travelling with the finite numbers of particles; the diffeomorphic flow of coordinates have velocities in the range of weighted Green's Kernels. For surfaces, the momentum is a surface integral of delta distributions travelling with the surface.[11]
The geodesics connecting coordinate systems satisfying EL-General have stationarity of the Lagrangian. The Hamiltonian is given by the extremum along the path , , равный Lagrangian-Kinetic-Energy and is stationary along EL-General. Defining the geodesic velocity at the identity , then along the geodesic
(Hamiltonian-Geodesics)
The stationarity of the Hamiltonian demonstrates the interpretation of the Lagrange multiplier as momentum; integrated against velocity gives energy density. The canonical momentum has many names. В оптимальный контроль, the flows is interpreted as the state, and is interpreted as conjugate state, or conjugate momentum.[93] The geodesi of EL implies specification of the vector fields or Eulerian momentum в , or specification of canonical momentum determines the flow.
The metric on geodesic flows of landmarks, surfaces, and volumes within the orbit
In computational anatomy the submanifolds are pointsets, curves, surfaces and subvolumes which are the basic primitives. The geodesic flows between the submanifolds determine the distance, and form the basic measuring and transporting tools of диффеоморфометрия. В the geodesic has vector field determined by the conjugate momentum and the Green's kernel of the inertial operator defining the Eulerian momentum . The metric distance between coordinate systems connected via the geodesic determined by the induced distance between identity and group element:
Законы сохранения on diffeomorphic shape momentum for computational anatomy
Given the least-action there is a natural definition of momentum associated to generalized coordinates; the quantity acting against velocity gives energy. The field has studied two forms, the momentum associated to the Eulerian vector field termed Eulerian diffeomorphic shape momentum, and the momentum associated to the initial coordinates or canonical coordinates termed canonical diffeomorphic shape momentum. Each has a conservation law. The conservation of momentum goes hand in hand with the EL-General. In computational anatomy, is the Eulerian Импульс since when integrated against Eulerian velocity gives energy density; оператор the generalized момент инерции or inertial operator which acting on the Eulerian velocity gives momentum which is conserved along the geodesic:
(Euler-Conservation-Constant-Energy)
Conservation of Eulerian shape momentum was shown in[94] and follows from EL-General; conservation of canonical momentum was shown in[81]
The proof follow from defining , подразумевая
The proof on Canonical momentum is shown from :
- .
Geodesic interpolation of information between coordinate systems via variational problems
Construction of diffeomorphic correspondences between shapes calculates the initial vector field coordinates and associated weights on the Greens kernels . These initial coordinates are determined by matching of shapes, called Large Deformation Diffeomorphic Metric Mapping (LDDMM). LDDMM has been solved for landmarks with and without correspondence[32][95][96][97][98] and for dense image matchings.[99][100] кривые,[101] поверхности,[41][102] плотный вектор[103] и тензор[104] изображения и варифолды, меняющие ориентацию.[105] LDDMM calculates geodesic flows of the EL-General onto target coordinates, adding to the action integral an endpoint matching condition measuring the correspondence of elements in the orbit under coordinate system transformation. Existence of solutions were examined for image matching.[24] The solution of the variational problem satisfies the EL-General за with boundary condition.
Matching based on minimizing kinetic energy action with endpoint condition
Conservation from EL-General extends the B.C. в to the rest of the path . The inexact matching problem with the endpoint matching term has several alternative forms. One of the key ideas of the stationarity of the Hamiltonian along the geodesic solution is the integrated running cost reduces to initial cost at t=0, geodesics of the EL-General are determined by their initial condition .
The running cost is reduced to the initial cost determined by из Kernel-Surf.-Land.-Geodesics.
Matching based on geodesic shooting
The matching problem explicitly indexed to initial condition is called shooting, which can also be reparamerized via the conjugate momentum .
Dense image matching in computational anatomy
Dense image matching has a long history now with the earliest efforts[106][107] exploiting a small deformation framework. Large deformations began in the early 1990s,[18][19] with the first existence to solutions to the variational problem for flows of diffeomorphisms for dense image matching established in.[24] Beg solved via one of the earliest LDDMM algorithms based on solving the variational matching with endpoint defined by the dense imagery with respect to the vector fields, taking variations with respect to the vector fields.[99] Another solution for dense image matching reparameterizes the optimization problem in terms of the state giving the solution in terms of the infinitesimal action defined by the адвекция уравнение.[11][27][100]
LDDMM dense image matching
For Beg's LDDMM, denote the Image with group action . Viewing this as an optimal control problem, the state of the system is the diffeomorphic flow of coordinates , with the dynamics relating the control to the state given by . The endpoint matching condition дает вариационную задачу
(Dense-Image-Matching)
Beg's iterative LDDMM algorithm has fixed points which satisfy the necessary optimizer conditions. The iterative algorithm is given in Beg's LDDMM algorithm for dense image matching.
Hamiltonian LDDMM in the reduced advected state
Denote the Image , with state and the dynamics related state and control given by the advective term . The endpoint дает вариационную задачу
(Dense-Image-Matching)
Viallard's iterative Hamiltonian LDDMM has fixed points which satisfy the necessary optimizer conditions.
Diffusion tensor image matching in computational anatomy
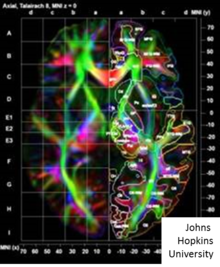
Dense LDDMM tensor matching[104][108] takes the images as 3x1 vectors and 3x3 tensors solving the variational problem matching between coordinate system based on the principle eigenvectors of the diffusion tensor MRI image (DTI) denoted состоящий из -tensor at every voxel. Several of the group actions defined based on the Frobenius матричная норма between square matrices . Shown in the accompanying figure is a DTI image illustrated via its color map depicting the eigenvector orientations of the DTI matrix at each voxel with color determined by the orientation of the directions.Denote the tensor image with eigen-elements , .
Coordinate system transformation based on DTI imaging has exploited two actions one based on the principle eigen-vector or entire matrix.
Согласование LDDMM на основе главного собственного вектора матрицы тензора диффузии создает изображение как единичное векторное поле, определяемое первым собственным вектором. Групповое действие становится
LDDMM matching based on the entire tensor matrixhas group action becomes преобразованные собственные векторы
- .
The variational problem matching onto the principal eigenvector or the matrix is describedLDDMM Tensor Image Matching.
High Angular Resolution Diffusion Image (HARDI) matching in computational anatomy
Диффузионная визуализация с высоким угловым разрешением (HARDI) устраняет хорошо известное ограничение DTI, то есть DTI может выявить только одну доминирующую ориентацию волокна в каждом месте. HARDI измеряет распространение по uniformly distributed directions on the sphere and can characterize more complex fiber geometries. HARDI can be used to reconstruct an orientation distribution function (ODF) that characterizes the angular profile of the diffusion probability density function of water molecules. ODF - это функция, определенная на единичной сфере, .
Dense LDDMM ODF matching [109] takes the HARDI data as ODF at each voxel and solves the LDDMM variational problem in the space of ODF. В области информационная геометрия,[110] the space of ODF forms a Riemannian manifold with the Fisher-Rao metric. For the purpose of LDDMM ODF mapping, the square-root representation is chosen because it is one of the most efficient representations found to date as the various Riemannian operations, such as geodesics, exponential maps, and logarithm maps, are available in closed form. In the following, denote square-root ODF () в качестве , куда неотрицателен для обеспечения уникальности и . The variational problem for matching assumes that two ODF volumes can be generated from one to another via flows of diffeomorphisms , которые являются решениями обыкновенных дифференциальных уравнений starting from the identity map . Denote the action of the diffeomorphism on template as , , are respectively the coordinates of the unit sphere, and the image domain, with the target indexed similarly, ,,.
Групповое действие диффеоморфизма на шаблоне задается согласно
- ,
куда является якобианом аффинно преобразованного ODF и определяется как
This group action of diffeomorphisms on ODF reorients the ODF and reflects changes in both the magnitude of and the sampling directions of due to affine transformation. It guarantees that the volume fraction of fibers oriented toward a small patch must remain the same after the patch is transformed.
Вариационная задача LDDMM определяется как
- .
где логарифм определяется как
куда - нормальное скалярное произведение между точками на сфере под метрика.
Этот алгоритм картирования LDDMM-ODF широко используется для изучения дегенерации белого вещества мозга при старении, болезни Альцгеймера и сосудистой деменции.[111] Атлас белого вещества мозга, созданный на основе ODF, строится с помощью байесовской оценки.[112] Регрессионный анализ ODF разработан в пространстве многообразия ODF в.[113]
Метаморфоза

Основной способ изменения, представленный моделью орбиты, - это изменение координат. Для настройки, при которой пары изображений не связаны диффеоморфизмами, но имеют фотометрические вариации или вариации изображения, не представленные шаблоном, активное моделирование внешности был представлен, первоначально Эдвардс-Кутс-Тейлор[114] и в трехмерной медицинской визуализации в.[115] В контексте вычислительной анатомии, в которой изучались метрики на анатомической орбите, метаморфоза для моделирования структур, таких как опухоли и фотометрических изменений, которые не присутствуют в шаблоне, была введена в[28] для моделей изображений магнитного резонанса, со многими последующими разработками, расширяющими рамки метаморфозы.[116][117][118]
Для сопоставления изображений рамка метаморфозы изображения увеличивает действие так, чтобы с действием . В этом сеттинге метаморфоза сочетает в себе как диффеоморфную трансформацию системы координат вычислительной анатомии, так и ранний морфинг технологии, которые только уменьшали или изменяли фотометрическую или только яркость изображения.
Тогда задача согласования принимает вид с граничными условиями равенства:
Соответствие ориентиров, кривых, поверхностей
Преобразование систем координат на основе Ориентир или же реперный маркер Особенности восходит к ранним работам Bookstein по методам сплайнов малой деформации[119] для интерполяции соответствий, определенных реперными точками, в двухмерное или трехмерное фоновое пространство, в котором определены реперные точки. Методы больших деформаций появились в конце 1990-х годов.[26][32][120] На приведенном выше рисунке изображен ряд ориентиров, связанных с тремя структурами мозга: миндалевидным телом, энторинальной корой и гиппокампом.
Сопоставление геометрических объектов, таких как непомеченные распределения точек, кривые или поверхности, - еще одна распространенная проблема в вычислительной анатомии. Даже в дискретной настройке, где они обычно задаются как вершины с сетками, нет заранее определенных соответствий между точками, в отличие от ситуации ориентиров, описанной выше. С теоретической точки зрения любое подмногообразие в , можно параметризовать в локальных диаграммах , все перепараметризации этих карт геометрически дают одно и то же многообразие. Таким образом, на раннем этапе вычислительной анатомии исследователи определили необходимость параметризации инвариантных представлений. Одним из обязательных требований является то, что термин согласования конечной точки между двумя подмногообразиями сам не зависит от их параметризации. Этого можно достичь с помощью концепций и методов, заимствованных из Геометрическая теория меры, особенно токи[40] и варифолды[45] которые широко использовались для согласования кривых и поверхностей.
Ориентир или точка сопоставления с перепиской


Обозначена обозначенная форма с конечной точкой , вариационная задача принимает вид
- .
(Соответствие ориентира)
Геодезический эйлеров импульс - это обобщенная функция , опираясь на ориентир в вариационной задаче. Условие конечной точки с сохранением подразумевает начальный импульс в единице группы:
Итерационный алгоритм для больших деформаций диффеоморфное метрическое отображение ориентиров дано.
Соответствие меры: незарегистрированные ориентиры
Глон и его сотрудники впервые ввели диффеоморфное сопоставление наборов точек в общую настройку сопоставимых распределений.[121] В отличие от ориентиров, это, в частности, включает ситуацию взвешенных облаков точек без заранее определенных соответствий и, возможно, с разными мощностями. Шаблонное и целевое дискретные облака точек представлены в виде двух взвешенных сумм Дирака. и живя в пространстве подписанные меры из . Пространство снабжено гильбертовой метрикой, полученной из вещественного положительного ядра на , что дает следующую норму:
Затем проблема соответствия между шаблоном и облаком целевых точек может быть сформулирована с использованием этой метрики ядра для термина сопоставления конечных точек:
куда - распределение, переносимое деформацией.
Соответствие кривой
В одномерном случае кривая в 3D может быть представлена вложением , а групповое действие Diff становится . Однако соответствие между кривыми и вложениями не однозначно, как любая репараметризация. , за диффеоморфизм отрезка [0,1] геометрически представляет ту же самую кривую. Чтобы сохранить эту инвариантность в члене согласования конечной точки, можно рассмотреть несколько расширений предыдущего подхода к согласованию 0-мерной меры.
- Согласование кривых с токами
В случае ориентированных кривых токи дают эффективную установку для построения инвариантных членов согласования. В таком представлении кривые интерпретируются как элементы функционального пространства, двойственного векторным полям пространства, и сравниваются через нормы ядра на этих пространствах. Сопоставление двух кривых и в итоге пишет как вариационную задачу
со сроком конечной точки получается из нормы
производная касательный вектор к кривой и заданное матричное ядро . Такие выражения инвариантны к любым положительным перепараметризациям и , и, таким образом, все еще зависят от ориентации двух кривых.
- Сопоставление кривых с помощью варифолдов
Варифолд является альтернативой токам, когда ориентация становится проблемой, например, в ситуациях, связанных с несколькими пучками кривых, для которых невозможно определить «последовательную» ориентацию. Варифолды напрямую расширяют 0-мерные меры, добавляя дополнительное направление касательного пространства к положению точек, что приводит к представлению кривых как мер на произведении и Грассманиан всех прямых в . Тогда проблема соответствия между двумя кривыми состоит в замене члена согласования конечной точки на с варифолдными нормами формы:
куда - неориентированная прямая, направленная касательным вектором и два скалярных ядра соответственно на и грассманиан. Из-за внутренней неориентированной природы грассманова представления такие выражения инвариантны к положительным и отрицательным репараметризациям.
Соответствие поверхности
Сопоставление поверхностей во многом похоже на кривые. Поверхности в параметризуются в локальных диаграммах с помощью вложений , со всеми перепараметризациями с диффеоморфизм U геометрически эквивалентен. Токи и варифолды также можно использовать для формализации согласования поверхностей.
- Согласование поверхностей с токами
Ориентированные поверхности можно представить как 2-токи, двойственные дифференциальным 2-формам. В , можно дополнительно идентифицировать 2-формы с векторными полями через стандартное произведение клина трехмерных векторов. В этом случае сопоставление поверхностей снова записывает:
со сроком конечной точки дано по норме
с вектор нормали к поверхности, параметризованный как .
Этот алгоритм отображения поверхности был проверен для кортикальных поверхностей мозга с помощью CARET и FreeSurfer.[122] Отображение LDDMM для многомасштабных поверхностей обсуждается в.[123]
- Сопоставление поверхностей с помощью варифолдов
Для неориентируемых или неориентируемых поверхностей часто более подходит варифолдный каркас. Определение параметрической поверхности с варифолдом в пространстве мер на произведении и грассманиан, просто заменяется предыдущая текущая метрика к:
куда - (неориентированная) линия, направленная вектором нормали к поверхности.
Рост и атрофия из продольных временных рядов
Есть много настроек, в которых есть серии измерений, временные ряды, которым будут сопоставляться и переходить к лежащим в основе системам координат. Это происходит, например, в моделях динамического роста и атрофии и отслеживании движения, которые были исследованы в[46][124][125][126] Дается наблюдаемая временная последовательность, и цель состоит в том, чтобы вывести временной поток геометрического изменения координат, несущих экземпляры или темплары в течение периода наблюдений.
Общая задача сопоставления временных рядов рассматривает ряд времен как . Поток оптимизируется по ряду затрат предоставление задач оптимизации формы
- .
На данный момент было предложено как минимум три решения: кусочно-геодезические,[46] главная геодезическая[126] и шлицы.[127]
Модель случайной орбиты вычислительной анатомии
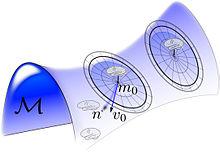
В модель случайной орбиты вычислительной анатомии впервые появилась в[128][129][130] моделирование изменения координат, связанного со случайностью группы, действующей на шаблоны, что вызывает случайность в источнике изображений на анатомической орбите форм и форм и результирующих наблюдений с помощью медицинских устройств визуализации. Такой модель случайной орбиты в котором случайность в группе индуцирует случайность в изображениях, была исследована для специальной евклидовой группы для распознавания объектов в.[131]
На рисунке изображены случайные орбиты вокруг каждого экземпляра, , генерируемый рандомизацией потока путем генерации исходного векторного поля касательного пространства в единице , а затем генерирует случайный объект .
Модель случайной орбиты вызывает априорность форм и изображений. на основе определенного атласа . Для этого генеративная модель генерирует среднее поле как случайное изменение координат шаблона по , где диффеоморфное изменение координат генерируется случайным образом через геодезические потоки. Априор о случайных преобразованиях на индуцируется потоком , с построено как гауссовское случайное поле до . Плотность на случайных наблюдаемых на выходе датчика даны

На рисунке справа изображена мультипликационная орбита - случайный спрей подкорковых многообразий, сгенерированный рандомизацией векторных полей. поддерживается над подмногообразиями.
Байесовская модель вычислительной анатомии

Центральная статистическая модель вычислительной анатомии в контексте медицинская визуализация была моделью канала источника Теория Шеннона;[128][129][130] источник - деформируемый шаблон изображений , выходами каналов являются датчики изображения с наблюдаемыми (см. рисунок).
Видеть Байесовская модель вычислительной анатомии для обсуждений (i) оценка MAP с использованием нескольких атласов, (ii) сегментация MAP с несколькими атласами, оценка шаблонов MAP по популяциям.
Статистическая теория формы в вычислительной анатомии
Форма в вычислительной анатомии - это локальная теория, индексирующая формы и структуры по шаблонам, к которым они биективно нанесен на карту. Статистическая форма в вычислительной анатомии - эмпирическое исследование диффеоморфных соответствий между популяциями и общими шаблонными системами координат. Это сильный отход от Прокруст Анализы и теории формы, впервые разработанные Дэвид Г. Кендалл[132] в том, что центральной группой теорий Кендалла являются конечномерные группы Ли, тогда как теории формы в вычислительной анатомии[133][134][135] сосредоточились на группе диффеоморфизмов, которую до первого порядка через якобиан можно рассматривать как бесконечномерное поле низкоразмерных групп Ли масштабов и вращений.

Модель случайной орбиты обеспечивает естественные условия для понимания эмпирической формы и статистики форм в рамках вычислительной анатомии, поскольку нелинейность индуцированного закона вероятности для анатомических форм и форм индуцируется редукцией к векторным полям в касательном пространстве в единице группы диффеоморфизмов. Последовательный поток уравнения Эйлера порождает случайное пространство форм и форм .
Выполнение эмпирической статистики на этом касательном пространстве в тождестве - естественный способ навести вероятностные законы на статистику формы. Поскольку и векторные поля, и эйлеров импульс находятся в гильбертовом пространстве, естественная модель является одной из гауссовских случайных полей, так что заданная пробная функция , то скалярные произведения с тестовыми функциями распределены по Гауссу со средним значением и ковариацией.
Это изображено на прилагаемом рисунке, где подкорковые структуры мозга изображены в двумерной системе координат, основанной на внутренних продуктах их исходных векторных полей, которые генерируют их из шаблона, показанного в двухмерном пространстве гильбертова пространства.
Оценка шаблона по совокупности
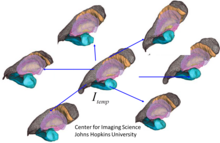
Изучение формы и статистики в популяциях - это локальные теории, индексирующие формы и структуры по шаблонам, которым они сопоставлены биективно. Статистическая форма - это изучение диффеоморфных соответствий относительно шаблона. Ключевой операцией является создание шаблонов из популяций, оценивающих форму, соответствующую совокупности. Существует несколько важных методов создания шаблонов, включая методы, основанные на Frechet усреднение,[137] и статистические подходы, основанные на алгоритм максимизации ожидания и байесовские случайные орбитальные модели вычислительной анатомии.[136][138] На прилагаемом рисунке показана реконструкция подкоркового шаблона из популяции субъектов МРТ.[139]
Программное обеспечение для диффеоморфного отображения
Программные комплексы содержащие множество алгоритмов диффеоморфного отображения, включают следующее:
- Муравьи[65]
- ДАРТЕЛ[66] Морфометрия на основе вокселей
- ДЕФОРМЕТРИКА[140]
- ДЕМОНОВ[67]
- LDDMM[68] Диффеоморфное метрическое отображение большой деформации
- LDDMM на основе ядра на основе кадров [141]
- СтационарныйLDDMM[69]
Облачное программное обеспечение
- MRICloud[142]
Смотрите также
- Байесовская оценка шаблонов в вычислительной анатомии
- Вычислительная нейроанатомия
- Анализ геометрических данных
- Диффеоморфное метрическое отображение большой деформации
- Прокрустовый анализ
- Риманова метрика и скобка Ли в вычислительной анатомии
- Анализ формы (значения)
- Статистический анализ формы
Рекомендации
- ^ «Вычислительная анатомия - Асклепиос». team.inria.fr. Получено 2018-01-01.
- ^ "JHU - Институт вычислительной медицины | Вычислительная анатомия". icm.jhu.edu. Получено 2018-01-01.
- ^ Дюпюи, Поль; Гренандер, Ульф; Миллер, Майкл. "Вариационные задачи о потоках диффеоморфизмов для сопоставления изображений". ResearchGate. Получено 2016-02-20.
- ^ а б Арнольд, В. (1966). "Sur la geomérie différentielle des groups de Lie de Dimension Infinie et ses applications à l'hydrodynamique des fluides parfaits". Анна. Inst. Фурье (На французском). 16 (1): 319–361. Дои:10.5802 / aif.233. МИСТЕР 0202082.
- ^ Лоран Юнес (25 мая 2010 г.). Формы и диффеоморфизмы. Springer. ISBN 9783642120541.
- ^ Дюрер, Альбрехт (1528). Hierinn sind griffen vier Bucher von menschlicher Пропорция durch Albrechten Durer von Nurerberg [sic.] Erfunden und beschuben zu nutz allen denen so zu diser kunst lieb tragen. Иероним Андреа Формшнайдер.
- ^ Библиотека, штат Техас, Центр медицинских наук Техасского университета в Сан-Антонио. "Пропорции человека Альбрехта Дюрера" Библиотека Центра науки здоровья UT ". library.uthscsa.edu. Получено 2016-03-16.
- ^ "Альбрехт Дюрер". Библиотека и музей Моргана. 2014-01-07. Получено 2016-03-16.
- ^ а б Гренандер, Ульф; Миллер, Майкл И. (1998-12-01). «Вычислительная анатомия: новая дисциплина». В. Прил. Математика. 56 (4): 617–694. Дои:10.1090 / qam / 1668732.
- ^ "Университет Брауна - Группа теории паттернов: Главная". www.dam.brown.edu. Получено 2015-12-27.
- ^ а б c d е ж грамм Миллер, Майкл I .; Юнес, Лоран; Труве, Ален (01.03.2014). «Диффеоморфометрия и системы геодезического позиционирования для анатомии человека». Технологии. 2 (1): 36–43. Дои:10.1142 / S2339547814500010. ЧВК 4041578. PMID 24904924.
- ^ Гренандер, Ульф (1993). Общая теория шаблонов: математическое исследование регулярных структур. Издательство Оксфордского университета. ISBN 9780198536710.
- ^ У. Гренандер и М. И. Миллер (2007-02-08). Теория паттернов: от представления к выводу. Оксфорд: Издательство Оксфордского университета. ISBN 9780199297061.
- ^ Van Essen, D.C .; Маунселл, Дж. Х. (1980-05-15). «Двумерные карты коры головного мозга». Журнал сравнительной неврологии. 191 (2): 255–281. Дои:10.1002 / cne.901910208. PMID 7410593. S2CID 25729587.
- ^ Байчи, Рузена; Ковачич, Стане (1 апреля 1989 г.). "Упругое согласование с несколькими разрешениями". Comput. График зрения. Процесс изображения. 46 (1): 1–21. Дои:10.1016 / S0734-189X (89) 80014-3.
- ^ Букштейн, Ф. Л. (1989-06-01). «Основные деформации: тонкопластинчатые шлицы и разложение деформаций». IEEE Trans. Pattern Anal. Мах. Intell. 11 (6): 567–585. Дои:10.1109/34.24792. S2CID 47302.
- ^ а б Кристенсен, Гэри; Рэббит, Ричард; Миллер, Майкл И. (1993-01-01). Джерри Принс (ред.). Учебник деформируемой нейроанатомии на основе механики вязкой жидкости: Труды ... Конференция по информационным наукам и системам. Кафедра электротехники Университета Джонса Хопкинса.
- ^ а б c Christensen, G.E .; Rabbitt, R.D .; Миллер, М. И. (1996-10-01). «Деформируемые шаблоны с использованием кинематики больших деформаций». Пер. Изображение Proc. 5 (10): 1435–1447. Bibcode:1996ITIP .... 5.1435C. Дои:10.1109/83.536892. PMID 18290061.
- ^ а б c Миллер, Майкл; Джоши, Саранг; Кристенсен; Автор книги «Искажение мозга»: Тога, Артур (1997). Деформация мозга: Глава 7: Диффеоморфизмы жидкости большой деформации для сопоставления ориентиров и изображений. п. 115. ISBN 9780080525549.
- ^ Вальтер Фрейбергер (ред.). «Текущие и будущие вызовы в приложениях математики». Квартал прикладной математики.
- ^ "Математический коллок и рекогносцировка форм". www.ceremade.dauphine.fr. Получено 2015-12-19.
- ^ "Роберт Азенкотт, математик-полиглот | La Recherche". www.larecherche.fr. Получено 2016-02-20.
- ^ Труве, Ален. «Подход к распознаванию образов через бесконечномерный диффеоморфизм» (PDF). Архивировано из оригинал (PDF) на 2016-03-04.
- ^ а б c Дюпюи, Поль; Гренандер, Ульф (1998-09-01). "Вариационные задачи о потоках диффеоморфизмов для сопоставления изображений". В. Прил. Математика. LVI (3): 587–600. Дои:10.1090 / qam / 1632326.
- ^ Миллер, Майкл I .; Труве, Ален; Юнес, Лоран (01.01.2002). «О метрике и уравнениях Эйлера-Лагранжа вычислительной анатомии». Ежегодный обзор биомедицинской инженерии. 4: 375–405. CiteSeerX 10.1.1.157.6533. Дои:10.1146 / annurev.bioeng.4.092101.125733. PMID 12117763.
- ^ а б Миллер, Майкл I .; Труве, Ален; Юнес, Лоран (28 января 2006 г.). «Геодезическая съемка для вычислительной анатомии». Журнал математической визуализации и зрения. 24 (2): 209–228. Дои:10.1007 / s10851-005-3624-0. ЧВК 2897162. PMID 20613972.
- ^ а б Миллер, Майкл I .; Труве, Ален; Юнес, Лоран (07.12.2015). "Гамильтоновы системы и оптимальное управление в вычислительной анатомии: 100 лет после Д'Арси Томпсона". Ежегодный обзор биомедицинской инженерии. 17: 447–509. Дои:10.1146 / annurev-bioeng-071114-040601. PMID 26643025.
- ^ а б c d е Miller, M. I .; Юнес, Л. (01.01.2001). «Групповые действия, гомеоморфизмы и сопоставление: общие рамки». Int. J. Comput. Vis. 41 (1–2): 61–84. Дои:10.1023 / А: 1011161132514. S2CID 15423783.
- ^ Trouvé, A .; Юнес, Л. (01.01.2005). «Локальная геометрия деформируемых шаблонов». Журнал SIAM по математическому анализу. 37 (1): 17–59. CiteSeerX 10.1.1.158.302. Дои:10.1137 / S0036141002404838.
- ^ Микели, Марио; Michor, Питер В .; Мамфорд, Дэвид (2012-03-01). «Секционная кривизна в терминах кометрики с приложениями к римановым многообразиям ориентиров». SIAM J. Imaging Sci. 5 (1): 394–433. arXiv:1009.2637. Дои:10.1137 / 10081678X. S2CID 2301243.
- ^ "Домашняя страница". cnls.lanl.gov. Получено 2015-12-19.
- ^ а б c d Joshi, S.C .; Миллер, М. И. (2000-01-01). «Соответствие ориентира через диффеоморфизмы большой деформации». IEEE Transactions по обработке изображений. 9 (8): 1357–1370. Bibcode:2000ITIP .... 9.1357J. Дои:10.1109/83.855431. PMID 18262973. S2CID 6659707.
- ^ Холм, Дэррил Д. (2009-08-29). «Пиконы». В Ж.-П. Франсуаза; Г.Л. Набер; S.T. Цоу (ред.). Энциклопедия математической физики. 4. Оксфорд: Эльзевир. С. 12–20. arXiv:0908.4351. Bibcode:2009arXiv0908.4351H.
- ^ Эбин, Дэвид Дж .; Марсден, Джерролд Э. (1969-09-01). «Группы диффеоморфизмов и решение классических уравнений Эйлера для идеальной жидкости». Бюллетень Американского математического общества. 75 (5): 962–967. Дои:10.1090 / с0002-9904-1969-12315-3.
- ^ а б Мамфорд, Дэвид; Мичор, Питер В. (2013). «Об уравнении Эйлера и EPDiff'". Журнал геометрической механики. 5 (3): 319–344. arXiv:1209.6576. Bibcode:2012arXiv1209.6576M. Дои:10.3934 / jgm.2013.5.319.
- ^ Шерцер, Отмар (23 ноября 2010 г.). Справочник по математическим методам визуализации. Springer Science & Business Media. ISBN 9780387929194.
- ^ Glaunes, J .; Trouve, A .; Юнес, Л. (2004). «Диффеоморфное сопоставление распределений: новый подход к сопоставлению немаркированных наборов точек и подмногообразий». Материалы конференции компьютерного общества IEEE 2004 года по компьютерному зрению и распознаванию образов, 2004 год. CVPR 2004. 2. С. 712–718. CiteSeerX 10.1.1.158.4209. Дои:10.1109 / CVPR.2004.1315234. ISBN 978-0-7695-2158-9.
- ^ Глаунес, Жанна; Vaillant, Marc; Миллер, Майкл I (2004). «Сопоставление ориентиров с помощью диффеоморфизмов большой деформации на сфере: специальный выпуск по математике и анализу изображений». Журнал математической визуализации и зрения. 20: 179–200. Дои:10.1023 / B: JMIV.0000011326.88682.e5. S2CID 21324161. Получено 2016-03-27 - через ResearchGate.
- ^ Ду, Цзя; Юнес, Лоран; Цю, Аньци (01.05.2011). «Диффеоморфное метрическое картирование всего мозга посредством интеграции бороздок и извилин, корковых поверхностей и изображений». NeuroImage. 56 (1): 162–173. Дои:10.1016 / j.neuroimage.2011.01.067. ЧВК 3119076. PMID 21281722.
- ^ а б Vaillant, Marc; Глаунес, Жоан (1 января 2005 г.). «Согласование поверхностей по токам». Обработка информации в медицинской визуализации: материалы ... конференции. Конспект лекций по информатике. 19: 381–392. Дои:10.1007/11505730_32. ISBN 978-3-540-26545-0. PMID 17354711. S2CID 5103312.
- ^ а б Vaillant, Marc; Цю, Аньци; Глаунес, Жанна; Миллер, Майкл И. (2007-02-01). «Диффеоморфное отображение метрической поверхности в верхнем временном круге». NeuroImage. 34 (3): 1149–1159. Дои:10.1016 / j.neuroimage.2006.08.053. ЧВК 3140704. PMID 17185000.
- ^ Дуррлеман, Стэнли; Пеннек, Ксавьер; Труве, Ален; Аяче, Николай (01.10.2009). «Статистические модели множеств кривых и поверхностей на основе токов». Анализ медицинских изображений. 13 (5): 793–808. CiteSeerX 10.1.1.221.5224. Дои:10.1016 / j.media.2009.07.007. PMID 19679507.
- ^ М.Ф. Бег и М. И. Миллер, А. Трув и Л. Юнес (2005). "Вычисление метрических отображений большой деформации через геодезические потоки диффеоморфизмов". Международный журнал компьютерного зрения. 61 (2): 139–157. Дои:10.1023 / B: VISI.0000043755.93987.aa. S2CID 17772076. Получено 2016-01-27 - через ResearchGate.
- ^ Цао, Ян; Миллер, Майкл I .; Мори, Сусуму; Уинслоу, Раймонд Л .; Юнес, Лоран (2006-07-05). «Диффеоморфное сопоставление диффузных тензорных изображений». 2006 Конференция по компьютерному зрению и распознаванию образов Семинар (CVPRW'06). Ход работы. Конференция IEEE Computer Society по компьютерному зрению и распознаванию образов. 2006. п. 67. Дои:10.1109 / CVPRW.2006.65. ISBN 978-0-7695-2646-1. ЧВК 2920614. PMID 20711423.
- ^ а б Харон, Николас; Труве, Ален (2013). «Варифолдное представление неориентированных форм для диффеоморфной регистрации». SIAM Journal on Imaging Sciences. 6 (4): 2547–2580. arXiv:1304.6108. Bibcode:2013arXiv1304.6108C. Дои:10.1137/130918885. S2CID 14335966.
- ^ а б c Миллер, Майкл И. (2004-01-01). «Вычислительная анатомия: сравнение формы, роста и атрофии через диффеоморфизмы». NeuroImage. 23 Дополнение 1: S19–33. CiteSeerX 10.1.1.121.4222. Дои:10.1016 / j.neuroimage.2004.07.021. PMID 15501089. S2CID 13365411.
- ^ Труве, Ален; Виалар, Франсуа-Ксавье (19 марта 2010 г.). "Сплайны форм и стохастические эволюции форм: точка зрения второго порядка". arXiv:1003.3895 [math.OC ].
- ^ Флетчер, П.Т .; Lu, C .; Pizer, S.M .; Джоши, С. (2004-08-01). «Принципиальный геодезический анализ для изучения нелинейной статистики формы». IEEE Transactions по медицинской визуализации. 23 (8): 995–1005. CiteSeerX 10.1.1.76.539. Дои:10.1109 / TMI.2004.831793. PMID 15338733. S2CID 620015.
- ^ "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen". www.maths.tcd.ie. Архивировано из оригинал на 2016-03-18. Получено 2016-03-16.
- ^ Бернхард Риманн. Über die Hypothesen, Welche der Geometrie. Springer. ISBN 9783642351204.
- ^ Питер В. Михор (23 июля 2008 г.). Темы по дифференциальной геометрии. Американское математическое общество. ISBN 9780821820032.
- ^ «Математика в визуализации мозга». NeuroImage. 23 (Приложение 1): S1 – S300. 2004 г.
- ^ Томпсон, Пол М .; Миллер, Майкл I .; Poldrack, Russell A .; Николс, Томас Э .; Тейлор, Джонатан Э .; Уорсли, Кейт Дж .; Ратнанатер, Дж. Тилак (2009). «Математика в визуализации мозга». NeuroImage. 45 (Приложение 1): S1 – S222. Дои:10.1016 / j.neuroimage.2008.10.033. PMID 19027863. S2CID 12143788.
- ^ Fonseca, Carissa G .; Бакхаус, Майкл; Bluemke, David A .; Britten, Randall D .; Чунг, Джэ До; Cowan, Brett R .; Динов, Иво Д .; Финн, Дж. Пол; Хантер, Питер Дж. (2011-08-15). «The Cardiac Atlas Project - база данных изображений для компьютерного моделирования и статистических атласов сердца». Биоинформатика. 27 (16): 2288–2295. Дои:10.1093 / биоинформатика / btr360. ЧВК 3150036. PMID 21737439.
- ^ «Примечания к выпуску CellOrganizer 1.8» (PDF).
- ^ Джейми Вейр; и другие. (2010-03-09). Визуальный атлас анатомии человека (4-е изд.). Эдинбург: Мосби. ISBN 9780723434573.
- ^ "Атлас всего мозга". www.med.harvard.edu. Архивировано из оригинал на 2016-01-18. Получено 2016-01-26.
- ^ Mazziotta, J; Тога, А; Эванс, А; Fox, P; Ланкастер, Дж; Зиллес, К; Вудс, Р. Паус, Т; Симпсон, Г. (2001-08-29). «Вероятностный атлас и справочная система для человеческого мозга: Международный консорциум по картированию мозга (ICBM)». Философские труды Лондонского королевского общества B. 356 (1412): 1293–1322. Дои:10.1098 / rstb.2001.0915. ЧВК 1088516. PMID 11545704.
- ^ "Атлас белого вещества - Атлас диффузионного тензорного изображения трактов белого вещества мозга". www.dtiatlas.org. Получено 2016-01-26.
- ^ Миллер, М. Я; Christensen, G.E .; Амит, Y; Гренандер, У (1993-12-15). «Математический учебник деформируемой нейроанатомии». Труды Национальной академии наук Соединенных Штатов Америки. 90 (24): 11944–11948. Bibcode:1993ПНАС ... 9011944М. Дои:10.1073 / пнас.90.24.11944. ЧВК 48101. PMID 8265653.
- ^ "FreeSurfer". freesurfer.net. Получено 2015-12-08.
- ^ "FSL - FslWiki". fsl.fmrib.ox.ac.uk. Получено 2015-12-08.
- ^ «NITRC: Студия МРТ: Информация об инструментах / ресурсах». www.nitrc.org. Получено 2015-12-08.
- ^ «Программное обеспечение SPM - Статистическое параметрическое отображение». www.fil.ion.ucl.ac.uk. Получено 2015-12-08.
- ^ а б Эшбёрнер, Джон (2007-10-15). «Быстрый алгоритм регистрации диффеоморфных изображений». NeuroImage. 38 (1): 95–113. Дои:10.1016 / j.neuroimage.2007.07.007. PMID 17761438. S2CID 545830.
- ^ а б «Программное обеспечение - Том Веркаутерен». sites.google.com. Получено 2015-12-11.
- ^ а б "NITRC: LDDMM: Информация об инструменте / ресурсе". www.nitrc.org. Получено 2015-12-11.
- ^ а б «Публикация: Сравнение алгоритмов диффеоморфной регистрации: стационарный LDDMM и диффеоморфные демоны». www.openaire.eu. Архивировано из оригинал на 2016-02-16. Получено 2015-12-11.
- ^ Чжан, Мяомяо; Флетчер, П. Томас (01.01.2015). "Конечномерные алгебры Ли для быстрой регистрации диффеоморфных изображений". Обработка информации в медицинской визуализации: материалы ... конференции. Конспект лекций по информатике. 24: 249–259. Дои:10.1007/978-3-319-19992-4_19. ISBN 978-3-319-19991-7. ISSN 1011-2499. PMID 26221678. S2CID 10334673.
- ^ Christensen, G.E .; Rabbitt, R.D .; Миллер, М. И. (1996-10-01). «Деформируемые шаблоны с использованием кинематики больших деформаций». Пер. Изображение Proc. 5 (10): 1435–1447. Bibcode:1996ITIP .... 5.1435C. Дои:10.1109/83.536892. PMID 18290061.
- ^ GE Christensen, RD Rabbitt, MI Miller, Деформируемые шаблоны с использованием кинематики большой деформации, IEEE Trans. Процесс изображения. 1996; 5 (10): 1435-47.
- ^ Г. Е. Кристенсен, С. К. Джоши, М. И. Миллер, Объемная трансформация анатомии головного мозга IEEE Transactions on Medical Imaging, 1997.
- ^ а б c П. Дюпюи, У. Гренандер, М.И. Миллер, Существование решений на потоках диффеоморфизмов, Quarterly of Applied Math, 1997.
- ^ а б c А. Труве. Действие группы бесконечного измерения и разведки в формах. C R Acad Sci Paris Sér I Math, 321 (8): 1031–1034, 1995.
- ^ Юнес, Л. (1998-04-01). «Вычислимые упругие расстояния между формами». Журнал SIAM по прикладной математике. 58 (2): 565–586. CiteSeerX 10.1.1.45.503. Дои:10.1137 / S0036139995287685.
- ^ Мио, Вашингтон; Шривастава, Анудж; Джоши, Шантану (25 сентября 2006 г.). «О форме плоских упругих кривых». Международный журнал компьютерного зрения. 73 (3): 307–324. CiteSeerX 10.1.1.138.2219. Дои:10.1007 / s11263-006-9968-0. S2CID 15202271.
- ^ Michor, Питер В .; Мамфорд, Дэвид; Шах, Джаянт; Юнес, Лоран (2008). «Метрика на пространстве форм с явной геодезией». Ренд. Lincei Mat. Приложение. 9 (2008): 25–57. arXiv:0706.4299. Bibcode:2007arXiv0706.4299M.
- ^ Michor, Питер В .; Мамфорд, Дэвид (2007). «Обзор римановых метрик на пространствах кривых с использованием гамильтонова подхода». Прикладной и вычислительный гармонический анализ. 23 (1): 74–113. arXiv:математика / 0605009. Дои:10.1016 / j.acha.2006.07.004. S2CID 732281.
- ^ Куртек, Себастьян; Классен, Эрик; Гор, Джон С .; Дин, Чжаохуа; Шривастава, Анудж (01.09.2012). «Упругие геодезические пути в пространстве форм параметризованных поверхностей». IEEE Transactions по анализу шаблонов и машинному анализу. 34 (9): 1717–1730. Дои:10.1109 / TPAMI.2011.233. PMID 22144521. S2CID 7178535.
- ^ а б c d е Миллер, Майкл I .; Труве, Ален; Юнес, Лоран (01.01.2015). "Гамильтоновы системы и оптимальное управление в вычислительной анатомии: 100 лет после Д'арси Томпсона". Ежегодный обзор биомедицинской инженерии. 17 (1): 447–509. Дои:10.1146 / annurev-bioeng-071114-040601. PMID 26643025.
- ^ МИЛЛЕР, МАЙКЛ I .; ТРУВЕ, АЛЕН; ЮНС, ЛОРЕН (31.01.2006). «Геодезическая съемка для вычислительной анатомии». Журнал математической визуализации и зрения. 24 (2): 209–228. Дои:10.1007 / s10851-005-3624-0. ЧВК 2897162. PMID 20613972.
- ^ М.И. Миллер, А. Труве, Л. Юнес, Геодезическая съемка в вычислительной анатомии, IJCV, 2006.
- ^ Holm, DD; Marsden, JE; Ратиу, TS (1998). «Уравнения Эйлера-Пуанкаре и полупрямые произведения с приложениями к теориям континуума». Adv. Математика. 137: 1–81. arXiv:chao-dyn / 9801015. Дои:10.1006 / aima.1998.1721. S2CID 163598.
- ^ Miller, M.I .; Trouve, A .; Юнес, L (2002). «О метрике и уравнениях Эйлера-Лагранжа вычислительной анатомии». Анну. Преподобный Биомед. Англ.. 4: 375–405. CiteSeerX 10.1.1.157.6533. Дои:10.1146 / annurev.bioeng.4.092101.125733. PMID 12117763.
- ^ Glaunès J, Trouvé A, Younes L. 2006. Моделирование изменения плоской формы с помощью гамильтоновых потоков кривых. В статистике и анализе форм, под ред. H Krim, A Yezzi Jr, стр. 335–61. Модель. Simul. Sci. Англ. Technol.Boston: Birkhauser
- ^ Микели, Марио; Michor, Питер В .; Мамфорд, Дэвид; Юнес, Лоран (2014). «Анализ деформации формы с точки зрения оптимального управления». arXiv:1401.0661 [math.OC ].
- ^ Миллер, Мичиган; Юнес, L; Труве, А (2014). «Диффеоморфометрия и системы геодезического позиционирования для анатомии человека». Технологии (Singap World Sci). 2: 36–43. Дои:10.1142 / S2339547814500010. ЧВК 4041578. PMID 24904924.
- ^ Michor, Питер В .; Мамфорд, Дэвид (2007-07-01). «Обзор римановых метрик на пространствах кривых с использованием гамильтонова подхода». Прикладной и вычислительный гармонический анализ. Специальный выпуск по математической визуализации. 23 (1): 74–113. arXiv:математика / 0605009. Дои:10.1016 / j.acha.2006.07.004. S2CID 732281.
- ^ Joshi, S .; Миллер, М. (2000). «Соответствие ориентира через диффеоморфизмы большой деформации». IEEE Trans. Процесс изображения. 9 (8): 1357–70. Bibcode:2000ITIP .... 9.1357J. Дои:10.1109/83.855431. PMID 18262973.
- ^ В. Камион, Л. Юнес: геодезические интерполирующие сплайны (EMMCVPR 2001)
- ^ Ж. Глонес, М. Вайан, М. И. Миллер. Сопоставление ориентиров с помощью диффеоморфизмов большой деформации на сфере Journal of Mathematical Imaging and Vision, 2004.
- ^ Миллер, Майкл I .; Труве, Ален; Юнес, Лоран (01.01.2015). "Гамильтоновы системы и оптимальное управление в вычислительной анатомии: 100 лет после Д'Арси Томпсона". Ежегодный обзор биомедицинской инженерии. 17 (1): 447–509. Дои:10.1146 / annurev-bioeng-071114-040601. PMID 26643025.
- ^ МИЛЛЕР, МАЙКЛ I .; ТРУВЕ, АЛЕН; ЮНС, ЛОРЕН (31.01.2006). «Геодезическая съемка для вычислительной анатомии». Журнал математической визуализации и зрения. 24 (2): 209–228. Дои:10.1007 / s10851-005-3624-0. ЧВК 2897162. PMID 20613972.
- ^ Камион, Винсент; Юнес, Лоран (2001-01-01). Геодезические интерполирующие сплайны. Труды Третьего международного семинара по методам минимизации энергии в компьютерном зрении и распознавании образов. EMMCVPR '01. С. 513–527. Дои:10.1007/3-540-44745-8_34. ISBN 978-3-540-42523-6.
- ^ Vaillant, M .; Miller, M. I .; Юнес, Л .; Труве, А. (2004-01-01). «Статистика диффеоморфизмов через представления касательного пространства». NeuroImage. 23 Дополнение 1: S161–169. CiteSeerX 10.1.1.132.6802. Дои:10.1016 / j.neuroimage.2004.07.023. PMID 15501085. S2CID 8255538.
- ^ Марсленд, Стивен; Маклахлан, Роберт (01.01.2007). «Метод гамильтоновых частиц для регистрации диффеоморфных изображений». Обработка информации в медицинской визуализации: материалы ... конференции. Конспект лекций по информатике. 20: 396–407. Дои:10.1007/978-3-540-73273-0_33. ISBN 978-3-540-73272-3. PMID 17633716.
- ^ Glaunes, J; Труве, А; Юнес, L (2004). «Диффеоморфное сопоставление распределений: новый подход к сопоставлению немаркированных точечных множеств и подмногообразий». Л .: Диффеоморфное сопоставление распределений: новый подход к сопоставлению немаркированных точечных множеств и подмногообразий.. ResearchGate. 2. С. 712–718. CiteSeerX 10.1.1.158.4209. Дои:10.1109 / CVPR.2004.1315234. ISBN 978-0-7695-2158-9. Получено 2015-11-25.
- ^ а б Бег, М. Фейсал; Миллер, Майкл I .; Труве, Ален; Юнес, Лоран (01.02.2005). "Вычисление метрических отображений большой деформации с помощью геодезических потоков диффеоморфизмов". Международный журнал компьютерного зрения. 61 (2): 139–157. Дои:10.1023 / B: VISI.0000043755.93987.aa. S2CID 17772076.
- ^ а б Виалар, Франсуа-Ксавье; Рисер, Лоран; Рюкерт, Даниэль; Коттер, Колин Дж. (2012-04-01). «Регистрация диффеоморфных трехмерных изображений с помощью геодезической съемки с использованием эффективного сопряженного расчета». Int. J. Comput. Vis. 97 (2): 229–241. Дои:10.1007 / s11263-011-0481-8. S2CID 18251140.
- ^ Глаунес, Жанна; Цю, Аньци; Миллер, Майкл I .; Юнес, Лоран (2008-12-01). «Отображение диффеоморфной метрической кривой при больших деформациях». Международный журнал компьютерного зрения. 80 (3): 317–336. Дои:10.1007 / s11263-008-0141-9. ЧВК 2858418. PMID 20419045.
- ^ Vaillant, Marc; Глаунес, Жоан (1 января 2005 г.). «Согласование поверхностей по токам». Труды по обработке информации в медицинской визуализации (IPMI 2005), номер 3565 в конспектах лекций по информатике. Конспект лекций по информатике. 19: 381–392. CiteSeerX 10.1.1.88.4666. Дои:10.1007/11505730_32. ISBN 978-3-540-26545-0. PMID 17354711.
- ^ Цао, Ян; Miller, M.I .; Уинслоу, Р.Л .; Юнес, Л. (01.10.2005). Диффеоморфное метрическое отображение ориентаций слоев с большой деформацией. Десятая Международная конференция IEEE по компьютерному зрению, 2005 г. ICCV 2005. 2. С. 1379–1386 Т. 2. CiteSeerX 10.1.1.158.1582. Дои:10.1109 / ICCV.2005.132. ISBN 978-0-7695-2334-7. S2CID 13019795.
- ^ а б Цао, Ян; Miller, M.I .; Уинслоу, Р.Л .; Юнес, Л. (01.09.2005). "Диффеоморфное метрическое отображение больших деформаций векторных полей". IEEE Transactions по медицинской визуализации. 24 (9): 1216–1230. CiteSeerX 10.1.1.157.8377. Дои:10.1109 / TMI.2005.853923. PMID 16156359. S2CID 7046743.
- ^ Charon, N .; Труве, А. (1 января 2013 г.). "Варифолдное представление неориентированных форм для диффеоморфной регистрации". SIAM Journal on Imaging Sciences. 6 (4): 2547–2580. arXiv:1304.6108. Bibcode:2013arXiv1304.6108C. Дои:10.1137/130918885. S2CID 14335966.
- ^ Bajcsy, R .; Lieberson, R .; Райвич, М. (1983-08-01). «Компьютеризированная система для эластичного сопоставления деформированных рентгенографических изображений с идеализированными изображениями атласа». Журнал компьютерной томографии. 7 (4): 618–625. Дои:10.1097/00004728-198308000-00008. PMID 6602820.
- ^ Амит, Яли; Гренандер, Ульф; Пиччони, Мауро (1 июня 1991). «Реставрация структурного изображения с помощью деформируемых шаблонов». Журнал Американской статистической ассоциации. 86 (414): 376–387. Дои:10.1080/01621459.1991.10475053.
- ^ Цао, Ян; Miller, M.I .; Мори, Сусуму; Уинслоу, Р.Л .; Юнес, Л. (01.06.2006). Диффеоморфное сопоставление тензорных изображений диффузии. Конференция по компьютерному зрению и распознаванию образов, 2006. CVPRW '06. 2006. п. 67. Дои:10.1109 / CVPRW.2006.65. ISBN 978-0-7695-2646-1. ЧВК 2920614. PMID 20711423.
- ^ Du, J; Goh, A; Цю, А (2012). «Диффеоморфное метрическое отображение диффузионного изображения с высоким угловым разрешением на основе римановой структуры функций распределения ориентации». IEEE Trans Med Imaging. 31 (5): 1021–1033. Дои:10.1109 / TMI.2011.2178253. PMID 22156979. S2CID 11533837.
- ^ Амари, S (1985). Дифференциально-геометрические методы в статистике. Springer.
- ^ Тонг, JY; Du, J; Ратнараджа, N; Донг, Й; Вскоре HW; Шайни, М; Тан, МЗ; Ta, AT; Чен, К; Цю, А (2014). «Аномалии толщины коры, подкорковых форм и целостности белого вещества при когнитивных нарушениях подкорковых сосудов». Гм. Brain Mapp. 35 (5): 2320–2332. Дои:10.1002 / hbm.22330. ЧВК 6869364. PMID 23861356. S2CID 15230668.
- ^ DU, J; Goh, A; Цю, А (2013). Оценка байесовского атласа по диффузионным изображениям с высоким угловым разрешением (HARDI). Конспект лекций по информатике. 8085. С. 149–157. Дои:10.1007/978-3-642-40020-9_15. ISBN 978-3-642-40019-3. S2CID 8571740.
- ^ Du, J; Goh, A; Кушнарев, С; Цю, А (2014). «Геодезическая регрессия по функциям распределения ориентации с приложением к исследованию старения». NeuroImage. 87: 416–426. Дои:10.1016 / j.neuroimage.2013.06.081. PMID 23851325. S2CID 26942635.
- ^ Cootes, T. F .; Эдвардс, Г. Дж .; Тейлор, К. Дж. (1998-06-02). Буркхардт, Ганс; Нойман, Бернд (ред.). Модели активного внешнего вида. Конспект лекций по информатике. Springer Berlin Heidelberg. С. 484–498. ISBN 9783540646136.
- ^ Лиан, Най-Сян; Давацикос, Христос (01.12.2011). «Морфологические многообразия внешнего вида для группового морфометрического анализа». Анализ медицинских изображений. 15 (6): 814–829. Дои:10.1016 / j.media.2011.06.003. ЧВК 4392008. PMID 21873104.
- ^ Труве, Ален; Юнес, Лоран (01.01.2005). Метаморфозы через действия группы лжи. CiteSeerX 10.1.1.157.8752.
- ^ Холм, Дэррил Д .; Труве, Ален; Юнес, Лоран (2008-06-04). "Теория метаморфозы Эйлера-Пуанкаре". arXiv:0806.0870 [cs.CV ].
- ^ Ричардсон, Кейси Л .; Юнес, Лоран (23 сентября 2014). "Метаморфозы изображений в воспроизводящих гильбертовых пространствах ядра". arXiv:1409.6573 [math.OC ].
- ^ Букштейн, Ф. Л. (1989-01-01). «Основные деформации: тонкопластинчатые шлицы и разложение деформаций» (PDF). IEEE Transactions по анализу шаблонов и машинному анализу. 11 (6): 567–585. Дои:10.1109/34.24792.
- ^ Камион, Винсент; Юнес, Лоран (2001-09-03). Фигейредо, Марио; Зерубия, Джозиан; Джайн, Анил К. (ред.). Геодезические интерполирующие сплайны. Конспект лекций по информатике. Springer Berlin Heidelberg. С. 513–527. CiteSeerX 10.1.1.57.7394. Дои:10.1007/3-540-44745-8_34. ISBN 9783540425236.
- ^ Glaunes, J .; Trouve, A .; Юнес, Л. (2004-06-01). «Диффеоморфное сопоставление распределений: новый подход к сопоставлению немаркированных наборов точек и подмногообразий». Материалы конференции компьютерного общества IEEE 2004 года по компьютерному зрению и распознаванию образов, 2004 год. CVPR 2004. 2. С. II – 712 – II – 718 Том 2. CiteSeerX 10.1.1.158.4209. Дои:10.1109 / CVPR.2004.1315234. ISBN 978-0-7695-2158-9.
- ^ Чжун, Дж; Phua, DY; Цю, А (2010). «Количественная оценка LDDMM, FreeSurfer и CARET для картирования кортикальной поверхности». NeuroImage. 52 (1): 131–141. Дои:10.1016 / j.neuroimage.2010.03.085. PMID 20381626. S2CID 6767322.
- ^ Тан, М; Цю, А (2016). «Диффеоморфное метрическое отображение большой деформации с множественным разрешением для кортикальных поверхностей с множественным разрешением: грубый к точному подходу». IEEE Trans. Процесс изображения. 25 (9): 4061–4074. Bibcode:2016ITIP ... 25.4061T. Дои:10.1109 / TIP.2016.2574982. PMID 27254865. S2CID 16307639.
- ^ Нитхаммер, Марк; Хуанг, Ян; Виалар, Франсуа-Ксавье (01.01.2011). «Геодезическая регрессия для временных рядов изображений». Вычисление медицинских изображений и вмешательство с помощью компьютера: вычислительная анатомия MICI ... Международная конференция по вычислениям медицинских изображений и вмешательству с помощью компьютера. 14 (Pt 2): 655–662. Дои:10.1007/978-3-642-23629-7_80. ЧВК 4339064. PMID 21995085.
- ^ Труве, Ален; Виалар, Франсуа-Ксавье (2010). "Сплайны форм и стохастические эволюции форм: точка зрения второго порядка". arXiv:1003.3895 [math.OC ].
- ^ а б Флетчер, П.Т .; Lu, C .; Pizer, S.M .; Джоши, С. (2004-08-01). «Принципиальный геодезический анализ для изучения нелинейной статистики формы». IEEE Transactions по медицинской визуализации. 23 (8): 995–1005. CiteSeerX 10.1.1.76.539. Дои:10.1109 / TMI.2004.831793. PMID 15338733. S2CID 620015.
- ^ Труве, Ален; Виалар, Франсуа-Ксавье (01.01.2012). «Сплайны формы и стохастическая эволюция формы: точка зрения второго порядка». Квартал прикладной математики. 70 (2): 219–251. arXiv:1003.3895. Дои:10.1090 / S0033-569X-2012-01250-4. S2CID 96421820.
- ^ а б Миллер, Майкл; Банерджи, Аянаншу; Кристенсен, Гэри; Джоши, Саранг; Ханеджа, Навин; Гренандер, Ульф; Матежич, Лариса (01.06.1997). «Статистические методы в вычислительной анатомии». Статистические методы в медицинских исследованиях. 6 (3): 267–299. Дои:10.1177/096228029700600305. PMID 9339500. S2CID 35247542.
- ^ а б У. Гренандер и М. И. Миллер (2007-02-08). Теория паттернов: от представления к выводу. Издательство Оксфордского университета. ISBN 9780199297061.
- ^ а б М. И. Миллер, С. Мори, Х. Тан, Д. Твард и Ю. Чжан (2015-02-14). Байесовские множественные деформируемые шаблоны атласа. Картирование мозга: энциклопедический справочник. Академическая пресса. ISBN 9780123973160.
- ^ Srivastava, S .; Miller, M. I .; Гренандер, У. (1 января 1997 г.). Бирнс, Кристофер I .; Datta, Biswa N .; Мартин, Клайд Ф .; Гиллиам, Дэвид С. (ред.). Эргодические алгоритмы на специальных евклидовых группах для ATR. Системы и управление: основы и приложения. Birkhäuser Boston. С. 327–350. CiteSeerX 10.1.1.44.4751. Дои:10.1007/978-1-4612-4120-1_18. ISBN 978-1-4612-8662-2.
- ^ Кендалл, Дэвид Г. (1989-01-01). «Обзор статистической теории формы». Статистическая наука. 4 (2): 87–99. Дои:10.1214 / сс / 1177012582. JSTOR 2245331.
- ^ Мамфорд, Дэвид (2012-01-01). «Геометрия и кривизна пространств форм». В Zannier, Умберто (ред.). Коллоквиум де Джорджи 2009. Коллоквиумы. Scuola Normale Superiore. С. 43–53. Дои:10.1007/978-88-7642-387-1_4. ISBN 9788876423888. S2CID 116135355.
- ^ Лоран Юнес (25 мая 2010 г.). Формы и диффеоморфизмы (1-е изд.). Springer. ISBN 9783642120541.
- ^ Юнес, Лоран (2012-06-01). «Пространства и многообразия форм в компьютерном зрении: обзор». Image Vision Comput. 30 (6–7): 389–397. Дои:10.1016 / j.imavis.2011.09.009.
- ^ а б Ма, июнь; Миллер, Майкл I .; Younes, Laurent (2010-01-01). "A Bayesian Generative Model for Surface Template Estimation". Международный журнал биомедицинской визуализации. 2010: 1–14. Дои:10.1155/2010/974957. ЧВК 2946602. PMID 20885934.
- ^ Joshi, S .; Davis, Brad; Jomier, B. Matthieu; B, Guido Gerig (2004-01-01). "Unbiased diffeomorphic atlas construction for computational anatomy". NeuroImage. 23: 151–160. CiteSeerX 10.1.1.104.3808. Дои:10.1016/j.neuroimage.2004.07.068. PMID 15501084. S2CID 2271742.
- ^ Ма, июнь; Миллер, Майкл I .; Труве, Ален; Younes, Laurent (2008-08-01). "Bayesian Template Estimation in Computational Anatomy". NeuroImage. 42 (1): 252–261. Дои:10.1016/j.neuroimage.2008.03.056. ЧВК 2602958. PMID 18514544.
- ^ Цю, Аньци; Miller, Michael I. (2008). "Multi-structure network shape analysis via normal surface momentum maps". NeuroImage. 42 (4): 1430–1438. CiteSeerX 10.1.1.463.7231. Дои:10.1016/j.neuroimage.2008.04.257. PMID 18675553. S2CID 10434173.
- ^ "Deformetrica". Получено 12 января 2017.
- ^ Tan, Mingzhen; Qiu, Anqi. "LDDMM with frame-based kernel". Computational Functional Anatomy.
- ^ "MriCloud". Получено 26 октября 2016.







































![phi _ {t}, t in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2152c6909f5234c1dca26e03c6a942cf342275db)

![{ displaystyle v_ {t}, t in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56e95a746da6e27d7a2c9948d7626ebaa9e80893)








![phi _ {t} ^ {- 1}, t in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/87b70d8a52ea026230599e0bc09bcbd18ae00043)

































![{ displaystyle ad_ {v} [w] doteq [v, w] doteq (Dv) w- (Dw) v in V}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64b5f28311579669a18e761f831fc1406657eb8a)

![{ displaystyle { frac {d} {dt}} Av_ {t} + ad_ {v_ {t}} ^ {*} (Av_ {t}) = 0 , t in [0,1] ; }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de0991e07fad09aae70a71defa66440025cf983)







![{ displaystyle { frac {d} {dt}} mu _ {t} + (Dv_ {t}) ^ {T} mu _ {t} + (D mu _ {t}) v_ {t} + ( nabla cdot v) mu _ {t} = 0 , t in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ddc70d6169cce893ff028d45c5dd1ed42d31785)




![{ displaystyle { dot { phi}} _ {t} = v_ {t} circ phi _ {t}, t in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/beecdb7c3dcba90d6b9da06668771f0176aae9a1)

























![t in [0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)










![{ displaystyle { begin {matrix} { text {Eulerian}} & { frac {d} {dt}} int _ {X} Av_ {t} cdot ((D phi _ { t}) w) circ phi _ {t} ^ {- 1}) dx = 0 , t in [0,1]. & { text {Canonical}} & { frac {d} {dt}} int _ {X} p_ {t} cdot ((D phi _ {t}) w) dx = 0 , t в [0,1] { text {для всех}} w in V . end {matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01fcff9002d14951cfcb1e55494bb801acf8ef86)






































![{ displaystyle { dot { phi}} _ {t} = v_ {t} ( phi _ {t}), t in [0,1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22ff70c2574369d841fea1b184176a687d0cf2f6)



























![{ displaystyle displaystyle Av_ {t} in V ^ {*} textstyle, t in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7018f2b4637421e7ac218c4f83307980dc3f88a8)







![{ Displaystyle м: и в [0,1] rightarrow { mathbb {R}} ^ {3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c497295c20c3c6729b5bd80b2f758295a9d081d)












![{ displaystyle | { mathcal {V}} _ {m} | _ {var} ^ {2} = int _ {0} ^ {1} int _ {0} ^ {1} k _ { mathbb {R} ^ {3}} (m (u), m (v)) k _ { mathbf {Gr}} left ([ partial m (u)], [ partial m (v)] right ) {|} partial m (u) {|} {|} partial m (v) {|} , du , dv}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1518a312b8acff68648225aab39b38fbd34c6482)
![{ displaystyle [ partial m (u)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01d8fde9a262eee05f07c1581dbdbf3295ce990d)






![{ displaystyle | { mathcal {V}} _ {m} | _ { mathrm {var}} ^ {2} = iint _ {U times U} k _ { mathbb {R} ^ {3 }} (m (u), m (v)) k _ { mathbf {Gr}} left ([{ vec {n}} (u)], [{ vec {n}} (v)] справа) {|} { vec {n}} (u) {|} {|} { vec {n}} (v) {|} , du , dv}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ad03f859aa1a10c8d2a832a87e0c43714f55325)
![{ Displaystyle [{ vec {п}} (и)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cb7ef8761b7879d7aea6120719fd47e1cac568b)

















