Вечный календарь - Perpetual calendar

Иллюстрация из патента США 248872 1881 года на пресс-папье с вечным календарем. Верхний раздел повернут, чтобы открыть один из семи списков лет (разделение високосных лет), к которым применимы семь календарей ниже.

Карманный календарь на 50 лет, который настраивается поворотом циферблата так, чтобы название месяца помещалось под текущим годом. Затем можно определить день недели или дату.

А вечный календарь это календарь действителен в течение многих лет, обычно предназначен для поиска день недели на заданную дату в будущем.

Для Григорианский и Юлиан календарей, вечный календарь обычно состоит из одного из трех основных вариантов:

14 однолетних календарей плюс таблица, показывающая, какой однолетний календарь следует использовать для каждого года. Эти однолетние календари равномерно делятся на два набора по семь календарей: семь на каждый общий год (год, у которого нет 29 февраля), причем каждый из семи начинается в другой день недели, и семь на каждый високосный год. опять же, каждый из которых начинается в другой день недели, всего четырнадцать. (Видеть Доминическое письмо для одной общей схемы именования для 14 календарей.)
Семь (31-дневный) месячных календарей (или семь каждый из 28–31 дней в месяц, всего 28) и одна или несколько таблиц, чтобы показать, какой календарь используется для любого данного месяца. Таблицы некоторых вечных календарей скользят друг относительно друга, так что выравнивание двух шкал относительно друг друга показывает календарь на конкретный месяц с помощью указателя или механизма окна.^[1] Семь календарей можно объединить в один, либо с 13 столбцами, из которых раскрыты только семь,^[2]^[3] или с подвижными названиями дней недели (как показано на изображении карманного вечного календаря).

Смесь двух вышеперечисленных вариаций - однолетний календарь, в котором названия месяцев фиксированы, а дни недели и даты показаны на подвижных элементах, которые можно менять местами при необходимости.^[4]

В таком вечном календаре не указаны даты подвижные праздники Такие как Пасхальный, которые рассчитываются на основе комбинации событий в Тропический год и лунные циклы. Эти вопросы подробно рассматриваются в Computus.

Один из первых примеров практического использования вечного календаря можно найти в Nürnberger Handschrift GNM 3227a. Календарь охватывает период 1390–1495 гг. (На основании чего рукопись датируется ок. 1389 г.). Для каждого года этого периода в нем указано количество недель между Рождество и Quinquagesima. Это первый известный пример табличной формы вечного календаря, позволяющий рассчитывать подвижные праздники, которые стали популярными в 15 веке.^[5]

Другие варианты использования термина «вечный календарь»

Офисы и торговые точки часто отображают устройства, содержащие набор элементов для формирования всех возможных чисел от 1 до 31, а также названия / сокращения месяцев и дней недели, чтобы показать текущую дату для удобства люди, которые могут подписывать и датировать документы, например чеки. Заведения, которые подают алкогольные напитки, могут использовать вариант, который показывает текущий месяц и день, но вычитает установленный законом возраст употребления алкоголя в годах, указывая самую последнюю официальную дату рождения для покупок алкоголя. Очень простое устройство состоит из два кубика в держателе. Один куб несет числа от нуля до пяти. Другой имеет числа 0, 1, 2, 6 (или 9, если перевернуто), 7 и 8. Это вечно, потому что только один и два могут появиться дважды в дате, и они находятся на обоих кубах.
Определенный календарные реформы были названы вечными календарями, потому что их даты фиксируются в одни и те же дни недели каждый год. Примеры: Мировой Календарь, то Международный фиксированный календарь и Календарь Pax. Технически это не вечные календари, а многолетние календари. Их цель отчасти состоит в том, чтобы исключить необходимость в таблицах, алгоритмах и вычислительных устройствах с вечным календарем.
В часовом производстве термин «вечный календарь» описывает механизм календаря, который правильно отображает дату на часах «постоянно», учитывая различную длину месяцев и високосные годы. Внутренний механизм переведет циферблат на следующий день.^[6]

Алгоритмы

В вечных календарях используются алгоритмы для вычисления дня недели для любого заданного года, месяца и дня месяца. Хотя отдельные операции в формулах могут быть очень эффективно реализованы в программном обеспечении, они слишком сложны для большинства людей, чтобы выполнять все арифметические операции мысленно.^[7] Разработчики вечных календарей скрывают сложность в таблицах, чтобы упростить их использование.

В вечном календаре используется стол чтобы найти, какой из четырнадцати годовых календарей использовать. Таблица для григорианского календаря выражает его 400-летний большой цикл: 303 обычных года и 97 високосных лет в сумме составляют 146 097 дней, или ровно 20 871 неделю. Этот цикл разбивается на один 100-летний период с 25 високосными годами, что составляет 36 525 дней, или один день менее 5218 полных недель; и три 100-летних периода по 24 високосных года, составляющих 36 524 дня, или два дней меньше, чем 5218 полных недель.

В каждом 100-летнем блоке циклический характер григорианского календаря протекает точно так же, как и его юлианский предшественник: обычный год начинается и заканчивается в один и тот же день недели, поэтому следующий год начнется в следующий последующий день. недели. В високосном году есть еще один день, поэтому год, следующий за високосным, начинается с второй день недели после начала високосного года. Каждые четыре года начальный день недели увеличивается на пять дней, поэтому за 28-летний период он увеличивается на 35, возвращаясь на то же место как в прогрессии високосного года, так и в начальный день недели. Этот цикл повторяется трижды за 84 года, оставляя 16 лет в четвертом, неполном цикле века.

Основным осложняющим фактором при построении алгоритма вечного календаря является своеобразная и непостоянная продолжительность февраля, который когда-то был последний месяц года, оставляя первые 11 месяцев с марта по январь с пятимесячным повторяющимся шаблоном: 31, 30, 31, 30, 31, ..., так что смещение с марта начального дня недели для любого месяц можно было легко определить. Конгруэнтность Целлера, известный алгоритм поиска дня недели для любой даты, явно определяет январь и февраль как «13-е» и «14-е» месяцы предыдущий год, чтобы воспользоваться этой регулярностью, но вычисление, зависящее от месяца, все еще очень сложно для ментальной арифметики:

{ displaystyle left lfloor { frac {(m + 1) 26} {10}} right rfloor mod 7,}

Вместо этого вечный календарь на основе таблицы предоставляет простой механизм поиска для определения смещения дня недели для первого дня каждого месяца. Чтобы упростить таблицу, в високосном году январь и февраль должны рассматриваться как отдельный год или иметь дополнительные записи в таблице месяцев:

Месяц	Янв	Фев	Мар	Апр	Май	Июн	Июл	Авг	Сен	Октябрь	Ноя	Декабрь
Добавлять	0	3	3	6	1	4	6	2	5	0	3	5
На високосные годы	6	2	3	6	1	4	6	2	5	0	3	5

Вечный юлианский и григорианский календарь

Таблица первая (cyd)

Контроль результатов показан календарным периодом с 1582 г. до 15 октября возможно, но только для дат по григорианскому календарю.

Подлинно вечный календарь, который позволяет пользователю искать день недели для любой даты по григорианскому календарю.

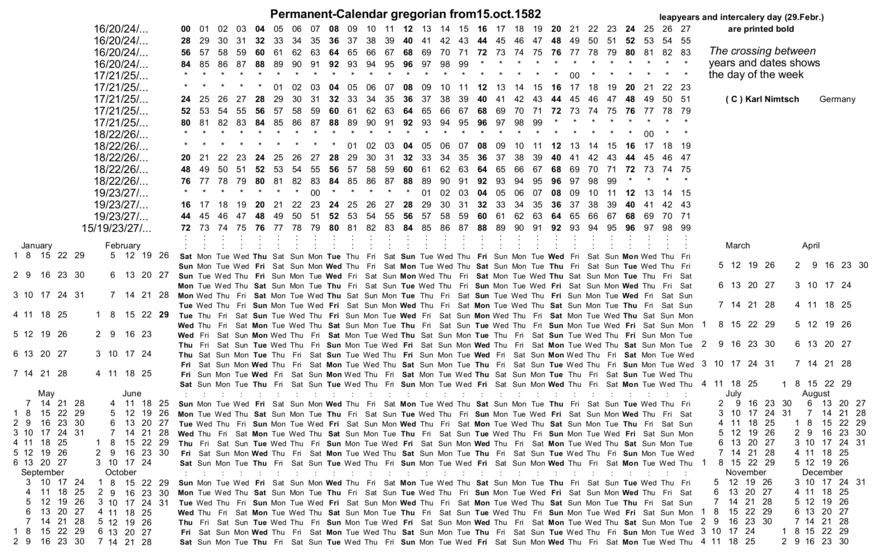
Таблица вторая (cymd)

						Годы века							Пример 1 По н.с. 31 марта 2006 г .:Грег, век 20 (c) и год 06 (y) встречаются в A в таблице Латинский квадрат. Буква A в строке Mar (m) соответствует 31 (d) в пятницу в таблице Будние дни. День пятница. Пример 2 BC 1 января 45:BC 45 = -44 = -100 + 56 (високосный год). -1 и 56 встречаются в B и Янв_B встречается 1 в пт (день). Пример 3 Юлиан 1 января 1900 г .:19 Джулиана встречает 00 в А и Янв_A встречается 1 в субботу (рабочий день). Пример 4 По григорианскому календарю 1 января 1900 г .:Грег 19 встречается с 00 в G, а Jan_G встречается с 1 в понедельник (день).
						00	01	02	03		04	05
						06	07		08	09	10	11
							12	13	14	15		16
						17	18	19		20	21	22
						23		24	25	26	27
						28	29	30	31		32	33
						34	35		36	37	38	39
							40	41	42	43		44
						45	46	47		48	49	50
						51		52	53	54	55
						56	57	58	59		60	61
						62	63		64	65	66	67
							68	69	70	71		72
						73	74	75		76	77	78
						79		80	81	82	83
						84	85	86	87		88	89
						90	91		92	93	94	95
							96	97	98	99
Века						Латинский квадрат								Месяцы
Юлиан				Грег.		Латинский квадрат								Месяцы
-4	3	10	17	—	—	F	E	D	C	B	А	грамм		Янв		Апр	Июл
-3	4	11	18	15	19	грамм	F	E	D	C	B	А		Янв				Октябрь
-2	5	12	19	16	20	А	грамм	F	E	D	C	B				Май
-1	6	13	20	—	—	B	А	грамм	F	E	D	C		Фев			Авг
0	7	14	21	17	21	C	B	А	грамм	F	E	D		Фев	Мар			Ноя
1	8	15	22	—	—	D	C	B	А	грамм	F	E				Июн
2	9	16	23	18	22	E	D	C	B	А	грамм	F					Сен	Декабрь
	Дней					Будние дни
	1	8	15	22	29	Пн	Вт	Мы бы	Чт	Пт	Сидел	солнце
	2	9	16	23	30	Вт	Мы бы	Чт	Пт	Сидел	солнце	Пн
	3	10	17	24	31	Мы бы	Чт	Пт	Сидел	солнце	Пн	Вт
	4	11	18	25		Чт	Пт	Сидел	солнце	Пн	Вт	Мы бы
	5	12	19	26		Пт	Сидел	солнце	Пн	Вт	Мы бы	Чт
	6	13	20	27		Сидел	солнце	Пн	Вт	Мы бы	Чт	Пт
	7	14	21	28		солнце	Пн	Вт	Мы бы	Чт	Пт	Сидел

Юлиан века	Григорианский века	Дни недели							Месяцы					Дней
04 11 18	19 23 27	солнце	Пн	Вт	Мы бы	Чт	Пт	Сидел	Янв	Апри	Июл			01	08	15	22	29
03 10 17		Пн	Вт	Мы бы	Чт	Пт	Сидел	солнце				Сен	Декабрь	02	09	16	23	30
02 09 16	18 22 26	Вт	Мы бы	Чт	Пт	Сидел	солнце	Пн			Июн			03	10	17	24	31
01 08 15		Мы бы	Чт	Пт	Сидел	солнце	Пн	Вт	Фев	Мар			Ноя	04	11	18	25
00 07 14	17 21 25	Чт	Пт	Сидел	солнце	Пн	Вт	Мы бы	Фев			Авг		05	12	19	26
–1 06 13		Пт	Сидел	солнце	Пн	Вт	Мы бы	Чт			Май			06	13	20	27
–2 05 12	16 20 24	Сидел	солнце	Пн	Вт	Мы бы	Чт	Пт	Янв				Октябрь	07	14	21	28

Годы		00	01	02	03		04	05
		06	07		08	09	10	11
			12	13	14	15		16
		17	18	19		20	21	22
		23		24	25	26	27
		28	29	30	31		32	33
		34	35		36	37	38	39
			40	41	42	43		44
		45	46	47		48	49	50
		51		52	53	54	55
		56	57	58	59		60	61
		62	63		64	65	66	67
			68	69	70	71		72
		73	74	75		76	77	78
		79		80	81	82	83
		84	85	86	87		88	89
		90	91		92	93	94	95
			96	97	98	99

Таблица третья (dmyc)

#	Юлиан века (мод 7)	Григорианский века (мод 4)	Даты			01 08 15 22 29	02 09 16 23 30	03 10 17 24 31	04 11 18 25	05 12 19 26	06 13 20 27	07 14 21 28	Годы века (мод 28)
6	05 12 19	16 20 24	Апр	Июл	Янв	солнце	Пн	Вт	Мы бы	Чт	Пт	Сидел	01	07	12	18		29	35	40	46		57	63	68	74		85	91	96
5	06 13 20		Сен	Декабрь		Сидел	солнце	Пн	Вт	Мы бы	Чт	Пт	02		13	19	24	30		41	47	52	58		69	75	80	86		97
4	07 14 21	17 21 25	Июн			Пт	Сидел	солнце	Пн	Вт	Мы бы	Чт	03	08	14		25	31	36	42		53	59	64	70		81	87	92	98
3	08 15 22		Фев	Мар	Ноя	Чт	Пт	Сидел	солнце	Пн	Вт	Мы бы		09	15	20	26		37	43	48	54		65	71	76	82		93	99
2	09 16 23	18 22 26	Авг	Фев		Мы бы	Чт	Пт	Сидел	солнце	Пн	Вт	04	10		21	27	32	38		49	55	60	66		77	83	88	94
1	10 17 24		Май			Вт	Мы бы	Чт	Пт	Сидел	солнце	Пн	05	11	16	22		33	39	44	50		61	67	72	78		89	95
0	11 18 25	19 23 27	Янв	Октябрь		Пн	Вт	Мы бы	Чт	Пт	Сидел	солнце	06		17	23	28	34		45	51	56	62		73	79	84	90		00

Смотрите также

внешняя ссылка

[1] Патент США 1,042,337 , "Календарь (Фред П. Горин)".

[2] Патент США 248872 , "Календарь (Роберт МакКарди)".

[3] «Алюминиевый вечный календарь». 17 сентября 2011 г.

[4] Дёрфлер, Рональд В. (29 августа 2019 г.). "Календарь" графических вычислений "2010". Получено 30 августа 2019.

[5] Трюде Элерт, Райнер Ленг, Frühe Koch- und Pulverrezepte aus der Nürnberger Handschrift GNM 3227a (um 1389); в: Medizin in Geschichte, Philologie und Ethnologie (2003), стр. 291.

[6] «Механизм часов с вечным календарем». 17 сентября 2011 г.

[7] Но см. Формулу в предыдущем разделе, которую очень легко запомнить.

[1]

[2]

[3]

[4]

[5]

[6]

[7]