Теория узлов - Knot theory

Примеры различных узлов, включая тривиальный узел (вверху слева) и трилистник (под этим)

Узловая диаграмма узла-трилистника, простейшего нетривиального узла

В топология, теория узлов это изучение математические узлы. Хотя вдохновленный узлы которые появляются в повседневной жизни, например, в шнурках и веревках, математический узел отличается тем, что концы соединены вместе, так что его нельзя развязать, простейший узел - кольцо (или «развязанный»). На математическом языке узел - это встраивание из круг в 3-х мерном Евклидово пространство, ${ Displaystyle mathbb {R} ^ {3}}$ (в топологии круг не связан с классической геометрической концепцией, но со всеми его гомеоморфизмы ). Два математических узла эквивалентны, если один может быть преобразован в другой посредством деформации ${ Displaystyle mathbb {R} ^ {3}}$ на себя (известный как окружающая изотопия ); эти преобразования соответствуют манипуляциям с завязанной нитью, которые не включают разрезание нити или пропускание нити через себя.

Узлы можно описать по-разному. Однако, учитывая метод описания, может быть более одного описания, которое представляет один и тот же узел. Например, обычным методом описания узла является плоская диаграмма, называемая диаграммой узлов. Любой данный узел можно нарисовать множеством разных способов, используя диаграмму узлов. Следовательно, фундаментальная проблема в теории узлов - определить, когда два описания представляют один и тот же узел.

Существует полное алгоритмическое решение этой проблемы, которое неизвестно. сложность. На практике узлы часто выделяют с помощью инвариант узла, «количество», которое одинаково при вычислении на основе разных описаний узла. Важные инварианты включают узловые многочлены, группы узлов, и гиперболические инварианты.

Первоначальной мотивацией основателей теории узлов было создание таблицы узлов и ссылки, представляющие собой переплетенные друг с другом узлы из нескольких компонентов. Более шести миллиардов узлов и звеньев были сведены в таблицу с начала теории узлов в 19 веке.

Чтобы глубже понять суть, математики обобщили концепцию узла несколькими способами. Узлы можно рассматривать и в других трехмерные пространства и можно использовать объекты, отличные от кругов; увидеть узел (математика). Узлы более высокой размерности п-мерные сферы в м-мерное евклидово пространство.

История

Сложные кельтские узоры в возрасте 1200 лет Келлская книга

Археологи обнаружили, что завязывание узлов восходит к доисторическим временам. Помимо их использования, таких как информация о записи и завязывание объекты вместе, узлы интересовали людей своей эстетикой и духовным символизмом. Узлы появляются в различных формах китайских произведений искусства, датируемых несколькими веками до нашей эры (см. Китайское вязание ). В бесконечный узел появляется в Тибетский буддизм, в то время Кольца Борромео неоднократно появлялись в разных культурах, часто олицетворяя силу в единстве. В кельтский монахи, создавшие Келлская книга расточал целые страницы замысловатыми Кельтское шитье.

Табулятор первого узла, Питер Гатри Тейт

Математическая теория узлов была впервые разработана в 1771 г. Александр-Теофиль Вандермонд которые явно отметили важность топологических особенностей при обсуждении свойств узлов, связанных с геометрией положения. Математические исследования узлов начались в 19 веке с Карл Фридрих Гаусс, который определил связующий интеграл (Серебро 2006 ). В 1860-х годах Лорд Кельвин с теория, что атомы были узлами в эфире привело к Питер Гатри Тейт Создание первых узловых таблиц для полной классификации. Тейт в 1885 году опубликовал таблицу узлов с числом пересечений до десяти, и то, что стало известно как Домыслы Тэйта. Этот отчет мотивировал первых теоретиков узлов, но в конечном итоге теория узлов стала частью возникающей темы топология.

Эти топологи в начале 20 века -Макс Ден, Дж. В. Александер, и др. - изученные узлы с точки зрения группа узлов и инварианты из гомология теория, такая как Полином александра. Это был бы основной подход к теории узлов, пока серия прорывов не изменила предмет.

В конце 1970-х гг. Уильям Терстон представил гиперболическая геометрия в изучение узлов с теорема гиперболизации. Было показано, что многие узлы гиперболические узлы, позволяя использовать геометрию для определения новых мощных инварианты узлов. Открытие Многочлен Джонса от Воан Джонс в 1984 г. (Сосинский 2002, pp. 71–89), и последующие материалы Эдвард Виттен, Максим Концевич и др., выявили глубокую связь между теорией узлов и математическими методами в статистическая механика и квантовая теория поля. С тех пор было изобретено множество инвариантов узлов с использованием сложных инструментов, таких как квантовые группы и Гомология Флоера.

В последние несколько десятилетий ХХ века ученые заинтересовались изучением физические узлы чтобы понять явления завязывания в ДНК и другие полимеры. Теорию узлов можно использовать для определения того, является ли молекула хиральный (имеет "ручность") или нет (Саймон 1986 ). Клубки, струны с обоими концами, закрепленными на месте, эффективно использовались при изучении действия топоизомераза на ДНК (Флапан 2000 ). Теория узлов может сыграть решающую роль в создании квантовых компьютеров через модель топологические квантовые вычисления (Коллинз 2006 ).

Узел эквивалентности

Слева - узелок и эквивалентный ему узел. Может быть сложнее определить, эквивалентны ли сложные узлы, такие как тот, что справа, безузловому.

Узел создается, начиная с одно-размерный отрезок линии, произвольно оборачивая его вокруг себя, а затем соединяя два его свободных конца вместе, чтобы сформировать замкнутый цикл (Адамс 2004 ) (Сосинский 2002 ). Проще говоря, узел ${ displaystyle K}$ является «простой замкнутой кривой» или «(замкнутой) жордановой кривой» (см. Кривая ) - то есть: "почти" инъективный и непрерывная функция ${ Displaystyle К двоеточие [0,1] к mathbb {R} ^ {3}}$, с единственной "неинъективностью" ${ Displaystyle К (0) = К (1)}$. Топологи рассматривают узлы и другие зацепления, такие как ссылки и косы быть эквивалентным, если узел можно плавно толкать, не пересекаясь с самим собой, чтобы он совпал с другим узлом.

Идея узловая эквивалентность состоит в том, чтобы дать точное определение того, когда два узла следует рассматривать как одно и то же, даже если они расположены в пространстве по-разному. Формальное математическое определение таково: два узла ${ displaystyle K_ {1}, K_ {2}}$ эквивалентны, если есть сохраняющий ориентацию гомеоморфизм ${ Displaystyle ч двоеточие mathbb {R} ^ {3} to mathbb {R} ^ {3}}$ с участием ${ displaystyle h (K_ {1}) = K_ {2}}$.

Другой способ определить эквивалентность узлов состоит в том, что два узла эквивалентны, когда существует непрерывное семейство гомеоморфизмов ${ Displaystyle {ч_ {т}: mathbb {R} ^ {3} rightarrow mathbb {R} ^ {3} mathrm {for} 0 leq t leq 1 }}$ пространства на себя, так что последний из них переносит первый узел на второй узел. (Более формально: два узла ${ displaystyle K_ {1}}$ и ${ displaystyle K_ {2}}$ находятся эквивалент если существует непрерывное отображение ${ Displaystyle H: mathbb {R} ^ {3} times [0,1] rightarrow mathbb {R} ^ {3}}$ так что а) для каждого ${ Displaystyle т в [0,1]}$ картографирование ${ Displaystyle х in mathbb {R} ^ {3}}$ к ${ Displaystyle Н (х, т) в mathbb {R} ^ {3}}$ является гомеоморфизмом ${ Displaystyle mathbb {R} ^ {3}}$ на себя; б) ${ Displaystyle Н (х, 0) = х}$ для всех ${ Displaystyle х in mathbb {R} ^ {3}}$; и в) ${ Displaystyle Н (К_ {1}, 1) = К_ {2}}$. Такая функция ${ displaystyle H}$ известен как окружающая изотопия.)

Эти два понятия эквивалентности узлов точно соответствуют тому, какие узлы эквивалентны: два узла, которые эквивалентны при определении сохраняющего ориентацию гомеоморфизма, также эквивалентны при определении объемлющей изотопии, поскольку любые сохраняющие ориентацию гомеоморфизмы ${ Displaystyle mathbb {R} ^ {3}}$ для самого себя является заключительной стадией окружающей изотопии, начиная с идентичности. Наоборот, два узла, эквивалентные по определению объемлющей изотопии, также эквивалентны по определению сохраняющего ориентацию гомеоморфизма, потому что ${ displaystyle t = 1}$ (заключительная) стадия объемлющей изотопии должна быть сохраняющим ориентацию гомеоморфизмом, переносящим один узел на другой.

Основная проблема теории узлов - проблема распознавания, определяет эквивалентность двух узлов. Алгоритмы существуют для решения этой проблемы, с первым из Вольфганг Хакен в конце 1960-х (Хасс 1998 ). Тем не менее, эти алгоритмы могут занимать очень много времени, и основная проблема теории состоит в том, чтобы понять, насколько сложна эта проблема на самом деле (Хасс 1998 ). Частный случай распознавания развязанный, называется проблема распутывания, представляет особый интерес (Хост 2005 ).

Схемы узлов

Полезный способ визуализировать узлы и управлять ими - спроецировать узел на плоскость - представьте себе узел, отбрасывающий тень на стену. Небольшое изменение направления проецирования гарантирует, что один к одному кроме двойных точек, называемых переходы, где «тень» узла пересекает себя один раз в поперечном направлении (Рольфсен 1976 ). При каждом скрещивании, чтобы можно было воссоздать исходный узел, необходимо отличать верхнюю прядь от нижней. Часто это делается путем создания разрыва пряди, идущей снизу. Полученная диаграмма представляет собой кривая погруженной плоскости с дополнительными данными о том, какая нить закончилась, а какая ниже при каждом скрещивании. (Эти диаграммы называются схемы узлов когда они представляют узел и схемы ссылок когда они представляют ссылка на сайт.) Аналогично, узловатые поверхности в 4-пространстве можно связать с погруженные поверхности в 3-м пространстве.

А сокращенная диаграмма диаграмма узлов, в которой нет приводимые переходы (также порочный или съемные переходы), или в котором все приводимые перекрестки удалены. (Weisstein, ReducedKnotDiagram) ошибка harv: несколько целей (2 ×): CITEREFWeisstein (Помогите)(Weisstein, ReducibleCrossing) ошибка harv: несколько целей (2 ×): CITEREFWeisstein (Помогите)

Рейдемейстер движется

В 1927 году, работая с этой схематической формой узлов, Дж. В. Александер и Гарленд Бэрд Бриггс, и независимо Курт Райдемайстер, продемонстрировали, что две диаграммы узлов, принадлежащие одному узлу, могут быть связаны последовательностью трех видов движений на диаграмме, показанной ниже. Эти операции, теперь называемые Рейдемейстер движется, находятся:

Рейдемейстер движется

Тип I	Тип II
Тип III

Доказательство того, что диаграммы эквивалентных узлов связаны движениями Рейдемейстера, основывается на анализе того, что происходит при плоской проекции движения, соединяющего один узел с другим. Движение можно организовать так, чтобы почти всегда проекция была узловой диаграммой, за исключением конечного числа раз, когда происходит «событие» или «катастрофа», например, когда более двух нитей пересекаются в одной точке или несколько нитей. становятся касательными в точке. Внимательное рассмотрение покажет, что сложные события можно исключить, оставив только самые простые события: (1) образование или выпрямление «петли»; (2) две нити, которые касаются в одной точке и проходят сквозь нее; и (3) три нити, пересекающиеся в одной точке. Это в точности ходы Райдемейстера (Сосинский 2002, гл. 3) (Ликориш 1997, гл. 1).

Инварианты узлов

Инвариант узла - это «величина», одинаковая для эквивалентных узлов (Адамс 2004 ) (Lickorish 1997 ) (Рольфсен 1976 ). Например, если инвариант вычисляется из диаграммы узлов, он должен давать одинаковое значение для двух диаграмм узлов, представляющих эквивалентные узлы. Инвариант может принимать одно и то же значение на двух разных узлах, поэтому сам по себе может быть неспособен различить все узлы. Элементарный инвариант трехцветность.

«Классические» инварианты узлов включают группа узлов, какой фундаментальная группа из узел дополнения, а Полином александра, который может быть вычислен из инварианта Александера, модуля, построенного из бесконечного циклического покрытия узлового дополнения (Ликориш 1997 )(Рольфсен 1976 ). В конце 20 века такие инварианты, как "квантовые" полиномы узлов, Инварианты Васильева и были открыты гиперболические инварианты. Эти вышеупомянутые инварианты - лишь верхушка айсберга современной теории узлов.

Узел многочленов

Многочлен узла - это инвариант узла это многочлен. Хорошо известные примеры включают Джонс и Полиномы Александра. Вариант полинома Александера, Полином Александера – Конвея, - многочлен от переменной z с участием целое число коэффициенты (Ликориш 1997 ).

Полином Александера – Конвея фактически определяется в терминах ссылки, которые состоят из одного или нескольких узлов, переплетенных друг с другом. Концепции, описанные выше для узлов, например диаграммы и движения Рейдемейстера, также справедливы для ссылок.

Рассмотрим ориентированную схему ссылок, т.е. тот, в котором каждый компонент ссылки имеет предпочтительное направление, указанное стрелкой. Для данного пересечения диаграммы пусть ${ displaystyle L _ {+}, L _ {-}, L_ {0}}$ быть ориентированными схемами связи, полученными в результате изменения схемы, как показано на рисунке:

Исходная диаграмма может быть либо ${ displaystyle L _ {+}}$ или ${ displaystyle L _ {-}}$, в зависимости от выбранной конфигурации перехода. Тогда многочлен Александера – Конвея, ${ displaystyle C (z)}$, рекурсивно определяется по правилам:

• ${ Displaystyle C (O) = 1}$ (где ${ displaystyle O}$ любая диаграмма развязанный )
• ${ displaystyle C (L _ {+}) = C (L _ {-}) + zC (L_ {0}).}$

Второе правило - это то, что часто называют отношение мотков. Чтобы проверить, что эти правила задают инвариант ориентированного зацепления, следует определить, что многочлен не изменяется при трех движениях Рейдемейстера. Таким образом можно определить многие важные полиномы узлов.

Ниже приводится пример типичного вычисления с использованием отношения мотков. Он вычисляет многочлен Александера – Конвея от трилистник. Желтые участки указывают, где применяется отношение.

C() = C() + z C()

дает развязку и Ссылка Хопфа. Применяя отношение к ссылке Хопфа, где указано,

C() = C() + z C()

дает деформируемое звено с 0 пересечениями (на самом деле это разорвать связь из двух компонентов) и без узла. Разрыв связи требует некоторой хитрости:

C() = C() + z C()

откуда следует, что C(разъединение двух компонентов) = 0, так как первые два многочлена являются несущими и, следовательно, равны.

Сложив все это вместе, вы увидите:

${ Displaystyle С ( mathrm {трилистник}) = 1 + z (0 + z) = 1 + z ^ {2}}$

Поскольку полином Александера – Конвея является инвариантом узла, это показывает, что трилистник не эквивалентен безузлу. Так что трилистник действительно «завязан узлом».

• 

  Левосторонний узел-трилистник.

• 

  Правосторонний узел-трилистник.

Фактически, есть два узла трилистника, называемые правым и левым трилистником, которые зеркальные изображения друг друга (возьмите схему трилистника, приведенную выше, и измените каждое пересечение на другое, чтобы получить зеркальное отображение). Они не эквивалентны друг другу, что означает, что они не амфихиральные. Это было показано Макс Ден, до изобретения многочленов узлов, используя теоретико-групповые методы (Ден 1914 ). Но многочлен Александера – Конвея для каждого вида трилистника будет одинаковым, что можно увидеть, выполнив приведенное выше вычисление с зеркальным отображением. В Джонс полином фактически может различать левый и правый трилистник (Ликориш 1997 ).

Гиперболические инварианты

Уильям Терстон доказано, что многие узлы гиперболические узлы, что означает, что узел дополнения (т. е. множество точек трехмерного пространства не на узле) допускает геометрическую структуру, в частности структуру гиперболическая геометрия. Гиперболическая структура зависит только от узла, поэтому любая величина, вычисленная из гиперболической структуры, является инвариантом узла (Адамс 2004 ).

В Кольца Борромео являются связью со свойством, при котором удаление одного кольца разъединяет другие.

SnapPea вид куспида: Кольца Борромео дополнение с точки зрения обывателя, проживающего рядом с красной составляющей.

Геометрия позволяет нам визуализировать, как выглядит внутренняя часть узла или звена, представляя лучи света движущимися вдоль геодезические геометрии. Примером может служить изображение дополнения к Кольца Борромео. Обитатель этого звена смотрит на пространство рядом с красным компонентом. Шары на картинке - это виды Horoball окрестности ссылки. Путем стандартного утолщения звена получаются горизонтальные окрестности компонент звена. Несмотря на то, что граница окрестности представляет собой тор, если смотреть изнутри дополнения связей, она выглядит как сфера. Каждый компонент связи отображается как бесконечно много сфер (одного цвета), поскольку существует бесконечно много световых лучей от наблюдателя к компоненту связи. Фундаментальный параллелограмм (который показан на рисунке) разбивает плитку как по вертикали, так и по горизонтали и показывает, как бесконечно расширять узор из сфер.

Этот узор, узор «горобол», сам по себе является полезным инвариантом. Другие гиперболические инварианты включают форму основного параллелограмма, длину кратчайшей геодезической и объем. Современные методы табуляции узлов и ссылок эффективно используют эти инварианты. Быстрые компьютеры и умные методы получения этих инвариантов делают вычисление этих инвариантов на практике простой задачей (Адамс, Хильдебранд и Уикс 1991 ).

Высшие измерения

Узел в трех измерениях можно развязать, если поместить его в четырехмерное пространство. Делается это путем смены переходов. Предположим, что одна прядь находится позади другой, если смотреть с выбранной точки. Поднимите его в четвертое измерение, чтобы не было препятствий (передняя прядь не имеет компонентов); затем сдвиньте его вперед и опустите назад, теперь впереди. Аналогия с самолетом - отрыв веревки от поверхности или удаление точки внутри круга.

Фактически, в четырех измерениях любой непересекающийся замкнутый контур одномерной струны эквивалентен узлу. Сначала «протолкните» цикл в трехмерное подпространство, что всегда возможно, хотя и технически объяснимо.

Завязывая сферы высшего измерения

Поскольку узел можно рассматривать топологически как одномерную сферу, следующее обобщение - рассмотрение двумерная сфера (${ Displaystyle mathbb {S} ^ {2}}$), вложенного в 4-мерное евклидово пространство (${ Displaystyle mathbb {R} ^ {4}}$). Такое вложение является узловым, если нет гомеоморфизма ${ Displaystyle mathbb {R} ^ {4}}$ на себя, переводя вложенную 2-сферу в стандартное «круглое» вложение 2-сферы. Подвесные узлы и сплетенные узлы два типичных семейства таких 2-сферных узлов.

Математический метод, называемый «общее положение», подразумевает, что для данного п-сфера в м-мерное евклидово пространство, если м достаточно большой (в зависимости от п) сфера должна быть незаплетенной. В общем, кусочно-линейный н-сферы узелки образовывать только в (п + 2) -мерное пространство (Зееман 1963 ), хотя это больше не требуется для сфер с гладкими узлами. На самом деле есть плавно завязанные (4k - 1) -сферы в 6k-мерное пространство, например есть 3-сфера с гладкими узлами в ${ Displaystyle mathbb {R} ^ {6}}$ (Haefliger 1962 )(Левин 1965 ). Таким образом, коразмерность гладкого узла может быть сколь угодно большой, если не фиксировать размерность завязанной сферы; однако любой гладкий k-сфера встроена в ${ Displaystyle mathbb {R} ^ {п}}$ с 2п − 3k - 3> 0 не завязан. Понятие узла имеет дальнейшие обобщения в математике, см .: узел (математика), изотопическая классификация вложений.

Каждый узел в n-сфера ${ Displaystyle mathbb {S} ^ {п}}$ это ссылка на вещественно-алгебраический набор с изолированной особенностью в ${ Displaystyle mathbb {R} ^ {п + 1}}$ (Акбулут и Кинг 1981 ).

An п-узел - это одиночный ${ Displaystyle mathbb {S} ^ {п}}$ встроенный в ${ Displaystyle mathbb {R} ^ {m}}$. An п-ссылка k-копии ${ Displaystyle mathbb {S} ^ {п}}$ встроенный в ${ Displaystyle mathbb {R} ^ {m}}$, где k натуральное число. Оба м = п + 2 случая и м > п + 2 случая хорошо изучены. п > 1 случай имеет будущее, отличное от п = 1 случай и является захватывающей областью.^[1][2]

Добавление узлов

Добавление двух узлов

Два узла можно добавить, разрезав оба узла и соединив пары концов. Операция называется узловая сумма, или иногда связанная сумма или сочинение двух узлов. Формально это можно определить следующим образом (Адамс 2004 ): рассмотрим плоскую проекцию каждого узла и предположим, что эти проекции не пересекаются. Найдите прямоугольник на плоскости, в котором одна пара противоположных сторон является дугой вдоль каждого узла, а остальная часть прямоугольника не пересекается с узлами. Сформируйте новый узел, удалив первую пару противоположных сторон и соединив другую пару противоположных сторон. Полученный узел представляет собой сумму исходных узлов. В зависимости от того, как это делается, могут образоваться два разных узла (но не более). Эту неоднозначность в сумме можно устранить, рассматривая узлы как ориентированный, т.е. имеющие предпочтительное направление движения вдоль узла и требующие, чтобы дуги узлов в сумме были ориентированы в соответствии с ориентированной границей прямоугольника.

Узловая сумма ориентированных узлов равна коммутативный и ассоциативный. А узел премьер если он нетривиален и не может быть записан как сумма двух нетривиальных узлов. Узел, который можно записать в виде такой суммы, есть составной. Для узлов существует простое разложение, аналогичное премьер и составные числа (Шуберт 1949 ). Для ориентированных узлов это разложение также уникально. Могут быть добавлены и более крупные узлы, но есть некоторые отличия. Хотя вы не можете сформировать узел в трех измерениях, добавив два нетривиальных узла, вы можете в более высоких измерениях, по крайней мере, если учесть гладкий; плавный узлов в коразмерности не менее 3.

Табулирование узлов

Таблица простых узлов до семи пересечений. Узлы помечены обозначениями Александера – Бриггса.

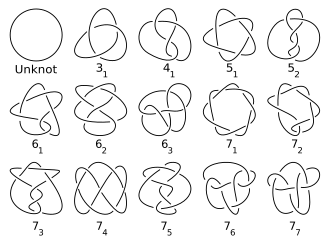
Традиционно сучки каталогизируют по номер перехода. Таблицы узлов обычно включают только простые узлы и только одну запись для узла и его зеркального отображения (даже если они разные) (Hoste, Thistlethwaite & Weeks 1998 ). Количество нетривиальных узлов данного числа пересечений быстро увеличивается, что затрудняет вычисление таблиц (Хост 2005, п. 20). При составлении таблиц удалось насчитать более 6 миллиардов узлов и звеньев (Хост 2005, п. 28). Последовательность количества простых узлов данного номера перекрестка до перекрестка номер 16 равна 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988, 46972, 253293, 1388705... (последовательность A002863 в OEIS ). Хотя экспоненциальные верхняя и нижняя границы для этой последовательности известны, не было доказано, что эта последовательность строго возрастает (Адамс 2004 ).

В первых таблицах узлов Тейта, Литтла и Киркмана использовались узловые диаграммы, хотя Тейт также использовал предшественник Обозначение Даукера. Для узлов были изобретены различные обозначения, которые позволяют более эффективно табулировать (Хост 2005 ).

В ранних таблицах была сделана попытка перечислить все узлы не более чем 10 пересечений и все чередующиеся узлы 11 пересечений (Hoste, Thistlethwaite & Weeks 1998 ). Развитие теории узлов благодаря Александру, Рейдемейстеру, Зейферту и другим облегчило задачу проверки, и таблицы узлов до 9 пересечений включительно были опубликованы Александром-Бриггсом и Рейдемейстером в конце 1920-х годов.

Первая серьезная проверка этой работы была сделана в 1960-х гг. Джон Хортон Конвей, которые не только разработали новую нотацию, но и Полином Александера – Конвея (Конвей 1970 ) (Doll & Hoste 1991 ). Это подтвердило список узлов максимум из 11 переходов и новый список звеньев до 10 переходов. Конвей обнаружил ряд пропусков, но только одно дублирование в таблицах Тейта – Литтла; однако он пропустил дубликаты, называемые Пара перко, что было бы замечено только в 1974 г. Кеннет Перко (Перко 1974 ). Эта известная ошибка распространится, когда Дейл Рольфсен добавил таблицу узлов в свой влиятельный текст, основанный на работе Конвея. Статья Конвея 1970 года по теории узлов также содержит типографское дублирование на его странице с 11 перекрещивающимися узлами без чередования и опускает 4 примера - 2 ранее перечисленных в старшей диссертации Д. Ломбардеро в Принстоне 1968 года и еще 2, обнаруженные впоследствии Ален Кодрон. [см. Перко (1982), Примитивность некоторых узлов, Труды по топологии] Менее известен дубликат в его таблице 10 перекрестных связей: 2.-2.-20.20 является зеркалом 8 * -20: -20. [См. Perko (2016), Исторические моменты нециклической теории узлов, J. Разветвления теории узлов].

В конце 1990-х Хост, Тистлтуэйт и Уикс подсчитали все узлы через 16 пересечений (Hoste, Thistlethwaite & Weeks 1998 ). В 2003 году Ранкин, Флинт и Шерманн составили таблицу чередующиеся узлы через 22 перехода (Хост 2005 ).

Обозначения Александра – Бриггса

Это наиболее традиционные обозначения из-за статьи 1927 г. Джеймс В. Александр и Гарланд Б. Бриггс и позже продлен Дейл Рольфсен в его таблице узлов (см. изображение выше и Список простых узлов ). Обозначения просто упорядочивают узлы по их числу пересечений. Один записывает номер пересечения с нижним индексом, чтобы обозначить его порядок среди всех узлов с этим номером пересечения. Этот порядок произвольный и поэтому не имеет особого значения (хотя в каждом количестве пересечений завязать узел приходит после торический узел ). Ссылки записываются номером пересечения с верхним индексом для обозначения количества компонентов и нижним индексом для обозначения его порядка в ссылках с одинаковым количеством компонентов и пересечений. Таким образом, узел трилистника обозначается 3₁ а ссылка Хопфа - 2²
₁. Имена Александра – Бриггса в диапазоне 10₁₆₂ до 10₁₆₆ неоднозначны из-за открытия Пара перко в Чарльз Ньютон Литтл исходная и последующие таблицы узлов, а также различия в подходах к исправлению этой ошибки в таблицах узлов и других публикациях, созданных после этого момента.^[3]

Обозначение Даукера – Тистлтуэйта

Узловая диаграмма с пересечениями, помеченными для последовательности Даукера

В Обозначение Даукера – Тистлтуэйта, также называемый нотацией или кодом Даукера, поскольку узел - это конечная последовательность четных целых чисел. Числа генерируются, следуя за узлом и отмечая перекрестки последовательными целыми числами. Поскольку каждый перекресток посещается дважды, это создает пару четных целых чисел с нечетными целыми числами. Соответствующий знак указывает на пересечение и пересечение. Например, на этом рисунке узловая диаграмма имеет пересечения, помеченные парами (1,6) (3, −12) (5,2) (7,8) (9, −4) и (11, −10). Обозначение Даукера – Тистлтуэйта для этой маркировки - это последовательность: 6, −12, 2, 8, −4, −10. Узловая диаграмма имеет более одной возможной нотации Даукера, и существует хорошо понятная неоднозначность при восстановлении узла из нотации Даукера – Тислтуэйта.

Обозначение Конвея

В Обозначение Конвея для узлов и звеньев им. Джон Хортон Конвей, основан на теории путаница (Конвей 1970 ). Преимущество этого обозначения в том, что оно отражает некоторые свойства узла или звена.

Обозначения описывает, как построить конкретную диаграмму ссылок для ссылки. Начните с основной многогранник, 4-валентный связный плоский граф без Digon регионы. Такой многогранник сначала обозначается числом вершин, а затем числом звездочек, которые определяют положение многогранника в списке основных многогранников. Например, 10 ** обозначает второй многогранник с 10 вершинами в списке Конвея.

Тогда каждая вершина имеет алгебраический клубок подставляется в него (каждая вершина ориентирована, поэтому произвольный выбор для замены отсутствует). Каждый такой клубок имеет обозначение, состоящее из чисел и знаков + или -.

Пример: 1 * 2 −3 2. 1 * обозначает единственный базовый многогранник с 1 вершиной. 2 −3 2 - это последовательность, описывающая непрерывную дробь, связанную с рациональный клубок. Вставляем этот клубок в вершину основного многогранника 1 *.

Более сложный пример: 8 * 3.1.2 0.1.1.1.1.1 Здесь снова 8 * относится к базовому многограннику с 8 вершинами. Точки разделяют обозначения для каждого клубка.

Любая ссылка допускает такое описание, и ясно, что это очень компактное обозначение даже для очень большого числа перекрестков. Обычно используются еще несколько сокращений. Последний пример обычно пишется 8 * 3: 2 0, где единицы опускаются и сохраняется количество точек, за исключением точек в конце. Для алгебраического узла, такого как в первом примере, 1 * часто опускается.

В новаторской статье Конвея по этой теме перечислено до 10-вершинных базовых многогранников, которые он использует для табулирования связей, которые стали стандартом для этих связей. Для дальнейшего перечисления многогранников с высшими вершинами доступны нестандартные варианты.

Код Гаусса

Код Гаусса подобно нотации Доукера – Тистлтуэйта, представляет собой узел с последовательностью целых чисел. Однако вместо того, чтобы обозначать каждый перекресток двумя разными номерами, перекрестки обозначаются только одним номером. Когда переход является переходом, отображается положительное число. В андеркроссинге отрицательное число. Например, узел трилистника в коде Гаусса может быть задан как: 1, −2,3, −1,2, −3

Код Гаусса ограничен в своей способности идентифицировать узлы. Эта проблема частично решается с помощью расширенный код Гаусса.

Смотрите также

• Контактная геометрия # Лежандровые подмногообразия и узлы
• Узлы и графики
• Список тем теории узлов
• Молекулярный узел
• Квантовые узлы
• Квантовая топология
• Топология схемы
• Теория ленты
• Галстук § Виды узла

использованная литература

• Адамс, Колин (2004), Книга узлов: элементарное введение в математическую теорию узлов, Американское математическое общество, ISBN  978-0-8218-3678-1
• Адамс, Колин; Хильдебранд, Мартин; Недели, Джеффри (1991), "Гиперболические инварианты узлов и зацеплений", Труды Американского математического общества, 326 (1): 1–56, Дои:10.1090 / s0002-9947-1991-0994161-2, JSTOR  2001854
• Акбулут, Сельман; Кинг, Генри К. (1981), «Все узлы алгебраические», Comm. Математика. Helv., 56 (3): 339–351, Дои:10.1007 / BF02566217
• Бар-Натан, Дрор (1995), "Об инвариантах узла Васильева", Топология, 34 (2): 423–472, Дои:10.1016/0040-9383(95)93237-2
• Коллинз, Грэм (апрель 2006 г.), «Вычисления с квантовыми узлами», Scientific American, 294 (4), стр. 56–63, Bibcode:2006SciAm.294d..56C, Дои:10.1038 / scientificamerican0406-56
• Ден, Макс (1914), "Die beiden Kleeblattschlingen", Mathematische Annalen, 75: 402–413
• Конвей, Джон Хортон (1970), «Перечисление узлов и зацеплений и некоторые их алгебраические свойства», Вычислительные задачи абстрактной алгебры, Пергамон, стр. 329–358, ISBN  978-0080129754, OCLC  322649
• Кукла, Гельмут; Хост, Джим (1991), "Таблица ориентированных ссылок. С приложением микрофиши", Математика. Комп., 57 (196): 747–761, Bibcode:1991MaCom..57..747D, Дои:10.1090 / S0025-5718-1991-1094946-4
• Флапан, Эрика (2000), Когда топология встречается с химией: топологический взгляд на хиральность молекул, Outlook, Издательство Кембриджского университета, ISBN  978-0-521-66254-3
• Хефлигер, Андре (1962), "Завязанный (4)k - 1) -шаров в 6k-Космос", Анналы математики, Вторая серия, 75 (3): 452–466, Дои:10.2307/1970208, JSTOR  1970208
• Хасс, Джоэл (1998), «Алгоритмы распознавания узлов и 3-многообразий», Хаос, солитоны и фракталы, 9 (4–5): 569–581, arXiv:математика / 9712269, Bibcode:1998CSF ..... 9..569H, Дои:10.1016 / S0960-0779 (97) 00109-4
• Хост, Джим; Тистлтуэйт, Морвен; Недели, Джеффри (1998), «Первые 1701935 узлов», Математика. Интеллигенсер, 20 (4): 33–48, Дои:10.1007 / BF03025227
• Хост, Джим (2005), "Перечисление и классификация узлов и звеньев", Справочник по теории узлов (PDF), Амстердам: Эльзевир
• Левин, Джером (1965), «Классификация дифференцируемых узлов», Анналы математики, Вторая серия, 1982 (1): 15–50, Дои:10.2307/1970561, JSTOR  1970561
• Концевич Максим (1993), "Инварианты узлов Васильева", И. М. Гельфанд Семинар, Adv. Советская математика., 2, Провиденс, Род-Айленд: Американское математическое общество, 16: 137–150, Дои:10.1090 / advsov / 016.2 / 04, ISBN  9780821841174
• Ликориш, В. Б. Раймонд (1997), Введение в теорию узлов, Тексты для выпускников по математике, Springer-Verlag, ISBN  978-0-387-98254-0
• Перко, Кеннет (1974), "О классификации узлов", Труды Американского математического общества, 45 (2): 262–6, Дои:10.2307/2040074, JSTOR  2040074
• Рольфсен, Дейл (1976), Узлы и ссылки, Серия лекций по математике, 7, Беркли, Калифорния: Опубликовать или погибнуть, ISBN  978-0-914098-16-4, Г-Н  0515288
• Шуберт, Хорст (1949), "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten", Heidelberger Akad. Wiss. Math.-Nat. Kl. (3): 57–104
• Серебро, Дэн (2006), "Странное происхождение теории узлов" (PDF), Американский ученый, 94 (2), стр. 158–165, Дои:10.1511/2006.2.158
• Саймон, Джонатан (1986), "Топологическая хиральность некоторых молекул", Топология, 25 (2): 229–235, Дои:10.1016/0040-9383(86)90041-8
• Сосинский, Алексей (2002), Узлы, математика с изюминкой, Издательство Гарвардского университета, ISBN  978-0-674-00944-8
• Тураев, В. Г. (1994), «Квантовые инварианты узлов и 3-многообразий», Исследования Де Грюйтера по математике, Берлин: Walter de Gruyter & Co., 18, arXiv:hep-th / 9409028, ISBN  978-3-11-013704-0
• Вайсштейн, Эрик В. «Схема уменьшенного узла». MathWorld. Вольфрам. Получено 8 мая 2013.
• Вайсштейн, Эрик В. «Редуцируемый переход». MathWorld. Вольфрам. Получено 8 мая 2013.
• Виттен, Эдвард (1989), «Квантовая теория поля и многочлен Джонса», Comm. Математика. Phys., 121 (3): 351–399, Bibcode:1989CMaPh.121..351W, Дои:10.1007 / BF01217730
• Зееман, Э. (1963), «Комбинаторные шары без узлов», Анналы математики, Вторая серия, 78 (3): 501–526, Дои:10.2307/1970538, JSTOR  1970538

дальнейшее чтение

Вводные учебники

Есть несколько введений в теорию узлов. Классическое введение для аспирантов или студентов продвинутого уровня - (Рольфсен 1976 ). Другие хорошие тексты из ссылок (Адамс 2001 ) ошибка harv: цель отсутствует: CITEREFAdams2001 (Помогите) и (Ликориш 1997 ). Адамс неформален и доступен по большей части для старшеклассников. Lickorish - это строгий вводный курс для аспирантов, охватывающий хорошее сочетание классических и современных тем.

• Бурде, Герхард; Цишанг, Хайнер (1985), Узлы, Исследования Де Грюйтера по математике, 5, Вальтер де Грюйтер, ISBN  978-3-11-008675-1
• Кроуэлл, Ричард Х.; Фокс, Ральф (1977). Введение в теорию узлов. ISBN  978-0-387-90272-2.
• Кауфман, Луи Х. (1987), На узлах, ISBN  978-0-691-08435-0
• Кауфман, Луи Х. (2013), Узлы и физика (4-е изд.), World Scientific, ISBN  978-981-4383-00-4

Обзоры

• Menasco, Уильям В .; Thistlethwaite, Морвен, ред. (2005), Справочник по теории узлов, Эльзевьер, ISBN  978-0-444-51452-3
  • В справочнике Menasco и Thistlethwaite изучается набор тем, имеющих отношение к текущим исследовательским тенденциям, доступным для продвинутых студентов, но интересным для профессиональных исследователей.
• Ливио, Марио (2009), "Глава 8: Неоправданная эффективность?", Бог - математик?, Simon & Schuster, стр. 203–218, ISBN  978-0-7432-9405-8

внешние ссылки

• «Математика и узлы» Это онлайн-версия выставки "PopMath RoadShow" Королевского общества 1989 года. Его цель состояла в том, чтобы использовать узлы, чтобы представить методы математики широкой публике.

История

• Томсон, сэр Уильям (1867), «О вихревых атомах», Труды Королевского общества Эдинбурга, VI: 94–105
• Силлиман, Роберт Х. (декабрь 1963 г.), «Уильям Томсон: дымовые кольца и атомизм девятнадцатого века», Исида, 54 (4): 461–474, Дои:10.1086/349764, JSTOR  228151
• Кино современного воссоздания эксперимента Тэйта с кольцами дыма
• История теории узлов (на домашней странице Эндрю Раники )

Узловые столы и программное обеспечение

• KnotInfo: Таблица инвариантов узлов и ресурсы теории узлов
• Узел Атлас - подробная информация об отдельных узлах в таблицах узлов
• KnotPlot - программа для исследования геометрических свойств узлов
• Knotscape - программа для создания изображений сучков
• Knoutilus - онлайн-база данных и генератор изображений узлов
• KnotData.html — Wolfram Mathematica функция исследования узлов