Равномерные мутации симметрии мозаики - Uniform tiling symmetry mutations
| Сферические мозаики (п = 3..5) | ||
|---|---|---|
 *332 | 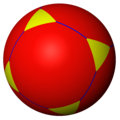 *432 | 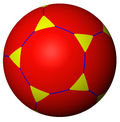 *532 |
| Евклидова плоская мозаика (п = 6) | ||
 *632 | ||
| Гиперболические плоские мозаики (п = 7...∞) | ||
 *732 |  *832 |  ... *∞32 |
В геометрия, а мутация симметрии это отображение фундаментальные области между двумя группами симметрии.[1] Они компактно выражены в орбифолдная запись. Эти мутации могут происходить от сферические мозаики к Евклидовы мозаики к гиперболические мозаики. Гиперболические мозаики также можно разделить на компактные, паракомпактные и дивергентные.
В однородные мозаики представляют собой простейшее применение этих мутаций, хотя более сложные паттерны могут быть выражены в фундаментальной области.
В этой статье выражены прогрессивные последовательности однородных мозаик внутри семейств симметрии.
Мутации орбифолдов
Орбифолды с одинаковой структурой могут изменяться между разными классами симметрии, в том числе в областях кривизны от сферической до евклидовой и гиперболической. В этой таблице показаны классы мутаций.[1] Эта таблица не является полной для возможных гиперболических орбифолдов.
| Орбифолд | Сферический | Евклидово | Гиперболический |
|---|---|---|---|
| о | - | о | - |
| pp | 22, 33 ... | ∞∞ | - |
| * пп | *22, *33 ... | *∞∞ | - |
| п* | 2*, 3* ... | ∞* | - |
| p × | 2×, 3× ... | ∞× | |
| ** | - | ** | - |
| *× | - | *× | - |
| ×× | - | ×× | - |
| PPP | 222 | 333 | 444 ... |
| pp * | - | 22* | 33* ... |
| pp × | - | 22× | 33×, 44× ... |
| pqq | 222, 322 ... , 233 | 244 | 255 ..., 433 ... |
| pqr | 234, 235 | 236 | 237 ..., 245 ... |
| pq * | - | - | 23*, 24* ... |
| pq × | - | - | 23×, 24× ... |
| p * q | 2*2, 2*3 ... | 3*3, 4*2 | 5*2 5*3 ..., 4*3, 4*4 ..., 3*4, 3*5 ... |
| *п* | - | - | *2* ... |
| * p × | - | - | *2× ... |
| pppp | - | 2222 | 3333 ... |
| pppq | - | - | 2223... |
| ppqq | - | - | 2233 |
| пп * п | - | - | 22*2 ... |
| p * qr | - | 2*22 | 3*22 ..., 2*32 ... |
| * ppp | *222 | *333 | *444 ... |
| * pqq | * п22, * 233 | *244 | *255 ..., *344... |
| * pqr | *234, *235 | *236 | *237..., *245..., *345 ... |
| п * ппп | - | - | 2*222 |
| * pqrs | - | *2222 | *2223... |
| * ppppp | - | - | *22222 ... |
| ... |
*п22 симметрия
Регулярные мозаики
| Космос | Сферический | Евклидово | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Плитка |  |  |  |  |  |  |  |  |  |  | ||
| Конфиг. | 2.2 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 | 211 | 212 | 2∞ |
| Космос | Сферический | Евклидово | ||||
|---|---|---|---|---|---|---|
| Плитка |  |  |  |  |  | |
| Конфиг. | 2.2 | 3.3 | 4.4 | 5.5 | 6.6 | ...∞.∞ |
Призма мозаики
| Космос | Сферический | Евклидово | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Плитка | |||||||||||
| Конфиг. | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | ...∞.4.4 |
Тайлинги с антипризмой
| Космос | Сферический | Евклидово | ||||||
|---|---|---|---|---|---|---|---|---|
| Плитка | ||||||||
| Конфиг. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | ...∞.3.3.3 |
*п32 симметрия
Регулярные мозаики
| *п32 изменения симметрии правильных мозаик: {3,п} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклид. | Компактный гипер. | Paraco. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| 3.3 | 33 | 34 | 35 | 36 | 37 | 38 | 3∞ | 312i | 39i | 36i | 33i |
| *п32 изменения симметрии правильных мозаик: {п,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
 |  |  |  |  |  |  |  |  |  |  |  |
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i, 3} | {9i, 3} | {6i, 3} | {3i, 3} |
Усеченные мозаики
| *п32 мутации симметрии усеченных мозаик: t {п,3} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | ||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | |
| Усеченный цифры |  |  |  |  |  |  |  |  |  |  | |
| Символ | т {2,3} | т {3,3} | т {4,3} | т {5,3} | т {6,3} | т {7,3} | т {8,3} | т {∞, 3} | т {12i, 3} | т {9i, 3} | т {6i, 3} |
| Triakis цифры |  |  |  |  |  |  |  | ||||
| Конфиг. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
| *п32 мутации симметрии усеченных мозаик: п.6.6 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п42 [n, 3] | Сферический | Евклид. | Компактный | Parac. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | ||
| Усеченный цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 2.6.6 | 3.6.6 | 4.6.6 | 5.6.6 | 6.6.6 | 7.6.6 | 8.6.6 | ∞.6.6 | 12i.6.6 | 9i.6.6 | 6i.6.6 | |
| н-кис цифры |  |  |  |  |  |  |  | |||||
| Конфиг. | V2.6.6 | V3.6.6 | V4.6.6 | V5.6.6 | V6.6.6 | V7.6.6 | V8.6.6 | V∞.6.6 | V12i.6.6 | V9i.6.6 | V6i.6.6 | |
Квазирегулярные мозаики
| Квазирегулярные мозаики: (3.n)2 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. * n32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| *332 [3,3] Тd | *432 [4,3] Очас | *532 [5,3] ячас | *632 [6,3] p6m | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | |||
| Фигура |  |  |  |  |  |  |  |  |  |  | ||
| Фигура |  |  |  |  | ||||||||
| Вершина | (3.3)2 | (3.4)2 | (3.5)2 | (3.6)2 | (3.7)2 | (3.8)2 | (3.∞)2 | (3.12i)2 | (3.9i)2 | (3.6i)2 | ||
| Schläfli | г {3,3} | г {3,4} | г {3,5} | г {3,6} | г {3,7} | г {3,8} | г {3, ∞} | г {3,12i} | г {3,9i} | г {3,6i} | ||
| Coxeter | ||||||||||||
| Двойные форменные фигуры | ||||||||||||
| Двойной конф. |  В (3,3)2 |  V (3,4)2 |  В (3,5)2 |  В (3,6)2 |  В (3,7)2 |  V (3.8)2 |  V (3.∞)2 | |||||
| Мутации симметрии двойственных квазирегулярных мозаик: V (3.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| * n32 | Сферический | Евклидово | Гиперболический | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Плитка |  |  |  |  |  |  |  | ||||
| Конф. | В (3,3)2 | V (3,4)2 | В (3,5)2 | В (3,6)2 | В (3,7)2 | V (3.8)2 | V (3.∞)2 | ||||
Развернутые мозаики
| *п42 мутации симметрии расширенных мозаик: 3.4.п.4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | ||
| Фигура |  |  |  |  |  |  |  |  |  |  | ||
| Конфиг. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 | 3.4.12i.4 | 3.4.9i.4 | 3.4.6i.4 | |
| Симметрия *п32 [n, 3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | ||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3]... | *∞32 [∞,3] | |
| Фигура Конфиг. |  V3.4.2.4 |  V3.4.3.4 |  V3.4.4.4 |  V3.4.5.4 |  V3.4.6.4 |  V3.4.7.4 |  V3.4.8.4 |  V3.4.∞.4 |
Омниусеченные мозаики
| *п32 мутации симметрии полностью усеченных мозаик: 4.6.2n | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Сим. *п32 [п,3] | Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | |||||||
| *232 [2,3] | *332 [3,3] | *432 [4,3] | *532 [5,3] | *632 [6,3] | *732 [7,3] | *832 [8,3] | *∞32 [∞,3] | [12i, 3] | [9i, 3] | [6i, 3] | [3i, 3] | |
| Цифры |  |  |  |  |  |  |  |  |  |  |  | |
| Конфиг. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals |  |  |  |  |  |  |  |  |  |  |  |  |
| Конфиг. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
Курносые плитки
| п32 мутации симметрии курносых плиток: 3.3.3.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия п32 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 232 | 332 | 432 | 532 | 632 | 732 | 832 | ∞32 | |
| Курносый цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.3.3.2 | 3.3.3.3.3 | 3.3.3.3.4 | 3.3.3.3.5 | 3.3.3.3.6 | 3.3.3.3.7 | 3.3.3.3.8 | 3.3.3.3.∞ |
| Гироскоп цифры |  |  |  |  |  |  |  |  |
| Конфиг. | V3.3.3.3.2 | V3.3.3.3.3 | V3.3.3.3.4 | V3.3.3.3.5 | V3.3.3.3.6 | V3.3.3.3.7 | V3.3.3.3.8 | V3.3.3.3.∞ |
*п42 симметрия
Регулярные мозаики
| *п42 изменения симметрии правильных мозаик: {4,п} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Компактный гиперболический | Паракомпакт | ||||||||
 {4,3} |  {4,4} |  {4,5} |  {4,6} |  {4,7} |  {4,8}... |  {4,∞} | |||||
| *п42 мутации симметрии правильных мозаик: {п,4} | |||||||
|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Гиперболические мозаики | |||||
 |  |  |  |  |  |  | |
| 24 | 34 | 44 | 54 | 64 | 74 | 84 | ...∞4 |
Квазирегулярные мозаики
| *п42 изменения симметрии квазирегулярных мозаик: (4.п)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *4п2 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | |||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | [пя, 4] | |
| Цифры |  |  |  |  |  |  |  | |
| Конфиг. | (4.3)2 | (4.4)2 | (4.5)2 | (4.6)2 | (4.7)2 | (4.8)2 | (4.∞)2 | (4.пя)2 |
| *п42 изменения симметрии квазирегулярных двойственных мозаик: V(4.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия * 4n2 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | Некомпактный | ||||||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | [iπ / λ, 4] | ||||
| Плитка Конф. |  V4.3.4.3 |  V4.4.4.4 |  V4.5.4.5 |  V4.6.4.6 |  V4.7.4.7 |  V4.8.4.8 |  V4.∞.4.∞ | V4.∞.4.∞ | |||
Усеченные мозаики
| *п42 мутации симметрии усеченных мозаик: 4,2п.2п | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п42 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Paracomp. | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| Усеченный цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| н-кис цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
| *п42 мутации симметрии усеченных мозаик: п.8.8 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *п42 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Паракомпакт | |||||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | ||||
| Усеченный цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | 2.8.8 | 3.8.8 | 4.8.8 | 5.8.8 | 6.8.8 | 7.8.8 | 8.8.8 | ∞.8.8 | |||
| н-кис цифры |  |  |  |  |  |  |  |  | |||
| Конфиг. | V2.8.8 | V3.8.8 | V4.8.8 | V5.8.8 | V6.8.8 | V7.8.8 | V8.8.8 | V∞.8.8 | |||
Развернутые мозаики
| *п42 мутации симметрии расширенных мозаик: п.4.4.4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия [n, 4], (*п42) | Сферический | Евклидово | Компактный гиперболический | Paracomp. | |||||||
| *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4] | *∞42 [∞,4] | |||||
| Расширенный цифры |  |  |  |  |  |  |  | ||||
| Конфиг. | 3.4.4.4 | 4.4.4.4 | 5.4.4.4 | 6.4.4.4 | 7.4.4.4 | 8.4.4.4 | ∞.4.4.4 | ||||
| Ромбический цифры config. |  V3.4.4.4 |  V4.4.4.4 |  V5.4.4.4 |  V6.4.4.4 |  V7.4.4.4 |  V8.4.4.4 |  V∞.4.4.4 | ||||
Омниусеченные мозаики
| *п42 мутации симметрии полностью усеченных мозаик: 4.8.2n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *п42 [n, 4] | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| *242 [2,4] | *342 [3,4] | *442 [4,4] | *542 [5,4] | *642 [6,4] | *742 [7,4] | *842 [8,4]... | *∞42 [∞,4] | |
| Усеченный фигура |  4.8.4 |  4.8.6 |  4.8.8 |  4.8.10 |  4.8.12 |  4.8.14 |  4.8.16 |  4.8.∞ |
| Усеченный двойники |  V4.8.4 |  V4.8.6 |  V4.8.8 |  V4.8.10 |  V4.8.12 |  V4.8.14 |  V4.8.16 |  V4.8.∞ |
Курносые плитки
| 4п2 мутации симметрии курносых плиток: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия 4п2 | Сферический | Евклидово | Компактный гиперболический | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Курносый цифры |  |  |  |  |  |  |  |  |
| Конфиг. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Гироскоп цифры |  |  |  |  | ||||
| Конфиг. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
*п52 симметрия
Регулярные мозаики
| Сфера | Гиперболическая плоскость | |||||
|---|---|---|---|---|---|---|
 {5,3} |  {5,4} |  {5,5} |  {5,6} |  {5,7} |  {5,8} |  ...{5,∞} |
*п62 симметрия
Регулярные мозаики
| *п62 изменения симметрии правильных мозаик: {6,п} | ||||||||
|---|---|---|---|---|---|---|---|---|
| Сферический | Евклидово | Гиперболические мозаики | ||||||
 {6,2} |  {6,3} |  {6,4} |  {6,5} |  {6,6} |  {6,7} |  {6,8} | ... |  {6,∞} |
*п82 симметрия
Регулярные мозаики
| Космос | Сферический | Компактный гиперболический | Паракомпакт | |||||
|---|---|---|---|---|---|---|---|---|
| Плитка |  |  |  |  |  |  |  | |
| Конфиг. | 8.8 | 83 | 84 | 85 | 86 | 87 | 88 | ...8∞ |
Рекомендации
Источники
- Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Страсс, Симметрии вещей 2008, ISBN 978-1-56881-220-5 [1]
- От гиперболического 2-пространства к 3-му евклидовому пространству: мозаики и паттерны через топологию Стивен Хайд
