Диаграмма пространства-времени - Spacetime diagram

Мировая линия (желтый путь) фотон, который находится по адресу Икс = 0 в момент времени ct = 0.

Часть серии по
Пространство-время
Специальная теория относительности Общая теория относительности
Концепции пространства-времени Пространственно-временное многообразие Принцип эквивалентности Преобразования Лоренца Пространство Минковского
Общая теория относительности Введение в общую теорию относительности Математика общей теории относительности Уравнения поля Эйнштейна
Классическая гравитация Введение в гравитацию Закон всемирного тяготения Ньютона
Соответствующая математика Четыре вектора Выводы теории относительности Диаграммы пространства-времени Дифференциальная геометрия Искривленное пространство-время Математика общей теории относительности Топология пространства-времени

А диаграмма пространства-времени является графической иллюстрацией свойств пространства и времени в специальная теория относительности. Диаграммы пространства-времени позволяют качественно понять соответствующие явления, такие как замедление времени и сокращение длины без математических уравнений.

История местоположения объекта за все время отслеживает линию, называемую мировая линия, на диаграмме пространства-времени. Точки на диаграммах пространства-времени представляют фиксированное положение в пространстве и времени и называются События.

Самый известный класс диаграмм пространства-времени известен как Диаграммы Минковского, разработан Герман Минковски в 1908 году. Диаграммы Минковского - это двухмерные графики, которые изображают события как происходящие в вселенная состоящий из одного измерения пространства и одного измерения времени. В отличие от обычного графика расстояние-время, расстояние отображается по горизонтальной оси, а время - по вертикальной оси. Кроме того, время и пространство меры измерения выбраны таким образом, чтобы объект, движущийся со скоростью света, изображался под углом 45 ° к осям диаграммы.

Введение в кинетические диаграммы

Графики положения и времени

При изучении одномерной кинематики графики зависимости положения от времени (также называемые графиками расстояния от времени или графиками p-t) предоставляют полезные средства для описания движения. Особенности движения предметов демонстрируют форма и наклон линий.^[1] На прилагаемом рисунке изображенный объект удаляется от начала координат с постоянной скоростью 1,66 м / с в течение шести секунд, останавливается на пять секунд, затем возвращается в исходное положение в течение семи секунд с непостоянной скоростью.

На самом базовом уровне пространственно-временная диаграмма представляет собой просто график зависимости времени от положения с обменом направлениями осей на обычном графике p-t, то есть вертикальная ось относится к временным, а горизонтальная ось - к значениям пространственных координат. Особенно при использовании в специальная теория относительности (SR) временные оси диаграммы пространства-времени масштабируются со скоростью света c, и поэтому часто обозначаются ct. Это изменяет размерность адресуемой физической величины с <Время> в <Длина>, в соответствии с размером, связанным с пространственными осями, которые часто обозначаются Икс.

Стандартная конфигурация опорных кадров

Диаграмма Галилея двух систем отсчета в стандартной конфигурации.

Чтобы облегчить понимание того, как координаты пространства-времени, измеренные наблюдателями в разных системы отсчета, сравнивайте между собой, полезно работать с упрощенной настройкой. С осторожностью это позволяет упростить математику без потери общности сделанных выводов. Если отложить в сторону временную составляющую, два Галилеевы системы отсчета (т.е. обычные 3-пространственные системы отсчета), S и S '(произносится как «S prime»), в каждой из которых наблюдатели O и O' находятся в состоянии покоя в соответствующих системах отсчета, но измеряют другой как движущийся со скоростью ±v говорят, что находятся в стандартная конфигурация, когда:

• В Икс, у, z Оси кадра S ориентированы параллельно соответствующим штрихованным осям кадра S '.
• Система отсчета S ′ движется в Икс-направление кадра S с постоянной скоростью v как измерено в кадре S.
• Истоки систем отсчета S и S ′ совпадают для времени т = 0 в кадре S и т′ = 0 в системе отсчета S ′.^[2]:107

Эта пространственная настройка отображается на прилагаемом рисунке, на котором временные координаты отдельно помечены как величины. т и т '.

На следующем этапе упрощения часто можно учитывать только направление наблюдаемого движения и игнорировать два других пространственных компонента, что позволяет Икс и ct должны быть построены в виде двумерных пространственно-временных диаграмм, как указано выше.

Нерелятивистские "диаграммы пространства-времени"

В ньютоновской физике для обоих наблюдателей событие в точке А приписывается одному и тому же моменту времени.

Черные топоры с надписью Икс и ct на соседней диаграмме представлена ​​система координат наблюдателя, называемого «в состоянии покоя», и который находится в Икс = 0. Мировая линия этого наблюдателя идентична ct ось времени. Каждая линия, параллельная этой оси, также будет соответствовать объекту в состоянии покоя, но в другом положении. Синяя линия описывает объект, движущийся с постоянной скоростью. v вправо, например движущийся наблюдатель.

Эта синяя линия помечена ct′ может интерпретироваться как ось времени для второго наблюдателя. Вместе с Икс ось, одинаковая для обоих наблюдателей, представляет их систему координат. Поскольку системы отсчета имеют стандартную конфигурацию, оба наблюдателя согласны в расположении источник их систем координат. Оси движущегося наблюдателя не перпендикуляр друг к другу, и шкала на их оси времени растягивается. Чтобы определить координаты определенного события, необходимо построить две линии, каждая из которых параллельна одной из двух осей, проходящих через событие, и отсчитать их пересечения с осями.

Определение положения и времени события A в качестве примера на диаграмме приводит к одинаковому времени для обоих наблюдателей, как и ожидалось. Только для позиции возникают разные значения, потому что движущийся наблюдатель приблизился к позиции события A, так как т = 0. Как правило, все события на линии, параллельной Икс оси происходят одновременно для обоих наблюдателей. Есть только одно всемирное время т = т′, моделируя существование одной общей оси положения. С другой стороны, из-за двух разных осей времени наблюдатели обычно измеряют разные координаты одного и того же события. Этот графический перевод из Икс и т к Икс′ и т′ и наоборот описывается математически так называемым Преобразование Галилея.

Диаграммы Минковского

Обзор

В теории относительности каждый наблюдатель относит событие в точке A к разному времени и месту.

Диаграмма Минковского для различных скоростей заправленного кадра, который движется относительно незаштрихованного кадра. Пунктирные линии представляют световой конус вспышки света в начале координат.

Термин диаграмма Минковского относится к особой форме диаграммы пространства-времени, часто используемой в специальной теории относительности. Диаграмма Минковского - это двухмерное графическое изображение части Пространство Минковского, обычно там, где пространство было сокращено до одного измерения. Единицы измерения на этих диаграммах выбраны такими, чтобы световой конус на мероприятии состоит из строк склон плюс или минус один через это событие.^[3] Горизонтальные линии соответствуют обычному понятию одновременные события для неподвижного наблюдателя в начале координат.

Конкретная диаграмма Минковского иллюстрирует результат Преобразование Лоренца. Преобразование Лоренца связывает два инерциальные системы отсчета, где наблюдатель стационарный на мероприятии (0, 0) меняет скорость вдоль Икс-ось. Новая ось времени наблюдателя образует угол α с предыдущей временной осью, с α < π/4. В новой системе координат одновременные события лежат параллельно линии, наклоненной α к предыдущим строкам одновременности. Это новый Икс-ось. И исходный набор осей, и набор осей со штрихом обладают тем свойством, что они ортогональны относительно оси. Внутренний продукт Минковского или же релятивистский скалярный продукт.

Каким бы ни был размер α, линия т = Икс образует универсальный^[4] биссектриса.

Пространство и время меры измерения на осях можно, например, принять одну из следующих пар:

• Единицы длиной ~ 30 сантиметров и наносекунды
• Астрономические единицы и интервалы около 8 минут 19 секунд (499 секунд)
• Световых лет и годы
• Световая секунда и второй

Таким образом, световые пути представлены линиями, параллельными биссектрисе между осями.

Математические детали

Угол α между Икс и Икс′ оси будут идентичны осям между осями времени ct и ct′. Это следует из второго постулата специальной теории относительности, согласно которому скорость света одинакова для всех наблюдателей, независимо от их относительного движения (см. Ниже). Угол α дан кем-то^[5]

${displaystyle an alpha = {frac {v} {c}} = eta.}$

Разные масштабы по осям.

Соответствующий импульс от Икс и т к Икс′ и т′ и наоборот математически описывается Преобразование Лоренца, что можно записать

${displaystyle {egin {align} ct '& = gamma (ct-eta x), x' & = gamma (x-vt) end {align}}}$

куда ${displaystyle gamma = (1- эта ^ {2}) ^ {- 1/2}}$ это Фактор Лоренца. Применяя преобразование Лоренца, оси пространства-времени, полученные для усиленного кадра, всегда будут соответствовать сопряженные диаметры пары гиперболы.

На диаграмме Минковского оси пространства-времени с усилением и без него, как правило, имеют неодинаковые единицы длины. Если U - единичная длина по осям ct и Икс соответственно единичная длина по осям ct′ и Икс′ является:^[6]

${displaystyle U '= U {sqrt {frac {1+ eta ^ {2}} {1- eta ^ {2}}}} ,.}$

В ct- ось представляет собой мировую линию часов, находящихся в S, с U представляющий продолжительность между двумя событиями, происходящими на этой мировой линии, также называемые подходящее время между этими событиями. Длина U на Икс- ось представляет собой оставшуюся длину или подходящая длина стержня, покоящегося в S. То же самое можно применить и к расстоянию. U′ на ct′- и Икс′- оси для часов и стержней, покоящихся в S′.

История

Альберт Эйнштейн открыл специальную теорию относительности в 1905 году,^[7] с Герман Минковски предоставив его графическое изображение в 1908 году.^[8]

В статье Минковского 1908 года было три диаграммы: сначала для иллюстрации преобразования Лоренца, затем для разделения плоскости световым конусом и, наконец, для иллюстрации мировых линий.^[8] Первая диаграмма использовала ветвь гипербола единиц ${displaystyle t ^ {2} -x ^ {2} = 1}$ показать местонахождение единицы подходящее время в зависимости от скорости, что демонстрирует замедление времени. На второй диаграмме показана сопряженная гипербола для калибровки пространства, где подобное растяжение оставляет впечатление Фицджеральд сокращение. В 1914 г. Людвик Зильберштейн^[9] включены диаграмма "представления Минковского преобразования Лоренца". Эта диаграмма включала единичную гиперболу, сопряженную ей и пару сопряженные диаметры. С 1960-х годов версия этой более полной конфигурации называлась диаграммой Минковского и использовалась в качестве стандартной иллюстрации геометрия трансформации специальной теории относительности. Э. Т. Уиттакер указал, что принцип относительности равносильно произволу выбора радиуса гиперболы время на диаграмме Минковского. В 1912 г. Гилберт Н. Льюис и Эдвин Б. Уилсон применил методы синтетическая геометрия развивать свойства неевклидов плоскость с диаграммами Минковского.^[10][11]

Когда Тейлор и Уиллер сочинили Физика пространства-времени (1966), они сделали нет используют термин «диаграмма Минковского» для их геометрии пространства-времени. Вместо этого они включали признание вклада Минковского в философию в целом его новаторства 1908 года.^[12]

Диаграммы Лёделя

В то время как кадр покоя на диаграмме Минковского имеет ортогональные оси пространства-времени, система отсчета, движущаяся относительно системы покоя на диаграмме Минковского, имеет оси пространства-времени, которые образуют острый угол. Эта асимметрия диаграмм Минковского может вводить в заблуждение, поскольку специальная теория относительности постулирует, что любые два инерциальные системы отсчета должен быть физически эквивалентным. Диаграмма Лёделя - это альтернативная диаграмма пространства-времени, которая делает симметрию инерциальных опорных систем намного более очевидной.

Формулировка через срединную рамку

Рис.1: Вид в средней рамке

Рис.2: Симметричная диаграмма

Некоторые авторы показали, что существует система отсчета между покоящимися и движущимися, где их симметрия будет очевидна («средняя система»).^[13] В этом кадре два других кадра движутся в противоположных направлениях с одинаковой скоростью. Использование таких координат делает единицы длины и времени одинаковыми для обеих осей. Если β = v/c и γ = 1/√1 − β² дается между ${displaystyle S}$ и ${displaystyle S ^ {prime}}$, то эти выражения связаны со значениями в их медианном фрейме S₀ следующее:^[13][14]

${displaystyle {egin {align} (1) && eta & = {frac {2 eta _ {0}} {1+ {eta _ {0}} ^ {2}}}, (2) && eta _ {0) } & = {frac {gamma -1} {eta gamma}}. конец {выровнено}}}$

Например, если β = 0.5 между ${displaystyle S}$ и ${displaystyle S ^ {prime}}$, то по (2) они движутся в своей медианной системе отсчета S₀ примерно с ±0.268c каждый в противоположных направлениях. С другой стороны, если β₀ = 0.5 в S₀, то по (1) относительная скорость между ${displaystyle S}$ и ${displaystyle S ^ {prime}}$ в их собственных рамах отдыха 0.8c. Строительство осей ${displaystyle S}$ и ${displaystyle S ^ {prime}}$ выполняется обычным методом с использованием загар α = β₀ относительно ортогональных осей срединной рамки (рис. 1).

Однако оказывается, что при рисовании такой симметричной диаграммы можно вывести отношения диаграммы даже без упоминания медианного кадра и β₀ вообще. Вместо этого относительная скорость β = v/c между ${displaystyle S}$ и ${displaystyle S ^ {prime}}$ можно напрямую использовать в следующей конструкции, дающей тот же результат:^[15]

Если φ угол между осями ct′ и ct (или между Икс и Икс′), и θ между осями Икс′ и ct′дается:^{[15][16][17][18]}

${displaystyle {egin {выровнено} sin varphi = cos heta & = eta, cos varphi = sin heta & = {frac {1} {gamma}}, an varphi = cot heta & = eta cdot gamma .end {выровнено} }}$

Два метода построения очевидны из рис.2: (а) Икс- ось проведена перпендикулярно оси ct′ось, Икс′ и ct- оси складываются под углом φ; (б) Икс′ - ось нарисована под углом θ с уважением к ct′ось, Икс-ось добавлена ​​перпендикулярно оси ct′ось и ct-ось перпендикулярна оси Икс′-ось.

На диаграмме Минковского длины на странице нельзя напрямую сравнивать друг с другом из-за коэффициента деформации между единичными длинами осей на диаграмме Минковского. В частности, если ${displaystyle U}$ и ${displaystyle U ^ {prime}}$ являются длинами блоков осей покоя и перемещение оси рамы, соответственно, в диаграмме Минковского, то две длины единичные искажен относительно друг друга с помощью формулы:

${displaystyle {egin {align} U ^ {prime} & = U {sqrt {frac {1+ eta ^ {2}} {1- eta ^ {2}}}} end {align}}}$

Напротив, на симметричной диаграмме Лёделя оба ${displaystyle S}$ и ${displaystyle S ^ {prime}}$ Оси рамы деформируются на один и тот же коэффициент относительно средней рамы и, следовательно, имеют одинаковую единицу длины. Это означает, что для пространственно-временной диаграммы Лёдела мы можем напрямую сравнивать длину пространства-времени между разными кадрами, как они появляются на странице; масштабирование / преобразование единичной длины между кадрами не требуется из-за симметричной природы диаграммы Лёделя.

История

• Макс Борн (1920) нарисовали диаграммы Минковского, поместив ct′-ось почти перпендикулярна оси Икс-оси, а также ct- ось к Икс′-оси, чтобы продемонстрировать сокращение длины и замедление времени в симметричном случае двух стержней и двух часов, движущихся в противоположном направлении.^[19]
• Дмитрий Мириманов (1921) показал, что всегда существует срединная система отсчета относительно двух относительно движущихся систем отсчета, и вывел отношения между ними из преобразования Лоренца. Однако он не дал графического представления в виде диаграммы.^[13]
• Симметричные диаграммы систематически разрабатывались Пол Грюнер в сотрудничестве с Йозефом Заутером в двух статьях в 1921 году. Им были продемонстрированы релятивистские эффекты, такие как сокращение длины и замедление времени, а также некоторые связи с ковариантными и контравариантными векторами.^[16][17] Грюнер расширил этот метод в своих последующих статьях (1922-1924), а также отдал должное лечению Мириманова.^{[20][21][22][23][24][25]}
• Построение симметричных диаграмм Минковского было позже независимо переоткрыто несколькими авторами. Например, начиная с 1948 г. Энрике Лёдел Палумбо опубликовал серию статей на испанском языке, в которых подробно описал такой подход.^[26][27] В 1955 г. Анри Амар также опубликовал статью, в которой описывались такие отношения, и отдал должное Лёделю в следующей статье в 1957 году.^[28][29] Некоторые авторы учебники использовать симметричные диаграммы Минковского, обозначая Диаграммы Лёделя.^[15][18]

Релятивистские явления в диаграммах

Замедление времени

Релятивистское замедление времени, как показано на двух диаграммах пространства-времени Лёделя. Оба наблюдателя считают, что часы другого идут медленнее.

Релятивистское замедление времени, как показано на единственной диаграмме пространства-времени Лёделя. Оба наблюдателя считают, что часы другого идут медленнее.

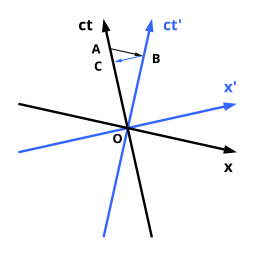
Релятивистское замедление времени относится к тому факту, что часы (показывая их подходящее время в своей системе покоя), который движется относительно наблюдателя, работает медленнее. Ситуация изображена на симметричных диаграммах Лёделя справа. Обратите внимание, что мы можем сравнивать длины пространства-времени на странице напрямую друг с другом из-за симметричной природы диаграммы Лёделя.

Предполагается, что наблюдатель, система отсчета которого задается черными осями, движется от начала координат O к A. Движущиеся часы имеют систему отсчета, заданную синими осями, и движутся от O к B. Для черного наблюдателя все события происходят одновременно. с событием в точке A расположены на прямой, параллельной его пространственной оси. Эта линия проходит через A и B, поэтому A и B одновременны из системы отсчета наблюдателя с черными осями. Однако часы, движущиеся относительно черного наблюдателя, отмечают время по синей оси времени. Это представлено расстоянием от O до B. Таким образом, наблюдатель в точке A с черными осями замечает, что их часы показывают расстояние от O до A, в то время как они наблюдают, как часы движутся относительно него или нее, чтобы определить расстояние от O до B. Из-за того, что расстояние от O до B меньше, чем расстояние от O до A, они заключают, что время, прошедшее на часах, движущихся относительно них, меньше, чем на их собственных часах.

Второй наблюдатель, переместившись вместе с часами от O к B, будет утверждать, что другие часы достигли только C до этого момента, и поэтому эти часы идут медленнее. Причина этих, казалось бы, парадоксальных утверждений - различное определение событий, происходящих синхронно в разных местах. В силу принципа относительности вопрос о том, кто прав, не имеет ответа и не имеет смысла.

Уменьшение длины

Релятивистское сокращение длины, как показано на двух диаграммах пространства-времени Лёделя. Оба наблюдателя рассматривают объекты, движущиеся вместе с другим наблюдателем, как более короткие.

Релятивистское сокращение длины, как показано на единственной диаграмме пространства-времени Лёделя. Оба наблюдателя рассматривают объекты, движущиеся вместе с другим наблюдателем, как более короткие.

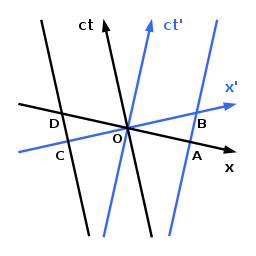
Релятивистское сокращение длины относится к тому факту, что линейка (указывая на подходящая длина в своей системе покоя), который движется относительно наблюдателя, сокращается / сокращается. Ситуация изображена на симметричных диаграммах Лёделя справа. Обратите внимание, что мы можем сравнивать длины пространства-времени на странице напрямую друг с другом из-за симметричной природы диаграммы Лёделя.

Предполагается, что наблюдатель снова движется по ct-ось. Предполагается, что мировые линии концов движущегося относительно него объекта движутся по ct′-оси и параллельной линии, проходящей через A и B. Для этого наблюдателя конечные точки объекта в т = 0 являются O и A. Для второго наблюдателя, движущегося вместе с объектом, так что для него объект находится в состоянии покоя, он имеет надлежащую длину OB на т′ = 0. Из-за OA . объект сжимается для первого наблюдателя.

Второй наблюдатель будет утверждать, что первый наблюдатель оценил конечные точки объекта в точках O и A соответственно и, следовательно, в разное время, что тем временем приведет к неверному результату из-за его движения. Если второй наблюдатель исследует длину другого объекта с конечными точками, движущимися вдоль ct-ось и параллельную линию, проходящую через C и D, он заключает, таким же образом этот объект должен быть сокращен от OD до OC. Каждый наблюдатель оценивает объекты, движущиеся вместе с другим наблюдателем, которые должны быть сжаты. Эта кажущаяся парадоксальной ситуация снова является следствием относительности одновременности, как показывает анализ с помощью диаграммы Минковского.

Для всех этих соображений предполагалось, что оба наблюдателя принимают во внимание скорость света и свое расстояние до всех событий, которые они видят, чтобы определить фактическое время, в которое эти события происходят с их точки зрения.

Постоянство скорости света

Диаграмма Минковского для трех систем координат. Для скоростей относительно системы черным цветом v′ = 0.4c и v″ = 0.8c держит.

Другой постулат специальной теории относительности - постоянство скорости света. В нем говорится, что любой наблюдатель в инерциальной системе отсчета, измеряющий скорость света в вакууме относительно себя, получает одно и то же значение независимо от его собственного движения и движения источника света. Это утверждение кажется парадоксальным, но оно немедленно следует из дифференциального уравнения, дающего его, и диаграмма Минковского согласуется с ним. Это также объясняет результат Эксперимент Майкельсона-Морли что считалось загадкой до того, как была открыта теория относительности, когда фотоны считались волнами, проходящими через необнаруживаемую среду.

Для мировых линий фотонов, проходящих через начало координат в разных направлениях Икс = ct и Икс = −ct держит. Это означает, что любое положение на такой мировой линии соответствует шагам на Икс- и ct- оси равной абсолютной величины. Из правила считывания координат в системе координат с наклонными осями следует, что две мировые линии являются биссектрисами угла Икс- и ct-акси. Диаграмма Минковского показывает, что они являются биссектрисами угла Икс'- и ct′-акси тоже. Это означает, что оба наблюдателя измеряют одинаковую скорость. c для обоих фотонов.

К этой диаграмме Минковского можно добавить дополнительные системы координат, соответствующие наблюдателям с произвольными скоростями. Для всех этих систем обе мировые линии фотонов представляют собой биссектрисы углов осей. Чем больше относительная скорость приближается к скорости света, тем больше оси приближаются к соответствующей биссектрисе угла. В ${displaystyle x}$ ось всегда более плоская, а временная ось круче мировых линий фотонов. Масштабы на обеих осях всегда идентичны, но обычно отличаются от масштабов других систем координат.

Скорость света и причинность

Прошлое и будущее относительно происхождения. Для серых областей соответствующая временная классификация невозможна.

Прямые линии, проходящие через начало координат, которые круче, чем обе мировые линии фотонов, соответствуют объектам, движущимся медленнее скорости света. Если это применимо к объекту, то это применимо с точки зрения всех наблюдателей, потому что мировые линии этих фотонов являются биссектрисами углов для любой инерциальной системы отсчета. Следовательно, любая точка выше начала координат и между мировыми линиями обоих фотонов может быть достигнута со скоростью, меньшей, чем скорость света, и может иметь причинно-следственную связь с началом координат. Эта область - абсолютное будущее, потому что любое событие там происходит позже по сравнению с событием, представленным источником, независимо от наблюдателя, что графически очевидно из диаграммы Минковского.

Следуя тому же аргументу, диапазон ниже начала координат и между мировыми линиями фотонов является абсолютным прошлым относительно начала координат. Любое событие там определенно принадлежит прошлому и может быть причиной следствия в начале.

Связь между любыми такими парами событий называется подобный времени, потому что они имеют временное расстояние больше нуля для всех наблюдателей. Прямая линия, соединяющая эти два события, всегда является временной осью возможного наблюдателя, для которого они происходят в одном и том же месте. Два события, которые можно связать как раз со скоростью света, называются легкий.

В принципе, к диаграмме Минковского можно добавить еще одно измерение пространства, что приведет к трехмерному представлению. В этом случае диапазоны будущего и прошлого становятся шишки вершины касаются друг друга в начале. Они называются световые конусы.

Скорость света как предел

Отправка сообщения со сверхсветовой скоростью от O через A до B в прошлое. Оба наблюдателя считают временной порядок пар событий O и A, а также A и B различным.

Следуя тому же аргументу, все прямые линии, проходящие через начало координат и более горизонтальные, чем мировые линии фотонов, будут соответствовать движущимся объектам или сигналам. быстрее света независимо от скорости наблюдателя. Следовательно, ни одно событие за пределами световых конусов не может быть достигнуто из источника, даже с помощью светового сигнала, ни с помощью какого-либо объекта или сигнала, движущегося со скоростью меньше скорости света. Такие пары событий называются космический потому что они имеют конечное пространственное расстояние, отличное от нуля для всех наблюдателей. С другой стороны, прямая линия, соединяющая такие события, всегда является осью пространственных координат возможного наблюдателя, для которого они происходят одновременно. Путем небольшого изменения скорости этой системы координат в обоих направлениях всегда можно найти две инерциальные системы отсчета, наблюдатели которых оценивают хронологический порядок этих событий как разный.

Следовательно, объект, движущийся со скоростью, превышающей скорость света, скажем от O к A на прилагаемой диаграмме, будет означать, что для любого наблюдателя, наблюдающего за объектом, движущимся от O к A, может быть найден другой наблюдатель (движущийся со скоростью меньше скорости света с относительно первого), для которого объект движется от A к O. Вопрос о том, какой наблюдатель прав, не имеет однозначного ответа и, следовательно, не имеет физического смысла. Любой такой движущийся объект или сигнал нарушит принцип причинности.

Кроме того, любые общие технические средства передачи сигналов быстрее скорости света позволят передать информацию в собственное прошлое отправителя. На диаграмме наблюдатель в точке O в Икс-ct система отправляет сообщение, движущееся быстрее света, к A. В точке A его получает другой наблюдатель, перемещающийся так, чтобы находиться в Икс′-ct′ система, которая отправляет его обратно, снова быстрее света, прибывает в B. Но B находится в прошлом по сравнению с O. Абсурдность этого процесса становится очевидной, когда оба наблюдателя впоследствии подтверждают, что они вообще не получали сообщения, но все сообщения были направлена ​​на другого наблюдателя, как это графически видно на диаграмме Минковского. Более того, если бы можно было ускорить наблюдателя до скорости света, их оси пространства и времени совпадали бы с их биссектрисой угла. Система координат рухнет, в соответствии с тем, что из-за замедление времени, время фактически перестало бы течь для них.

Эти соображения показывают, что скорость света как предел является следствием свойств пространства-времени, а не свойств объектов, таких как технологически несовершенные космические корабли. Таким образом, запрет на движение со скоростью, превышающей скорость света, не имеет ничего общего с электромагнитными волнами или светом, а является следствием структуры пространства-времени.

Наблюдатели с ускорением

Мгновенно движущиеся инерциальные системы отсчета вдоль мировой линии быстро ускоряющегося наблюдателя (в центре).

В анимации справа вертикальное направление указывает время, а горизонтальное указывает расстояние. Пунктирная линия - мировая линия ускоряющегося наблюдателя, а маленькие точки - определенные события в пространстве-времени.

Если представить каждое событие как мигание света, то события, которые проходят две диагональные линии в нижней половине изображения (световой конус прошедшего времени наблюдателя в начале координат), являются событиями, видимыми наблюдателю. Наклон мировой линии (отклонение от вертикали) дает наблюдателю относительную скорость. Обратите внимание, как мгновенно движущаяся инерциальная система отсчета изменяется при ускорении наблюдателя.

Смотрите также

• Пространство Минковского
• Диаграмма Пенроуза
• Быстрота

Рекомендации

• Энтони Френч (1968) Специальная теория относительности, страницы 82 и 83, Нью-Йорк: W W Norton & Company.
• E.N. Стекло (1975) "Повышение Лоренца и диаграммы Минковского" Американский журнал физики 43:1013,4.
• Н. Дэвид Мермин (1968) Пространство и время в специальной теории относительности, Глава 17 Диаграммы Минковского: Геометрия пространства-времени, страницы 155–99 Макгроу-Хилл.
• Риндлер, Вольфганг (2001). Теория относительности: специальная, общая и космологическая. Издательство Оксфордского университета. ISBN  0-19-850836-0.
• W.G.V. Россер (1964) Введение в теорию относительности, стр. 256, рис. 6.4, Лондон: Баттервортс.
• Эдвин Ф. Тейлор и Джон Арчибальд Уиллер (1963) Физика пространства-времени, страницы 27–38, Нью-Йорк: В. Х. Фриман и компания, Издание второе (1992).
• Вальтер, Скотт (1999), «Неевклидов стиль теории относительности Минковского» (PDF)в J. Gray (ed.), Символическая Вселенная: геометрия и физика, Oxford University Press, стр. 91–127. (см. страницу 10 электронной ссылки)

внешняя ссылка

СМИ, связанные с Диаграммы Минковского в Wikimedia Commons