Соревнование Штакельберга - Stackelberg competition

В Модель лидерства Штакельберга это стратегическая игра в экономика в котором сначала движется фирма-лидер, а затем последовательно движутся фирмы-последователи. Назван в честь немецкого экономиста. Генрих Фрайхер фон Штакельберг кто опубликовал Структура рынка и равновесие (Marktform und Gleichgewicht) в 1934 году описал модель.

В теория игры термины, игроки этой игры лидер и последователь и они конкурируют по количеству. Лидера Штакельберга иногда называют лидером рынка.

Есть еще некоторые ограничения на поддержание равновесия по Штакельбергу. Лидер должен знать ex ante что последователь наблюдает за его действием. Последователь не должен иметь никаких средств для совершения действий будущего лидера, не принадлежащего к Штакельбергу, и лидер должен это знать. В самом деле, если бы «последователь» мог совершить действие лидера по Штакельбергу и «лидер» знал бы об этом, лучшим ответом лидера было бы разыграть действие последователя по Штакельбергу.

Фирмы могут участвовать в соревновании по Штакельбергу, если у них есть какое-то преимущество, позволяющее им двигаться вперед. В более общем плане лидер должен иметь обязательство мощность. Наблюдаемое движение вперед - наиболее очевидное средство приверженности: как только лидер сделал свой ход, он не может его отменить - он привержен этому действию. Движение первым может быть возможным, если лидер был существующей монополией отрасли, а последователь - новым участником. Сохранение избыточных мощностей - еще одно средство обязательства.

Подигра идеальное равновесие по Нэшу

Модель Штакельберга может быть решена, чтобы найти подигра идеальное равновесие по Нэшу или равновесие (SPNE), то есть профиль стратегии, который лучше всего подходит каждому игроку, учитывая стратегии другого игрока и который влечет за собой участие каждого игрока в равновесие по Нэшу в каждом вспомогательная игра.

В самых общих чертах, пусть функция цены для отрасли (дуополии) будет ${ displaystyle P}$ ; цена - это просто функция от общего (отраслевого) выпуска, поэтому ${ Displaystyle P (q_ {1} + q_ {2})}$ где нижний индекс 1 представляет лидера, а 2 - ведомого. Предположим, фирма ${ displaystyle i}$ имеет структуру затрат ${ displaystyle C_ {i} (q_ {i})}$ . Модель решена обратная индукция. Лидер считает, что лучший ответ последователя, т.е. как он будем ответить, как только он заметил количество лидера. Затем лидер выбирает количество, которое максимизирует его выигрыш, ожидая предсказанной реакции ведомого. Последователь действительно наблюдает за этим и в состоянии равновесия выбирает ожидаемое количество в качестве ответа.

Для расчета SPNE функции наилучшего отклика следует сначала рассчитать (расчет движется «назад» из-за обратной индукции).

Прибыль фирмы 2 (последователя) равна выручке за вычетом затрат. Выручка - это произведение цены и количества, а стоимость определяется структурой затрат фирмы, поэтому прибыль составляет: ${ Displaystyle Pi _ {2} = P (q_ {1} + q_ {2}) cdot q_ {2} -C_ {2} (q_ {2})}$ . Лучший ответ - найти значение ${ displaystyle q_ {2}}$ что максимизирует ${ displaystyle Pi _ {2}}$ данный ${ displaystyle q_ {1}}$ , т.е. с учетом выпуска лидера (фирмы 1) находится выпуск, который максимизирует прибыль ведомого. Следовательно, максимум ${ displaystyle Pi _ {2}}$ относительно ${ displaystyle q_ {2}}$ нужно найти. Сначала дифференцируйте ${ displaystyle Pi _ {2}}$ относительно ${ displaystyle q_ {2}}$ :

{ displaystyle { frac { partial Pi _ {2}} { partial q_ {2}}} = { frac { partial P (q_ {1} + q_ {2})} { partial q_ { 2}}} cdot q_ {2} + P (q_ {1} + q_ {2}) - { frac { partial C_ {2} (q_ {2})} { partial q_ {2}}} .}

Установка этого значения в ноль для максимизации:

{ displaystyle { frac { partial Pi _ {2}} { partial q_ {2}}} = { frac { partial P (q_ {1} + q_ {2})} { partial q_ { 2}}} cdot q_ {2} + P (q_ {1} + q_ {2}) - { frac { partial C_ {2} (q_ {2})} { partial q_ {2}}} = 0.}

Ценности ${ displaystyle q_ {2}}$ которые удовлетворяют этому уравнению, являются лучшими ответами. Рассматривается функция наилучшего отклика лидера. Эта функция рассчитывается путем рассмотрения выхода ведомого как функции выхода лидера, как только что вычисленного.

Прибыль фирмы 1 (лидера) равна ${ Displaystyle Pi _ {1} = P (q_ {1} + q_ {2} (q_ {1})). q_ {1} -C_ {1} (q_ {1})}$ , где ${ displaystyle q_ {2} (q_ {1})}$ - количество ведомого как функция количества лидера, а именно вычисленная выше функция. Лучший ответ - найти значение ${ displaystyle q_ {1}}$ что максимизирует ${ displaystyle Pi _ {1}}$ данный ${ displaystyle q_ {2} (q_ {1})}$ , т.е. с учетом функции наилучшего отклика ведомого (фирмы 2), найден выпуск, который максимизирует прибыль лидера. Следовательно, максимум ${ displaystyle Pi _ {1}}$ относительно ${ displaystyle q_ {1}}$ нужно найти. Во-первых, дифференцируйте ${ displaystyle Pi _ {1}}$ относительно ${ displaystyle q_ {1}}$ :

{ displaystyle { frac { partial Pi _ {1}} { partial q_ {1}}} = { frac { partial P (q_ {1} + q_ {2})} { partial q_ { 2}}} cdot { frac { partial q_ {2} (q_ {1})} { partial q_ {1}}} cdot q_ {1} + { frac { partial P (q_ {1 } + q_ {2})} { partial q_ {1}}} cdot q_ {1} + P (q_ {1} + q_ {2} (q_ {1})) - { frac { partial C_ {1} (q_ {1})} { partial q_ {1}}}.}

Установка этого значения в ноль для максимизации:

{ displaystyle { frac { partial Pi _ {1}} { partial q_ {1}}} = { frac { partial P (q_ {1} + q_ {2})} { partial q_ { 2}}} cdot { frac { partial q_ {2} (q_ {1})} { partial q_ {1}}} cdot q_ {1} + { frac { partial P (q_ {1 } + q_ {2})} { partial q_ {1}}} cdot q_ {1} + P (q_ {1} + q_ {2} (q_ {1})) - { frac { partial C_ {1} (q_ {1})} { partial q_ {1}}} = 0.}

Примеры

Следующий пример является очень общим. Предполагается обобщенная линейная структура спроса.

{ displaystyle p (q_ {1} + q_ {2}) = { bigg (} a-b (q_ {1} + q_ {2}) { bigg)}}

и налагает некоторые ограничения на структуру затрат для простоты, так что проблема может быть решена.

{ displaystyle { frac { partial ^ {2} C_ {i} (q_ {i})} { partial q_ {i} cdot partial q_ {j}}} = 0, forall j}

и

{ displaystyle { frac { partial C_ {i} (q_ {i})} { partial q_ {j}}} = 0, j neq i}

для простоты вычислений.

Прибыль подписчика составляет:

{ displaystyle pi _ {2} = { bigg (} ab (q_ {1} + q_ {2}) { bigg)} cdot q_ {2} -C_ {2} (q_ {2}). }

Проблема максимизации разрешается (из общего случая):

{ displaystyle { frac { partial { bigg (} ab (q_ {1} + q_ {2}) { bigg)}} { partial q_ {2}}} cdot q_ {2} + ab ( q_ {1} + q_ {2}) - { frac { partial C_ {2} (q_ {2})} { partial q_ {2}}} = 0,}

{ displaystyle Rightarrow -bq_ {2} + ab (q_ {1} + q_ {2}) - { frac { partial C_ {2} (q_ {2})} { partial q_ {2}} } = 0,}

{ displaystyle Rightarrow q_ {2} = { frac {a-bq_ {1} - { frac { partial C_ {2} (q_ {2})} { partial q_ {2}}}} { 2b}}.}

Рассмотрим проблему лидера:

{ displaystyle Pi _ {1} = { bigg (} ab (q_ {1} + q_ {2} (q_ {1})) { bigg)} cdot q_ {1} -C_ {1} ( q_ {1}).}

Замена на ${ displaystyle q_ {2} (q_ {1})}$ из задачи последователя:

{ Displaystyle Pi _ {1} = { bigg (} ab { bigg (} q_ {1} + { frac {a-bq_ {1} - { frac { partial C_ {2} (q_ { 2})} { partial q_ {2}}}} {2b}} { bigg)} { bigg)} cdot q_ {1} -C_ {1} (q_ {1}),}

{ Displaystyle Rightarrow Pi _ {1} = { bigg (} { frac {ab.q_ {1} + { frac { partial C_ {2} (q_ {2})} { partial q_ { 2}}}} {2}}) { bigg)} cdot q_ {1} -C_ {1} (q_ {1}).}

Проблема максимизации разрешается (из общего случая):

{ Displaystyle { frac { partial pi _ {1}} { partial q_ {1}}} = { bigg (} { frac {a-2bq_ {1} + { frac { partial C_ { 2} (q_ {2})} { partial q_ {2}}}} {2}} { bigg)} - { frac { partial C_ {1} (q_ {1})} { partial q_ {1}}} = 0.}

Теперь решаем для ${ displaystyle q_ {1}}$ дает ${ displaystyle q_ {1} ^ {*}}$ , оптимальное действие лидера:

{ displaystyle q_ {1} ^ {*} = { frac {a + { frac { partial C_ {2} (q_ {2})} { partial q_ {2}}} - 2 cdot { frac { partial C_ {1} (q_ {1})} { partial q_ {1}}}} {2b}}.}

Это лучший ответ лидера на реакцию подчиненного в равновесии. Фактическое значение последователя теперь можно найти, введя его в рассчитанную ранее функцию реакции:

{ displaystyle q_ {2} ^ {*} = { frac {ab cdot { frac {a + { frac { partial C_ {2} (q_ {2})} { partial q_ {2}}}) -2 cdot { frac { partial C_ {1} (q_ {1})} { partial q_ {1}}}} {2b}} - { frac { partial C_ {2} (q_ {2 })} { partial q_ {2}}}} {2b}},}

{ displaystyle Rightarrow q_ {2} ^ {*} = { frac {a-3 cdot { frac { partial C_ {2} (q_ {2})} { partial q_ {2}}} + 2 cdot { frac { partial C_ {1} (q_ {1})} { partial q_ {1}}}} {4b}}.}

Все равновесия Нэша ${ displaystyle (q_ {1} ^ {*}, q_ {2} ^ {*})}$ . Ясно (если предполагается, что предельные затраты равны нулю, т. Е. Затраты по существу игнорируются), что лидер имеет значительное преимущество. Интуитивно понятно, что если бы лидер был не лучше, чем последователь, он бы просто принял Конкурс Курно стратегия.

Подключение количества последователей ${ displaystyle p_ {2}}$ , обратно в функцию наилучшего ответа лидера не даст ${ displaystyle p_ {1}}$ . Это потому, что, как только лидер взял на себя обязательство по выпуску и наблюдал за последователями, он всегда хочет уменьшить свой результат постфактум. Однако его неспособность сделать это позволяет ему получать более высокую прибыль, чем при использовании курса.

Экономический анализ

Представление в развернутой форме часто используется для анализа модели «лидер-последователь» Штакельберга. Также называется «Древо решений ”, Модель показывает комбинацию результатов и выплат, которые имеют обе фирмы в игре Штакельберга.

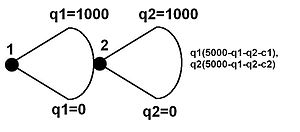
Игра Штакельберга, представленная в обширная форма

Изображение слева изображено в обширная форма игра Штакельберга. Выплаты показаны справа. Этот пример довольно простой. Существует базовая структура затрат, включающая только предельная стоимость (здесь нет фиксированная цена ). Функция спроса линейна, а эластичность спроса по цене равна 1. Однако это демонстрирует преимущество лидера.

Последователь хочет выбрать ${ displaystyle q_ {2}}$ чтобы максимизировать отдачу ${ displaystyle q_ {2} * (5000-q_ {1} -q_ {2} -c_ {2})}$ . Взяв производную первого порядка и приравняв ее к нулю (для максимизации), получаем ${ displaystyle q_ {2} = { frac {5000-q_ {1} -c_ {2}} {2}}}$ как максимальное значение ${ displaystyle q_ {2}}$ .

Лидер хочет выбирать ${ displaystyle q_ {1}}$ чтобы максимизировать отдачу ${ displaystyle q_ {1} * (5000-q_ {1} -q_ {2} -c_ {1})}$ . Однако в равновесии он знает, что ведомый выберет ${ displaystyle q_ {2}}$ как указано выше. Так что на самом деле лидер хочет максимизировать отдачу ${ displaystyle q_ {1} * (5000-q_ {1} - { frac {5000-q_ {1} -c_ {2}} {2}} - c_ {1})}$ (путем замены ${ displaystyle q_ {2}}$ для функции наилучшего отклика ведомого). По дифференцированию максимальный выигрыш определяется как ${ displaystyle q_ {1} = { frac {5000-2c_ {1} + c_ {2}} {2}}}$ . Подавая это в функцию лучшего отклика ведомого, получаем ${ displaystyle q_ {2} = { frac {5000 + 2c_ {1} -3c_ {2}} {4}}}$ . Предположим, что предельные издержки были равны для фирм (так что у лидера нет никаких рыночных преимуществ, кроме первого шага) и, в частности, ${ displaystyle c_ {1} = c_ {2} = 1000}$ . Лидер произведет 2000, а ведомый произведет 1000. Это даст лидеру прибыль (выигрыш) в размере двух миллионов, а ведомому - прибыль в один миллион. Просто двигаясь первым, лидер получает в два раза больше прибыли, чем последователь. Однако, Курно прибыль вот 1,78 миллиона за штуку (строго, ${ displaystyle (16/9) 10 ^ {6}}$ за штуку), поэтому лидер не многого приобрел, а ведомый потерял. Однако это зависит от конкретного примера. Могут быть случаи, когда руководитель Штакельберга имеет огромные выгоды, помимо прибыли Курно от такого подхода. монополия прибыли (например, если у лидера также было большое преимущество в структуре затрат, возможно, из-за лучшего производственная функция ). Также могут быть случаи, когда последователь действительно получает более высокую прибыль, чем лидер, но только потому, что, скажем, он имеет гораздо более низкие затраты. Такое поведение постоянно работает на дуополистических рынках, даже если фирмы асимметричны.

Достоверные и ненадежные угрозы со стороны последователя

Если после того, как лидер выбрал свое равновесное количество, ведомый отклонился от равновесия и выбрал какое-то неоптимальное количество, это не только навредило бы себе, но и могло бы повредить лидеру. Если последователь выберет гораздо большее количество, чем его лучший ответ, рыночная цена упадет, а прибыль лидера пострадает, возможно, ниже прибыли уровня Курно. В этом случае ведомый может объявить лидеру до начала игры, что, если лидер не выберет равновесное количество Курно, ведомый выберет отклоняющееся количество, которое повлияет на прибыль лидера. В конце концов, количество, выбранное лидером в равновесии, является оптимальным только в том случае, если ведомый также играет в равновесии. Однако лидеру ничего не угрожает. После того, как лидер выбрал свое равновесное количество, для ведомого было бы иррационально отклоняться, потому что это тоже могло бы пострадать. После того, как лидер сделал выбор, последователь будет лучше играть по пути равновесия. Следовательно, такая угроза со стороны последователя не вызывает доверия.

Однако в (неограниченно) повторяющейся игре Штакельберга ведомый может принять стратегию наказания, при которой он угрожает наказать лидера в следующем периоде, если он не выберет неоптимальную стратегию в текущем периоде. Эта угроза может быть правдоподобной, потому что для ведомого может быть рациональным наказать в следующем периоде, чтобы после этого лидер выбирал количества Курно.

Штакельберг по сравнению с Курно

Штакельберг и Курно модели похожи, потому что в обоих конкуренция по количеству. Однако, как видно, первый ход дает лидеру Штакельберга решающее преимущество. Есть также важное предположение о том, что идеальная информация в игре Штакельберга: ведомый должен соблюдать количество, выбранное лидером, в противном случае игра сводится к Курно. При неполной информации описанные выше угрозы могут быть достоверными. Если ведомый не может наблюдать за движением лидера, то для него уже не является иррациональным выбирать, скажем, количественный уровень Курно (фактически, это равновесное действие). Однако должно быть, что там является несовершенная информация и последователь является невозможно наблюдать за перемещением лидера, потому что для ведомого нерационально не наблюдать, если он может, после того, как лидер переместился. Если он может наблюдать, он будет так делать, чтобы принять оптимальное решение. Любая угроза со стороны последователя, утверждающего, что он не будет наблюдать, даже если это будет возможно, столь же недостоверна, как и указанные выше. Это пример того, как слишком много информации причиняет вред игроку. В соревновании Курно именно одновременность игры (несовершенство знания) не приводит ни к одному из игроков (при прочих равных условиях ) находясь в невыгодном положении.

Теоретико-игровые соображения

Как уже упоминалось, несовершенная информация в лидерской игре сводится к соревнованию Курно. Тем не менее, некоторые профили стратегии Курно поддерживаются как Равновесия Нэша но могут быть устранены как невероятные угрозы (как описано выше) путем применения концепция решения из совершенство подигры. В самом деле, именно это делает профиль стратегии Курно равновесием по Нэшу в игре Штакельберга, что не позволяет ему быть совершенной подигрой.

Рассмотрим игру Штакельберга (т. Е. Такую, которая удовлетворяет описанным выше требованиям для поддержания равновесия Штакельберга), в которой по какой-то причине лидер считает, что какое бы действие он ни предпринял, ведомый выберет количество Курно (возможно, лидер считает, что ведомый иррационально). Если лидер сыграл действие Штакельберга, (он считает), что ведомый сыграет Курно. Следовательно, для лидера играть Штакельберга неоптимально. Фактически, его лучший ответ (по определению равновесия Курно) - это играть количеством Курно. Как только он это сделает, лучший ответ соратника - сыграть Курно.

Рассмотрим следующие профили стратегии: лидер играет Курно; ведомый играет Курно, если лидер играет Курно, а ведомый играет Штакельберга, если лидер играет Штакельберга, и если лидер играет что-то еще, ведомый играет произвольную стратегию (следовательно, это фактически описывает несколько профилей). Этот профиль представляет собой равновесие по Нэшу. Как указывалось выше, игра по пути равновесия - лучший ответ на лучший ответ. Однако игра Курно была бы не лучшим ответом лидера, если бы его последователь играл Штакельберга, если бы он (лидер) играл Штакельберга. В этом случае лучшим ответом лидера будет игра Штакельберга. Следовательно, что делает этот профиль (или, скорее, эти профили) равновесием по Нэшу (или, скорее, равновесием по Нэшу), так это тот факт, что ведомый будет играть не-Штакельберга, если бы лидер играл Штакельберга.

Однако сам этот факт (то, что ведомый играл бы не-Штакельберга, если бы лидер играл Штакельберга) означает, что этот профиль не является равновесием по Нэшу для вспомогательной игры, начиная с того момента, когда лидер уже сыграл по Штакельбергу (вспомогательная игра вне равновесного пути). . Если лидер уже сыграл Штакельберга, лучший ответ ведомого - это сыграть Штакельберга (и, следовательно, это единственное действие, которое приводит к равновесию по Нэшу в этой подигре). Следовательно, профиль стратегии, которым является Курно, не идеален для подигр.

Сравнение с другими моделями олигополии

По сравнению с другими моделями олигополии,

Совокупный выпуск Штакельберга больше, чем совокупный выпуск Курно, но меньше совокупного выпуска. Бертран вывод.
Цена Штакельберга ниже, чем цена Курно, но больше, чем цена Бертрана.
Потребительский излишек Штакельберга больше, чем потребительский излишек Курно, но ниже, чем потребительский излишек Бертрана.
Совокупный объем производства по Штакельбергу больше, чем чистая монополия или картель, но меньше, чем идеально конкурентоспособный вывод.
Цена Штакельберга ниже, чем цена чистой монополии или картеля, но выше, чем совершенно конкурентоспособная цена.

Приложения

Концепция Штакельберга была распространена на динамические игры Штакельберга. См. Simaan и Cruz (1973a, 1973b). С добавлением времени в качестве измерения были обнаружены явления, не обнаруживаемые в статических играх, такие как нарушение принципа оптимальности лидером, Симаном и Крузом (1973b). Обзор приложений дифференциальных игр Штакельберга к цепочке поставок и каналам сбыта см. В He et al. (2007). В последние годы игры Штакельберга внесли большой вклад в обеспечение безопасности.^[1] где для сотрудников службы безопасности важно защитить какой-то ценный ресурс и найти для него любые потенциальные угрозы. Именно здесь персонал службы безопасности (лидер) сначала должен разработать свою стратегию, чтобы независимо от стратегии, принятой вором (последователем), ресурс оставался в безопасности.

Смотрите также

использованная литература

^ Браун, Джеральд (2006). «Защита критической инфраструктуры». Интерфейсы. 36 (6): 530–544. Дои:10.1287 / inte.1060.0252. HDL:10945/36732.

Х. фон Штакельберг, Структура рынка и равновесие: перевод 1-го издания на английский язык, Bazin, Urch & Hill, Springer 2011, XIV, 134 стр., ISBN 978-3-642-12585-0
М. Симаан и Дж. Б. Круз-младший, О стратегии Штакельберга в играх с ненулевой суммой, Журнал теории оптимизации и приложений, Vol. 11, № 5, май 1973 г., стр. 533–555.
М. Симаан и Дж. Б. Круз-младший, Дополнительные аспекты стратегии Штакельберга в играх с ненулевой суммой, Журнал теории оптимизации и приложений, Vol. 11, № 6, июнь 1973 г., стр. 613–626.
Он, X., Прасад, A., Сетхи, С., и Гутьеррес, Г. (2007) Обзор дифференциальных игровых моделей Штакельберга в каналах сбыта и сбыта продукции, Журнал системной науки и системной инженерии (JSSSE), 16 (4), декабрь 2007 г., стр. 385–413. Доступны на https://ssrn.com/abstract=1069162
Фуденберг, Д. и Тироль, Дж. (1993) Теория игры, MIT Press. (см. главу 3, раздел 1)
Гиббонс, Р. (1992) Учебник по теории игр, Комбайн-пшеничный сноп. (см. главу 2, раздел 1B)
Осборн, М.Дж. и Рубинштейн, А. (1994) Курс теории игр, MIT Press (см. Стр. 97-98)
Теория олигоплей стала простой, Глава 6 Экономика серфинга от Хью Диксон.

[1] Браун, Джеральд (2006). «Защита критической инфраструктуры». Интерфейсы. 36 (6): 530–544. Дои:10.1287 / inte.1060.0252. HDL:10945/36732.

[1]

Темы в теория игры
Определения	Кооперативная игра Решительность Эскалация обязательств Игра в расширенной форме Победа первого и второго игрока Сложность игры Графическая игра Иерархия убеждений Информационный набор Игра в нормальной форме Предпочтение Последовательная игра Одновременная игра Выбор одновременного действия Решенная игра Лаконичная игра
Равновесие концепции	равновесие по Нэшу Совершенство подигры Устойчивое равновесие по Мертенсу Байесовское равновесие по Нэшу Идеальное байесовское равновесие Дрожащая рука Правильное равновесие Эпсилон-равновесие Коррелированное равновесие Последовательное равновесие Квази-совершенное равновесие Эволюционно устойчивая стратегия Доминирование риска Ядро Значение Шепли Парето эффективность Равновесие Гиббса Квантовое равновесие отклика Самоподтверждающееся равновесие Сильное равновесие по Нэшу Марковское идеальное равновесие
Стратегии	Доминирующие стратегии Чистая стратегия Смешанная стратегия Аргумент кражи стратегии Око за око Мрачный спусковой крючок Сговор Обратная индукция Прямая индукция Марковская стратегия Затенение ставки
Классы игр	Симметричная игра Идеальная информация Повторная игра Сигнальная игра Показ игры Дешевый разговор Игра с нулевой суммой Конструкция механизма Проблема торга Стохастическая игра Среднее поле игры п-игровая игра Большая игра Пуассона Нетранзитивная игра Глобальная игра Строго определенная игра Возможная игра
Игры	Идти Шахматы Бесконечные шахматы Шашки Крестики-нолики Дилемма заключенного Игра по обмену подарками Необязательная дилемма заключенного Дилемма путешественника Координационная игра Курица Сороконожка игра Дилемма волонтера Долларовый аукцион Битва полов Охота на оленя Соответствующие пенни Ультиматум игра Камень ножницы Бумага Пиратская игра Диктаторская игра Игра в общественные блага Блотто игра Война на истощение Проблема с баром Эль Фарол Справедливое деление Ярмарка нарезки торта Игра Курно Тупик Дилемма закусочной Угадайте 2/3 среднего Покер куна Игра Нэша в торг Индукционные пазлы Доверительная игра Игра принцесс и монстров Проблема рандеву
Теоремы	Теорема о невозможности Эрроу Теорема согласия Ауманна Народная теорема Теорема о минимаксе Теорема Нэша Теорема очищения Принцип откровения Теорема Цермело
Ключ цифры	Альберт В. Такер Амос Тверски Антуан Огюстен Курно Ариэль Рубинштейн Клод Шеннон Даниэль Канеман Дэвид К. Левин Дэвид М. Крепс Дональд Б. Гиллис Дрю Фуденберг Эрик Маскин Гарольд В. Кун Герберт Саймон Эрве Мулен Жан Тироль Жан-Франсуа Мертенс Дженнифер Тур Чейес Джон Харсаньи Джон Мейнард Смит Джон Нэш Джон фон Нейман Кеннет Эрроу Кеннет Бинмор Леонид Гурвич Ллойд Шепли Мелвин Дрешер Меррилл М. Флуд Ольга Бондарева Оскар Моргенштерн Пол Милгром Пейтон Янг Райнхард Зельтен Роберт Аксельрод Роберт Ауманн Роберт Б. Уилсон Роджер Майерсон Сэмюэл Боулз Сюзанна Скотчмер Томас Шеллинг Уильям Викри
Смотрите также	All-pay аукцион Альфа – бета обрезка Парадокс Бертрана Ограниченная рациональность Комбинаторная теория игр Анализ конфронтации Сотрудничество Эволюционная теория игр Преимущество первого хода в шахматах Игровая механика Глоссарий теории игр Список теоретиков игр Список игр по теории игр Безвыигрышная ситуация Решение шахмат Топологическая игра Трагедия общественного достояния Тирания малых решений