Проблема Монти Холла - Monty Hall problem

В Проблема Монти Холла это головоломка в форме вероятность головоломка, по мотивам американского телеигрового шоу Давайте сделаем сделку и назван в честь своего первоначального хозяина, Монти Холл. Первоначально проблема была поставлена (и решена) в письме Стив Селвин к Американский статистик в 1975 г.[1][2] Он стал известен как вопрос из письма читателя, цитируемого в Мэрилин Вос Савант колонка "Спросите Мэрилин" в Парад журнал в 1990 году:[3]
Предположим, вы участвуете в игровом шоу, и вам предоставляется выбор из трех дверей: за одной дверью находится машина; позади остальных - козы. Вы выбираете дверь, скажем, №1, и хозяин, который знает, что за дверями, открывает другую дверь, скажем №3, в которой есть коза. Затем он говорит вам: «Вы хотите выбрать дверь № 2?» В ваших интересах менять свой выбор?
Вос Савант ответил, что участник должен перейти к другой двери.[3] Согласно стандартным предположениям, участники, которые переключаются, имеют 2/3 шанс выиграть машину, в то время как участники, которые придерживаются своего первоначального выбора, имеют только 1/3 шанс.
Приведенные вероятности зависят от конкретных предположений о том, как ведущий и участник выбирают свои двери. Ключевой вывод состоит в том, что в этих стандартных условиях информации о дверях 2 и 3 больше, чем было доступно в начале игры, когда дверь 1 была выбрана игроком: преднамеренное действие хозяина увеличивает ценность двери, которую он не делал. выбрал исключение, но не тот, который изначально был выбран участником. Другое понимание заключается в том, что переключение дверей - это другое действие, чем выбор между двумя оставшимися дверями наугад, поскольку первое действие использует предыдущую информацию, а второе - нет. Другие возможные варианты поведения, отличные от описанного, могут раскрыть другую дополнительную информацию или не раскрыть ее вовсе и дать разные вероятности. Еще одно понимание состоит в том, что ваши шансы на победу при переключении дверей напрямую связаны с вашим шансом выбрать выигрышную дверь в первую очередь: если вы выберете правильную дверь с первой попытки, переключение будет проигрышным; если вы с первого раза выберете не ту дверь, то переключение победит; ваш шанс выбрать правильную дверь с первой попытки - 1/3, а шанс выбрать не ту дверь - 2/3.
Многие читатели колонки Вос Савант отказывались верить, что переключение полезно, несмотря на ее объяснения. После того, как проблема появилась в Парад, около 10 000 читателей, в том числе около 1000 с Доктора философии, написали в журнал, большинство из них утверждали, что vos Savant был неправ.[4] Даже получив объяснения, моделирование и формальные математические доказательства, многие люди по-прежнему не принимают, что переключение - лучшая стратегия.[5] Пол Эрдёш, один из самых плодовитых математиков в истории, не был убежден, пока ему не показали компьютерное моделирование демонстрируя предсказанный результат Вос Саванта.[6]
Проблема в парадоксе достоверный типа, потому что правильный выбор (переключение дверей) таков нелогичный это может показаться абсурдным, но, тем не менее, очевидно, верно. Проблема Монти Холла математически тесно связана с более ранней Проблема трех узников и гораздо старше Парадокс коробки Бертрана.
Парадокс
Стив Селвин написал письмо в Американский статистик в 1975 году, описывая проблему на основе игрового шоу Давайте сделаем сделку,[1] в последующем письме назвал это «проблемой Монти Холла».[2] Задача математически эквивалентна Проблема трех узников описано в Мартин Гарднер столбец "Математические игры" в Scientific American в 1959 г.[7] и проблема трех оболочек, описанная в книге Гарднера Ага Попался.[8]
Та же проблема была повторена в письме Крейга Уитакера 1990 г. Мэрилин Вос Савант колонка "Спросите Мэрилин" в Парад:
Предположим, вы участвуете в игровом шоу, и вам предоставляется выбор из трех дверей: за одной дверью находится машина; позади остальных - козы. Вы выбираете дверь, скажем, №1, и хозяин, который знает, что за дверями, открывает другую дверь, скажем №3, в которой есть коза. Затем он говорит вам: «Вы хотите выбрать дверь № 2?» Выгодно ли менять свой выбор?[9]
Стандартные допущения
При стандартных предположениях вероятность выигрыша машины после переключения равна 2/3Ключом к этому решению является поведение хоста. Неясности в Парад версии не определяют явно протокол хоста. Однако решение Мэрилин вос Савант[3] напечатанный рядом с вопросом Уитакера подразумевает, что и Селвен[1] и савант[5] явно определить роль хоста следующим образом:
- Ведущий всегда должен открывать дверь, которую не выбрал участник.[10]
- Хозяин всегда должен открывать дверь, чтобы показать козу, но не машину.
- Хост всегда должен предлагать возможность переключиться между первоначально выбранной дверью и оставшейся закрытой дверью.
Когда любое из этих предположений изменяется, это может изменить вероятность выигрыша путем переключения дверей, как подробно описано в раздел ниже. Также обычно предполагается, что машина изначально спрятана за дверями случайным образом и что, если игрок сначала выбирает машину, то выбор хозяином того, какую дверь из козла открыть, является случайным.[11] Некоторые авторы, независимо или включительно, предполагают, что первоначальный выбор игрока также случаен.[1]
Простые решения
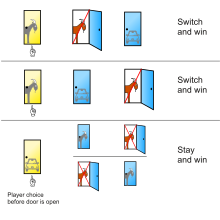
Решение, представленное Вос Савантом в Парад показывает три возможных варианта расположения одной машины и двух козлов за тремя дверями и результат пребывания или переключения после первоначального выбора двери 1 в каждом случае:[12]
За дверью 1 За дверью 2 За дверью 3 Результат, если оставаться у двери №1 Результат при переходе на предложенную дверь Козел Козел Машина Побеждает коза Выигрывает автомобиль Козел Машина Козел Побеждает коза Выигрывает автомобиль Машина Козел Козел Выигрывает автомобиль Побеждает коза
Игрок, который остается с первоначальным выбором, выигрывает только в одной из трех из этих равновероятных возможностей, в то время как игрок, который меняет позицию, выигрывает в двух из трех.
Интуитивно понятное объяснение состоит в том, что если участник сначала выбирает козу (2 из 3 дверей), то участник буду выиграть машину, переключившись, потому что другая коза больше не может быть выбрана, тогда как если участник сначала выбирает машину (1 из 3 дверей), участник не будет выиграть машину переключением.[13] Тот факт, что ведущий впоследствии обнаруживает козу в одной из неизбранных дверей, ничего не меняет в отношении начальной вероятности.

Большинство людей приходят к выводу, что переключение не имеет значения, потому что есть две закрытые двери и одна машина, и это выбор 50/50. Это будет верно, если хост открывает дверь случайным образом, но это не так; открытая дверь зависит от первоначального выбора игрока, поэтому предположение независимость не держит. Прежде чем ведущий откроет дверь, 1/3 вероятность, что машина находится за каждой дверью. Если машина находится за дверью 1, хост может открыть дверь 2 или дверь 3, поэтому вероятность того, что машина находится за дверью 1, и хост открывает дверь 3, равна 1/3 × 1/2 = 1/6. Если машина находится за дверью 2 (и игрок выбрал дверь 1), хозяин должен открыть дверь 3, поэтому вероятность того, что машина находится за дверью 2, и хост открывает дверь 3, равна 1/3 × 1 = 1/3. Это единственные случаи, когда ведущий открывает дверь 3, поэтому, если игрок выбрал дверь 1, а ведущий открывает дверь 3, вероятность того, что машина окажется за дверью 2, в два раза выше. Ключ в том, что если машина находится за дверью 2, хозяин должен открыть дверь 3, но если машина находится за дверью 1, хозяин может открыть любую дверь.
Другой способ понять решение - рассмотреть две исходные несобранные двери вместе.[14][15][16][17][18] В качестве Сесил Адамс кладет это,[14] «Монти, по сути, говорит: вы можете оставить себе одну дверь или две другие». В 2/3 шанс найти машину не изменился после открытия одной из этих дверей, потому что Монти, зная местонахождение машины, наверняка обнаружит козла. Таким образом, выбор игрока после того, как ведущий открывает дверь, ничем не отличается от того, если бы ведущий предлагал игроку возможность переключиться с исходной выбранной двери на набор обе остальные двери. Переключатель в этом случае явно дает игроку 2/3 вероятность выбора машины.


В качестве Кейт Девлин говорит,[15] «Открывая дверь, Монти говорит участнику:« Есть две двери, которые вы не выбрали, и вероятность того, что приз окажется за одной из них, составляет 2/3. Я помогу вам, используя свои знания о том, где находится приз, чтобы открыть одну из этих двух дверей, чтобы показать вам, что она не скрывает приз. Теперь вы можете воспользоваться этой дополнительной информацией. Выбранная вами дверь A имеет шанс 1 из 3 стать победителем. Я этого не изменил. Но, исключив дверь C, я показал вам, что вероятность того, что дверь B скрывает приз, равна 2 из 3.'"
Вос Савант предполагает, что решение будет более интуитивным с 1 000 000 дверей, а не с 3.[3] В данном случае 999 999 дверей с козлами за ними и одна дверь с призом. После того, как игрок выбирает дверь, ведущий открывает 999 998 оставшихся дверей. В среднем, в 999 999 раз из 1 000 000 оставшаяся дверь будет содержать приз. Интуитивно игрок должен спросить, насколько вероятно, что, учитывая миллион дверей, ему или ей удалось изначально выбрать правильную. Stibel и другие[18] предположил, что потребность в рабочей памяти облагается налогом во время задачи Монти Холла и что это вынуждает людей «свернуть» свой выбор на два равновероятных варианта. Они сообщают, что когда количество вариантов увеличивается до более чем 7 вариантов (7 дверей), люди склонны переключаться чаще; однако большинство участников по-прежнему неверно оценивают вероятность успеха в соотношении 50:50.
Вос Савант и фурор в СМИ
- Скотт Смит, доктор философии. Университет Флориды
[3]
Вос Савант написала в своей первой колонке о проблеме Монти Холла, что игрок должен переключиться.[3] Она получила тысячи писем от своих читателей, подавляющее большинство из которых, в том числе многие от читателей с докторской степенью, не согласились с ее ответом. В 1990–1991 годах парадоксу были посвящены еще три ее колонки в «Параде».[19] Многочисленные примеры писем читателей колонки Вос Саванта представлены и обсуждаются в Дилемма Монти Холла: когнитивная иллюзия по преимуществу.[20]
Дискуссия воспроизводилась в других местах (например, в Сесил Адамс ' "Прямой допинг газетная колонка[14]) и сообщалось в крупных газетах, таких как Нью-Йорк Таймс.[4]
Пытаясь уточнить свой ответ, она предложила игру в оболочку[8] для иллюстрации: «Вы смотрите в сторону, и я кладу горошину под одну из трех скорлупок. Затем я прошу вас ткнуть пальцем в раковину. Вероятность того, что в вашем выборе есть горошина, 1/3, согласовано? Затем я просто поднимаю пустую оболочку из оставшихся двух. Поскольку я могу (и буду) делать это независимо от того, что вы выбрали, мы не узнали ничего, что позволило бы нам пересмотреть шансы на ракушку под вашим пальцем ». Она также предложила аналогичную симуляцию с тремя игральными картами.
Вос Савант прокомментировал это, хотя некоторая путаница была вызвана немного читатели не понимали, что они должны были предположить, что ведущий всегда должен показывать козу, почти все ее многочисленные корреспонденты правильно поняли предположения о проблеме и все еще были изначально убеждены, что ответ Вос Саванта («переключение») был неправильным.
Замешательство и критика
Источники путаницы
Когда впервые сталкивается с проблемой Монти Холла, подавляющее большинство людей предполагают, что каждая дверь имеет равную вероятность, и приходят к выводу, что переключение не имеет значения.[10] Из 228 субъектов в одном исследовании только 13% решили переключиться.[21] В ее книге Сила логического мышления,[22] цитаты когнитивный психолог Массимо Пиаттелли Пальмарини: "Никакая другая статистическая головоломка не приближается так близко к тому, чтобы постоянно одурачить всех людей [и] даже нобелевские физики систематически дают неправильный ответ, и что они настаивать и готовы ругать в печати тех, кто предлагает правильный ответ ». Голуби, неоднократно сталкивающиеся с проблемой, показывают, что они быстро учатся всегда переключаться, в отличие от людей.[23]
Большинство формулировок проблемы, особенно в Журнал Parade, не соответствуют правилам реального игрового шоу [11] и не указывают полностью поведение хоста или то, что местоположение автомобиля выбрано случайным образом.[21][4][24] Краусс и Ван предполагают, что люди делают стандартные предположения, даже если они не сформулированы явно.[25]
Хотя эти проблемы имеют математическое значение, даже с учетом этих факторов почти все люди все еще думают, что каждая из двух закрытых дверей имеет равную вероятность, и приходят к выводу, что переключение не имеет значения.[10] Это предположение о «равной вероятности» - глубоко укоренившаяся интуиция.[26] Люди сильно склонны полагать, что вероятность равномерно распределяется по всему количеству неизвестных, независимо от того, есть это или нет.[27]
Проблема продолжает привлекать внимание когнитивных психологов. Типичное поведение большинства, то есть отказ от переключения, можно объяснить феноменами, известными в психологической литературе как:
- В эффект вклада,[28] в котором люди склонны переоценивать вероятность выигрыша уже выбранной - уже «принадлежащей» - двери.
- В предубеждение статус-кво,[29] в котором люди предпочитают придерживаться выбора двери, которую они уже сделали.
- Ошибки упущения или ошибки комиссионного вознаграждения,[30] в котором, при прочих равных, люди предпочитают совершать ошибки бездействием (Остаться), а не действием (Переключить).
Экспериментальные данные подтверждают, что это правдоподобные объяснения, не зависящие от вероятностной интуиции.[31][32] Другая возможность состоит в том, что интуиция людей просто имеет дело не с учебной версией задачи, а с реальной постановкой игрового шоу.[33] Существует вероятность того, что ведущий шоу обманывает, открывая другие двери, только если изначально была выбрана дверь с автомобилем. Мастер шоу, играющий обманным путем в половине случаев, изменяет шансы на победу в случае, если одному предлагается перейти на «равную вероятность».
Критика простых решений
Как уже отмечалось, большинство источников в области вероятность, в том числе многие вводные учебники по вероятности, решают проблему, показывая условные вероятности что машина находится за дверью 1, а дверь 2 1/3 и 2/3 (не 1/2 и 1/2) при условии, что участник сначала выбирает дверь 1, а ведущий открывает дверь 3; различные способы получения и понимания этого результата были приведены в предыдущих подразделах.
Среди этих источников есть несколько, которые открыто критикуют широко представленные «простые» решения, говоря, что эти решения «правильные, но ... шаткие»,[34] или не «решайте поставленную проблему»,[35] или являются «неполными»,[36] или являются «неубедительными и вводящими в заблуждение»,[37] или являются (прямо) "ложными".[38]
Саша Волох (2015) написал, что «любое объяснение, которое говорит что-то вроде« вероятность открытия двери 1 составляет 1/3, и ничто не может изменить это ... 'автоматически подозрительно: вероятности - это выражение нашего незнания мира, а новая информация может изменить степень нашего невежества ».
Некоторые говорят, что эти решения дают ответ на несколько другой вопрос - одна фраза: «вы должны объявить прежде чем дверь была открыта планируете ли вы переключиться ».[39]
Простые решения разными способами показывают, что участник, решивший переключиться, с вероятностью выиграет машину. 2/3, и, следовательно, это переключение является выигрышной стратегией, если игроку нужно заранее выбрать между «всегда переключаться» и «всегда оставаться». Однако вероятность выигрыша всегда переключение - это логически отличное понятие от вероятности выигрыша при переключении учитывая, что игрок выбрал дверь 1, а ведущий открыл дверь 3. Как говорится в одном источнике, «различие между [этими вопросами], кажется, многих сбивает с толку».[38] Тот факт, что они разные, можно показать, варьируя задачу так, чтобы эти две вероятности имели разные числовые значения. Например, предположим, что участник знает, что Монти не выбирает вторую дверь случайным образом среди всех допустимых альтернатив, а вместо этого, когда ему предоставляется возможность выбрать между двумя проигрышными дверями, Монти откроет одну справа. В этой ситуации на следующие два вопроса есть разные ответы:
- Какова вероятность выиграть машину по всегда переключение?
- Какова вероятность выигрыша машины если игрок выбрал дверь 1, а ведущий открыл дверь 3?
Ответ на первый вопрос: 2/3, как правильно показывают «простые» решения. Но ответ на второй вопрос теперь другой: условная вероятность того, что автомобиль находится за дверью 1 или дверью 2, при условии, что хозяин открыл дверь 3 (дверь справа), равна 1/2. Это связано с тем, что Монти предпочитает крайние правые двери, что означает, что он открывает дверь 3, если машина находится за дверью 1 (что изначально с вероятностью 1/3) или если машина находится за дверью 2 (тоже изначально с вероятностью 1/3). Для этого варианта два вопроса дают разные ответы. Однако до тех пор, пока начальная вероятность того, что машина окажется за каждой дверью, равна 1/3, переключение никогда не является недостатком для участника, так как условная вероятность выигрыша в результате переключения всегда не менее 1/2.[38]
В Моргане и другие,[38] четыре университетских профессора опубликовали статью в Американский статистик утверждая, что Вос Савант дал правильный совет, но неверный аргумент. Они считали, что вопрос был задан о вероятности появления машины за дверью 2. данный первоначальный выбор игрока для двери 1 и открытой двери 3, и они показали, что этот шанс находится между 1/2 и 1 в зависимости от процесса принятия решения принимающей стороной с учетом выбора. Только когда решение полностью рандомизировано, есть шанс 2/3.
В приглашенном комментарии[40] и в последующих письмах редактору[41][42][43][44] Морган и другие были поддержаны одними писателями, критиковались другими; в каждом случае ответ Моргана и другие публикуется вместе с письмом или комментарием в Американский статистик. В частности, Вос Савант энергично защищалась. Морган и другие пожаловались в своем ответе vos Savant[41] тот vos Savant все еще фактически не ответил на свою главную мысль. Позже в их ответе Хогбину и Нидждаму:[44] они действительно согласились с тем, что было естественным предположить, что хост выбирает дверь для открытия полностью случайным образом, когда у него действительно есть выбор, и, следовательно, что условная вероятность выигрыша путем переключения (т.е. условная, учитывая ситуацию, в которой находится игрок, когда он должен сделать свой выбор) имеет такую же ценность, 2/3, как безусловная вероятность выигрыша при переключении (т.е. усредненная по всем возможным ситуациям). Это равенство уже подчеркивалось Беллом (1992), который предположил, что Морган и другие'Математически сложное решение понравится только статистикам, тогда как эквивалентность условного и безусловного решений в случае симметрии интуитивно очевидна.
В литературе существуют разногласия относительно того, является ли постановка проблемы Вос Савантом, представленная в Парад журнал задает первый или второй вопрос, а значительна ли эта разница.[45] Берендс заключает, что «нужно внимательно рассмотреть вопрос, чтобы убедиться, что оба анализа верны»; что не означает, что они одинаковы.[46] Один анализ по одному вопросу, другой анализ по другому вопросу. Несколько критиков статьи Моргана и другие,[38] чьи статьи были опубликованы вместе с оригинальной статьей, критиковали авторов за изменение формулировки Вос Савант и неверное толкование ее намерений.[45] Один из участников дискуссии (Уильям Белл) счел вопросом вкуса, упоминает ли кто-нибудь прямо, что (при стандартных условиях), который Дверь открывается хостом независимо от того, нужно ли переключаться.
Среди простых решений «решение с комбинированными дверьми» наиболее близко подходит к условному решению, как мы видели при обсуждении подходов, использующих концепцию шансов и теорему Байеса. Он основан на глубоко укоренившейся интуиции, что раскрытие информации, которая уже известна, не влияет на вероятности. Но знание того, что ведущий может открыть одну из двух не выбранных дверей, чтобы показать козу, не означает, что открытие конкретной двери не повлияет на вероятность того, что машина находится за первоначально выбранной дверью. Дело в том, что хотя мы заранее знаем, что хозяин откроет дверь и покажет козу, мы не знаем который дверь он откроет. Если хост выбирает равномерно случайным образом между дверями, скрывающими козу (как в стандартной интерпретации), эта вероятность действительно остается неизменной, но если хост может выбирать между такими дверями неслучайно, то конкретная дверь, которую открывает хост раскрывает дополнительную информацию. Хозяин всегда может открыть дверь за козой и (в стандартной трактовке задачи) вероятность нахождения автомобиля за изначально выбранной дверью не меняется, но не поэтому о первом, что второе верно. Решения, основанные на утверждении, что действия хоста не могут повлиять на вероятность того, что машина находится позади первоначально выбранного, кажутся убедительными, но утверждение просто неверно, если каждый из двух вариантов хоста не является равновероятным, если у него есть выбор.[47] Следовательно, утверждение должно быть обосновано; без объяснения причин решение в лучшем случае неполное. Ответ может быть правильным, но аргументы, использованные для его оправдания, ошибочны.
Решения с использованием условной вероятности и другие решения
Приведенные выше простые решения показывают, что игрок со стратегией переключения выигрывает машину с общей вероятностью. 2/3, т.е. без учета того, какая дверь была открыта хостом.[48][49] В отличие от большинства источников в области вероятность рассчитать условные вероятности что машина находится за дверью 1, а дверь 2 1/3 и 2/3 если участник изначально выбирает дверь 1, а ведущий открывает дверь 3.[2][38][50][35][49][48][36] Решения в этом разделе рассматривают только те случаи, когда игрок выбрал дверь 1, а хозяин открыл дверь 3.
Уточнение простого решения
Если мы предположим, что хост открывает дверь наугад, когда ему предоставляется выбор, то какая дверь открывает хост не дает нам никакой информации о том, находится ли машина за дверью 1. В простых решениях мы уже наблюдали что вероятность того, что автомобиль находится за дверью 1, дверью, изначально выбранной игроком, изначально равна 1/3. Более того, хост обязательно откроет а (другая) дверь, поэтому открытие а дверь (который дверь не указана) это не меняет. 1/3 Должна быть средняя вероятность того, что автомобиль находится за дверью 1, учитывая выбранную хозяином дверь 2 и заданную хозяином дверь 3, потому что это единственные две возможности. Но эти две вероятности одинаковы. Следовательно, они оба равны 1/3.[38] Это показывает, что вероятность того, что машина находится за дверью 1, учитывая, что игрок изначально выбрал эту дверь и учитывая, что хозяин открыл дверь 3, составляет 1/3, и отсюда следует, что вероятность того, что автомобиль находится за дверью 2, учитывая, что игрок изначально выбрал дверь 1, а хозяин открыл дверь 3, составляет 2/3. Анализ также показывает, что общий уровень успеха 2/3, достигнутая всегда переключаюсь, не может быть улучшен и подчеркивает то, что уже могло быть интуитивно очевидным: выбор, стоящий перед игроком, состоит в том, что между первоначально выбранной дверью и другой дверью, оставленной закрытой хозяином, конкретные числа на этих дверях не имеют значения.
Условная вероятность прямым вычислением

По определению условная возможность выигрыша путем переключения при условии, что участник изначально выбирает дверь 1, а ведущий открывает дверь 3, представляет собой вероятность события «машина находится за дверью 2, а ведущий открывает дверь 3», деленную на вероятность «хост открывает дверь 3». Эти вероятности можно определить, используя приведенную ниже таблицу условной вероятности или эквивалентную Древо решений как показано справа.[50][49][48] Условная вероятность выигрыша при переключении равна 1/3/1/3 + 1/6, который 2/3.[2]
В приведенной ниже таблице условной вероятности показано, как 300 случаев, во всех из которых игрок изначально выбирает дверь 1, в среднем будут разделены в зависимости от местоположения машины и выбора двери, которую будет открывать хост.
| Автомобиль спрятан за дверью 3 (в среднем 100 случаев из 300) | Автомобиль спрятан за дверью 1 (в среднем 100 случаев из 300) | Автомобиль спрятан за дверью 2 (в среднем 100 случаев из 300) | |
|---|---|---|---|
| Игрок сначала выбирает Дверь 1, 300 повторений | |||
 |  |  | |
| Хост должен открыть дверь 2 (100 ящиков) | Хозяин случайным образом открывает дверь 2 (в среднем 50 случаев) | Хозяин случайным образом открывает дверь 3 (в среднем 50 случаев) | Хост должен открыть дверь 3 (100 ящиков) |
 |  |  |  |
| Вероятность 1/3 (100 из 300) | Вероятность 1/6 (50 из 300) | Вероятность 1/6 (50 из 300) | Вероятность 1/3 (100 из 300) |
| Переключение побед | Переключение проигрывает | Переключение проигрывает | Переключение побед |
| В тех случаях, когда ведущий открывает Дверь 2, переключение побеждает в два раза чаще, чем остается (100 случаев против 50) | В тех случаях, когда ведущий открывает дверь 3, переключение побеждает в два раза чаще, чем остается (100 случаев против 50) | ||
Теорема Байеса
Многие учебники по вероятности и статьи в области теории вероятностей выводят решение с условной вероятностью посредством формального применения Теорема Байеса; среди них книги Гилла[51] и Хенце.[52] Использование шансы Форма теоремы Байеса, часто называемая правилом Байеса, делает такой вывод более прозрачным.[34][53]
Первоначально автомобиль с одинаковой вероятностью находится за любой из трех дверей: шансы на дверь 1, дверь 2 и дверь 3 равны. 1 : 1 : 1. Это остается так после того, как игрок выбрал дверь 1 по независимости. Согласно с Правило Байеса, апостериорные шансы на местонахождение машины, учитывая, что хост открывает дверь 3, равны априорным шансам, умноженным на байесовский фактор или вероятность, которая, по определению, является вероятностью новой порции информации (хост открывает дверь 3) по каждой из рассмотренных гипотез (местонахождение автомобиля). Теперь, поскольку игрок изначально выбрал дверь 1, вероятность того, что ведущий откроет дверь 3, составляет 50%, если машина находится за дверью 1, 100%, если машина находится за дверью 2, 0%, если машина находится за дверью 3. Таким образом, Фактор Байеса состоит из соотношений 1/2 : 1 : 0 или эквивалентно 1 : 2 : 0, в то время как предыдущие шансы были 1 : 1 : 1. Таким образом, апостериорные шансы становятся равными байесовскому фактору. 1 : 2 : 0. Учитывая, что хост открыл дверь 3, вероятность того, что машина находится за дверью 3, равна нулю, и это в два раза больше вероятности оказаться за дверью 2, чем за дверью 1.
Ричард Гилл[54] анализирует вероятность открытия двери 3 хостом следующим образом. Учитывая, что машина нет за дверью 1 с равной вероятностью он находится за дверью 2 или 3. Таким образом, вероятность того, что хост откроет дверь 3, составляет 50%. Учитывая, что машина является за дверью 1 вероятность того, что хост откроет дверь 3, также составляет 50%, потому что, когда у хоста есть выбор, любой из вариантов одинаково вероятен. Следовательно, независимо от того, находится ли машина за дверью 1, вероятность того, что хост откроет дверь 3, составляет 50%. Информация «хост открывает дверь 3» вносит вклад в байесовский фактор или отношение правдоподобия 1 : 1, находится ли машина за дверью 1. Первоначально вероятность того, что дверь 1 скрывает машину, была 2 : 1. Следовательно, апостериорные шансы на то, что дверь 1 скрывает машину, остаются такими же, как и предыдущие шансы, 2 : 1.
На словах информация который дверь открывается хозяином (дверь 2 или дверь 3?) не раскрывает никакой информации о том, находится ли машина за дверью 1, и это именно то, что якобы интуитивно очевидно для сторонников простых решений или использования идиомы математических доказательств, «очевидно истинные по симметрии».[43]
Прямой расчет
Рассмотрим событие Ci, указывая на то, что машина за номером двери я, принимает значение Си, для выбора игрока и значение ЗдравствуйОткрываю дверь. Первоначально игрок выбирает дверь i = 1, C = X1, и хост открывает дверь i = 3, C = H3.
В этом случае мы имеем:
P (H3 | X1) = 1/2 потому что это выражение зависит только от X1, ни на одном Ci. Итак, в этом конкретном выражении выбор хоста не зависит от того, где находится машина, и единожды остаются только две двери. X1 выбран (например, P (H1 | X1) = 0); и P (Ci, Xi) = P (Ci) P (Xi) потому что Ci и Си независимые события (игрок не знает, где машина, чтобы сделать выбор).
Затем, если игрок изначально выбирает дверь 1, а ведущий открывает дверь 3, мы доказываем, что условная вероятность выигрыша при переключении равна:
От Правило Байеса, мы знаем это P (A, B) = P (A | B) P (B) = P (B | A) P (A). Распространение этой логики на несколько событий, например А, B и C, мы получаем, что можем играть с разными подмножествами {A, B, C} для расчета вероятности пересечения, как инструмента для упрощения расчета нашей условной вероятности:
В нашем случае, поскольку мы знаем, что P (H3 | C2, X1) = 1, нам повезло:
Решение стратегического доминирования
Возвращаясь к Налебаффу,[55] проблема Монти Холла также широко изучена в литературе по теория игры и теория принятия решений, а также некоторые популярные решения соответствуют этой точке зрения. Вос Савант просит решения, а не шанса. А случайные аспекты того, как спрятана машина и как открывается незабранная дверь, неизвестны. С этой точки зрения нужно помнить, что у игрока есть две возможности сделать выбор: во-первых, какую дверь выбрать изначально; а во-вторых, переключаться или нет. Поскольку он не знает, как спрятана машина и как хозяин делает выбор, он может использовать свой первый вариант выбора, как бы нейтрализовать действия команды, проводящей викторину, включая ведущего.
Следуя за Гиллом,[56] а стратегия участника включает в себя два действия: первоначальный выбор двери и решение переключиться (или придерживаться), которое может зависеть как от изначально выбранной двери, так и от двери, на которую хост предлагает переключение. Например, стратегия одного из участников: «выбрать дверь 1, затем переключиться на дверь 2, когда предлагается, и не переключаться на дверь 3, когда предлагается». Существует двенадцать таких детерминированных стратегий участника.
Элементарное сравнение стратегий участников показывает, что для каждой стратегии A существует другая стратегия B «выбрать дверь, а затем переключиться, что бы ни случилось», которая доминирует над ней.[57] Независимо от того, как спрятана машина и какое правило использует ведущий, когда у него есть выбор между двумя козлами, если A выигрывает машину, то B также делает это. Например, в стратегии A «выбрать дверь 1, а затем всегда придерживаться ее» преобладает стратегия B «выбрать дверь 1, затем всегда переключаться после того, как хост открывает дверь»: A выигрывает, когда дверь 1 закрывает машину, а B выигрывает, когда одна из дверей 2 и 3 скрывает автомобиль. Аналогично, стратегия A «выбрать дверь 1, затем перейти на дверь 2 (если предлагается), но не переключаться на дверь 3 (если предлагается)» преобладает в стратегии B «выбрать дверь 3, затем всегда переключайтесь ".
Доминирование - веская причина для поиска решения среди стратегий постоянного переключения при довольно общих предположениях об окружающей среде, в которой участник принимает решения. В частности, если автомобиль скрыт с помощью какого-либо устройства рандомизации - например, подбрасывания симметричной или асимметричной трехсторонней матрицы - доминирование означает, что стратегия, максимизирующая вероятность выигрыша автомобиля, будет одной из трех стратегий постоянного переключения, а именно: быть стратегией, которая сначала выбирает наименее вероятную дверь, а затем переключает, независимо от того, какую дверь переключить предлагает хост.
Стратегическое господство связывает проблему Монти Холла с теория игры. в игра с нулевой суммой сеттинг Гилла[56] отказ от стратегий без переключения сводит игру к следующему простому варианту: ведущий (или телекомпания) решает, через какую дверь спрятать машину, а участник выбирает две двери (т.е. две двери, оставшиеся после первой попытки игрока). , номинальный, выбор). Участница побеждает (а ее противник проигрывает), если машина находится за одной из двух дверей, которые она выбрала.
Решения путем моделирования

Простой способ продемонстрировать, что стратегия переключения действительно выигрывает два из трех раз при стандартных предположениях, - смоделировать игру с помощью играя в карты.[58][59] Три карты из обычной колоды используются для обозначения трех дверей; одна «особая» карта представляет дверь с автомобилем, а две другие карты представляют собой козьи двери.
Моделирование можно повторить несколько раз для моделирования нескольких раундов игры. Игрок выбирает одну из трех карт, затем, глядя на оставшиеся две карты, «хозяин» сбрасывает карту козла. Если карта, остающаяся в руке хозяина, является картой автомобиля, это фиксируется как выигрыш переключения; если хозяин держит карту козла, раунд записывается как оставшаяся победа. Поскольку этот эксперимент повторяется в течение нескольких раундов, наблюдаемый процент выигрышей для каждой стратегии, вероятно, будет приблизительно соответствовать ее теоретической вероятности выигрыша в соответствии с закон больших чисел.
Повторяющиеся игры также проясняют, почему переключение - лучшая стратегия. После того, как игрок выбрал свою карту, она уже определено выиграет ли переключение раунд для игрока. Если это не убедительно, моделирование можно проводить со всей колодой.[58][14] В этом варианте карта машины отправляется хосту 51 раз из 52 и остается у хоста независимо от того, сколько раз. неКарты -машины сбрасываются.
Варианты
Распространенный вариант проблемы, принятый несколькими академическими авторами в качестве канонический проблема, не делает упрощающего предположения, что хост должен единообразно выбирать дверь для открытия, но вместо этого он использует другие стратегия. Путаница в отношении того, какая формализация является авторитетной, привела к значительной резкости, особенно потому, что этот вариант делает доказательства более сложными, не меняя оптимальности стратегии постоянного переключения для игрока. В этом варианте у игрока могут быть разные вероятности выигрыша. в зависимости от наблюдаемого выбора хоста, но в любом случае вероятность выигрыша при переключении не менее 1/2 (и может достигать 1), а общая вероятность выигрыша переключением по-прежнему точно 2/3. Варианты иногда последовательно представлены в учебниках и статьях, предназначенных для обучения основам теория вероятности и теория игры. Изучено также значительное количество других обобщений.
Другое поведение хоста
Версия проблемы Монти Холла, опубликованная в Парад в 1990 году специально не говорилось, что хозяин всегда будет открывать другую дверь, или всегда предлагал переключиться, или даже никогда не открывал дверь, обнаруживая машину. Однако Вос Савант ясно дала понять в своей второй последующей колонке, что поведение предполагаемого хозяина могло быть только тем, что привело к 2/3 вероятность, которую она дала в качестве своего первоначального ответа. «Все остальное - другой вопрос».[5] «Практически все мои критики понимали предполагаемый сценарий. Я лично прочитал почти три тысячи писем (из многих дополнительных тысяч, которые пришли) и обнаружил, что почти все настаивают на том, что, поскольку осталось два варианта (или эквивалентная ошибка), шансы были Даже. Очень немногие вызвали вопросы о двусмысленности, и письма, фактически опубликованные в колонке, не были среди этих немногих ".[60] Ответ следует, если машина случайным образом помещается за любой дверью, ведущий должен открыть дверь, в которой видна коза, независимо от первоначального выбора игрока, и, если две двери доступны, выбирает, какую из них открыть случайным образом.[10] В таблице ниже представлены различные Другой возможное поведение хоста и влияние на успех переключения.
Определение лучшей стратегии игрока в рамках данного набора других правил, которым должен следовать хост, - это тип проблемы, изучаемой в теория игры. Например, если хост не обязан делать предложение о переключении, игрок может подозревать, что хост является злонамеренным, и делает предложения чаще, если игрок изначально выбрал автомобиль. В общем, ответ на такой вопрос зависит от конкретных предположений, сделанных о поведении хоста, и может варьироваться от «полностью игнорировать хост» до «подбросить монетку и переключиться, если он выпадает орлом»; см. последнюю строку таблицы ниже.
Морган и другие[38] и Гиллман[35] оба показывают более общее решение, в котором автомобиль (равномерно) размещается случайным образом, но хост не ограничен случайным выбором равномерно, если игрок изначально выбрал автомобиль, как они оба интерпретируют формулировку проблемы в Парад несмотря на заявления автора. Оба изменили формулировку Парад версия, чтобы подчеркнуть этот момент, когда они переформулировали проблему. Они рассматривают сценарий, в котором хозяин выбирает между открытием двух коз с предпочтением, выраженным как вероятность q, имеющий значение от 0 до 1. Если хост выбирает случайным образом q было бы 1/2 и переключение выигрышей с вероятностью 2/3 независимо от того, какую дверь открывает хозяин. Если игрок выбирает дверь 1, а хозяин предпочитает дверь 3 q, то вероятность того, что хост откроет дверь 3, а машина окажется за дверью 2, равна 1/3 а вероятность того, что хозяин откроет дверь 3, а машина окажется за дверью 1, равна q/3. Это единственные случаи, когда хост открывает дверь 3, поэтому условная вероятность выигрыша при переключении учитывая, что хозяин открывает дверь 3 является 1/3/1/3 + q/3 что упрощает 1/1 + q. С q может варьироваться от 0 до 1, эта условная вероятность может варьироваться от 1/2 и 1. Это означает, что даже без ограничения хоста на выбор случайным образом, если игрок изначально выбирает машину, переключение игрока никогда не будет хуже. Однако ни один из источников не предполагает, что игрок знает, какова ценность q значит, игрок не может приписать вероятность, отличную от 2/3 это предположение Вос Савант было неявным.
| Возможное поведение хоста при неустановленной проблеме | |
|---|---|
| Поведение хозяина | Результат |
| Хост действует, как указано в конкретной версии проблемы. | В двух третях случаев автомобиль выигрывает за счет переключения. (Частный случай приведенной ниже обобщенной формы с п = q = 1/2) |
| Ведущий всегда показывает козу и всегда предлагает рубильник. Если у него есть выбор, он с вероятностью выберет крайнего левого козла. п (что может зависеть от первоначального выбора игрока) и крайняя правая дверь с вероятностью q = 1 − п.[38][34][53] | Если хозяин открывает крайнюю правую дверь, переключение выигрывает с вероятностью 1 / (1+q). |
| «Монти из ада»: ведущий предлагает возможность переключиться только тогда, когда первоначальный выбор игрока - победная дверь.[4] | Переключение всегда дает козу. |
| «Читающий мысли Монти»: хозяин предлагает возможность переключиться, если гость все равно намерен остаться или если гость переключится на козу.[33] | Переключение всегда дает козу. |
| «Ангельский Монти»: ведущий предлагает возможность переключиться только в том случае, если игрок сделал неправильный выбор.[61] | Переключение всегда побеждает машину. |
| «Монти Фолл» или «Невежественный Монти»: ведущий не знает, что находится за дверьми, и открывает одну наугад, но не обнаруживает машину.[62][34][53] | В половине случаев переключение выигрывает у машины. |
| Ведущий знает, что скрывается за дверьми, и (перед выбором игрока) наугад выбирает, какого козла показать. Он предлагает возможность переключиться только тогда, когда выбор игрока отличается от его. | В половине случаев переключение выигрывает у машины. |
| Ведущий открывает дверь и предлагает переключиться в 100% случаев, если участник изначально выбрал машину, и в 50% случаев в противном случае.[10] | Переключение побед 1/2 время в равновесие по Нэшу. |
| Четырехэтапная теоретико-игровая игра для двух игроков.[63][56] Игрок играет против организаторов шоу (телекомпании), в состав которых входит ведущий. Первый этап: организаторы выбирают дверь (выбор держится в секрете от игрока). Второй этап: игрок делает предварительный выбор двери. Третий этап: хозяин открывает дверь. Четвертый этап: игрок делает окончательный выбор. Игрок хочет выиграть машину, телеканал хочет ее оставить. Это игра для двух человек с нулевой суммой. По теореме фон Неймана из теория игры, если мы разрешаем обеим сторонам полностью рандомизированные стратегии, существует минимаксное решение или равновесие по Нэшу.[10] | Минимаксное решение (равновесие по Нэшу ): сначала машина спрятана равномерно и случайным образом, а затем хозяин выбирает одинаковую случайную дверь, чтобы открыть ее, не показывая машину и отличную от двери игрока; игрок сначала выбирает одинаковую случайную дверь, а затем всегда переключается на другую закрытую дверь. Благодаря своей стратегии у игрока есть шанс на победу не менее 2/3, однако телеканал играет; со стратегией телеканала, телеканал проиграет с вероятностью не более 2/3, однако игрок играет. Тот факт, что эти две стратегии совпадают (по крайней мере, 2/3, в большинстве 2/3) доказывает, что они образуют минимаксное решение. |
| Как и раньше, но теперь у хозяина есть возможность вообще не открывать дверь. | Минимаксное решение (равновесие по Нэшу ): машина сначала спрятана равномерно наугад, а потом хозяин никогда не открывает дверь; игрок сначала выбирает дверь равномерно и случайно, а затем никогда не переключается. Стратегия игрока гарантирует шанс на победу не менее 1/3. Стратегия телеканала гарантирует потерю не более чем 1/3. |
| Сделка или нет Случай: ведущий просит игрока открыть дверь, затем предлагает выключатель на случай, если автомобиль не обнаружен. | В половине случаев переключение выигрывает у машины. |
N двери
Д. Л. Фергюсон (1975 г. в письме к Селвину[2]) предлагает N-дверное обобщение исходной задачи, в которой открывается хост п теряет двери, а затем предлагает игроку возможность переключиться; в этом варианте с вероятностью выигрывает переключение . Эта вероятность всегда больше, чем , поэтому переключение всегда дает преимущество.
Даже если хозяин открывает только одну дверь () плеер лучше выключать в любом случае. В качестве N растет, преимущество уменьшается и приближается к нулю.[64]С другой стороны, если хост открывает все проигрывающие двери, кроме одной (п = N - 2) преимущество увеличивается как N растет (вероятность выигрыша при переключении равна N − 1/N, который приближается к 1 при N становится очень большим).
Квантовая версия
Квантовая версия парадокса иллюстрирует некоторые моменты о связи между классической или неквантовой информацией и квантовая информация, закодированные в состояниях квантово-механических систем. Формулировка в общих чертах основана на квантовая теория игр. Три двери заменены квантовой системой, допускающей три альтернативы; открыть дверь и заглянуть за нее, что переводится как выполнение определенного измерения. Правила могут быть сформулированы на этом языке, и снова игрок может выбрать исходный вариант или перейти к другому «ортогональному» варианту. Последняя стратегия, как и в классическом случае, увеличивает шансы вдвое. Однако, если ведущий шоу не рандомизировал положение приза полностью квантово-механическим способом, игрок может добиться еще большего, а иногда даже может выиграть приз с уверенностью.[65][66]
История
Самая ранняя из нескольких вероятностных головоломок, связанных с проблемой Монти Холла, - это Парадокс коробки Бертрана, поставленный Джозеф Бертран в 1889 г. Calcul des probabilités.[67] В этой головоломке есть три коробки: коробка с двумя золотыми монетами, коробка с двумя серебряными монетами и коробка с одной из каждой. После случайного выбора коробки и случайного извлечения одной монеты, которая оказывается золотой, возникает вопрос, какова вероятность того, что другая монета будет золотой. Как и в случае с проблемой Монти Холла, интуитивный ответ таков: 1/2, но на самом деле вероятность 2/3.
В Проблема трех узников, опубликовано в Мартин Гарднер с Математические игры столбец в Scientific American в 1959 г. [7][58] эквивалентна проблеме Монти Холла. Эта проблема касается трех осужденных заключенных, случайным образом один из которых был тайно выбран для помилования. Один из заключенных умоляет надзирателя назвать ему имя одного из других, который будет казнен, утверждая, что это не раскрывает никакой информации о его собственной судьбе, но увеличивает его шансы на помилование. 1/3 к 1/2. Надзиратель обязывает (тайно) подбрасывая монетку решить, какое имя назвать, если заключенный, который спрашивает, помилован. Вопрос в том, изменяет ли знание ответа надзирателя шансы заключенного на помилование. Эта проблема эквивалентна проблеме Монти Холла; у заключенного, задающего вопрос, все еще есть 1/3 шанс на помилование, но у его неназванного коллеги есть 2/3 шанс.
Стив Селвин сформулировал проблему Монти Холла в двух письмах к Американский статистик в 1975 г.[1][2] В первом письме проблема была представлена в версии, близкой к ее изложению в Парад 15 лет спустя. Второе, по-видимому, первое употребление термина «проблема Монти Холла». Проблема на самом деле в экстраполяции игрового шоу. Монти Холл сделал открывать не ту дверь, чтобы вызвать волнение, но предлагал известный меньший приз - например, 100 долларов наличными - вместо того, чтобы сменить дверь. В качестве Монти Холл написал Селвину:
И если вы когда-нибудь попадете на мое шоу, правила будут для вас неизменными - никаких торговых ящиков после выбора.
— Монти Холл[68]
Версия проблемы очень похожа на ту, которая появилась тремя годами позже в Парад была опубликована в 1987 году в разделе «Пазлы» Журнал экономических перспектив. Налебафф, как и более поздние авторы математической экономики, рассматривает эту проблему как простое и забавное упражнение. теория игры.[55]
«Ловушка Монти Холла», статья Филиппа Мартина в 1989 г. Мост сегодня, представил проблему Селвина как пример того, что Мартин называет вероятностной ловушкой, когда обрабатывает неслучайную информацию, как если бы она была случайной, и связывает это с концепциями игры в бридж.[69]
Новая версия проблемы Селвина появилась в Мэрилин Вос Савант с Спросите Мэрилин столбец вопросов и ответов Парад в сентябре 1990 г.[3] Хотя Вос Савант дал правильный ответ, что переход выиграет в двух третях случаев, по ее оценкам, журнал получил 10 000 писем, в том числе около 1000 подписанных докторами наук, многие из которых были написаны на бланках математических и научных факультетов, в которых говорилось, что ее решение было неправильным.[4] Из-за подавляющего отклика, Парад опубликовал беспрецедентные четыре колонки по этой проблеме.[70] В результате огласки проблема получила альтернативное название Мэрилин и Козы.
В ноябре 1990 года, в равной степени спорного обсуждение статьи вос Савант состоялось в Сесил Адамс столбец "Прямой допинг ".[14] Первоначально Адамс ответил неверно, что вероятность открытия двух оставшихся дверей должна быть одна к двум. После того, как читатель написал, чтобы исправить математические данные анализа Адамса, Адамс согласился, что математически он был неправ. «Вы выбираете дверь №1. Теперь вам предлагается выбор: открыть дверь №1 или открыть дверь №2 и дверь №3. В последнем случае вы сохраняете приз, если он находится за любой из дверей. Вы бы предпочли два из трех шансов получить приз, чем один из трех, не так ли? Если подумать, исходная задача предлагает вам в основном тот же выбор. По сути, Монти говорит: вы можете оставить себе одну дверь или у вас могут быть две другие двери, одну из которых (дверь без приза) я открою для вас ». Адамс сказал Парад Версия оставила критические ограничения неустановленными, и без этих ограничений шансы на победу при переключении не обязательно были двумя из трех (например, было неразумно предполагать, что хост всегда открывает дверь). Однако многочисленные читатели писали, что Адамс был «прав с первого раза» и что правильные шансы были равны одному из двух.
В Парад колонка и ее отклик получили значительное внимание в прессе, включая статью на первой полосе Нью-Йорк Таймс в котором Монти Холл сам был проинтервьюирован.[4] Холл понял проблему, продемонстрировав репортеру демонстрацию с ключами от машины и объяснив, как проходит настоящая игра. Давайте сделаем сделку отличается от правил головоломки. В статье Холл указал, что, поскольку он контролировал ход игры, играя на психологии соперника, теоретическое решение не применимо к фактическому игровому процессу шоу. Он сказал, что его не удивило утверждение экспертов о том, что вероятность была 1 из 2. «Это то же самое предположение, которое участники конкурса сделали бы на шоу после того, как я показал им, что за одной дверью ничего нет», - сказал он. «Они думали, что шансы на их дверь теперь увеличились до 1 к 2, поэтому они не хотели отказываться от двери, независимо от того, сколько денег я предлагал. Открывая эту дверь, мы оказывали давление. Мы назвали это Генри Джеймс лечение. Это было 'Поворот винта. '"Холл пояснил, что как ведущий игрового шоу ему не нужно было следовать правилам головоломки в колонке vos Savant и не всегда нужно было давать человеку возможность переключиться (например, он мог немедленно открыть дверь, если это была проигрышная дверь, может предложить им деньги, чтобы не переключиться с проигрышной двери на выигрышную, или может дать им возможность переключиться только в том случае, если у них есть выигрышная дверь). «Если хозяин должен открыть дверь, все время и предложить вам переключатель, тогда вы должны взять переключатель, - сказал он. - Но если у него есть выбор, разрешить переключение или нет, будьте осторожны. Пусть покупатель будет бдителен. Все зависит от его настроения ".
Смотрите также
- Разрушители легенд Серия 177 «Колесо мифов» - Выбери дверь
- Принцип ограниченного выбора - аналогичное применение байесовского обновления в контрактный мост
Похожие загадки в теории вероятностей и решений
Рекомендации
- ^ а б c d е Селвин 1975a.
- ^ а б c d е ж Селвин 1975b.
- ^ а б c d е ж грамм vos Savant 1990a.
- ^ а б c d е ж Тирни 1991.
- ^ а б c vos Savant 1991a.
- ^ Вазсоний 1999.
- ^ а б Гарднер 1959a.
- ^ а б Гарднер 1982.
- ^ Уитакер 1990, как цитирует vos Savant 1990a
- ^ а б c d е ж Муэзер и Гранберг, 1999 г..
- ^ а б Краусс и Ван 2003, п. 9.
- ^ vos Savant 1990b.
- ^ Карлтон 2005 заключительные замечания
- ^ а б c d е Адамс 1990.
- ^ а б Девлин 2003.
- ^ Девлин 2005.
- ^ Уильямс 2004.
- ^ а б Стибел, Дрор и Бен-Зеев 2008.
- ^ вос Савант 2012.
- ^ Гранберг 2014.
- ^ а б Гранберг и Браун 1995.
- ^ vos Savant 1996, п. 15.
- ^ Хербрэнсон и Шредер 2010.
- ^ VerBruggen 2015.
- ^ Краусс и Ван, 2003 г., п. 10.
- ^ Фальк 1992, п. 202.
- ^ Фокс и Левав 2004, п. 637.
- ^ Канеман, Knetsch & Thaler 1991.
- ^ Самуэльсон и Зекхаузер 1988.
- ^ Гилович, Медвец и Чен 1995.
- ^ Кайванто, Кролл и Забински 2014.
- ^ Morone & Fiore 2007.
- ^ а б Энслин и Вестеркамп 2018.
- ^ а б c d Розенталь 2005a.
- ^ а б c Гиллман 1992.
- ^ а б Лукас, Розенхаус и Шеплер, 2009 г..
- ^ Эйзенхауэр 2001.
- ^ а б c d е ж грамм час я Morgan et al. 1991 г..
- ^ Гиллман 1992, курсив в оригинале
- ^ Сейманн 1991.
- ^ а б vos Savant 1991c.
- ^ Рао 1992.
- ^ а б Белл 1992.
- ^ а б Хогбин и Нидждам 2010.
- ^ а б Розенхаус 2009.
- ^ Берендс 2008.
- ^ Фальк 1992 С. 207, 213.
- ^ а б c Гринстед и Снелл 2006 С. 137–138.
- ^ а б c Карлтон 2005.
- ^ а б Чун 1991.
- ^ Гилл 2002.
- ^ Хенце 2011.
- ^ а б c Розенталь 2005b.
- ^ Гилл 2011a.
- ^ а б Налебафф 1987.
- ^ а б c Гилл 2011.
- ^ Гнедин 2011.
- ^ а б c Гарднер 1959b.
- ^ vos Savant 1996, п. 8.
- ^ vos Savant 1996.
- ^ Гранберг 1996, п. 185.
- ^ Гранберг и Браун 1995, п. 712.
- ^ Гилл 2010.
- ^ Гранберг 1996, п. 188.
- ^ Флитни и Эбботт, 2002 г..
- ^ Д'Ариано и др. 2002 г..
- ^ Барбо 1993.
- ^ Холл 1975.
- ^ Мартин 1993.
- ^ vos Savant 1996, п. XV.
Библиография
- Адамс, Сесил (2 ноября 1990 г.). "На Давайте сделаем сделкуВы выбираете дверь №1. Монти открывает дверь №2 - приза нет. Вы останетесь у двери №1 или переключитесь на №3? ". Прямой допинг. Получено 25 июля 2005.
- Барбо, Эдвард (1993). «Заблуждения, недостатки и вздор: проблема автомобиля и коз». Математический журнал колледжа. 24 (2): 149–154. Дои:10.1080/07468342.1993.11973519.
- Берендс, Эрхард (2008). Пятиминутная математика. Книжный магазин AMS. п. 57. ISBN 978-0-8218-4348-2.
- Белл, Уильям (август 1992 г.). "Комментировать Давайте сделаем сделку по Моргану и другие". Американский статистик. 46 (3): 241.
- Карлтон, Мэтью (2005). «Родословные, призы и заключенные: злоупотребление условной вероятностью». Журнал статистики образования. 13 (2). Дои:10.1080/10691898.2005.11910554. S2CID 118792491. Архивировано из оригинал на 2008-10-05. Получено 2010-05-29.
- Чун, Янг Х. (1991). «Проблема игрового шоу». ИЛИ / MS сегодня. 18 (3): 9.
- D'Ariano, G.M .; Gill, R.D .; Кейл, М .; Kuemmerer, B .; Maassen, H .; Вернер, Р. Ф. (21 февраля 2002 г.). «Квантовая проблема Монти Холла». Quant. Инф. Вычислить. 2 (5): 355–366. arXiv:Quant-ph / 0202120. Bibcode:2002квант.ч..2120D.
- Девлин, Кит (Июль – август 2003 г.). "Угол Девлина: Монти Холл". Математическая ассоциация Америки. Получено 23 июн 2014.
- Девлин, Кит (Декабрь 2005 г.). "Угол Девлина: новый взгляд на Монти Холл". Математическая ассоциация Америки. Получено 23 июн 2014.
- Эйзенхауэр, Джозеф Г. (2001). "Матрица Монти Холла" (PDF). Статистика обучения. 22 (1): 17–20. Дои:10.1111/1467-9639.00005. Архивировано из оригинал (PDF) 1 марта 2012 г.. Получено 9 июля 2012.
- Enßlin, Torsten A .; Вестеркамп, Маргрет (апрель 2018 г.).«Рациональность иррациональности в проблеме Монти Холла». Annalen der Physik. 531 (3): 1800128. arXiv:1804.04948. Bibcode:2019AnP ... 53100128E. Дои:10.1002 / andp.201800128. S2CID 56036255.
- Фальк, Рума (1992). «Более пристальный взгляд на вероятности пресловутых трех заключенных». Познание. 43 (3): 197–223. Дои:10.1016/0010-0277(92)90012-7. PMID 1643813. S2CID 39617738.
- Флитни, Адриан П. и Эбботт, Дерек (2002). «Квантовая версия проблемы Монти Холла». Физический обзор A. 65 (6): 062318. arXiv:Quant-ph / 0109035. Bibcode:2002PhRvA..65f2318F. Дои:10.1103 / PhysRevA.65.062318. S2CID 119417490. Изобразительное искусство. № 062318, 2002 г.
- Фокс, Крейг Р. и Левав, Джонатан (2004). «Разделение-Редактирование-Количество: наивное экстенсиональное рассуждение при оценке условной вероятности» (PDF). Журнал экспериментальной психологии: Общие. 133 (4): 626–642. Дои:10.1037/0096-3445.133.4.626. PMID 15584810.
- Гарднер, Мартин (Октябрь 1959а). «Математические игры». Scientific American: 180–182. Перепечатано в Вторая книга журнала Scientific American по математическим головоломкам и решениям
- Гарднер, Мартин (ноябрь 1959b). «Математические игры». Scientific American: 188.
- Гарднер, Мартин (1982). Ага! Попался: парадоксы к загадкам и восторгу. В. Х. Фриман. ISBN 978-0716713616.
- Гилл, Джефф (2002). Байесовские методы. CRC Press. С. 8–10. ISBN 1-58488-288-3. (ограниченная онлайн-копия , п. 8, в Google Книги )
- Джилл, Ричард (2010). «Проблема Монти Холла». Международная энциклопедия статистической науки. Springer. С. 858–863. arXiv:1002.3878v2.
- Гилл, Ричард (февраль 2011 г.). «Проблема Монти Холла не является вероятностной головоломкой (это задача математического моделирования)». Statistica Neerlandica. 65 (1): 58–71. arXiv:1002.0651v3. Дои:10.1111 / j.1467-9574.2010.00474.x.
- Гилл, Ричард (17 марта 2011a). "Проблема Монти Холла" (PDF). Математический институт Лейденского университета, Нидерланды. С. 10–13.
- Гиллман, Леонард (1992). «Автомобиль и козы». Американский математический ежемесячный журнал. 99 (1): 3–7. Дои:10.2307/2324540. JSTOR 2324540.
- Гилович, Т .; Медвец, В. Х. и Чен, С. (1995). "Комиссионные, упущения и уменьшение диссонанса: как справиться с сожалением в проблеме" Монти Холла ". Журнал личности и социальной психологии. 21 (2): 182–190. Дои:10.1177/0146167295212008. S2CID 146500989.
- Гнедин, Саша (2011). "Игра Mondee Gills". Математический интеллект. 34: 34–41. Дои:10.1007 / s00283-011-9253-0.
- Гранберг, Дональд (2014). Дилемма Монти Холла: когнитивная иллюзия по преимуществу. Lumad / CreateSpace. ISBN 978-0996100809.
- Гранберг, Дональд (1996). «Переключаться или не переключаться». In vos Savant, Мэрилин (ред.). Сила логического мышления. Пресса Св. Мартина. ISBN 0-312-30463-3. (ограниченная онлайн-копия , п. 169, в Google Книги )
- Гранберг, Дональд и Браун, Тад А. (1995). "Дилемма Монти Холла". Бюллетень личности и социальной психологии. 21 (7): 711–729. Дои:10.1177/0146167295217006. S2CID 146329922.
- Гринстед, Чарльз М. и Снелл, Дж. Лори (4 июля 2006 г.). Введение в вероятность Гринстеда и Снелла (PDF). Получено 2 апреля 2008.
- Холл, Монти (1975). "Проблема Монти Холла". LetsMakeADeal.com. Получено 15 января 2007. Включает письмо Стиву Селвину от 12 мая 1975 г.
- Хенце, Норберт (2011) [1997]. Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls (9-е изд.). Springer. С. 50–51, 105–107. ISBN 9783834818454. (ограниченная онлайн-копия, п. 105, в Google Книги )
- Хербрэнсон, У. Т. и Шредер, Дж. (2010). «Птицы умнее математиков? Голуби (Columba Livia) оптимально работать с версией дилеммы Монти Холла ". Журнал сравнительной психологии. 124 (1): 1–13. Дои:10.1037 / a0017703. ЧВК 3086893. PMID 20175592.
- Hogbin, M .; Нидждам, В. (2010). "Письмо редактору по Давайте сделаем сделку по Моргану и другие". Американский статистик. 64 (2): 193. Дои:10.1198 / вкус.2010.09227. S2CID 219595003.
- Канеман, Д.; Knetsch, J. L. & Thaler, R.H. (1991). «Аномалии: эффект эндаумента, неприятие потерь и предубеждение статус-кво». Журнал экономических перспектив. 5: 193–206. Дои:10.1257 / jep.5.1.193.
- Kaivanto, K .; Кролл, Э. Б. и Забински, М. (2014). «Манипуляции с триггером смещения и понимание формы задачи в Монти Холле» (PDF). Бюллетень экономики. 34 (1): 89–98.
- Краусс, Стефан и Ван, X. Т. (2003). "Психология проблемы Монти Холла: открытие психологических механизмов для решения цепкой головоломки" (PDF). Журнал экспериментальной психологии: Общие. 132 (1): 3–22. Дои:10.1037/0096-3445.132.1.3. Получено 30 марта, 2008.
- Лукас, Стивен; Розенхаус, Джейсон и Шеплер, Эндрю (2009). "Проблема Монти Холла, пересмотренная" (PDF). Математический журнал. 82 (5): 332–342. Дои:10.4169 / 002557009X478355. Получено 9 июля, 2012.
- Мартин, Филлип (1993) [1989]. Грановеттер, Памела; Грановеттер, Мэтью (ред.). Ловушка Монти Холла. Только для экспертов. Книги Грановеттера.
- Morgan, J. P .; Chaganty, N.R .; Дахия, Р. К. и Довяк, М. Дж. (1991). «Давайте заключим сделку: дилемма игрока». Американский статистик. 45 (4): 284–287. Дои:10.1080/00031305.1991.10475821. JSTOR 2684453.
- Морон, А., Фиоре, А. (2007). "Три двери Монти Холла для чайников". Dipartimento di Scienze Economiche e Metodi Matematici - Università di Bari, Исследования экономики Южной Европы в области экономических исследований - S.E.R.I.E.S. Рабочий документ № 0012.
- Муэзер, Питер Р. и Гранберг, Дональд (май 1999 г.). «Новый взгляд на дилемму Монти Холла: понимание взаимосвязи определения проблемы и принятия решений». Экспериментальный. Университетская библиотека Мюнхена. Рабочий документ 99–06. Получено 10 июн 2010.
- Налебафф, Барри (Осень 1987 г.). «Головоломки: выберите занавес, дуэль, двухточечные преобразования и многое другое». Журнал экономических перспектив. 1 (2): 157–163. Дои:10.1257 / jep.1.2.157.
- Рао, М. Бхаскара (август 1992 г.). "Комментировать Давайте сделаем сделку по Моргану и другие". Американский статистик. 46 (3): 241–242.
- Розенхаус, Джейсон (2009). Проблема Монти Холла. Издательство Оксфордского университета. ISBN 978-0-19-536789-8.
- Розенталь, Джеффри С. (сентябрь 2005a). «Монти Холл, Монти Фолл, Монти Крол» (PDF). Математические горизонты: 5–7.
- Розенталь, Джеффри С. (2005b). Удар молнии: любопытный мир вероятностей. Харпер Коллинз. ISBN 978-0-00-200791-7.
- Самуэльсон, В. и Зекхаузер, Р. (1988). «Предвзятость статус-кво в принятии решений». Журнал рисков и неопределенностей. 1: 7–59. CiteSeerX 10.1.1.632.3193. Дои:10.1007 / bf00055564. S2CID 5641133.
- Селвин, Стив (февраль 1975a). «Проблема в вероятности (письмо в редакцию)». Американский статистик. 29 (1): 67–71. Дои:10.1080/00031305.1975.10479121. JSTOR 2683689.
- Селвин, Стив (август 1975b). «О проблеме Монти Холла (письмо в редакцию)». Американский статистик. 29 (3): 134. JSTOR 2683443.
- Сейманн, Р. Г. (1991). "Комментировать Давайте сделаем сделку: Дилемма игрока ». Американский статистик. 45 (4): 287–288. Дои:10.2307/2684454. JSTOR 2684454.
- Стибел, Джеффри; Дрор, Итиэль; Бен-Зеев, Талия (2008). "Теория коллапсирующего выбора: разделение выбора и суждения при принятии решений" (PDF). Теория и решение.
- Тирни, Джон (21 июля 1991 г.). «За дверями Монти Холла: загадка, дебаты и ответы?». Нью-Йорк Таймс. Получено 18 января 2008.
- Вазсоний, Андрей (декабрь 1998 г. - январь 1999 г.). "В какой двери Кадиллак?" (PDF). Линия решения: 17–19. Архивировано из оригинал (PDF) на 2014-04-13. Получено 16 октября 2012.CS1 maint: дата и год (ссылка на сайт)
- ВерБругген, Роберт (24 февраля 2015 г.). «Проблема Монти Холла: все ошибаются». RealClearScience. Получено 2017-10-12.
- Волох, Саша (02.03.2015). «Легкий ответ на печально известную проблему Монти Холла». Вашингтон Пост. ISSN 0190-8286. Получено 2017-10-12.
- Вос Савант, Мэрилин (2012) [1990–1991]. "Проблема с игровым шоу". Парад. Архивировано из оригинал 29 апреля 2012 г.
- Вос Савант, Мэрилин (9 сентября 1990a). "Спросите Мэрилин". Парад: 16. Архивировано из оригинал 21 января 2013 г.. Получено 12 ноября 2012.
- Вос Савант, Мэрилин (2 декабря 1990b). "Спросите Мэрилин". Парад: 25. Архивировано из оригинал 21 января 2013 г.. Получено 12 ноября 2012.
- Вос Савант, Мэрилин (17 февраля 1991a). "Спросите Мэрилин". Парад: 12. Архивировано из оригинал 21 января 2013 г.. Получено 12 ноября 2012.
- Вос Савант, Мэрилин (ноябрь 1991c). «Ответ Мэрилин вос Савант». Письма в редакцию. Американский статистик. 45 (4): 347.
- Вос Савант, Мэрилин (1996). Сила логического мышления. Пресса Св. Мартина. п.5. ISBN 0-312-15627-8.
- Уильямс, Ричард (2004). "Приложение D: Противоречие Монти Холла" (PDF). Заметки к курсу социологии Graduate Statistics I. Получено 2008-04-25.
- Уитакер, Крейг Ф. (9 сентября 1990 г.). «[Формулировка вопроса Мэрилин вос Савант в письме Крейга Уитакера]. Спросите Мэрилин». Парад: 16.
дальнейшее чтение
- Гилл, Ричард (2011b). "Проблема Монти Холла (версия 5)". StatProb: энциклопедия, спонсируемая обществами статистики и теории вероятностей. Архивировано из оригинал на 2016-01-21. Получено 2011-04-03.
- Вос Савант, Мэрилин (7 июля 1991b). "Спросите Мэрилин". Парад: 26. Архивировано с оригинал 21 января 2013 г.. Получено 12 ноября 2012.
- Вос Савант, Мэрилин (26 ноября 2006 г.). «Спросите Мэрилин». Парад: 6.
внешняя ссылка
- Проблема игрового шоу - исходный вопрос и ответы на веб-сайте Мэрилин вос Савант
- Калифорнийский университет в Сан-Диего, Монти знает версию и Монти не знает версию, объяснение игры
- Монти Холл в Керли
- «Палка или переключатель? Вероятность и проблема Монти Холла», Журнал BBC News, 11 сентября 2013 г. (видео). Математик Маркус дю Сотуа объясняет парадокс Монти Холла.







