Теория динамических систем - Dynamical systems theory

Теория динамических систем это область математика используется для описания поведения сложный динамические системы, обычно используя дифференциальные уравнения или же разностные уравнения. Когда используются дифференциальные уравнения, теория называется непрерывные динамические системы. С физической точки зрения непрерывные динамические системы являются обобщением классическая механика, обобщение, в котором уравнения движения постулируются напрямую и не ограничиваются Уравнения Эйлера – Лагранжа. из принцип наименьшего действия. Когда используются разностные уравнения, теория называется дискретные динамические системы. Когда временная переменная проходит через набор, который является дискретным на некоторых интервалах и непрерывным на других интервалах или является любым произвольным набором времени, таким как Кантор набор, получается динамические уравнения на временных масштабах. Некоторые ситуации также могут быть смоделированы смешанными операторами, такими как дифференциально-разностные уравнения.

Эта теория имеет дело с долгосрочным качественным поведением динамических систем и изучает природу и, если возможно, решения уравнения движения систем, которые часто в первую очередь механический или иным физическим по своей природе, например планетные орбиты и поведение электронные схемы, а также системы, возникающие в биология, экономика, и в других местах. Большая часть современных исследований сосредоточена на изучении хаотические системы.

Это направление также называют просто динамические системы, математическая теория динамических систем или математическая теория динамических систем.

В Аттрактор Лоренца является примером нелинейный динамическая система. Изучение этой системы помогло создать теория хаоса.

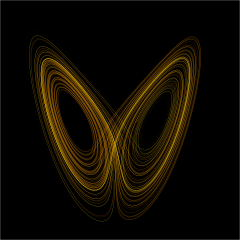
Обзор

Теория динамических систем и теория хаоса иметь дело с долгосрочным качественным поведением динамические системы. Здесь основное внимание уделяется не поиску точных решений уравнений, определяющих динамическую систему (что часто безнадежно), а, скорее, ответам на такие вопросы, как «Будет ли система стабилизироваться в долгосрочной перспективе, и если да, то какие возможны стационарные состояния? »или« Зависит ли долгосрочное поведение системы от ее начального состояния? »

Важной целью является описание неподвижных точек или стационарных состояний данной динамической системы; это значения переменной, которые не меняются со временем. Некоторые из этих неподвижных точек привлекательный, что означает, что если система запускается в соседнем состоянии, она сходится к фиксированной точке.

Точно так же интересуются периодические точки, состояния системы, которые повторяются через несколько временных шагов. Периодические точки также могут быть привлекательными. Теорема Шарковского является интересным утверждением о количестве периодических точек одномерной дискретной динамической системы.

Даже простой нелинейные динамические системы часто демонстрируют, казалось бы, случайное поведение, которое было названо хаос.^[1] Раздел динамических систем, который занимается чистым определением и исследованием хаоса, называется теория хаоса.

История

Концепция теории динамических систем берет свое начало в Ньютоновская механика. Здесь, как и в других естественных и инженерных дисциплинах, правило эволюции динамических систем неявно задается соотношением, которое дает состояние системы только на короткое время в будущем.

До появления быстрые вычислительные машины решение динамической системы требует сложных математических методов и может быть выполнено только для небольшого класса динамических систем.

Некоторые отличные презентации математической теории динамических систем включают: Бельтрами (1990) Ошибка harvtxt: нет цели: CITEREFBeltrami1990 (помощь), Люенбергер (1979), Падуло и Арбиб (1974), и Строгац (1994).^[2]

Концепции

Динамические системы

В динамическая система понятие математическое формализация для любого фиксированного «правила», которое описывает время зависимость положения точки в ее окружающее пространство. Примеры включают математические модели которые описывают качание часового маятника, течение воды в трубе и количество рыб в озере каждую весну.

Динамическая система имеет государственный определяется совокупностью действительные числа, или в более общем плане набор из точки в соответствующем пространство состояний. Небольшие изменения в состоянии системы соответствуют небольшим изменениям в числах. Цифры также являются координатами геометрического пространства - многообразие. В правило эволюции динамической системы является фиксированное правило который описывает, какие будущие состояния следуют из текущего состояния. Правило может быть детерминированный (для заданного временного интервала одно будущее состояние может быть точно предсказано с учетом текущего состояния) или стохастический (эволюцию состояния можно предсказать только с определенной вероятностью).

Динамизм

Динамизм, также называемый динамическая гипотеза или динамическая гипотеза в когнитивной науке или же динамическое познание, это новый подход в наука о мышлении на примере работы философа Тим ван Гелдер. Он утверждает, что дифференциальные уравнения больше подходят для моделирования познание чем более традиционный компьютер модели.

Нелинейная система

В математика, а нелинейная система это система, которая не линейный - т.е. система, которая не удовлетворяет принцип суперпозиции. Менее технически нелинейная система - это любая проблема, в которой переменные, которые необходимо решить, не могут быть записаны как линейная сумма независимых компонентов. А неоднородный системы, которая является линейной, если не считать наличия функции независимые переменные, является нелинейным согласно строгому определению, но такие системы обычно изучаются наряду с линейными системами, поскольку они могут быть преобразованы в линейную систему, если известно конкретное решение.

Связанные поля

Арифметическая динамика

Арифметическая динамика это область, возникшая в 1990-х годах, которая объединяет две области математики, динамические системы и теория чисел. Классически дискретная динамика относится к изучению итерация автокарт комплексная плоскость или же реальная линия. Арифметическая динамика - это изучение теоретико-числовых свойств целых, рациональных, п-адические и / или алгебраические точки при повторном применении многочлен или же рациональная функция.

Теория хаоса

Теория хаоса описывает поведение некоторых динамические системы - то есть системы, состояние которых изменяется со временем, - которые могут демонстрировать динамику, которая очень чувствительна к начальным условиям (обычно называемая эффект бабочки ). В результате этой чувствительности, проявляющейся в экспоненциальном росте возмущений начальных условий, проявляется поведение хаотических систем. случайный. Это происходит, даже если эти системы детерминированный, что означает, что их будущая динамика полностью определяется их начальными условиями без каких-либо случайных элементов. Такое поведение известно как детерминированный хаос или просто хаос.

Комплексные системы

Комплексные системы это научная область, изучающая общие свойства системы считается сложный в природа, общество, и наука. Его еще называют теория сложных систем, наука о сложности, изучение сложных систем и / или науки о сложности. Ключевыми проблемами таких систем являются трудности с их формальным моделирование и симуляция. С этой точки зрения, в различных контекстах исследования сложные системы определяются на основе их различных атрибутов.

Изучение сложных систем придает новую жизнь многим областям науки, которые более типичны. редукционист стратегия потерпела неудачу. Комплексные системы поэтому часто используется как широкий термин, охватывающий исследовательский подход к проблемам во многих различных дисциплинах, включая неврология, социальные науки, метеорология, химия, физика, Информатика, психология, искусственная жизнь, эволюционные вычисления, экономика, прогноз землетрясений, молекулярная биология и исследования в природе жизни клетки самих себя.

Теория управления

Теория управления это междисциплинарная ветвь инженерное дело и математика, частично это касается влияния на поведение динамические системы.

Эргодическая теория

Эргодическая теория это филиал математика что изучает динамические системы с инвариантная мера и связанные с этим проблемы. Его первоначальная разработка была мотивирована проблемами статистическая физика.

Функциональный анализ

Функциональный анализ это филиал математика, и в частности анализ, занимающийся изучением векторные пространства и операторы действуя на них. Его исторические корни лежат в изучении функциональные пространства, в частности, преобразования функции, такой как преобразование Фурье, а также при изучении дифференциал и интегральные уравнения. Это использование слова функциональный возвращается к вариационное исчисление, подразумевая функцию, аргумент которой является функцией. Его использование в целом приписывают математикам и физикам. Вито Вольтерра и его основание в значительной степени приписывают математику Стефан Банах.

Графические динамические системы

Концепция чего-либо графические динамические системы (GDS) можно использовать для захвата широкого спектра процессов, происходящих в графах или сетях. Основная тема математического и вычислительного анализа графических динамических систем состоит в том, чтобы связать их структурные свойства (например, сетевое соединение) и возникающую в результате глобальную динамику.

Проектируемые динамические системы

Проектируемые динамические системы это математический теория, исследующая поведение динамические системы где решения ограничены набором ограничений. Дисциплина разделяет связи и приложения с статическим миром оптимизация и равновесие проблемы и динамичный мир обыкновенные дифференциальные уравнения. Спроектированная динамическая система задается поток к проектируемому дифференциальному уравнению.

Символическая динамика

Символическая динамика практика моделирования топологического или гладкого динамическая система дискретным пространством, состоящим из бесконечных последовательности абстрактных символов, каждый из которых соответствует состоянию системы, с динамикой (эволюцией), заданной оператор смены.

Системная динамика

Системная динамика это подход к пониманию поведения систем во времени. Он имеет дело с внутренними контурами обратной связи и временными задержками, которые влияют на поведение и состояние всей системы.^[3] Что отличает использование системной динамики от других подходов к изучению систем, так это использование Обратная связь петли и запасы и потоки. Эти элементы помогают понять, как даже простые на первый взгляд системы вызывают недоумение. нелинейность.

Топологическая динамика

Топологическая динамика является разделом теории динамических систем, в котором качественные, асимптотические свойства динамических систем изучаются с точки зрения общая топология.

Приложения

В биомеханике

В спортивная биомеханика Теория динамических систем появилась в науках о движении как жизнеспособная основа для моделирования спортивных результатов и эффективности. С точки зрения динамических систем, двигательная система человека представляет собой очень сложную сеть взаимозависимых подсистем (например, дыхательную, кровеносную, нервную, скелетно-мышечную, перцепционную), которые состоят из большого количества взаимодействующих компонентов (например, клеток крови, кислорода молекулы, мышечная ткань, метаболические ферменты, соединительная ткань и кости). В теории динамических систем модели движения возникают в результате общих процессов самоорганизации, присущих физическим и биологическим системам.^[4] Нет никаких исследований, подтверждающих какие-либо утверждения, связанные с концептуальным применением этой структуры.

В когнитивной науке

Теория динамических систем применялась в области нейробиология и когнитивное развитие, особенно в неопиажеские теории когнитивного развития. Это убеждение, что когнитивное развитие лучше всего представлено физическими теориями, а не теориями, основанными на синтаксисе и AI. Также считалось, что дифференциальные уравнения являются наиболее подходящим инструментом для моделирования поведения человека. Эти уравнения интерпретируются как представление когнитивной траектории агента через пространство состояний. Другими словами, сторонники динамики утверждают, что психология должно быть (или является) описанием (посредством дифференциальных уравнений) познания и поведения агента при определенных внешних и внутренних давлениях. Также часто используется язык теории хаоса.

В нем ум ученика достигает состояния дисбаланса, когда старые шаблоны ломаются. Это фазовый переход когнитивного развития. Самоорганизация (спонтанное создание связанных форм) наступает, когда уровни активности связываются друг с другом. Новообразованные макроскопические и микроскопические структуры поддерживают друг друга, ускоряя процесс. Эти связи формируют структуру нового состояния порядка в сознании посредством процесса, называемого гребешок (повторяющееся наращивание и разрушение сложного перформанса.) Это новое, новое состояние - прогрессивное, дискретное, своеобразное и непредсказуемое.^[5]

Теория динамических систем недавно была использована для объяснения давно остававшейся без ответа проблемы в развитии детей, известной как Ошибка A-not-B.^[6]

В развитии второго языка

Применение теории динамических систем для изучения овладение вторым языком приписывается Дайан Ларсен-Фриман которая опубликовала статью в 1997 году, в которой утверждала, что овладение вторым языком следует рассматривать как процесс развития, который включает истощение языка а также овладение языком.^[7] В своей статье она утверждала, что язык следует рассматривать как динамическую систему, которая является динамической, сложной, нелинейной, хаотической, непредсказуемой, чувствительной к начальным условиям, открытой, самоорганизующейся, чувствительной к обратной связи и адаптивной.

Смотрите также

Связанные темы

Родственные ученые

Примечания

дальнейшее чтение

• Abraham, Frederick D .; Авраам, Ральф; Шоу, Кристофер Д. (1990). Визуальное введение в теорию динамических систем для психологии. Воздушный пресс. ISBN  978-0-942344-09-7. OCLC  24345312.
• Бельтрами, Эдвард Дж. (1998). Математика для динамического моделирования (2-е изд.). Академическая пресса. ISBN  978-0-12-085566-7. OCLC  36713294.
• Гайек, Отомар (1968). Динамические системы в плоскости. Академическая пресса. OCLC  343328.
• Люенбергер, Дэвид Г. (1979). Введение в динамические системы: теория, модели и приложения. Вайли. ISBN  978-0-471-02594-8. OCLC  4195122.
• Мишель, Энтони; Кайнин Ван; Бо Ху (2001). Качественная теория динамических систем. Тейлор и Фрэнсис. ISBN  978-0-8247-0526-8. OCLC  45873628.
• Падуло, Луи; Арбиб, Михаил А. (1974). Теория систем: единый подход в пространстве состояний к непрерывным и дискретным системам. Сондерс. ISBN  9780721670355. OCLC  947600.
• Строгац, Стивен Х. (1994). Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике. Эддисон Уэсли. ISBN  978-0-7382-0453-6. OCLC  49839504.

внешняя ссылка

• Динамические системы Энциклопедия когнитивной науки.
• Определение динамической системы в MathWorld.
• DSWeb Журнал Dynamical Systems