Модель Рэмси – Касса – Купманса - Ramsey–Cass–Koopmans model
В Модель Рэмси – Касса – Купманса, или же Модель роста Рамсея, это неоклассический модель экономический рост основанный прежде всего на работе Фрэнк П. Рэмси,[1] со значительными расширениями Дэвид Касс и Тьяллинг Купманс.[2][3] Модель Рэмси – Касса – Купманса отличается от модели Модель Солоу – Лебедя в этом выбор потребление явно микрооснованный в определенный момент времени и таким образом эндогенизирует норма сбережений. В результате, в отличие от модели Солоу – Свона, норма сбережений может не быть постоянной при переходе к долгосрочному периоду. устойчивое состояние. Еще одно следствие модели - результат Оптимальный по Парето или же Парето эффективный.[примечание 1]
Первоначально Рэмси представил модель как социальный планировщик проблема максимального увеличения уровня потребления в течение следующих друг за другом поколений.[4] Лишь позже Касс и Купманс приняли модель как описание децентрализованной динамичной экономики с представитель агента. Модель Рамси-Касса-Купманса направлена только на объяснение долгосрочного экономического роста, а не колебаний бизнес-цикла, и не включает никаких источников нарушений, таких как несовершенство рынка, неоднородность среди домашних хозяйств или внешние факторы. потрясения. Поэтому последующие исследователи расширили модель, допустив потрясения, связанные с государственными закупками, колебания в занятости и другие источники нарушений, известные как теория реального делового цикла.
Математическое описание
Модель Рэмси – Касса – Купманса начинается с совокупная производственная функция что удовлетворяет Условия Inada, часто указывается как Кобб – Дуглас тип, , с факторами капитала и труд . Поскольку эта производственная функция предполагается равной однородный 1 степени, можно выразить это в на душу населения термины, . Количество рабочей силы равно численности населения в экономике и растет с постоянной скоростью. , т.е. куда было население в начальный период.
Первое ключевое уравнение модели Рамсея – Касса – Купманса - это уравнение состояния для накопления капитала:
нелинейное дифференциальное уравнение, подобное Модель Солоу – Лебедя, куда является капиталоемкость (т.е. капитал на одного рабочего), сокращенно в Обозначение Ньютона для изменения капиталоемкости с течением времени, потребление на одного рабочего, выход на одного рабочего для данного , и это амортизация ставка капитала. При упрощающем предположении об отсутствии роста населения это уравнение утверждает, что вложение, или увеличение капитал на одного рабочего - это та часть продукции, которая не потребляется, за вычетом нормы износа капитала. Таким образом, инвестиции - это то же самое, что и сбережения.
Второе уравнение модели - это решение социальный планировщик проблема максимизации функция социального обеспечения, , состоящий из потока экспоненциально дисконтированный мгновенный полезность от потребления, где это учетная ставка отражающий предпочтение времени. Предполагается, что в экономике проживают идентичные люди, так что оптимальный контроль проблема может быть сформулирована в терминах бесконечно существующего представитель агента с инвариантной во времени утилитой: . Предполагается, что функция полезности строго возрастает (т. Е. Отсутствует точка блаженства ) и вогнуться , с ,[заметка 2] куда сокращенное обозначение предельная полезность потребления . Нормализация исходной популяции к одному, проблема может быть сформулирована как:
где начальный ненулевой акционерный капитал дано. Решение этой проблемы обычно находят с помощью Гамильтонова функция,[заметка 3][примечание 4] - нелинейное дифференциальное уравнение, описывающее оптимальную эволюцию потребления,
который известен как Правило Кейнса – Рамсея.[5] Период, термин , куда сокращенное обозначение предельный продукт капитала , отражает предельную доходность чистые инвестиции. Выражение отражает кривизна функции полезности; это взаимный известен как (межвременной) эластичность замещения и указывает, насколько агент-представитель желает плавное потребление через некоторое время. Часто предполагается, что эта эластичность является положительной константой, т.е. .
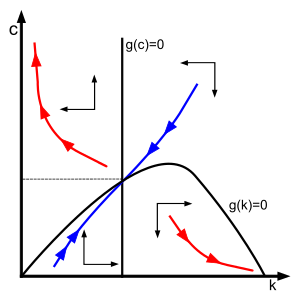
Два связанных дифференциальных уравнения для и из группы Ramsey – Cass – Koopmans динамическая система. Его устойчивое состояние, который можно найти, задав и равный нулю, задается парой неявно определяется
Качественное заявление о стабильность решения требует линеаризации первого порядка Полином Тейлора
куда это Матрица якобиана оценивается в устойчивом состоянии,[примечание 5] данный
у которого есть детерминант поскольку всегда положительный, положительно по предположению, и только отрицательно, поскольку является вогнутый. Поскольку определитель равен произведению собственные значения, собственные значения должны быть действительными и противоположными по знаку.[6] Следовательно теорема о стабильном многообразии, равновесие точка перевала и существует уникальное устойчивое плечо, или «седловой путь», который сходится к точке равновесия, обозначенной синей кривой на фазовой диаграмме. Система называется «устойчивой по седловому пути», так как все неустойчивые траектории исключаются из-за отсутствия Схема Понци " условие:[7]
подразумевая, что приведенная стоимость акционерного капитала не может быть отрицательным.[примечание 6]
История
В этом разделе несколько вопросов. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Спир и Янг пересматривают историю оптимального роста в 1950-х и 1960-х годах.[8] частично фокусируясь на правдивости заявленной одновременной и независимой разработки «Оптимального роста в агрегированной модели накопления капитала» Касса (опубликованной в 1965 г. в Обзор экономических исследований ) и «О концепции оптимального экономического роста» Тьяллинга Купмана (опубликовано в «Неделе исследований эконометрического подхода к планированию развития», 1965, Рим: Папская академия наук).
На протяжении своей жизни ни Касс, ни Купманс никогда не предполагали, что их результаты, характеризующие оптимальный рост в односекторной модели непрерывного роста, были чем-то иным, кроме «одновременного и независимого». То, что вопрос приоритета когда-либо стал предметом обсуждения, было связано только с тем, что в опубликованной версии работы Купманса он процитировал главу из тезиса Касса, которая позже стала ВИЭ бумага. В своей статье Купманс заявляет в сноске, что Касс независимо получил условия, аналогичные тем, что находит Купманс, и что Касс также рассматривает в своей статье предельный случай, когда учетная ставка стремится к нулю. Со своей стороны, Касс отмечает, что «после завершения первоначальной версии этой статьи наше внимание привлек очень похожий анализ Купманса. Мы опираемся на его результаты при обсуждении предельного случая, когда эффективная социальная ставка дисконтирования обращается к нулю» . В интервью, которое Касс дала Макроэкономическая динамика, он считает, что Купманс указал ему на предыдущую работу Фрэнка Рэмси, утверждая, что был смущен тем, что не знал о ней, но ничего не говорит, чтобы развеять основное утверждение о том, что его работа и работа Купманса фактически независимы.
Спир и Янг оспаривают эту историю, основываясь на ранее упущенной из виду рабочей версии статьи Купманса:[9] которая послужила основой для часто цитируемой презентации Купманса на конференции, проведенной Папская академия наук в октябре 1963 г.[10] В этом документе для обсуждения Cowles есть ошибка. Купманс утверждает в своем основном результате, что уравнения Эйлера являются необходимыми и достаточными для характеристики оптимальных траекторий в модели, потому что любые решения уравнений Эйлера, которые не сходятся к оптимальному установившемуся состоянию, столкнутся либо с нулевым потреблением, либо с нулевой границей капитала в конечное время. Эта ошибка, по-видимому, была представлена на конференции в Ватикане, хотя на момент ее представления Купмансом ни один из участников не прокомментировал проблему. Это можно сделать вывод, потому что обсуждение после каждой презентации доклада на конференции в Ватикане дословно сохраняется в томе конференции.
В обсуждении тома Ватикана после презентации доклада Эдмон Малинво, проблема действительно возникает из-за явного включения Малинво так называемого «условия трансверсальности» (которое Малинво называет условием I) в его статье. В конце презентации Купманс спрашивает Малинво, не так ли, что Условие I просто гарантирует, что решения уравнений Эйлера, которые не сходятся к оптимальному установившемуся состоянию, достигают границы за конечное время. Малинво отвечает, что это не так, и предлагает Купману взглянуть на пример с функциями полезности журнала и производственными функциями Кобба-Дугласа.
На этом этапе Купманс, очевидно, осознает, что у него есть проблема, но, основываясь на сбивающем с толку приложении к более поздней версии статьи, опубликованной после конференции в Ватикане, он, кажется, не может решить, как решить проблему, поднятую Условием I.
От Макроэкономическая динамика интервью с Кэсс, очевидно, что Купманс встретился с научным руководителем Касса, Хирофуми Удзава, на зимних собраниях Эконометрическое общество в январе 1964 года, когда Удзава сообщил ему, что его ученик [Касс] уже решил эту проблему. Затем Удзава, должно быть, предоставил Купмансу копию главы диссертации Касса, которую он, по-видимому, прислал под видом Технического отчета IMSSS, который Купманс цитировал в опубликованной версии своей статьи. Слово «обличие» здесь уместно, потому что номер ТУ, указанный в цитировании Купманса, указывал бы на дату выпуска отчета в начале 1950-х годов, чего явно не было.
В опубликованной версии статьи Купманса он налагает новое условие Альфа в дополнение к уравнениям Эйлера, заявляя, что единственная допустимая траектория среди тех, которые удовлетворяют уравнениям Эйлера, - это та, которая сходится к оптимальному установившемуся равновесию модели. Этот результат получен в статье Касса посредством наложения условия трансверсальности, которое Касс вывел из соответствующих разделов книги посредством Лев Понтрягин.[11] Спир и Янг предполагают, что Купманс выбрал этот путь, потому что не хотел, чтобы он «заимствовал» технологию трансверсальности Малинво или Касса.
Основываясь на этом и другом исследовании вклада Малинво в 1950-е годы - в частности, на его интуитивном понимании важности условия трансверсальности - Спир и Янг предполагают, что неоклассическую модель роста лучше назвать моделью Рамсея-Малинво-Касса, чем установленной моделью Рамсея– Почетный знак Кэсс-Купманса.
Примечания
- ^ Этот результат связан не только с эндогенностью нормы сбережений, но и с бесконечным характером горизонта планирования агентов в модели; это не выполняется в других моделях с эндогенными нормами сбережений, но более сложной межпоколенческой динамикой, например, в Самуэльсона или же Алмазов модели перекрывающихся поколений.
- ^ Предположение, что на самом деле имеет решающее значение для анализа. Если , то при малых значениях оптимальное значение равно 0 и, следовательно, если достаточно мало, существует начальный интервал времени, где даже если , видеть Нæвдал, Э. (2019). «Новые выводы из канонической модели роста Рэмси-Касса-Купманса». Макроэкономическая динамика. Дои:10.1017 / S1365100519000786.
- ^ Гамильтониан проблемы Рамси – Касса – Купманса имеет вид
- ^ Проблему также можно решить с помощью классических вариационное исчисление методы, см. Hadley, G .; Кемп, М. К. (1971). Вариационные методы в экономике. Нью-Йорк: Эльзевир. С. 50–71. ISBN 978-0-444-10097-9.
- ^ Матрица Якоби системы Рамсея – Касса – Купманса имеет вид
- ^ Можно показать, что условие «отсутствия схемы Понци» следует из условия трансверсальности гамильтониана, см. Барро, Роберт Дж.; Сала-и-Мартин, Ксавьер (2004). Экономический рост (Второе изд.). Нью-Йорк: Макгроу-Хилл. С. 91–92. ISBN 978-0-262-02553-9.
Рекомендации
- ^ Рэмси, Фрэнк П. (1928). «Математическая теория сбережений». Экономический журнал. 38 (152): 543–559. Дои:10.2307/2224098. JSTOR 2224098.
- ^ Кэсс, Дэвид (1965). «Оптимальный рост в агрегированной модели накопления капитала». Обзор экономических исследований. 32 (3): 233–240. Дои:10.2307/2295827. JSTOR 2295827.
- ^ Купманс, Т. К. (1965). «О концепции оптимального экономического роста». Экономический подход к планированию развития. Чикаго: Рэнд МакНелли. С. 225–287.
- ^ Коллард, Дэвид А. (2011). «Рэмси, спасение и поколения». Поколения экономистов. Лондон: Рутледж. С. 256–273. ISBN 978-0-415-56541-7.
- ^ Бланшар, Оливье Жан; Фишер, Стэнли (1989). Лекции по макроэкономике. Кембридж: MIT Press. С. 41–43. ISBN 978-0-262-02283-5.
- ^ Бивис, Брайан; Доббс, Ян (1990). Теория оптимизации и устойчивости для экономического анализа. Нью-Йорк: Издательство Кембриджского университета. п. 157. ISBN 978-0-521-33605-5.
- ^ Роу, Терри Л .; Смит, Родни Б. У .; Сараджоглу, Д. Сирин (2009). Мультисекторные модели роста: теория и применение. Нью-Йорк: Спрингер. п. 48. ISBN 978-0-387-77358-2.
- ^ Spear, S. E .; Янг, W. (2014). "Оптимальные сбережения и оптимальный рост: связь Касса – Малинво – Купманса". Макроэкономическая динамика. 18 (1): 215–243. Дои:10.1017 / S1365100513000291.
- ^ Купманс, Тьяллинг (декабрь 1963 г.). «О концепции оптимального экономического роста» (PDF). Документ для обсуждения Фонда Коулза 163.
- ^ Маккензи, Лайонел (2002). «Некоторые ранние конференции по теории роста». В Битросе, Джордж; Кацулакос, Яннис (ред.). Очерки экономической теории, экономического роста и рынков труда. Челтенхэм: Эдвард Элгар. С. 3–18. ISBN 978-1-84064-739-6.
- ^ Понтрягин, Лев; Болтянский, Владимир; Гамкрелидзе, Реваз; Мищенко, Евгений (1962). Математическая теория оптимальных процессов.. Нью-Йорк: Джон Вили.
дальнейшее чтение
- Аджемоглу, Дарон (2009). «Неоклассическая модель роста». Введение в современный экономический рост. Принстон: Издательство Принстонского университета. С. 287–326. ISBN 978-0-691-13292-1.
- Барро, Роберт Дж.; Сала-и-Мартин, Ксавьер (2004). «Модели роста с оптимизацией потребителей». Экономический рост (Второе изд.). Нью-Йорк: Макгроу-Хилл. С. 85–142. ISBN 978-0-262-02553-9.
- Бенасси, Жан-Паскаль (2011). "Модель Рэмси". Макроэкономическая теория. Нью-Йорк: Издательство Оксфордского университета. С. 145–160. ISBN 978-0-19-538771-1.
- Бланшар, Оливье Жан; Фишер, Стэнли (1989). «Потребление и инвестиции: основные модели бесконечного горизонта». Лекции по макроэкономике. Кембридж: MIT Press. С. 37–89. ISBN 978-0-262-02283-5.
- Мяо, Цзяньцзюнь (2014). «Неоклассические модели роста». Экономическая динамика в дискретном времени. Кембридж: MIT Press. С. 353–364. ISBN 978-0-262-02761-8.
- Новалес, Альфонсо; Фернандес, Эстер; Руис, Хесус (2009). «Оптимальный рост: непрерывный временной анализ». Экономический рост: теория и численные методы решения. Берлин: Springer. С. 101–154. ISBN 978-3-540-68665-1.
- Ромер, Дэвид (2011). «Модели бесконечного горизонта и перекрывающихся поколений». Продвинутая макроэкономика (Четвертое изд.). Нью-Йорк: Макгроу-Хилл. С. 49–77. ISBN 978-0-07-351137-5.

























![{displaystyle {dot {c}} = - {frac {u_ {c} (c)} {ccdot u_ {cc} (c)}} left [f_ {k} (k) -delta -ho ight] cdot c}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21e7f4537f8b35b3701c02477835e438563c8cc5)






















![{displaystyle H = e ^ {- ho t} u (c) + mu left [f (k) - (n + delta) k-cight]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63ca47c8d8e4ce7f389e1e11f4696fcabc803319)


![{displaystyle mathbf {J} left (k, cight) = {egin {bmatrix} {frac {partial {dot {k}}} {partial k}} & {frac {partial {dot {k}}}} {partial c} } {frac {partial {dot {c}}} {partial k}} & {frac {partial {dot {c}}} {partial c}} end {bmatrix}} = {egin {bmatrix} f_ {k} (k) - (n + delta) & - 1 {frac {1} {sigma}} f_ {kk} (k) cdot c & {frac {1} {sigma}} left [f_ {k} (k) - delta -ho ight] конец {bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7d33d5204abc754b93f17a3c5ff091f4135cdf5)