Список равномерных многогранников треугольником Шварца - List of uniform polyhedra by Schwarz triangle

Между равномерные многогранники. В Строительство Wythoff умеет строить почти все однородные многогранники из острых и тупых Треугольники Шварца. Цифры, которые можно использовать для обозначения сторон не-двугранный Острый или тупой треугольник Шварца, который не обязательно приводит только к вырожденным однородным многогранникам, - это 2, 3, 3/2, 4, 4/3, 5, 5/2, 5/3 и 5/4 (но числа с числителем 4 и те, у кого числитель 5, могут не встречаться вместе). (4/2 также можно использовать, но это приводит только к вырожденным однородным многогранникам, поскольку 4 и 2 имеют общий делитель.) Таких треугольников Шварца 44 (5 с тетраэдрическая симметрия, 7 с октаэдрическая симметрия и 32 с икосаэдрическая симметрия ), которые вместе с бесконечным семейством двугранный Треугольники Шварца могут образовывать почти все не-выродиться равномерные многогранники. Многие вырожденные однородные многогранники с полностью совпадающими вершинами, ребрами или гранями также могут быть сгенерированы конструкцией Витхоффа, а те, которые возникают из треугольников Шварца, не использующих 4/2, также приведены в таблицах ниже вместе с их невырожденными аналогами. . Треугольники Reflex Schwarz не были включены, так как они просто создают дубликаты или вырождаются; однако некоторые из них упомянуты за пределами таблиц из-за их применения к трем из курносые многогранники.
Есть несколько неоднородных многогранников, не относящихся к Витоффу, которые не могут образовать треугольники Шварца; однако большинство из них могут быть сгенерированы с использованием конструкции Витхоффа в виде двойных покрытий (многогранник, не являющийся Витхоффом, покрывается дважды, а не один раз) или с несколькими дополнительными совпадающими гранями, которые необходимо отбросить, чтобы оставить не более двух граней на каждом ребре (см. Омнитусеченный многогранник # Остальные четные невыпуклые многогранники ). Такие многогранники отмечены в этом списке звездочкой. Единственные однородные многогранники, которые все еще не могут быть порождены конструкцией Витхоффа, - это большой диромбикосододекаэдр и большой дизнуб диргомбидодекаэдр.
Каждая мозаика из треугольников Шварца на сфере может покрывать сферу только один раз, или вместо этого она может наматываться вокруг сферы целое число раз, пересекаясь в процессе. Число раз, когда мозаичный ветер оборачивается вокруг сферы, равно плотность замощения и обозначается μ.
Краткие названия многогранников Джонатана Бауэрса, известные как акронимы Бауэрса, используются вместо полных имен многогранников для экономии места. Также указан индекс Мэдера. За исключением двугранных треугольников Шварца, треугольники Шварца упорядочены по их плотности.
Треугольники Мебиуса и Шварца
Есть 4 сферических треугольника с углами π / p, π / q, π / r, где (p q r) - целые числа: (Coxeter, «Равномерные многогранники», 1954 г.)
- (2 2 р) - Двугранный
- (2 3 3) - Тетраэдр
- (2 3 4) - Октаэдрический
- (2 3 5) - Икосаэдр
Они называются треугольниками Мёбиуса.
Кроме того Треугольники Шварца рассмотрим (p q r), которые являются рациональными числами. Каждый из них может быть отнесен к одному из 4-х наборов выше.
| Плотность (μ) | Двугранный | Тетраэдр | Восьмигранный | Икосаэдр |
|---|---|---|---|---|
| d | (2 2 п/d) | |||
| 1 | (2 3 3) | (2 3 4) | (2 3 5) | |
| 2 | (3/2 3 3) | (3/2 4 4) | (3/2 5 5), (5/2 3 3) | |
| 3 | (2 3/2 3) | (2 5/2 5) | ||
| 4 | (3 4/3 4) | (3 5/3 5) | ||
| 5 | (2 3/2 3/2) | (2 3/2 4) | ||
| 6 | (3/2 3/2 3/2) | (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5) | ||
| 7 | (2 3 4/3) | (2 3 5/2) | ||
| 8 | (3/2 5/2 5) | |||
| 9 | (2 5/3 5) | |||
| 10 | (3 5/3 5/2), (3 5/4 5) | |||
| 11 | (2 3/2 4/3) | (2 3/2 5) | ||
| 13 | (2 3 5/3) | |||
| 14 | (3/2 4/3 4/3) | (3/2 5/2 5/2), (3 3 5/4) | ||
| 16 | (3 5/4 5/2) | |||
| 17 | (2 3/2 5/2) | |||
| 18 | (3/2 3 5/3), (5/3 5/3 5/2) | |||
| 19 | (2 3 5/4) | |||
| 21 | (2 5/4 5/2) | |||
| 22 | (3/2 3/2 5/2) | |||
| 23 | (2 3/2 5/3) | |||
| 26 | (3/2 5/3 5/3) | |||
| 27 | (2 5/4 5/3) | |||
| 29 | (2 3/2 5/4) | |||
| 32 | (3/2 5/4 5/3) | |||
| 34 | (3/2 3/2 5/4) | |||
| 38 | (3/2 5/4 5/4) | |||
| 42 | (5/4 5/4 5/4) |
Хотя многогранник обычно имеет ту же плотность, что и треугольник Шварца, из которого он образован, это не всегда так. Во-первых, многогранники, грани которых проходят через центр модели (включая гемиполиэдры, большой диромбикосододекаэдр, и большой дизнуб диргомбидодекаэдр ) не имеют четко определенной плотности. Во-вторых, искажение, необходимое для восстановления однородности при замене сферического многогранника на его плоский аналог, может проталкивать грани через центр многогранника и отступать с другой стороны, изменяя плотность. Это происходит в следующих случаях:
- В большой усеченный кубооктаэдр, 2 3 4/3 |. В то время как треугольник Шварца (2 3 4/3) имеет плотность 7, восстановление однородности проталкивает восемь шестиугольников через центр, давая плотность | 7 - 8 | = 1, то же, что и у колунарного треугольника Шварца (2 3 4), который разделяет те же большие круги.
- В усеченный додекадодекаэдр, 2 5/3 5 |. В то время как треугольник Шварца (2 5/3 5) имеет плотность 9, восстановление однородности проталкивает двенадцать декагонов через центр, давая плотность | 9 - 12 | = 3, то же, что и у колунарного треугольника Шварца (2 5/2 5), который разделяет те же большие круги.
- Три курносых многогранника: большой икосаэдр | 2 3/2 3/2, малый ретроснуб икосикосододекаэдр | 3/2 3/2 5/2, а большой ретроснуб икосододекаэдр | 2 3/2 5/3. Здесь вершинные фигуры были искажены в пентаграммы или гексаграммы, а не в пятиугольники или шестиугольники, проталкивая все курносые треугольники через центр и получая плотности | 5 - 12 | = 7, | 22 - 60 | = 38 и | 23 - 60 | = 37 соответственно. Эти плотности такие же, как у колонных рефлекстреугольники Шварца, не указанные выше. Таким образом, можно считать, что большой икосаэдр произошел от (2/3 3 3) или (2 3 3/4), малый ретроснуб икосикосододекаэдр - от (3 3 5/8) или (3 3/4 5/3), и большой ретроснуб икосидодекаэдр из (2/3 3 5/2), (2 3/4 5/3) или (2 3 5/7). (Кокстер, «Равномерные многогранники», 1954).
Таблица результатов


Есть семь точек генератора с каждым набором p, q, r (и несколькими специальными формами):
| Общий | Правый треугольник (r = 2) | ||||||
|---|---|---|---|---|---|---|---|
| Описание | Wythoff символ | Вершина конфигурация | Coxeter диаграмма | Wythoff символ | Вершина конфигурация | Schläfli символ | Coxeter диаграмма |
| обычный и квазирегулярный | q | п р | (p.r)q | q | п 2 | пq | {p, q} | ||
| p | q r | (q.r)п | p | q 2 | qп | {q, p} | |||
| г | p q | (q.p)р | 2 | p q | (q.p) ² | т1{p, q} | |||
| усеченный и расширенный | q r | п | q.2p.r.2p | q 2 | п | q.2p.2p | т0,1{p, q} | ||
| p r | q | p.2q.r.2q | п 2 | q | п. 2 кв. 2 кв. | т0,1{q, p} | |||
| p q | р | 2р. Кв. 2р. П. | p q | 2 | 4.q.4.p | т0,2{p, q} | |||
| ровный | p q r | | 2р. 2кв. 2п | p q 2 | | 4.2q. 2p | т0,1,2{p, q} | ||
| p q р s | | 2р. 2кв.-2п.-2кв | - | п 2 р s | | 2п.4.-2п.4/3 | - | ||
| пренебрежительно | | p q r | 3.r.3.q.3.p | | p q 2 | 3.3.q.3.p | sr {p, q} | ||
| | p q r s | (4.p.4.q.4.r.4.s) / 2 | - | - | - | - | ||
Есть четыре особых случая:
- p q р
s | - Это смесь p q r | и p q s |. Оба символа p q r | и p q s | создать общий базовый многогранник с некоторыми дополнительными гранями. Обозначение p q р
s | затем представляет собой базовый многогранник, составленный из граней, общих для обоих p q r | и p q s |. - | p q r - Курносым формам (чередующимся) присваивается этот неиспользуемый символ.
- | p q r s - Уникальная курносая форма для U75 это не может быть построено Уайтхоффом с использованием треугольных фундаментальных областей. В этот символ Wythoff включены четыре числа, поскольку этот многогранник имеет тетрагональную сферическую фундаментальную область.
- | (p) q (r) s - Уникальная курносая форма для Фигура Скиллинга это не конструктивно Уайтхофф.
Эта таблица преобразования из символа Wythoff в конфигурацию вершины не работает для пяти исключительных многогранников, перечисленных выше, чьи плотности не совпадают с плотностями их генерирующих мозаик треугольников Шварца. В этих случаях вершинная фигура сильно искажается для достижения однородности с плоскими гранями: в первых двух случаях это тупой треугольник вместо острого треугольника, а в последних трех - пентаграмма или гексаграмма вместо пятиугольника или шестиугольника, дважды оборачиваясь вокруг центра. Это приводит к тому, что некоторые грани проталкиваются прямо через многогранник по сравнению с топологически эквивалентными формами без искажения вершинной фигуры и выходят ретроградно на другой стороне.[1]
Двугранный (призматический)
В двугранных треугольниках Шварца два числа равны 2, а третье может быть любым. Рациональное число строго больше 1.
- (2 2 п/d) - вырождены, если gcd (п, d) > 1.
Многие многогранники с двугранной симметрией имеют Digon грани, которые делают их вырожденными многогранниками (например, дигедра и Hosohedra ). Столбцы таблицы, которые дают только вырожденные однородные многогранники, не включаются: специальные вырожденные случаи (только в (2 2 2) треугольнике Шварца) отмечены большим крестом. Униформа скрещенные антипризмы с основанием {п} куда п <3/2 не могут существовать, поскольку их фигуры вершин нарушит треугольное неравенство; они также отмечены большим крестом. Скрещенная на 3/2 антипризма (trirp) является вырожденной, плоской в евклидовом пространстве и также отмечена большим крестом. Треугольники Шварца (2 2 п/d) указаны здесь, только если gcd (п, d) = 1, иначе получаются только вырожденные однородные многогранники.
В списке ниже приведены все возможные случаи, когда п ≤ 6.
| (p q r) | q r | п q.2p.r.2p | p r | q п. 2кв. 2кв. | p q r | 2р. 2кв. 2п | | p q r 3.r.3.q.3.p |
|---|---|---|---|---|
| (2 2 2) (μ = 1) | 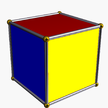 4.4.4 куб 4-п |  3.3.3 тет 2-к. | ||
| (2 2 3) (μ = 1) |  4.3.4 путешествие 3-п |  4.3.4 путешествие 3-п | 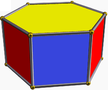 6.4.4 бедро 6-п |  3.3.3.3 окт 3-кв |
| (2 2 3/2) (μ = 2) |  4.3.4 путешествие 3-п |  4.3.4 путешествие 3-п |  6/2.4.4 2 поездка 6/2-п | |
| (2 2 4) (μ = 1) |  4.4.4 куб 4-п |  4.4.4 куб 4-п |  8.4.4 op 8-п |  3.4.3.3 сплющиваться 4-кв |
| (2 2 4/3) (μ = 3) |  4.4.4 куб 4-п |  4.4.4 куб 4-п | 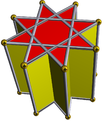 8/3.4.4 остановка 8/3-п | |
| (2 2 5) (μ = 1) |  4.5.4 пип 5-п |  4.5.4 пип 5-п |  10.4.4 окунать 10-п |  3.5.3.3 папа 5-кв |
| (2 2 5/2) (μ = 2) |  4.5/2.4 оговорка 5/2-п |  4.5/2.4 оговорка 5/2-п |  10/2.4.4 2 пункта 10/2-п |  3.5/2.3.3 скоба 5/2-кв |
| (2 2 5/3) (μ = 3) |  4.5/2.4 оговорка 5/2-п |  4.5/2.4 оговорка 5/2-п |  10/3.4.4 Стидип 10/3-п | 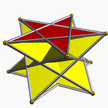 3.5/3.3.3 старп 5/3-кв |
| (2 2 5/4) (μ = 4) |  4.5.4 пип 5-п |  4.5.4 пип 5-п |  10/4.4.4 – 10/4-п | |
| (2 2 6) (μ = 1) |  4.6.4 бедро 6-п |  4.6.4 бедро 6-п |  12.4.4 твип 12-п |  3.6.3.3 случай 6-кв |
| (2 2 6/5) (μ = 5) |  4.6.4 бедро 6-п |  4.6.4 бедро 6-п |  12/5.4.4 трепать 12/5-п | |
| (2 2 п) (μ = 1) | 4.п.4 п-п | 4.п.4 п-п | 2п.4.4 2п-п | 3.п.3.3 п-ap |
| (2 2 п/d) (μ =d) | 4.п/d.4 п/d-п | 4.п/d.4 п/d-п | 2п/d.4.4 2п/d-п | 3.п/d.3.3 п/d-ap |
Тетраэдр
В четырехгранных треугольниках Шварца максимально допустимый числитель - 3.
| # | (p q r) | q | п р (p.r)q | p | q r (q.r)п | г | p q (q.p)р | q r | п q.2p.r.2p | p r | q п. 2кв. 2кв. | p q | р 2р. Кв. 2р. П. | p q r | 2р. 2кв. 2п | | p q r 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|---|
| 1 | (3 3 2) (µ = 1) |  3.3.3 тет U1 |  3.3.3 тет U1 |  3.3.3.3 окт U5 |  3.6.6 гудок U2 |  3.6.6 гудок U2 |  4.3.4.3 co U7 |  4.6.6 палец U8 |  3.3.3.3.3 Айк U22 |
| 2 | (3 3 3/2) (µ = 2) |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  3.6.3/2.6 охо U3 |  3.6.3/2.6 охо U3 |  2(6/2.3.6/2.3) 2октябрь – |  2(6/2.6.6) 2тут – |  2(3.3/2.3.3.3.3) 2октябрь + 8 {3} – |
| 3 | (3 2 3/2) (µ = 3) |  3.3.3.3 окт U5 |  3.3.3 тет U1 |  3.3.3 тет U1 |  3.6.6 гудок U2 |  2(3/2.4.3.4) 2та U4 * |  3(3.6/2.6/2) 3тет – |  2(6/2.4.6) cho + 4 {6/2} U15 * |  3(3.3.3) 3тет – |
| 4 | (2 3/2 3/2) (µ = 5) |  3.3.3 тет U1 |  3.3.3.3 окт U5 |  3.3.3 тет U1 |  3.4.3.4 co U7 |  3(6/2.3.6/2) 3тет – |  3(6/2.3.6/2) 3тет – |  4(6/2.6/2.4) 2 окт. + 6 {4} – |  (3.3.3.3.3)/2 gike U53 |
| 5 | (3/2 3/2 3/2) (µ = 6) |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  (3.3.3.3.3.3)/2 2тет – |  2(6/2.3.6/2.3) 2октябрь – |  2(6/2.3.6/2.3) 2октябрь – |  2(6/2.3.6/2.3) 2октябрь – |  6(6/2.6/2.6/2) 6тет – |
Восьмигранный
В октаэдрических треугольниках Шварца максимально допустимый числитель равен 4. Существуют также октаэдрические треугольники Шварца, в которых используется число 4/2, но они приводят только к вырожденным однородным многогранникам, поскольку 4 и 2 имеют общие фактор.
| # | (p q r) | q | п р (p.r)q | p | q r (q.r)п | г | p q (q.p)р | q r | п q.2p.r.2p | p r | q п. 2кв. 2кв. | p q | р 2р. Кв. 2р. П. | p q r | 2р. 2кв. 2п | | p q r 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|---|
| 1 | (4 3 2) (µ = 1) |  4.4.4 куб U6 |  3.3.3.3 окт U5 |  3.4.3.4 co U7 |  3.8.8 тик U9 |  4.6.6 палец U8 |  4.3.4.4 сирко U10 | 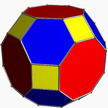 4.6.8 девушка U11 |  3.3.3.3.4 хихикать U12 |
| 2 | (4 4 3/2) (µ = 2) |  (3/2.4)4 окт + 6 {4} – |  (3/2.4)4 окт + 6 {4} – |  (4.4.4.4.4.4)/2 2куб – |  3/2.8.4.8 Socco U13 |  3/2.8.4.8 Socco U13 |  2(6/2.4.6/2.4) 2co – |  2(6/2.8.8) 2tic – | |
| 3 | (4 3 4/3) (µ = 4) |  (4.4.4.4.4.4)/2 2куб – |  (3/2.4)4 окт + 6 {4} – |  (3/2.4)4 окт + 6 {4} – |  3/2.8.4.8 Socco U13 |  2(4/3.6.4.6) 2cho U15 * |  3.8/3.4.8/3 Gocco U14 | 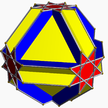 6.8.8/3 котко U16 | |
| 4 | (4 2 3/2) (µ = 5) |  3.4.3.4 co U7 |  3.3.3.3 окт U5 |  4.4.4 куб U6 |  3.8.8 тик U9 |  4.4.3/2.4 Querco U17 |  4(4.6/2.6/2) 2 окт. + 6 {4} – |  2(4.6/2.8) sroh + 8 {6/2} U18 * | |
| 5 | (3 2 4/3) (µ = 7) |  3.4.3.4 co U7 |  4.4.4 куб U6 |  3.3.3.3 окт U5 |  4.6.6 палец U8 |  4.4.3/2.4 Querco U17 |  3.8/3.8/3 Quith U19 | 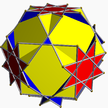 4.6/5.8/3 Quitco U20 | |
| 6 | (2 3/2 4/3) (µ = 11) |  4.4.4 куб U6 |  3.4.3.4 co U7 |  3.3.3.3 окт U5 |  4.3.4.4 сирко U10 |  4(4.6/2.6/2) 2 окт. + 6 {4} – |  3.8/3.8/3 Quith U19 |  2(4.6/2.8/3) groh + 8 {6/2} U21 * | |
| 7 | (3/2 4/3 4/3) (µ = 14) |  (3/2.4)4 = (3.4)4/3 окт + 6 {4} – |  (4.4.4.4.4.4)/2 2куб – |  (3/2.4)4 = (3.4)4/3 окт + 6 {4} – |  2(6/2.4.6/2.4) 2co – |  3.8/3.4.8/3 Gocco U14 |  3.8/3.4.8/3 Gocco U14 |  2(6/2.8/3.8/3) 2quith – |
Икосаэдр
В икосаэдрических треугольниках Шварца максимально допустимый числитель равен 5. Кроме того, числитель 4 вообще нельзя использовать в икосаэдральных треугольниках Шварца, хотя числители 2 и 3 разрешены. (Если бы 4 и 5 могли встречаться вместе в каком-то треугольнике Шварца, они должны были бы встречаться вместе и в каком-нибудь треугольнике Мёбиуса; но это невозможно, поскольку (2 4 5) - это гиперболический треугольник, а не сферический.)
| # | (p q r) | q | п р (p.r)q | p | q r (q.r)п | г | p q (q.p)р | q r | п q.2p.r.2p | p r | q п. 2кв. 2кв. | p q | р 2р. Кв. 2р. П. | p q r | 2р. 2кв. 2п | | p q r 3.r.3.q.3.p |
|---|---|---|---|---|---|---|---|---|---|
| 1 | (5 3 2) (µ = 1) |  5.5.5 лань U23 |  3.3.3.3.3 Айк U22 |  3.5.3.5 я бы U24 |  3.10.10 tid U26 |  5.6.6 ти U25 |  4.3.4.5 грязный U27 | 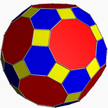 4.6.10 сетка U28 |  3.3.3.3.5 насмехаться U29 |
| 2 | (3 3 5/2) (µ = 2) |  3.5/2.3.5/2.3.5/2 сидтид U30 |  3.5/2.3.5/2.3.5/2 сидтид U30 |  (310)/2 2ike – |  3.6.5/2.6 siid U31 |  3.6.5/2.6 siid U31 |  2(10/2.3.10/2.3) 2id – |  2(10/2.6.6) 2ti – |  3.5/2.3.3.3.3 сбоку U32 |
| 3 | (5 5 3/2) (µ = 2) |  (5.3/2)5 Сид – |  (5.3/2)5 Сид – |  (5.5.5.5.5.5)/2 2doe – |  5.10.3/2.10 Саддид U33 |  5.10.3/2.10 Саддид U33 |  2(6/2.5.6/2.5) 2id – |  2(6/2.10.10) 2тид – |  2(3.3/2.3.5.3.5) 2id + 40 {3} – |
| 4 | (5 5/2 2) (µ = 3) |  (5.5.5.5.5)/2 болтать U35 |  5/2.5/2.5/2.5/2.5/2 сиссид U34 |  5/2.5.5/2.5 сделал U36 |  5/2.10.10 жесткий U37 |  5.10/2.10/2 3доу – |  4.5/2.4.5 рейдовый U38 |  2(4.10/2.10) sird + 12 {10/2} U39 * |  3.3.5/2.3.5 Сиддид U40 |
| 5 | (5 3 5/3) (µ = 4) |  5.5/3.5.5/3.5.5/3 ditdid U41 |  (3.5/3)5 тусклый – |  (3.5)5/3 Сид – |  3.10.5/3.10 Сиддитдид U43 |  5.6.5/3.6 идея U44 |  10/3.3.10/3.5 gidditdid U42 |  10/3.6.10 бездельник U45 |  3.5/3.3.3.3.5 односторонний U46 |
| 6 | (5/2 5/2 5/2) (µ = 6) |  (5/2)10/2 2sissid – |  (5/2)10/2 2sissid – |  (5/2)10/2 2sissid – |  2(5/2.10/2)2 2did – |  2(5/2.10/2)2 2did – |  2(5/2.10/2)2 2did – |  6(10/2.10/2.10/2) 6doe – |  3(3.5/2.3.5/2.3.5/2) 3 сидтид – |
| 7 | (5 3 3/2) (µ = 6) |  (3.5.3.5.3.5)/2 головокружение U47 |  (310)/4 2gike – |  (3.5.3.5.3.5)/2 головокружение U47 |  2(3.10.3/2.10) 2сейхид U49 * |  5.6.3/2.6 giid U48 |  5(6/2.3.6/2.5) 3ike + gad – |  2(6.6/2.10) Сидди + 20 {6/2} U50 * |  5(3.3.3.3.3.5)/2 5ike + gad – |
| 8 | (5 5 5/4) (µ = 6) |  (510)/4 2gad – |  (510)/4 2gad – |  (510)/4 2gad – |  2(5.10.5/4.10) 2sidhid U51 * |  2(5.10.5/4.10) 2sidhid U51 * |  10/4.5.10/4.5 2did – |  2(10/4.10.10) 2тигид – |  3(3.5.3.5.3.5) 3cid – |
| 9 | (3 5/2 2) (µ = 7) |  (3.3.3.3.3)/2 gike U53 |  5/2.5/2.5/2 гиссид U52 |  5/2.3.5/2.3 гид U54 |  5/2.6.6 тигги U55 |  3.10/2.10/2 2gad + ike – |  3(4.5/2.4.3) sicdatrid – |  4.10/2.6 ri + 12 {10/2} U56 * |  3.3.5/2.3.3 госид U57 |
| 10 | (5 5/2 3/2) (µ = 8) |  (5.3/2)5 Сид – |  (5/3.3)5 тусклый – |  5.5/3.5.5/3.5.5/3 ditdid U41 |  5/3.10.3.10 Сиддитдид U43 |  5(5.10/2.3.10/2) ike + 3gad – |  3(6/2.5/2.6/2.5) сидтид + головокружение – |  4(6/2.10/2.10) id + seihid + sidhid – | (3|3 5/2) + (3/2|3 5) |
| 11 | (5 2 5/3) (µ = 9) |  5.5/2.5.5/2 сделал U36 |  5/2.5/2.5/2.5/2.5/2 сиссид U34 |  (5.5.5.5.5)/2 болтать U35 |  5/2.10.10 жесткий U37 |  3(5.4.5/3.4) cadditradid – |  10/3.5.5 бросить сиссид U58 |  10/3.4.10/9 бросил U59 |  3.5/3.3.3.5 isdid U60 |
| 12 | (3 5/2 5/3) (µ = 10) |  (3.5/3)5 тусклый – |  (5/2)6/2 2gissid – |  (5/2.3)5/3 тусклый – |  2(5/2.6.5/3.6) 2sidhei U62 * |  3(3.10/2.5/3.10/2) ditdid + gidtid – |  10/3.5/2.10/3.3 гаддид U61 |  10/3.10/2.6 головокружение + 12 {10/2} U63 * |  3.5/3.3.5/2.3.3 гисдид U64 |
| 13 | (5 3 5/4) (µ = 10) |  (5.5.5.5.5.5)/2 2doe – |  (3/2.5)5 Сид – |  (3.5)5/3 Сид – |  3/2.10.5.10 Саддид U33 |  2(5.6.5/4.6) 2gidhei U65 * |  3(10/4.3.10/4.5) сидтид + дитдид – |  2(10/4.6.10) Сидди + 12 {10/4} U50 * | |
| 14 | (5 2 3/2) (µ = 11) |  5.3.5.3 я бы U24 |  3.3.3.3.3 Айк U22 |  5.5.5 лань U23 |  3.10.10 tid U26 |  3(5/4.4.3/2.4) gicdatrid – |  5(5.6/2.6/2) 2ike + gad – |  2(6/2.4.10) sird + 20 {6/2} U39 * |  5(3.3.3.5.3)/2 4ike + gad – |
| 15 | (3 2 5/3) (µ = 13) |  3.5/2.3.5/2 гид U54 |  5/2.5/2.5/2 гиссид U52 |  (3.3.3.3.3)/2 gike U53 |  5/2.6.6 тигги U55 |  3.4.5/3.4 qrid U67 |  10/3.10/3.3 бросить gissid U66 |  10/3.4.6 гакватид U68 |  3.5/3.3.3.3 гисид U69 |
| 16 | (5/2 5/2 3/2) (µ = 14) |  (5/3.3)5 тусклый – |  (5/3.3)5 тусклый – |  (5/2)6/2 2gissid – |  3(5/3.10/2.3.10/2) ditdid + gidtid – |  3(5/3.10/2.3.10/2) ditdid + gidtid – |  2(6/2.5/2.6/2.5/2) 2gid – |  10(6/2.10/2.10/2) 2ike + 4gad – | |
| 17 | (3 3 5/4) (µ = 14) |  (3.5.3.5.3.5)/2 головокружение U47 |  (3.5.3.5.3.5)/2 головокружение U47 |  (3)10/4 2gike – |  3/2.6.5.6 giid U48 |  3/2.6.5.6 giid U48 |  2(10/4.3.10/4.3) 2gid – |  2(10/4.6.6) 2тигги – | |
| 18 | (3 5/2 5/4) (µ = 16) |  (3/2.5)5 Сид – |  5/3.5.5/3.5.5/3.5 ditdid U41 |  (5/2.3)5/3 тусклый – |  5/3.6.5.6 идея U44 |  5(3/2.10/2.5.10/2) ike + 3gad – |  5(10/4.5/2.10/4.3) 3sissid + gike – |  4(10/4.10/2.6) did + sidhei + gidhei – | |
| 19 | (5/2 2 3/2) (µ = 17) |  3.5/2.3.5/2 гид U54 |  (3.3.3.3.3)/2 gike U53 |  5/2.5/2.5/2 гиссид U52 |  5(10/2.3.10/2) 2gad + ike – |  5/3.4.3.4 qrid U67 |  5(6/2.6/2.5/2) 2gike + sissid – |  6(6/2.4.10/2) 2gidtid + ром – | |
| 20 | (5/2 5/3 5/3) (µ = 18) |  (5/2)10/2 2sissid – |  (5/2)10/2 2sissid – |  (5/2)10/2 2sissid – |  2(5/2.10/2)2 2did – |  2(5/2.10/3.5/3.10/3) 2gidhid U70 * |  2(5/2.10/3.5/3.10/3) 2gidhid U70 * |  2(10/3.10/3.10/2) 2квициссид – | |
| 21 | (3 5/3 3/2) (µ = 18) |  (310)/2 2ike – |  5/2.3.5/2.3.5/2.3 сидтид U30 |  5/2.3.5/2.3.5/2.3 сидтид U30 |  5/2.6.3.6 siid U31 |  2(3.10/3.3/2.10/3) 2гейхид U71 * |  5(6/2.5/3.6/2.3) sissid + 3gike – |  2(6/2.10/3.6) головокружение + 20 {6/2} U63 * | |
| 22 | (3 2 5/4) (µ = 19) |  3.5.3.5 я бы U24 |  5.5.5 лань U23 |  3.3.3.3.3 Айк U22 |  5.6.6 ти U25 |  3(3/2.4.5/4.4) gicdatrid – |  5(10/4.10/4.3) 2sissid + gike – |  2(10/4.4.6) ri + 12 {10/4} U56 * | |
| 23 | (5/2 2 5/4) (µ = 21) |  5/2.5.5/2.5 сделал U36 |  (5.5.5.5.5)/2 болтать U35 |  5/2.5/2.5/2.5/2.5/2 сиссид U34 |  3(10/2.5.10/2) 3доу – |  3(5/3.4.5.4) cadditradid – |  3(10/4.5/2.10/4) 3gissid – |  6(10/4.4.10/2) 2ditdid + ром – | |
| 24 | (5/2 3/2 3/2) (µ = 22) |  5/2.3.5/2.3.5/2.3 сидтид U30 |  (310)/2 2ike – |  5/2.3.5/2.3.5/2.3 сидтид U30 |  2(3.10/2.3.10/2) 2id – |  5(5/3.6/2.3.6/2) sissid + 3gike – |  5(5/3.6/2.3.6/2) sissid + 3gike – |  10(6/2.6/2.10/2) 4ike + 2gad – |  (3.3.3.3.3.5/2)/2 господин U72 |
| 25 | (2 5/3 3/2) (µ = 23) |  (3.3.3.3.3)/2 gike U53 |  5/2.3.5/2.3 гид U54 |  5/2.5/2.5/2 гиссид U52 |  3(5/2.4.3.4) sicdatrid – |  10/3.3.10/3 бросить gissid U66 |  5(6/2.5/2.6/2) 2gike + sissid – |  2(6/2.10/3.4) пояс + 20 {6/2} U73 * |  (3.3.3.5/2.3)/2 гирсид U74 |
| 26 | (5/3 5/3 3/2) (µ = 26) |  (5/2.3)5/3 тусклый – |  (5/2.3)5/3 тусклый – |  (5/2)6/2 2gissid – |  5/2.10/3.3.10/3 гаддид U61 |  5/2.10/3.3.10/3 гаддид U61 |  2(6/2.5/2.6/2.5/2) 2gid – |  2(6/2.10/3.10/3) 2квитгиссид – | |
| 27 | (2 5/3 5/4) (µ = 27) |  (5.5.5.5.5)/2 болтать U35 |  5/2.5.5/2.5 сделал U36 |  5/2.5/2.5/2.5/2.5/2 сиссид U34 |  5/2.4.5.4 рейдовый U38 |  10/3.5.10/3 бросить сиссид U58 |  3(10/4.5/2.10/4) 3gissid – |  2(10/4.10/3.4) пояс + 12 {10/4} U73 * | |
| 28 | (2 3/2 5/4) (µ = 29) |  5.5.5 лань U23 |  3.5.3.5 я бы U24 |  3.3.3.3.3 Айк U22 |  3.4.5.4 грязный U27 |  2(6/2.5.6/2) 2ike + gad – |  5(10/4.3.10/4) 2sissid + gike – |  6(10/4.6/2.4/3) 2сидтид + ром – | |
| 29 | (5/3 3/2 5/4) (µ = 32) |  5/3.5.5/3.5.5/3.5 ditdid U41 |  (3.5)5/3 Сид – |  (3.5/2)5/3 тусклый – |  3.10/3.5.10/3 gidditdid U42 |  3(5/2.6/2.5.6/2) сидтид + головокружение – |  5(10/4.3.10/4.5/2) 3sissid + gike – |  4(10/4.6/2.10/3) гид + гейхид + гидхид – | |
| 30 | (3/2 3/2 5/4) (µ = 34) |  (3.5.3.5.3.5)/2 головокружение U47 |  (3.5.3.5.3.5)/2 головокружение U47 |  (3)10/4 2gike – |  5(3.6/2.5.6/2) 3ike + gad – |  5(3.6/2.5.6/2) 3ike + gad – |  2(10/4.3.10/4.3) 2gid – |  10(10/4.6/2.6/2) 2sissid + 4gike – | |
| 31 | (3/2 5/4 5/4) (µ = 38) |  (3.5)5/3 Сид – |  (5.5.5.5.5.5)/2 2doe – |  (3.5)5/3 Сид – |  2(5.6/2.5.6/2) 2id – |  3(3.10/4.5/4.10/4) сидтид + дитдид – |  3(3.10/4.5/4.10/4) сидтид + дитдид – |  10(10/4.10/4.6/2) 4sissid + 2gike – |  5(3.3.3.5/4.3.5/4) 4ike + 2gad – |
| 32 | (5/4 5/4 5/4) (µ = 42) |  (5)10/4 2gad – |  (5)10/4 2gad – |  (5)10/4 2gad – |  2(5.10/4.5.10/4) 2did – |  2(5.10/4.5.10/4) 2did – |  2(5.10/4.5.10/4) 2did – |  6(10/4.10/4.10/4) 2gissid – |  3(3/2.5.3/2.5.3/2.5) 3cid – |
Не вайтхоффианцы
Hemi формы
Эти многогранники ( гемиполиэдры ) порождаются как двойные покрытия конструкцией Витхоффа. Если фигура, созданная конструкцией Wythoff, состоит из двух идентичных компонентов, оператор "hemi" принимает только один. В октагемиоктаэдр включен в таблицу для полноты, хотя не создается как двойное покрытие конструкцией Wythoff.
 3/2.4.3.4 та U4 пол (3 3/2 | 2) |  4/3.6.4.6 чо U15 полу (4 4/3 | 3) |  5/4.10.5.10 Сидхид U51 полу (5 5/4 | 5) |  5/2.6.5/3.6 сидхеи U62 пол (5/2 5/3 | 3) |  5/2.10/3.5/3.10/3 гидхид U70 Hemi (5/2 5/3 | 5/3) |
 3/2.6.3.6 охо U3 Хеми (?) |  3/2.10.3.10 Сейхид U49 полу (3 3/2 | 5) |  5.6.5/4.6 гидхей U65 пол (5 5/4 | 3) |  3.10/3.3/2.10/3 Гейхид U71 пол (3 3/2 | 5/3) |
Уменьшенные формы
Эти многогранники порождаются с дополнительными гранями конструкцией Уайтхоффа. Если фигура создается конструкцией Wythoff как состоящая из двух или трех неидентичных компонентов, оператор «уменьшенный» удаляет лишние грани (которые должны быть указаны) из фигуры, оставляя только один компонент.
| Wythoff | Многогранник | Дополнительные лица | Wythoff | Многогранник | Дополнительные лица | Wythoff | Многогранник | Дополнительные лица | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 3 2 3/2 | |  4.6.4/3.6 чо U15 | 4{6/2} | 4 2 3/2 | |  4.8.4/3.8/7 сро U18 | 8{6/2} | 2 3/2 4/3 | |  4.8/3.4/3.8/5 Groh U21 | 8{6/2} | ||
| 5 5/2 2 | |  4.10.4/3.10/9 сирд U39 | 12{10/2} | 5 3 3/2 | |  10.6.10/9.6/5 Сидди U50 | 20{6/2} | 3 5/2 2 | |  6.4.6/5.4/3 ри U56 | 12{10/2} | ||
| 5 5/2 3/2 | |  3/2.10.3.10 Сейхид U49 | id + сидхид | 5 5/2 3/2 | |  5/4.10.5.10 Сидхид U51 | id + seihid | 5 3 5/4 | |  10.6.10/9.6/5 Сидди U50 | 12{10/4} | ||
| 3 5/2 5/3 | |  6.10/3.6/5.10/7 головокружение U63 | 12{10/2} | 5 2 3/2 | |  4.10/3.4/3.10/9 сирд U39 | 20{6/2} | 3 5/2 5/4 | |  5.6.5/4.6 гидхей U65 | сделал + сидхеи | ||
| 3 5/2 5/4 | |  5/2.6.5/3.6 сидхеи U62 | сделал + гидхей | 3 5/3 3/2 | |  6.10/3.6/5.10/7 головокружение U63 | 20{6/2} | 3 2 5/4 | |  6.4.6/5.4/3 ри U56 | 12{10/4} | ||
| 2 5/3 3/2 | |  4.10/3.4/3.10/7 подпоясанный U73 | 20{6/2} | 5/3 3/2 5/4 | |  3.10/3.3/2.10/3 Гейхид U71 | гид + гидхид | 5/3 3/2 5/4 | |  5/2.10/3.5/3.10/3 гидхид U70 | гид + гейхид | ||
| 2 5/3 5/4 | |  4.10/3.4/3.10/7 подпоясанный U73 | 12{10/4} |
В тетрагемигексаэдр (thah, U4) также является сокращенной версией {3/2} -купол (ретроградный треугольный купол, ратрику) автор: {6/2}. Таким образом, его также можно назвать перекрещенный треугольный куплоид.
Многие приведенные выше случаи являются производными от вырожденных всесторонне усеченные многогранники р д г |. В этих случаях два различных вырожденных случая p q r | и p q s | могут быть сгенерированы из тех же p и q; результат имеет грани {2p}, {2q} и совпадающие лица {2r} или {2s} соответственно. Они оба дают одни и те же невырожденные однородные многогранники, когда отбрасываются совпадающие грани, которые Кокстер символизировал p q р
s |, Эти случаи перечислены ниже:
 4.6.4/3.6 чо U15 2 3 3/2 3/2 | |  4.8.4/3.8/7 сро U18 2 3 3/2 4/2 | |  4.10.4/3.10/9 сирд U39 2 3 3/2 5/2 | |  6.10/3.6/5.10/7 головокружение U63 3 5/3 3/2 5/2 | |
 6.4.6/5.4/3 ри U56 2 3 5/4 5/2 | |  4.8/3.4/3.8/5 Groh U21 2 4/3 3/2 4/2 | |  4.10/3.4/3.10/7 подпоясанный U73 2 5/3 3/2 5/4 | |  10.6.10/9.6/5 Сидди U50 3 5 3/2 5/4 | |
В малых и больших ромбогексаэдрах используется дробь 4/2, несмотря на то, что она не является наименьшей. Пока 2 4 2 | и 2 4/3 2 | представляют собой одиночную восьмиугольную или восьмиугольную призму соответственно 2 4 4/2 | и 2 4/3 4/2 | представляют собой три такие призмы, которые имеют общие квадратные грани (именно те, которые сложены вдвое, чтобы получить {8/2}). Эти {8/2} имеют четырехчастную, а не двукратную симметрию вращения, оправдывая использование 4/2 вместо 2.[1]
Другие формы
Эти два однородных многогранника вообще не могут быть порождены конструкцией Уайтхоффа. Это набор однородных многогранников, обычно описываемых как «не-Wythoffians». Вместо треугольный фундаментальные области однородных многогранников Витофова, эти два многогранника имеют четырехугольный фундаментальные области.
Фигура Скиллинга не указана в списке Мэдера, поскольку она экзотика однородный многогранник, с гребни (края в трехмерном случае) полностью совпадают. Это также верно для некоторых вырожденных многогранников, включенных в приведенный выше список, таких как малый сложный икосододекаэдр. Такая интерпретация совпадения ребер позволяет этим фигурам иметь две грани на ребро: если не удвоить ребра, то получится 4, 6, 8, 10 или 12 граней, встречающихся на ребре, фигуры, которые обычно исключаются как однородные многогранники. Фигура Скиллинга имеет 4 грани, пересекающиеся по краям.
| (p q r s) | | p q r s (4.p. 4.q.4.r.4.s) / 2 | | (p) q (r) s (п3.4.q.4.r3.4.s.4) / 2 |
|---|---|---|
| (3/2 5/3 3 5/2) |  (4.3/2.4.5/3.4.3.4.5/2)/2 гидрид U75 | 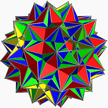 (3/23.4.5/3.4.33.4.5/2.4)/2 гидисдрид Навыки |
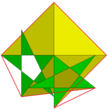 Вершинная фигура | 3 5/3 5/2 |  Большой курносый додецикосододекаэдр |  Большой диромбикосододекаэдр |  Вершинная фигура | 3/2 5/3 3 5/2 |
 Большой дизнуб диргомбидодекаэдр |  Соединение двадцати октаэдров |  Соединение двадцати тетрагемигексаэдров |  Вершинная фигура |(3/2) 5/3 (3) 5/2 |
Оба этих специальных многогранника могут быть получены из большой курносый додецикосододекаэдр, | 3 5/3 5/2 (U64). Это киральный курносый многогранник, но его пентаграммы образуют компланарные пары. При объединении одного экземпляра этого многогранника с его энантиоморфом пентаграммы совпадают и могут быть удалены. Поскольку ребра вершинной фигуры этого многогранника включают три стороны квадрата, а четвертая сторона вносится его энантиоморфом, мы видим, что полученный многогранник на самом деле является соединение двадцати октаэдров. Каждый из этих октаэдров содержит одну пару параллельных граней, которые образуются из полностью симметричного треугольника | 3 5/3 5/2, а остальные три взяты из оригинала | Курносые треугольники 3 5/3 5/2. Кроме того, каждый октаэдр можно заменить на тетрагемигексаэдр с такими же ребрами и вершинами. Взяв полностью симметричные треугольники в октаэдрах, исходные совпадающие пентаграммы в больших курносых додецикосододекаэдрах и экваториальные квадраты тетрагемигексаэдров вместе, мы получим большой диромбикосидодекаэдр (чудовище Миллера).[1] Взяв вместо этого курносые треугольники октаэдров, мы получим большой неоднозначный диргомбидодекаэдр (фигура Скиллинга).[2]
Рекомендации
- Кокстер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. С. П. (1954). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки.. Королевское общество. 246 (916): 401–450. Дои:10.1098 / рста.1954.0003. ISSN 0080-4614. JSTOR 91532. МИСТЕР 0062446.CS1 maint: ref = harv (связь) [1]
- Скиллинг, Дж. (1974). «Комплект однородных многогранников». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки.. Королевское общество. 278 (1278): 111–135. Дои:10.1098 / рста.1975.0022. ISSN 1364-503X.CS1 maint: ref = harv (связь) [2]
внешняя ссылка
Ричард Клитцинг: Многогранники
- точечно-групповая симметрия
- сложность
- Треугольники Шварца часть 1, часть 2
Цви Хар'Эль:
