Константа диссоциации кислоты - Acid dissociation constant
An константа диссоциации кислоты, Kа, (также известный как константа кислотности, или же константа кислотной ионизации) это количественный мера сила из кислота в решение. Это константа равновесия для химической реакции
известный как диссоциация в контексте кислотно-основные реакции. Химический вид HA представляет собой кислота который распадается на A−, то сопряженное основание кислоты и ион водорода, H+.[примечание 1] Говорят, что система находится в равновесие когда концентрации его компонентов не будут меняться со временем, потому что и прямые, и обратные реакции протекают с одинаковой скоростью.[1]
Константа диссоциации определяется как[заметка 2]
- , или же
где величины в квадратных скобках представляют концентрации веществ в состоянии равновесия.[заметка 3][2]
Теоретические основы
Константа диссоциации кислоты является прямым следствием лежащей в основе термодинамика реакции диссоциации; пKа значение прямо пропорционально стандарту Свободная энергия Гиббса изменение для реакции. Значение pKа изменяется с температурой и может быть понята качественно на основе Принцип Ле Шателье: когда реакция эндотермический, Kа увеличивается и pKа уменьшается с повышением температуры; обратное верно для экзотермический реакции.
Значение pKа также во многом зависит от молекулярной структуры кислоты. Например, Полинг предложил два правила: одно для последовательных pKа полипротонных кислот (см. Полипротонные кислоты ниже) и один для оценки pKа оксикислот в зависимости от числа = O и -OH групп (см. Факторы, влияющие на pKа значения ниже). Другие структурные факторы, влияющие на величину константы диссоциации кислоты, включают: индуктивные эффекты, мезомерные эффекты, и водородная связь. Уравнения типа Хэмметта часто применялись для оценки pKа.[3][4]
Количественное поведение кислот и оснований в растворе можно понять, только если их pKа значения известны. В частности, pH раствора можно предсказать, когда аналитическая концентрация и pKа значения всех кислот и оснований известны; и наоборот, можно рассчитать равновесную концентрацию кислот и оснований в растворе, если известен pH. Эти расчеты находят применение во многих областях химии, биологии, медицины и геологии. Например, многие соединения, используемые для лечения, являются слабыми кислотами или основаниями, и знание pKа ценностей вместе с коэффициент распределения октанол-вода, можно использовать для оценки степени, в которой соединение попадает в кровоток. Константы кислотной диссоциации также важны в водная химия и химическая океанография, где кислотность воды играет основную роль. В живых организмах кислотно-щелочной гомеостаз и кинетика ферментов зависят от pKа значения многих кислот и оснований, присутствующих в клетке и в организме. В химии знание pKа ценностей необходимо для подготовки буферные растворы а также является предпосылкой для количественного понимания взаимодействия между кислотами или основаниями и ионами металлов с образованием комплексы. Экспериментально pKа значения могут быть определены потенциометрическим (pH) титрование, но для значений pKа менее примерно 2 или более примерно 11, спектрофотометрический или же ЯМР измерения могут потребоваться из-за практических трудностей с измерением pH.
Определения
В соответствии с Аррениус согласно первоначальному определению, кислота - это вещество, которое диссоциирует в водном растворе, выделяя ион водорода H+ (протон):[5]
- HA ⇌ A− + H+.
Константа равновесия для этой реакции диссоциации известна как константа диссоциации. Освободившийся протон соединяется с молекулой воды, давая ион гидрокония (или оксония) ЧАС3О+ (голые протоны не существуют в растворе), и поэтому Аррениус позже предложил записать диссоциацию в виде кислотно-основная реакция:
- HA + H2O ⇌ A− + H3О+.
Бронстед и Лоури обобщил это далее на реакцию протонного обмена:[6][7][8]
- кислота + основание ⇌ сопряженное основание + сопряженная кислота.
Кислота теряет протон, оставляя сопряженное основание; протон переносится на основание, образуя сопряженную кислоту. Для водных растворов кислоты ГК основанием является вода; сопряженная база - это A− и сопряженная кислота представляет собой ион гидроксония. Определение Бренстеда – Лоури применяется к другим растворителям, таким как диметилсульфоксид: растворитель S действует как основание, принимая протон и образуя сопряженную кислоту SH+.
- HA + S ⇌ A− + SH+.
В химии растворов обычно используют H+ как сокращение для сольватированного иона водорода, независимо от растворителя. В водном растворе H+ обозначает сольватированный ион гидроксония а не протон.[9][10]
Обозначение кислоты или основания как «конъюгата» зависит от контекста. Конъюгированная кислота BH+ основания B диссоциирует согласно
- BH+ + ОН− ⇌ B + H2О
что противоположно равновесию
- ЧАС2O (кислота) + B (основание) ⇌ OH− (сопряженное основание) + BH+ (конъюгированная кислота).
В гидроксид-ион ОЙ−, хорошо известное основание, здесь действует как основание, сопряженное с кислотной водой. Таким образом, кислоты и основания рассматриваются просто как доноры и акцепторы протонов соответственно.
Более широкое определение кислотной диссоциации включает: гидролиз, в котором протоны образуются в результате расщепления молекул воды. Например, борная кислота (В (ОН)3) производит H3О+ как если бы это был донор протонов,[11] но это было подтверждено Рамановская спектроскопия что это связано с равновесием гидролиза:[12]
- В (ОН)3 + 2 часа2О ⇌ В (ОН)4− + H3О+.
По аналогии, гидролиз ионов металлов вызывает ионы, такие как [Al (H2O)6]3+ вести себя как слабые кислоты:[13]
- [Al (H2O)6]3+ + H2O ⇌ [Al (H2O)5(ОЙ)]2+ + H3О+.
В соответствии с Льюис согласно первоначальному определению, кислота - это вещество, которое принимает электронная пара сформировать координировать ковалентную связь.[14]
Константа равновесия
Константа диссоциации кислоты является частным примером константа равновесия. Диссоциация монопротовая кислота, HA, в разбавленном растворе можно записать как
- HA ⇌ A− + H+
Константа термодинамического равновесия, можно определить как[15]
где {X} представляет Мероприятия в состоянии равновесия химического вещества X. является безразмерный так как активность безразмерна. Активности продуктов диссоциации помещены в числитель, активности реагентов - в знаменатель. Видеть коэффициент активности для вывода этого выражения.

Поскольку деятельность является продуктом концентрация и коэффициент активности (γ) определение также можно было бы записать как
где [HA] представляет собой концентрацию HA и является частным от коэффициентов активности.
Чтобы избежать сложностей, связанных с использованием действий, константы диссоциации определенный, где возможно, в средней или высокой ионная сила, то есть в условиях, когда можно считать всегда постоянным.[15] Например, среда может быть раствором 0,1коренной зуб (М) нитрат натрия или 3 млн перхлорат калия. При таком предположении
получается. Обратите внимание, однако, что все опубликованные значения константы диссоциации относятся к конкретной ионной среде, использованной при их определении, и что разные значения получены при разных условиях, как показано для уксусная кислота на иллюстрации выше. Когда опубликованные константы относятся к ионной силе, отличной от той, которая требуется для конкретного приложения, они могут быть скорректированы с помощью теория конкретных ионов (СИТ) и другие теории.[16]
Накопительные и ступенчатые константы
Кумулятивная константа равновесия, обозначаемая , связана с произведением ступенчатых констант, обозначаемых . Для двухосновной кислоты соотношение между ступенчатыми и общими константами выглядит следующим образом
Обратите внимание, что в контексте образования комплексов металл-лиганд константы равновесия для образования комплексов металлов обычно определяются как ассоциация константы. В этом случае константы равновесия для протонирования лиганда также определяются как константы ассоциации. Нумерация констант ассоциации обратна нумерации констант диссоциации; в этом примере
Константы ассоциации и диссоциации
При обсуждении свойств кислот обычно определяют константы равновесия как константы диссоциации кислоты, обозначаемые как Kа, с числовыми значениями, обозначенными символом pKа.
С другой стороны, константы ассоциации используются для баз.
Тем не мение, компьютерные программы общего назначения которые используются для получения значений константы равновесия из экспериментальных данных, используют константы ассоциации как для кислот, так и для оснований. Поскольку константы стабильности для комплекса металл-лиганд всегда указываются как константы ассоциации, протонирование лиганда также должно быть указано как реакция ассоциации.[15] Определения показывают, что значение константы диссоциации кислоты обратно пропорционально значению соответствующей константы ассоциации.
- Kразобщать = 1 / Kассоциированный
- бревно Kразобщать = −log Kассоциированный
- пKразобщать = журнал Kассоциированный
Примечания
- Для данной кислоты или основания pKа + pKб = pKш, то константа самоионизации воды.
- Константа ассоциации для образования супрамолекулярный комплекс можно обозначить как Kа; в таких случаях «а» означает «ассоциация», а не «кислота».
Для полипротонных кислот нумерация констант ступенчатой ассоциации обратна нумерации констант диссоциации. Например, для фосфорная кислота (подробности в # полипротонные кислоты, ниже)
Температурная зависимость
Все константы равновесия меняются в зависимости от температура согласно уравнение Ван 'т Гоффа[17]
р это газовая постоянная и Т это абсолютная температура . Таким образом, для экзотермический реакции, стандарт изменение энтальпии, , отрицательно и K уменьшается с температурой. эндотермический реакции положительный и K увеличивается с температурой.
Стандартное изменение энтальпии реакции само по себе является функцией температуры, согласно Закон термохимии Кирхгофа:
где ΔCп это теплоемкость изменение при постоянном давлении. На практике можно считать постоянным в небольшом диапазоне температур.
Размерность
В уравнении
Kа кажется, есть размеры концентрации. Однако, поскольку , константа равновесия, , не можешь имеют физическое измерение. Этот очевидный парадокс можно разрешить разными способами.
- Предположим, что коэффициент коэффициентов активности имеет числовое значение 1, так что имеет то же числовое значение, что и константа термодинамического равновесия .
- Выразите каждое значение концентрации как отношение c / c0, где c0 это концентрация в [гипотетическом] стандартном состоянии с числовым значением 1 по определению.[18]
- Выразите концентрации на мольная доля шкала. Поскольку мольная доля не имеет размерности, отношение концентраций по определению будет чистым числом.
Процедуры (1) и (2) дают идентичные числовые значения для константы равновесия. Кроме того, поскольку концентрация, , просто пропорциональна мольной доле, и плотность,
а поскольку молярная масса является константой в разбавленных растворах, значение константы равновесия, определенное с помощью (3), будет просто пропорционально значениям, полученным с помощью (1) и (2).
Это обычная практика в биохимия чтобы указать значение с размером, например, "Kа = 30 мМ ", чтобы указать масштаб, миллимолярный (мМ) или микромолярный (мкМ) концентрация значения, используемые для его расчета.
Сильные кислоты и основания
Кислота классифицируется как «сильная», если концентрация ее недиссоциированных частиц слишком мала для измерения.[6] Любая водная кислота с п.Kа значение меньше 0 почти полностью депротонировано и считается сильная кислота.[19] Все такие кислоты переносят свои протоны в воду и образуют разновидности катионов растворителя (H3О+ в водном растворе), так что все они имеют одинаковую кислотность, явление, известное как выравнивание растворителя.[20][21] Говорят, что они полностью диссоциированный в водном растворе, потому что количество недиссоциированной кислоты, в равновесии с продуктами диссоциации, ниже Предел обнаружения.Также любая водная основа с константа ассоциации пKб менее примерно 0, что соответствует pKа больше, чем примерно 14, выравнивается до OH− и считается сильная база.[21]
Азотная кислота, с пK значение ок. -1,7, ведет себя как сильная кислота в водных растворах с pH больше 1.[22] При более низких значениях pH ведет себя как слабая кислота.
пKа значения для сильных кислот были оценены теоретически.[23] Например, pKа стоимость водных HCl был оценен как -9,3.
Монопротоновые кислоты
После перестановки выражения, определяющего Kа, и положив pH = −log10[ЧАС+], получается[24]
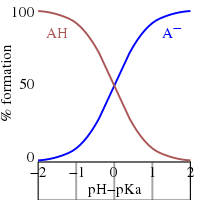
Это Уравнение Хендерсона – Хассельбаха, из чего можно сделать следующие выводы.
- При половинной нейтрализации соотношение [А−]/[HA] = 1; поскольку журнал (1) = 0, pH при полунейтрализации численно равен pKа. И наоборот, когда pH = pKа, концентрация HA равна концентрации A−.
- В буферная область простирается на примерный диапазон pKа ± 2. Слабая буферизация вне диапазона pKа ± 1. При pH ≤ pKа - 2 вещество считается полностью протонированным и при pH ≥ pKа + 2 полностью диссоциирован (депротонирован).
- Если значение pH известно, соотношение можно рассчитать. Это соотношение не зависит от аналитической концентрации кислоты.
В воде измеримое pKа значения варьируются от примерно -2 для сильной кислоты до примерно 12 для очень слабой кислоты (или сильного основания).
А буферный раствор с желаемым pH может быть приготовлена как смесь слабой кислоты и ее конъюгированного основания. На практике смесь может быть получена путем растворения кислоты в воде и добавления необходимого количества сильной кислоты или основания. Когда рKа и аналитическая концентрация кислоты известны, степень диссоциации и pH раствора монопротоновой кислоты могут быть легко рассчитаны с использованием Стол ICE.
Полипротонные кислоты

Полипротонная кислота - это соединение, которое может потерять более 1 протона. Каждая константа ступенчатой диссоциации определяется для потери одного протона. Константу диссоциации первого протона можно обозначить как Kа1 и константы диссоциации последовательных протонов как Kа2, так далее. Фосфорная кислота, H3PO4, является примером полипротонной кислоты, поскольку она может терять три протона.
Равновесие пK определение и значение[25] ЧАС
3PO
4 ⇌ ЧАС
2PO−
4 + H+ЧАС
2PO−
4 ⇌ HPO2−
4 + H+HPO2−
4 ⇌ PO3−
4 + H+
Когда разница между последовательными pK значений составляет около четырех или более, поскольку в этом примере каждый вид может рассматриваться как отдельная кислота;[26] Фактически соли ЧАС
2PO−
4 может кристаллизоваться из раствора путем доведения pH до примерно 5,5 и солей HPO2−
4 может кристаллизоваться из раствора путем доведения pH до примерно 10. Диаграмма распределения частиц показывает, что концентрации двух ионов максимальны при pH 5,5 и 10.
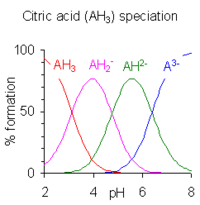
Когда разница между последовательными pK Значения меньше, чем примерно четыре, наблюдается перекрытие между диапазоном pH существования видов в равновесии. Чем меньше разница, тем больше перекрытие. Пример лимонной кислоты показан справа; растворы лимонной кислоты забуферены во всем диапазоне pH от 2,5 до 7,5.
Согласно первому правилу Полинга, последовательные pK значения данного увеличения кислоты (pKа2 > pKа1).[27] Для оксикислот с более чем одним ионизируемым водородом на одном атоме pKа значения часто увеличиваются примерно на 5 единиц за каждый удаленный протон,[28][29] как в примере с фосфорной кислотой выше.
Из таблицы выше видно, что второй протон удален от отрицательно заряженной частицы. Поскольку протон несет положительный заряд, для его удаления требуется дополнительная работа. Вот почему pKа2 больше pKа1. пKа3 больше pKа2 потому что есть дальнейшее разделение заряда. Когда обнаруживается исключение из правила Полинга, это указывает на то, что в структуре также происходят серьезные изменения. В случае VO2+ (водн.) ванадий восьмигранный, 6-координата, тогда как ванадиевая кислота четырехгранный, 4-х координатная. Это означает, что четыре «частицы» высвобождаются при первой диссоциации, но только две «частицы» высвобождаются при других диссоциациях, что приводит к гораздо большему вкладу энтропии в стандартную Свободная энергия Гиббса изменение для первой реакции, чем для других.
Равновесие пKа [VO2(ЧАС2O)4]+ ⇌ H3VO4 + H+ + 2H2О ЧАС3VO4 ⇌ ЧАС
2VO−
4 + H+ЧАС
2VO−
4 ⇌ HVO2−
4 + H+HVO2−
4 ⇌ VO3−
4 + H+
Изоэлектрическая точка
Для веществ в растворе изоэлектрическая точка (pя) определяется как pH, при котором сумма, взвешенная по величине заряда, концентраций положительно заряженных частиц равна взвешенной сумме концентраций отрицательно заряженных частиц. В случае, если существует один вид каждого типа, изоэлектрическая точка может быть получена непосредственно из pK значения. Возьмем пример глицин, определяемый как AH. Следует рассмотреть два равновесия диссоциации.
- AH+
2 ⇌ AH + H+; [АХ+] = K1[AH+
2] - AH ⇌ A− + H+; [А−][ЧАС+] = K2[AH]
Подставьте выражение для [AH] из второго уравнения в первое уравнение.
- [А−][ЧАС+]2 = K1K2[AH+
2]
В изоэлектрической точке концентрация положительно заряженных частиц AH2+, равна концентрации отрицательно заряженных частиц A−, так
- [ЧАС+]2 = K1K2
Следовательно, принимая одеколоны, pH определяется как
пя значения для аминокислот указаны в протеиногенная аминокислота. Когда более двух заряженных видов находятся в равновесии друг с другом, может потребоваться полный расчет видообразования.
Основы и основность
Константа равновесия Kб для базы обычно определяется как ассоциация константа протонирования основания B с образованием сопряженной кислоты HB+.
- B + H2O ⇌ HB+ + ОН−
Используя рассуждения, аналогичные использованным ранее
Kб относится к Kа для конъюгированной кислоты. В воде концентрация гидроксид ион, [OH−], связана с концентрацией иона водорода соотношением Kш = [H+][ОЙ−], следовательно
Замена выражения на [OH−] в выражение для Kб дает
Когда Kа, Kб и Kш определяются при одинаковых условиях температуры и ионной силы, следует, принимая одеколоны, что pKб = pKш - пKа. В водных растворах при 25 ° C, pKш составляет 13,9965,[30] так
с достаточным точность для большинства практических целей. По сути, нет необходимости определять pKб отдельно от пKа,[31] но здесь это делается как часто только pKб значения можно найти в более старой литературе.
Для гидролизованного иона металла Kб можно также определить как пошаговый диссоциация постоянный
- (ионные заряды опускаются в общих выражениях)
Это аналог константа ассоциации для формирования комплекса.
Поскольку отношение pKб = pKш - пKа имеет место только в водных растворах (хотя аналогичные соотношения применимы и для других растворителей), такие разделы химии, как органическая химия которые обычно имеют дело с неводными растворами, обычно не используют pKб как мера основности. Вместо этого pKа сопряженной кислоты, обозначаемой pKах, указывается, когда необходимо количественно определить основность. Более высокое значение pKах соответствует более сильному основанию. Например, значения pKах(C5ЧАС5N) = 5,25 и pKах((CH3CH2)3N) = 10,75 означает, что триэтиламин является более сильным основанием, чем пиридин.
Амфотерные вещества
An амфотерный Вещество - это вещество, которое может действовать как кислота или как основание, в зависимости от pH. Вода (внизу) амфотерная. Другой пример амфотерной молекулы - это бикарбонат ион HCO−
3 это сопряженное основание угольная кислота молекула H2CO3 в равновесии
- ЧАС2CO3 + H2O ⇌ HCO−
3 + H3О+
но также конъюгированная кислота карбонат ион CO2−
3 в (обратном) равновесии
- HCO−
3 + ОН− ⇌ CO2−
3 + H2О.
Угольная кислота равновесия важны для кислотно-щелочной гомеостаз в теле человека.
An аминокислота также амфотерна с дополнительным усложнением, заключающимся в том, что нейтральная молекула подчиняется внутреннему кислотно-основному равновесию, в котором основная аминогруппа притягивает и связывает протон из кислой карбоксильной группы, образуя цвиттерион.
- NH2CHRCO2H ⇌ NH+
3CHRCO−
2
При pH менее примерно 5 протонируются как карбоксилатная группа, так и аминогруппа. По мере увеличения pH кислота диссоциирует согласно
- NH+
3CHRCO
2ЧАС ⇌ NH+
3CHRCO−
2 + H+
При высоком pH может иметь место вторая диссоциация.
- NH+
3CHRCO−
2 ⇌ NH
2CHRCO−
2 + H+
Таким образом, молекула аминокислоты является амфотерной, потому что она может быть протонированной или депротонированной.
Самоионизация воды
Молекула воды может получить или потерять протон. Говорят, что это амфипротический. Ионизационное равновесие можно записать
- ЧАС2O ⇌ OH− + H+
где в водном растворе H+ обозначает растворенный протон. Часто это записывается как гидроксоний ион H3О+, но эта формула не точна, потому что на самом деле существует сольватация более чем одной молекулой воды и такими видами, как H5О2+, H7О3+ и H9О4+ также присутствуют.[32]
Константа равновесия определяется выражением
В растворах, в которых концентрация растворенных веществ не очень высока, концентрация [H2O] можно считать постоянным, независимо от растворенного вещества (веществ); это выражение можно затем заменить на
В самоионизация постоянная воды, Kш, таким образом, является просто частным случаем константы диссоциации кислоты. Логарифмическая форма, аналогичная pKа также можно определить
| Т (° C) | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| пKш | 14.943 | 14.734 | 14.535 | 14.346 | 14.167 | 13.997 | 13.830 | 13.680 | 13.535 | 13.396 | 13.262 |
Эти данные могут быть подогнаны к параболе с
- пKш = 14.94 − 0.04209Т + 0.0001718Т2
Из этого уравнения pKш = 14 при 24,87 ° С. При этой температуре ионы водорода и гидроксид-ионы имеют концентрацию 10−7 М.
Кислотность в неводных растворах
Растворитель с большей вероятностью будет способствовать ионизации растворенной молекулы кислоты в следующих случаях:[34]
- Это протонный растворитель, способные к образованию водородных связей.
- Имеет высокий номер донора, делая его сильным База Льюиса.
- Имеет высокий диэлектрическая постоянная (относительная диэлектрическая проницаемость), что делает его хорошим растворителем для ионных частиц.
пKа значения органических соединений часто получают с использованием апротонных растворителей. диметилсульфоксид (ДМСО)[34] и ацетонитрил (ACN).[35]
| Растворитель | Номер донора[34] | Диэлектрическая постоянная[34] |
|---|---|---|
| Ацетонитрил | 14 | 37 |
| Диметилсульфоксид | 30 | 47 |
| Вода | 18 | 78 |
ДМСО широко используется в качестве альтернативы воде, поскольку он имеет более низкую диэлектрическую проницаемость, чем вода, и менее полярен и поэтому растворяет неполярные, гидрофобный вещества легче. Имеет измеримое pKа диапазон примерно от 1 до 30. Ацетонитрил менее щелочной, чем ДМСО, и поэтому, как правило, кислоты слабее, а основания сильнее в этом растворителе. Некоторые пKа значения при 25 ° C для ацетонитрила (ACN)[36][37][38] и диметилсульфоксид (ДМСО).[39] показаны в следующих таблицах. Значения для воды включены для сравнения.
| HA ⇌ A− + H+ | ACN | ДМСО | Вода |
|---|---|---|---|
| п-Толуолсульфоновая кислота | 8.5 | 0.9 | Сильный |
| 2,4-динитрофенол | 16.66 | 5.1 | 3.9 |
| Бензойная кислота | 21.51 | 11.1 | 4.2 |
| Уксусная кислота | 23.51 | 12.6 | 4.756 |
| Фенол | 29.14 | 18.0 | 9.99 |
| BH+ ⇌ B + H+ | ACN | ДМСО | Вода |
| Пирролидин | 19.56 | 10.8 | 11.4 |
| Триэтиламин | 18.82 | 9.0 | 10.72 |
| Протонная губка | 18.62 | 7.5 | 12.1 |
| Пиридин | 12.53 | 3.4 | 5.2 |
| Анилин | 10.62 | 3.6 | 4.6 |
Ионизация кислот меньше в кислотном растворителе, чем в воде. Например, хлористый водород слабая кислота при растворении в уксусная кислота. Это связано с тем, что уксусная кислота - гораздо более слабое основание, чем вода.
- HCl + CH3CO2H ⇌ Cl− + CH
3С (ОН)+
2 - кислота + основание ⇌ сопряженное основание + сопряженная кислота
Сравните эту реакцию с тем, что происходит, когда уксусная кислота растворяется в более кислотном растворителе - чистой серной кислоте.[40]
ЧАС2ТАК4 + CH3CO2H ⇌ HSO−
4 + CH
3С (ОН)+
2

Маловероятный геминальный диол разновидность CH
3С (ОН)+
2 стабильна в этих средах. Для водных растворов pH шкала самая удобная функция кислотности.[41] Для неводных сред были предложены другие функции кислотности, наиболее заметной из которых является Функция кислотности Гаммета, ЧАС0, за суперкислотный СМИ и его модифицированная версия ЧАС− за сверхосновный средства массовой информации.[42]
В апротонных растворителях олигомеры, например, хорошо известная уксусная кислота димер, может быть образован водородной связью. Кислота может также образовывать водородные связи со своим сопряженным основанием. Этот процесс, известный как гомоконъюгация, обладает эффектом повышения кислотности кислот, снижая их эффективное pKа значения, стабилизируя сопряженное основание. Гомоконъюгация увеличивает протонодонорную способность толуолсульфоновой кислоты в растворе ацетонитрила почти в 800 раз.[43]
В водных растворах гомоконъюгирования не происходит, поскольку вода образует более сильные водородные связи с основанием конъюгата, чем кислота.
Смешанные растворители
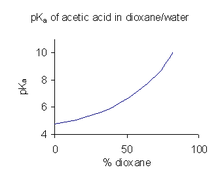
Когда соединение имеет ограниченную растворимость в воде, обычной практикой (например, в фармацевтической промышленности) является определение pKа значения в смеси растворителей, такой как вода /диоксан или вода /метанол, в котором соединение более растворимо.[45] В примере, показанном справа, pKа значение резко возрастает с увеличением процентного содержания диоксана, так как диэлектрическая проницаемость смеси уменьшается.
А пKа значение, полученное в смешанном растворителе, нельзя использовать непосредственно для водных растворов. Причина этого в том, что когда растворитель находится в стандартном состоянии, его активность определенный как один. Например, стандартное состояние смеси вода: диоксан 9: 1 соотношение смешивания это именно та смесь растворителей, без добавления растворенных веществ. Чтобы получить pKа Значение для использования с водными растворами должно быть экстраполировано до нулевой концентрации сорастворителя из значений, полученных для различных смесей сорастворителей.
Эти факты затушевываются отсутствием растворителя в выражении, которое обычно используется для определения pKа, но pKа значения, полученные в данный смешанные растворители можно сравнить друг с другом, давая относительную концентрацию кислоты. То же самое и с pKа значения, полученные в конкретном неводном растворителе, таком как ДМСО.
Универсальная, не зависящая от растворителя шкала для констант диссоциации кислоты не разработана, так как не существует известного способа сравнения стандартных состояний двух различных растворителей.
Факторы, влияющие на pKа значения
Второе правило Полинга состоит в том, что значение первого pKа для кислот формулы XOм(ОЙ)п зависит в первую очередь от количества оксогрупп м, и примерно не зависит от количества гидроксильных групп п, а также центрального атома X. Приближенные значения pKа 8 для м = 0, 2 для м = 1, −3 для м = 2 и <−10 для м = 3.[27] В качестве альтернативы были предложены различные числовые формулы, включая pKа = 8 − 5м (известный как Белла правило),[28][46] пKа = 7 − 5м,[29][47] или pKа = 9 − 7м.[28] Зависимость от м коррелирует со степенью окисления центрального атома X: чем выше степень окисления, тем сильнее оксикислота. Например, pKа для HClO - 7,2, для HClO2 составляет 2,0, для HClO3 равно -1 и HClO4 сильная кислота (пKа ≪ 0).[7] Повышенная кислотность при добавлении оксогруппы связана со стабилизацией конъюгированного основания путем делокализации его отрицательного заряда по дополнительному атому кислорода.[46] Это правило может помочь определить молекулярную структуру: например фосфористая кислота (ЧАС3PO3) имеет pKа около 2 предполагают, что структура представляет собой HPO (OH)2, как позже подтвердил ЯМР-спектроскопия, а не P (OH)3 который, как ожидается, будет иметь pKа около 8.[47]


С органическими кислотами индуктивные эффекты и мезомерные эффекты повлиять на рKа значения. Простой пример - это эффект замены атомов водорода в уксусной кислоте на более электроотрицательный атом хлора. Электроноакцепторный эффект заместителя облегчает ионизацию, поэтому последовательные pKа значения уменьшаются в ряду 4,7, 2,8, 1,4 и 0,7 при наличии 0, 1, 2 или 3 атомов хлора.[48] В Уравнение Гаммета, дает общее выражение для эффекта заместителей.[49]
- бревно(Kа) = журнал (K0
а) + ρσ.
Kа - константа диссоциации замещенного соединения, K0
а - константа диссоциации, когда заместителем является водород, ρ - свойство незамещенного соединения, а σ имеет конкретное значение для каждого заместителя. Участок из бревна (Kа) против σ - прямая с перехватить бревно(K0
а) и склон р. Это пример линейная зависимость свободной энергии как журнал (Kа) пропорционально стандартному изменению свободной энергии. Хэммет первоначально[50] сформулировал взаимосвязь с данными из бензойная кислота с разными заместителями в орто - и параграф - позиции: некоторые числовые значения указаны в Уравнение Гаммета. Это и другие исследования позволили упорядочить заместители в соответствии с их электроноакцепторный или же электроновыпускающий мощность, а также различать индукционные и мезомерные эффекты.[51][52]
Спирты обычно не ведут себя как кислоты в воде, но наличие двойной связи, смежной с группой ОН, может существенно снизить pKа по механизму кето-енольная таутомерия. Аскорбиновая кислота является примером этого эффекта. Дикетон 2,4-пентандион (ацетилацетон ) также является слабой кислотой из-за кето-енольного равновесия. В ароматических соединениях, таких как фенол, которые имеют заместитель ОН, спряжение с ароматическим кольцом в целом значительно увеличивает стабильность депротонированной формы.
Структурные эффекты также могут иметь значение. Разница между фумаровая кислота и малеиновая кислота это классический пример. Фумаровая кислота - (E) -1,4-бут-2-ендиовая кислота, a транс изомер, тогда как малеиновая кислота является соответствующей СНГ изомер, то есть (Z) -1,4-бут-2-ендиовая кислота (см. цис-транс-изомерия ). Фумаровая кислота имеет pKа значения примерно 3,0 и 4,5. Напротив, малеиновая кислота имеет pKа значения примерно 1,5 и 6,5. Причина такой большой разницы в том, что когда один протон удаляется из СНГ изомер (малеиновая кислота) сильный внутримолекулярный водородная связь образуется с соседней оставшейся карбоксильной группой. Это способствует образованию малеата H+, и он выступает против удаления второго протона из этого вида. в транс изомера, две карбоксильные группы всегда далеко друг от друга, поэтому водородная связь не наблюдается.[53]
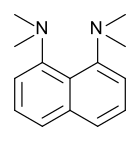
Протонная губка, 1,8-бис (диметиламино) нафталин, имеет pKа значение 12,1. Это одно из самых сильных известных аминовых оснований. Высокая основность объясняется снятием напряжения при протонировании и сильной внутренней водородной связью.[54][55]
В этом разделе также следует упомянуть о влиянии растворителя и сольватации. Оказывается, эти влияния более тонкие, чем влияние упомянутой выше диэлектрической среды. Например, ожидаемый (электронными эффектами метильных заместителей) и наблюдаемый в газовой фазе порядок основности метиламинов Me3N> Я2NH> MeNH2 > NH3, вода заменена на Меня2NH> MeNH2 > Я3N> NH3. Нейтральные молекулы метиламина связаны с молекулами воды водородными связями в основном через один акцептор, N – HOH, взаимодействие и лишь иногда еще через одну донорную связь, NH – OH.2. Следовательно, метиламины стабилизируются примерно в одинаковой степени за счет гидратации, независимо от количества метильных групп. Напротив, соответствующие катионы метиламмония всегда используют все доступные протоны для донора NH – OH2 склеивание. Таким образом, относительная стабилизация ионов метиламмония уменьшается с увеличением количества метильных групп, что объясняет порядок основности воды метиламинов.[4]
Термодинамика
Константа равновесия связана со стандартным Энергия Гиббса изменение для реакции, поэтому для константы диссоциации кислоты
- .
р это газовая постоянная и Т это абсолютная температура. Обратите внимание, что пKа = −log (Kа) и 2.303 ≈ пер (10). При 25 ° C Δграмм⊖ в кДж · моль−1 ≈ 5,708 п.Kа (1 кДж · моль−1 = 1000 джоули на крот ). Бесплатная энергия состоит из энтальпия срок и энтропия срок.[11]
Стандартное изменение энтальпии можно определить по формуле калориметрия или используя уравнение Ван 'т Гоффа, хотя предпочтительнее калориметрический метод. Когда определены и стандартное изменение энтальпии, и константа диссоциации кислоты, стандартное изменение энтропии легко рассчитывается по приведенному выше уравнению. В следующей таблице энтропийные члены рассчитаны из экспериментальных значений pKа и ΔЧАС⊖. Данные были тщательно отобраны и относятся к температуре 25 ° C и нулевой ионной силе в воде.[11]
| Сложный | Равновесие | пKа | Δграмм⊖ (кДж · моль−1)[а] | ΔЧАС⊖ (кДж · моль−1) | −ТΔS⊖ (кДж · моль−1)[b] |
|---|---|---|---|---|---|
| HA = Уксусная кислота | HA ⇌ H+ + А− | 4.756 | 27.147 | −0.41 | 27.56 |
| ЧАС2А+ = Глицин ЧАС+ | ЧАС2А+ ⇌ HA + H+ | 2.351 | 13.420 | 4.00 | 9.419 |
| HA ⇌ H+ + А− | 9.78 | 55.825 | 44.20 | 11.6 | |
| ЧАС2А = Малеиновая кислота | ЧАС2A ⇌ HA− + H+ | 1.92 | 10.76 | 1.10 | 9.85 |
| HA− ⇌ H+ + А2− | 6.27 | 35.79 | −3.60 | 39.4 | |
| ЧАС3А = Лимонная кислота | ЧАС3А ⇌ H2А− + H+ | 3.128 | 17.855 | 4.07 | 13.78 |
| ЧАС2А− ⇌ HA2− + H+ | 4.76 | 27.176 | 2.23 | 24.9 | |
| HA2− ⇌ А3− + H+ | 6.40 | 36.509 | −3.38 | 39.9 | |
| ЧАС3А = Борная кислота | ЧАС3А ⇌ H2А− + H+ | 9.237 | 52.725 | 13.80 | 38.92 |
| ЧАС3А = Фосфорная кислота | ЧАС3А ⇌ H2А− + H+ | 2.148 | 12.261 | −8.00 | 20.26 |
| ЧАС2А− ⇌ HA2− + H+ | 7.20 | 41.087 | 3.60 | 37.5 | |
| HA2− ⇌ А3− + H+ | 12.35 | 80.49 | 16.00 | 54.49 | |
| HA− = Сероводород | HA− ⇌ А2− + H+ | 1.99 | 11.36 | −22.40 | 33.74 |
| ЧАС2А = Щавелевая кислота | ЧАС2A ⇌ HA− + H+ | 1.27 | 7.27 | −3.90 | 11.15 |
| HA− ⇌ А2− + H+ | 4.266 | 24.351 | −7.00 | 31.35 |
| Сложный | Равновесие | пKа | ΔH⊖ (kJ·mol−1) | −ТΔS⊖ (kJ·mol−1) |
|---|---|---|---|---|
| B = Аммиак | HB+ ⇌ B + H+ | 9.245 | 51.95 | 0.8205 |
| B = Метиламин | HB+ ⇌ B + H+ | 10.645 | 55.34 | 5.422 |
| B = Триэтиламин | HB+ ⇌ B + H+ | 10.72 | 43.13 | 18.06 |
The first point to note is that, when pKа is positive, the standard free energy change for the dissociation reaction is also positive. Second, some reactions are экзотермический а некоторые эндотермический, but, when ΔЧАС⊖ отрицательный ТΔS⊖ is the dominant factor, which determines that Δграмм⊖ положительный. Last, the entropy contribution is always unfavourable (ΔS⊖ < 0) in these reactions. Ions in aqueous solution tend to orient the surrounding water molecules, which orders the solution and decreases the entropy. The contribution of an ion to the entropy is the partial molar entropy which is often negative, especially for small or highly charged ions.[56] The ionization of a neutral acid involves formation of two ions so that the entropy decreases (ΔS⊖ < 0). On the second ionization of the same acid, there are now three ions and the anion has a charge, so the entropy again decreases.
Обратите внимание, что стандарт free energy change for the reaction is for the changes из the reactants in their standard states к the products in their standard states. The free energy change в equilibrium is zero since the химические потенциалы of reactants and products are equal at equilibrium.
Experimental determination

The experimental determination of pKа values is commonly performed by means of титрования, in a medium of high ionic strength and at constant temperature.[57] A typical procedure would be as follows. A solution of the compound in the medium is acidified with a strong acid to the point where the compound is fully protonated. The solution is then titrated with a strong base until all the protons have been removed. At each point in the titration pH is measured using a glass electrode и pH meter. The equilibrium constants are found by fitting calculated pH values to the observed values, using the method of наименьших квадратов.[58]
The total volume of added strong base should be small compared to the initial volume of titrand solution in order to keep the ionic strength nearly constant. This will ensure that pKа remains invariant during the titration.
A calculated titration curve for oxalic acid is shown at the right. Oxalic acid has pKа values of 1.27 and 4.27. Therefore, the buffer regions will be centered at about pH 1.3 and pH 4.3. The buffer regions carry the information necessary to get the pKа values as the concentrations of acid and conjugate base change along a buffer region.
Between the two buffer regions there is an end-point, or equivalence point, at about pH 3. This end-point is not sharp and is typical of a diprotic acid whose buffer regions overlap by a small amount: pKа2 − pKа1 is about three in this example. (If the difference in pK values were about two or less, the end-point would not be noticeable.) The second end-point begins at about pH 6.3 and is sharp. This indicates that all the protons have been removed. When this is so, the solution is not buffered and the pH rises steeply on addition of a small amount of strong base. However, the pH does not continue to rise indefinitely. A new buffer region begins at about pH 11 (pKш − 3), which is where самоионизация воды становится важным.
It is very difficult to measure pH values of less than two in aqueous solution with a glass electrode, поскольку Уравнение Нернста breaks down at such low pH values. To determine pK values of less than about 2 or more than about 11 спектрофотометрический[59][60] или же ЯМР[61][62] measurements may be used instead of, or combined with, pH measurements.
When the glass electrode cannot be employed, as with non-aqueous solutions, spectrophotometric methods are frequently used.[37] These may involve поглощение или же флуоресценция измерения. In both cases the measured quantity is assumed to be proportional to the sum of contributions from each photo-active species; with absorbance measurements the Закон Бера-Ламберта is assumed to apply.
Изотермическая калориметрия титрования (ITC) may be used to determine both a pK value and the corresponding standard enthalpy for acid dissociation.[63] Software to perform the calculations is supplied by the instrument manufacturers for simple systems.
Aqueous solutions with normal water cannot be used for 1H NMR measurements but тяжелая вода, D2O, must be used instead. 13C NMR data, however, can be used with normal water and 1H NMR spectra can be used with non-aqueous media. The quantities measured with NMR are time-averaged chemical shifts, as proton exchange is fast on the NMR time-scale. Other chemical shifts, such as those of 31P can be measured.
Микроконстанты

For some molecules, dissociation (or association) can occur at more than one nonequivalent site, and the observed macroscopic equilibrium constant or macroconstant is a combination of microconstants involving distinct species. When one reactant forms two products in parallel, the macroconstant is a sum of two microconstants, . This is true for example for the deprotonation of the аминокислота цистеин, which exists in solution as a neutral цвиттерион HS-CH2-CH(NH3+)-COO−. The two microconstants represent deprotonation either at sulphur or at nitrogen, and the macroconstant sum here is the acid dissociation constant Kа = Kа(-SH) + Kа(-NH3+).[64]
Similarly, a base such as спермин has more than one site where protonation can occur. For example, monoprotonation can occur at a terminal –NH2 group or at internal –NH– groups. В Kб values for dissociation of spermine protonated at one or other of the sites are examples of микроконстанты. They cannot be determined directly by means of pH, absorbance, fluorescence or NMR measurements; a measured Kб value is the sum of the K values for the micro-reactions.
Nevertheless, the site of protonation is very important for biological function, so mathematical methods have been developed for the determination of micro-constants.[65]
When two reactants form a single product in parallel, the macroconstant .[64] For example, the abovementioned equilibrium for spermine may be considered in terms of Kа values of two таутомерный conjugate acids, with macroconstant In this case . This is equivalent to the preceding expression since пропорционально .
When a reactant undergoes two reactions in series, the macroconstant for the combined reaction is the product of the microconstant for the two steps. For example, the abovementioned cysteine zwitterion can lose two protons, one from sulphur and one from nitrogen, and the overall macroconstant for losing two protons is the product of two dissociation constants K = Kа(-SH) Kа(-NH3+).[64] This can also be written in terms of logarithmic constants as pK = pKа(-SH) + pKа(-NH3+).
Applications and significance
A knowledge of pKа values is important for the quantitative treatment of systems involving acid–base equilibria in solution. Many applications exist in биохимия; for example, the pKа values of proteins and аминокислота side chains are of major importance for the activity of enzymes and the stability of proteins.[66] Protein pKа значения cannot always be measured directly, but may be calculated using theoretical methods. Буферные растворы are used extensively to provide solutions at or near the physiological pH for the study of biochemical reactions;[67] the design of these solutions depends on a knowledge of the pKа values of their components. Important buffer solutions include MOPS, which provides a solution with pH 7.2, and tricine, который используется в гель-электрофорез.[68][69] Buffering is an essential part of acid base physiology включая acid–base homeostasis,[70] and is key to understanding disorders such as acid–base imbalance.[71][72][73] В isoelectric point of a given molecule is a function of its pK values, so different molecules have different isoelectric points. This permits a technique called изоэлектрическая фокусировка,[74] which is used for separation of proteins by 2-D gel polyacrylamide gel electrophoresis.
Buffer solutions also play a key role in аналитическая химия. They are used whenever there is a need to fix the pH of a solution at a particular value. Compared with an aqueous solution, the pH of a buffer solution is relatively insensitive to the addition of a small amount of strong acid or strong base. The buffer capacity[75] of a simple buffer solution is largest when pH = pKа. В acid–base extraction, the efficiency of extraction of a compound into an organic phase, such as an эфир, can be optimised by adjusting the pH of the aqueous phase using an appropriate buffer. At the optimum pH, the concentration of the electrically neutral species is maximised; such a species is more soluble in organic solvents having a low диэлектрическая постоянная than it is in water. This technique is used for the purification of weak acids and bases.[76]
А pH indicator is a weak acid or weak base that changes colour in the transition pH range, which is approximately pKа ± 1. The design of a универсальный индикатор requires a mixture of indicators whose adjacent pKа values differ by about two, so that their transition pH ranges just overlap.
В фармакология, ionization of a compound alters its physical behaviour and macro properties such as solubility and липофильность, log п). For example, ionization of any compound will increase the solubility in water, but decrease the lipophilicity. This is exploited in drug development to increase the concentration of a compound in the blood by adjusting the pKа of an ionizable group.[77]
Knowledge of pKа values is important for the understanding of координационные комплексы, which are formed by the interaction of a metal ion, Mm+, действуя как Кислота Льюиса, с лиганд, L, acting as a База Льюиса. However, the ligand may also undergo protonation reactions, so the formation of a complex in aqueous solution could be represented symbolically by the reaction
- [M (H2O)п]м+ + LH ⇌ [M(H2O)п−1L](м−1)+ + H3О+
To determine the equilibrium constant for this reaction, in which the ligand loses a proton, the pKа of the protonated ligand must be known. In practice, the ligand may be polyprotic; Например EDTA4− can accept four protons; in that case, all pKа values must be known. In addition, the metal ion is subject to гидролиз, that is, it behaves as a weak acid, so the pK values for the hydrolysis reactions must also be known.[78]
Оценка опасность associated with an acid or base may require a knowledge of pKа значения.[79] Например, цианистый водород is a very toxic gas, because the цианид-ион inhibits the iron-containing enzyme цитохром с оксидаза. Hydrogen cyanide is a weak acid in aqueous solution with a pKа of about 9. In strongly alkaline solutions, above pH 11, say, it follows that sodium cyanide is "fully dissociated" so the hazard due to the hydrogen cyanide gas is much reduced. An acidic solution, on the other hand, is very hazardous because all the cyanide is in its acid form. Ingestion of cyanide by mouth is potentially fatal, independently of pH, because of the reaction with cytochrome c oxidase.
В наука об окружающей среде acid–base equilibria are important for lakes[80] and rivers;[81][82] Например, humic acids are important components of natural waters. Another example occurs in химическая океанография:[83] in order to quantify the solubility of iron(III) in seawater at various соленость, the pKа values for the formation of the iron(III) hydrolysis products Fe(OH)2+, Fe (ОН)+
2 and Fe(OH)3 were determined, along with the произведение растворимости из гидроксид железа.[84]
Values for common substances
There are multiple techniques to determine the pKа of a chemical, leading to some discrepancies between different sources. Well measured values are typically within 0.1 units of each other. Data presented here were taken at 25 °C in water.[7][85] More values can be found in the Термодинамика section, above. A table of pKа of carbon acids, measured in DMSO, can be found on the page on карбанионы.
| Химическая | Равновесие | пKа |
|---|---|---|
| BH = Аденин | BH ⇌ B− + H+ | 4.17 |
| BH+ 2 ⇌ BH + H+ | 9.65 | |
| ЧАС3А = Мышьяковая кислота | ЧАС3A ⇌ H2А− + H+ | 2.22 |
| ЧАС2А− ⇌ HA2− + H+ | 6.98 | |
| HA2− ⇌ А3− + H+ | 11.53 | |
| HA = Benzoic acid | HA ⇌ H+ + A− | 4.204 |
| HA = Масляная кислота | HA ⇌ H+ + A− | 4.82 |
| ЧАС2А = Хромовая кислота | ЧАС2A ⇌ HA− + H+ | 0.98 |
| HA− ⇌ А2− + H+ | 6.5 | |
| B = Кодеин | BH+ ⇌ B + H+ | 8.17 |
| HA = Крезол | HA ⇌ H+ + A− | 10.29 |
| HA = Муравьиная кислота | HA ⇌ H+ + A− | 3.751 |
| HA = Плавиковая кислота | HA ⇌ H+ + A− | 3.17 |
| HA = Синильная кислота | HA ⇌ H+ + A− | 9.21 |
| HA = Hydrogen selenide | HA ⇌ H+ + A− | 3.89 |
| HA = Пероксид водорода (90%) | HA ⇌ H+ + A− | 11.7 |
| HA = Молочная кислота | HA ⇌ H+ + A− | 3.86 |
| HA = Пропионовая кислота | HA ⇌ H+ + A− | 4.87 |
| HA = Фенол | HA ⇌ H+ + A− | 9.99 |
| ЧАС2А = L-(+)-Ascorbic Acid | ЧАС2A ⇌ HA− + H+ | 4.17 |
| HA− ⇌ А2− + H+ | 11.57 |
Смотрите также
- Ацидоз
- Кислоты в вине: tartaric, яблочный и лимонный are the principal acids in wine.
- Алкалоз
- Газ артериальной крови
- Химическое равновесие
- Электропроводность (электролитическая)
- Grotthuss mechanism: how protons are transferred between hydronium ions and water molecules, accounting for the exceptionally high ionic mobility of the proton (animation).
- Hammett acidity function: a measure of acidity that is used for very concentrated solutions of strong acids, including superacids.
- Ионный транспортный номер
- Закисление океана: dissolution of atmospheric carbon dioxide affects seawater pH. The reaction depends on total inorganic carbon and on solubility equilibria with solid carbonates such as известняк и доломит.
- Закон разбавления
- pCO2
- pH
- Predominance diagram: relates to equilibria involving polyoxyanions. пKа values are needed to construct these diagrams.
- Протонное сродство: a measure of basicity in the gas phase.
- Константы устойчивости комплексов: formation of a complex can often be seen as a competition between proton and metal ion for a ligand, which is the product of dissociation of an acid.
Примечания
- ^ The hydrogen ion does not exist as such in solution. It combines with a solvent molecule; when the solvent is water a гидроксоний ion is formed: H+ + H2O → H3О+. This reaction is quantitative and hence can be ignored in the context of chemical equilibrium
- ^ It is common practice to quote pK values rather than K значения. пK = −log10 K. пKа is often referred to as an acid dissociation constant, but this is, strictly speaking, incorrect as pKа это cologarithm of the dissociation constant.
- ^ It is implicit in this definition that the quotient of коэффициенты активности, , is a constant with a value of 1 under a given set of experimental conditions.
Рекомендации
- ^ Whitten, Kenneth W.; Gailey, Kenneth D.; Davis, Raymond E. (1992). Общая химия (4-е изд.). Издательство колледжа Сондерс. п.660. ISBN 0-03-072373-6.
- ^ Petrucci, Ralph H .; Харвуд, Уильям S .; Herring, F. Geoffrey (2002). Общая химия (8-е изд.). Прентис Холл. стр.667–8. ISBN 0-13-014329-4.
- ^ Perrin DD, Dempsey B, Serjeant EP (1981). "Chapter 3: Methods of pKа Prediction". пKа Prediction for Organic Acids and Bases. (secondary). London: Chapman & Hall. С. 21–26. Дои:10.1007/978-94-009-5883-8. ISBN 978-0-412-22190-3.
- ^ а б Fraczkiewicz R (2013). "In Silico Prediction of Ionization". In Reedijk J (ed.). Reference Module in Chemistry, Molecular Sciences and Chemical Engineering. (secondary). Reference Module in Chemistry, Molecular Sciences and Chemical Engineering [Online]. т. 5. Amsterdam, The Netherlands: Elsevier. Дои:10.1016/B978-0-12-409547-2.02610-X. ISBN 9780124095472.
- ^ Miessler, G. (1991). Неорганическая химия (2-е изд.). Прентис Холл. ISBN 0-13-465659-8. Chapter 6: Acid–Base and Donor–Acceptor Chemistry
- ^ а б Bell, R.P. (1973). The Proton in Chemistry (2-е изд.). London: Chapman & Hall. ISBN 0-8014-0803-2. Includes discussion of many organic Brønsted acids.
- ^ а б c Shriver, D.F; Atkins, P.W. (1999). Неорганическая химия (3-е изд.). Оксфорд: Издательство Оксфордского университета. ISBN 0-19-850331-8. Chapter 5: Acids and Bases
- ^ Housecroft, C.E .; Шарп, А. Г. (2008). Неорганическая химия (3-е изд.). Прентис Холл. ISBN 978-0-13-175553-6. Chapter 6: Acids, Bases and Ions in Aqueous Solution
- ^ Headrick, J.M.; Diken, E.G.; Walters, R. S.; Hammer, N. I.; Christie, R.A.; Cui, J .; Myshakin, E.M.; Duncan, M.A.; Johnson, M.A.; Jordan, K.D. (2005). "Spectral Signatures of Hydrated Proton Vibrations in Water Clusters". Наука. 308 (5729): 1765–69. Bibcode:2005Sci...308.1765H. Дои:10.1126/science.1113094. PMID 15961665. S2CID 40852810.
- ^ Smiechowski, M.; Stangret, J. (2006). "Proton hydration in aqueous solution: Fourier transform infrared studies of HDO spectra". J. Chem. Phys. 125 (20): 204508–204522. Bibcode:2006JChPh.125t4508S. Дои:10.1063/1.2374891. PMID 17144716.
- ^ а б c Goldberg, R.; Kishore, N.; Lennen, R. (2002). "Thermodynamic Quantities for the Ionization Reactions of Buffers" (PDF). J. Phys. Chem. Ref. Данные. 31 (2): 231–370. Bibcode:2002JPCRD..31..231G. Дои:10.1063/1.1416902. Архивировано из оригинал (PDF) на 2008-10-06.
- ^ Jolly, William L. (1984). Современная неорганическая химия. Макгроу-Хилл. стр.198. ISBN 978-0-07-032760-3.
- ^ Burgess, J. (1978). Ионы металлов в растворе. Эллис Хорвуд. ISBN 0-85312-027-7. Section 9.1 "Acidity of Solvated Cations" lists many pKа значения.
- ^ Petrucci, R.H.; Harwood, R.S.; Herring, F.G. (2002). Общая химия (8-е изд.). Прентис Холл. ISBN 0-13-014329-4. p.698
- ^ а б c Rossotti, F.J.C.; Rossotti, H. (1961). The Determination of Stability Constants. Макгроу – Хилл. Chapter 2: Activity and Concentration Quotients
- ^ «Проект: поправки на ионную силу для констант стабильности». Международный союз теоретической и прикладной химии. Получено 2019-03-28.
- ^ Аткинс, P.W .; де Паула, Дж. (2006). Физическая химия. Издательство Оксфордского университета. ISBN 0-19-870072-5. Section 7.4: The Response of Equilibria to Temperature
- ^ Petrucci, Ralph H .; Харвуд, Уильям S .; Herring, F. Geoffrey (2002). Общая химия: принципы и современные приложения (8-е изд.). Прентис Холл. п.633. ISBN 0-13-014329-4.
Are you wondering... How using activities makes the equilibrium constant dimensionless?
- ^ Shriver, D.F; Atkins, P.W. (1999). Неорганическая химия (3-е изд.). Издательство Оксфордского университета. ISBN 0-19-850331-8. Раздел 5.1c Strong and weak acids and bases
- ^ Porterfield, William W. (1984). Неорганическая химия. Эддисон-Уэсли. п. 260. ISBN 0-201-05660-7.
- ^ а б Shriver, D.F; Atkins, P.W. (1999). Неорганическая химия (3-е изд.). Издательство Оксфордского университета. ISBN 0-19-850331-8. Раздел 5.2 Solvent leveling
- ^ Levanov, A. V.; Isaikina, O. Ya.; Lunin, V. V. (2017). "Dissociation constant of nitric acid". Российский журнал физической химии А. 91 (7): 1221–1228. Bibcode:2017RJPCA..91.1221L. Дои:10.1134/S0036024417070196. S2CID 104093297.
- ^ Трумаль, Александр; Липпинг, Лаури; Кальюранд, Ивари; Koppel, Ilmar A .; Лейто, Иво (2016). «Кислотность сильных кислот в воде и диметилсульфоксиде». The Journal of Physical Chemistry A. 120 (20): 3663–3669. Bibcode:2016JPCA..120.3663T. Дои:10.1021 / acs.jpca.6b02253. PMID 27115918.
- ^ Mehta, Akul (22 October 2012). "Henderson–Hasselbalch Equation: Derivation of pKа и рKб". PharmaXChange. Получено 16 ноября 2014.
- ^ The values are for 25 °C and 0 ionic strength – Пауэлл, Киптон Дж .; Brown, Paul L .; Бирн, Роберт Х .; Гайда, Тамаш; Хефтер, Гленн; Sjöberg, Staffan; Ваннер, Ханс (2005). "Химический состав экологически значимых тяжелых металлов с неорганическими лигандами. Часть 1: Hg2+, Cl−, ОЙ−, CO2−
3, ТАК2−
4, и PO3−
4 водные системы ». Pure Appl. Chem. 77 (4): 739–800. Дои:10.1351 / pac200577040739. - ^ Brown, T.E.; Lemay, H.E.; Bursten, B.E.; Murphy, C.; Woodward, P. (2008). Химия: центральная наука (11-е изд.). Нью-Йорк: Прентис-Холл. п. 689. ISBN 978-0-13-600617-6.
- ^ а б Greenwood, N.N .; Эрншоу, А. (1997). Химия элементов (2-е изд.). Оксфорд: Баттерворт-Хайнеманн. п. 50. ISBN 0-7506-3365-4.
- ^ а б c Miessler, Gary L.; Tarr Donald A. (1999). Неорганическая химия (2-е изд.). Прентис Холл. п. 164. ISBN 0-13-465659-8.
- ^ а б Хухи, Джеймс Э. (1983). Неорганическая химия (3-е изд.). Харпер и Роу. п. 297. ISBN 0-06-042987-9.
- ^ Lide, D.R. (2004). CRC Handbook of Chemistry and Physics, Student Edition (84-е изд.). CRC Press. ISBN 0-8493-0597-7. Section D–152
- ^ Skoog, Douglas A.; West, Donald M .; Holler, F. James; Crouch, Stanley R. (2014). Основы аналитической химии (9-е изд.). Брукс / Коул. п. 212. ISBN 978-0-495-55828-6.
- ^ Housecroft, C.E .; Шарп, А. Г. (2004). Неорганическая химия (2-е изд.). Прентис Холл. п. 163. ISBN 978-0-13-039913-7.
- ^ Harned, H.S.; Owen, B.B (1958). The Physical Chemistry of Electrolytic Solutions. New York: Reinhold Publishing Corp. pp.634 –649, 752–754.
- ^ а б c d Loudon, G. Marc (2005), Органическая химия (4th ed.), New York: Oxford University Press, pp. 317–318, ISBN 0-19-511999-1
- ^ Марч, Дж.; Smith, M. (2007). Продвинутая органическая химия (6-е изд.). Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-72091-1. Chapter 8: Acids and Bases
- ^ Kütt, A .; Movchun, V.; Rodima, T; Dansauer, T.; Rusanov, E.B.; Leito, I .; Кальюранд, I .; Koppel, J.; Pihl, V .; Koppel, I .; Овсянников, Г .; Toom, L.; Mishima, M.; Medebielle, M.; Lork, E.; Röschenthaler, G-V.; Koppel, I.A.; Kolomeitsev, A.A. (2008). "Pentakis(trifluoromethyl)phenyl, a Sterically Crowded and Electron-withdrawing Group: Synthesis and Acidity of Pentakis(trifluoromethyl)benzene, -toluene, -phenol, and -aniline". J. Org. Chem. 73 (7): 2607–2620. Дои:10.1021/jo702513w. PMID 18324831.
- ^ а б Kütt, A .; Leito, I .; Кальюранд, I .; Sooväli, L .; Vlasov, V.M.; Yagupolskii, L.M.; Koppel, I.A. (2006). "A Comprehensive Self-Consistent Spectrophotometric Acidity Scale of Neutral Brønsted Acids in Acetonitrile". J. Org. Chem. 71 (7): 2829–2838. Дои:10.1021/jo060031y. PMID 16555839.
- ^ Кальюранд, I .; Kütt, A .; Sooväli, L .; Родима, Т .; Мяэметс, В .; Leito, I; Koppel, I.A. (2005).«Расширение самосогласованной спектрофотометрической шкалы основности в ацетонитриле до полного диапазона 28 единиц pKa: объединение различных шкал основности». J. Org. Chem. 70 (3): 1019–1028. Дои:10.1021 / jo048252w. PMID 15675863.
- ^ «Таблица Bordwell pKa (Кислотность в ДМСО)». Архивировано из оригинал 9 октября 2008 г.. Получено 2008-11-02.
- ^ Housecroft, C.E .; Шарп, А. Г. (2008). Неорганическая химия (3-е изд.). Прентис Холл. ISBN 978-0-13-175553-6. Глава 8: Неводные среды
- ^ Рочестер, C.H. (1970). Функции кислотности. Академическая пресса. ISBN 0-12-590850-4.
- ^ Olah, G.A; Пракаш, S; Соммер, Дж (1985). Суперкислоты. Нью-Йорк: Wiley Interscience. ISBN 0-471-88469-3.
- ^ Coetzee, J.F .; Падманабхан, Г. (1965). «Протоноакцепторная сила и гомоконъюгирование моно- и диаминов». Варенье. Chem. Soc. 87 (22): 5005–5010. Дои:10.1021 / ja00950a006.
- ^ Pine, S.H .; Хендриксон, J.B .; Cram, D.J .; Хаммонд, Г.С. (1980). Органическая химия. Макгроу – Хилл. п. 203. ISBN 0-07-050115-7.
- ^ Box, K.J .; Völgyi, G .; Ruiz, R .; Comer, J.E .; Такач-Новак, К .; Bosch, E .; Ràfols, C .; Розес, М. (2007). «Физико-химические свойства новой многокомпонентной системы сорастворителей для определения pKa плохо растворимых фармацевтических соединений». Helv. Чим. Acta. 90 (8): 1538–1553. Дои:10.1002 / hlca.200790161.
- ^ а б Housecroft, Catherine E .; Шарп, Алан Г. (2005). Неорганическая химия (2-е изд.). Харлоу, Великобритания: Pearson Prentice Hall. С. 170–171. ISBN 0-13-039913-2.
- ^ а б Дуглас Б., МакДэниел Д.Х. и Александр Дж. Дж. Концепции и модели неорганической химии (2-е изд. Wiley 1983) с.526. ISBN 0-471-21984-3
- ^ Полинг, Л. (1960). Природа химической связи и строение молекул и кристаллов; введение в современную структурную химию (3-е изд.). Итака (Нью-Йорк): Издательство Корнельского университета. п.277. ISBN 0-8014-0333-2.
- ^ Pine, S.H .; Хендриксон, J.B .; Cram, D.J .; Хаммонд, Г.С. (1980). Органическая химия. Макгроу – Хилл. ISBN 0-07-050115-7. Раздел 13-3: Количественные корреляции эффектов заместителей (Часть B) - Уравнение Хэммета
- ^ Хэммет, Л.П. (1937). «Влияние структуры на реакции органических соединений. Производные бензола». Варенье. Chem. Soc. 59 (1): 96–103. Дои:10.1021 / ja01280a022.
- ^ Hansch, C .; Лев, А .; Taft, R. W. (1991). "Обзор констант заместителей Хэммета и резонансных и полевых параметров". Chem. Rev. 91 (2): 165–195. Дои:10.1021 / cr00002a004.
- ^ Короче, J (1997). «Составление и критическая оценка параметров и уравнений структурной реактивности: Часть 2. Расширение шкалы Хаммета σ за счет данных для ионизации замещенных бензойных кислот в водных растворителях при 25 ° C (Технический отчет)». Чистая и прикладная химия. 69 (12): 2497–2510. Дои:10.1351 / pac199769122497. S2CID 98814841.
- ^ Pine, S.H .; Хендриксон, J.B .; Cram, D.J .; Хаммонд, Г.С. (1980). Органическая химия. Макгроу – Хилл. ISBN 0-07-050115-7. Раздел 6-2: Структурное влияние на кислотность и основность
- ^ Alder, R.W .; Bowman, P.S .; Стил, W.R.S .; Винтерман, Д. (1968). «Замечательная основность 1,8-бис (диметиламино) нафталина». Chem. Commun. (13): 723–724. Дои:10.1039 / C19680000723.
- ^ Алдер, Р.В. (1989). «Влияние деформации на основность амина». Chem. Rev. 89 (5): 1215–1223. Дои:10.1021 / cr00095a015.
- ^ Аткинс, Питер Уильям; Де Паула, Хулио (2006). Физическая химия Аткинса. Нью-Йорк: У. Фриман. п.94. ISBN 978-0-7167-7433-4.
- ^ Martell, A.E .; Мотекайтис, Р.Дж. (1992). Определение и использование констант устойчивости. Вайли. ISBN 0-471-18817-4. Глава 4: Экспериментальная процедура для потенциометрии pH Измерение равновесия металлических комплексов
- ^ Леггетт, Д.Дж. (1985). Вычислительные методы определения констант формации. Пленум. ISBN 0-306-41957-2.
- ^ Allen, R.I .; Box, K.J .; Comer, J.E.A .; Peake, C .; Там, К. (1998). «Многоволновое спектрофотометрическое определение констант кислотной диссоциации ионизируемых лекарственных средств». J. Pharm. Биомед. Анальный. 17 (4–5): 699–712. Дои:10.1016 / S0731-7085 (98) 00010-7. PMID 9682153.
- ^ Box, K.J .; Donkor, R.E .; Jupp, P.A .; Лидер, И.П .; Trew, D.F .; Тернер, Ч. (2008). «Химия мульти-протонных лекарств, часть 1: потенциометрическое, многоволновое УФ- и ЯМР-pH-титриметрическое исследование микропроцессов SKI-606». J. Pharm. Биомед. Анальный. 47 (2): 303–311. Дои:10.1016 / j.jpba.2008.01.015. PMID 18314291.
- ^ Попов, К .; Ronkkomaki, H .; Lajunen, L.H.J. (2006). "Рекомендации по измерениям ЯМР для определения высокого и низкого pKа Значения" (PDF). Pure Appl. Chem. 78 (3): 663–675. Дои:10.1351 / pac200678030663. S2CID 4823180.
- ^ Szakács, Z .; Хэгеле, Г. (2004). «Точное определение низких значений pK титрованием 1H ЯМР». Таланта. 62 (4): 819–825. Дои:10.1016 / j.talanta.2003.10.007. PMID 18969368.
- ^ Фейг, Эндрю Л., изд. (2016). «Методы энзимологии». Калориметрия. Эльзевир. 567: 2–493. ISSN 0076-6879.
- ^ а б c Splittgerber, A. G .; Чинандер, Л.Л. (1 февраля 1988 г.). «Спектр диссоциации промежуточного цистеина: биофизический химический эксперимент». Журнал химического образования. 65 (2): 167. Bibcode:1988JChEd..65..167S. Дои:10.1021 / ed065p167.
- ^ Frassineti, C .; Алдериги, L; Ганс, П; Сабатини, А; Vacca, A; Гелли, С. (2003). «Определение констант протонирования некоторых фторированных полиаминов с помощью 13Данные C ЯМР обработаны новой компьютерной программой HypNMR2000. Последовательность протонирования в полиаминах ». Анальный. Биоанал. Chem. 376 (7): 1041–1052. Дои:10.1007 / s00216-003-2020-0. PMID 12845401. S2CID 14533024.
- ^ Онуфриев А .; Case, D.A; Ульманн Г.М. (2001). «Новый взгляд на определение pH в биомолекулах». Биохимия. 40 (12): 3413–3419. Дои:10.1021 / bi002740q. PMID 11297406.
- ^ Хорошо, н.э .; Winget, G.D .; Зима, Вт .; Connolly, T.N .; Идзава, S .; Сингх, Р.М.М. (1966). «Буферы с ионами водорода для биологических исследований». Биохимия. 5 (2): 467–477. Дои:10.1021 / bi00866a011. PMID 5942950.
- ^ Данн, М.Дж. (1993). Гель-электрофорез: белки. Bios Scientific Publishers. ISBN 1-872748-21-X.
- ^ Мартин, Р. (1996). Гель-электрофорез: нуклеиновые кислоты. Bios Scientific Publishers. ISBN 1-872748-28-7.
- ^ Brenner, B.M .; Stein, J.H., ред. (1979). Кислотно-щелочной и калиевый гомеостаз. Черчилль Ливингстон. ISBN 0-443-08017-8.
- ^ Скорпион, Р. (2000). Основы кислот, оснований, буферов и их применения в биохимических системах. Kendall / Hunt Pub. Co. ISBN 0-7872-7374-0.
- ^ Beynon, R.J .; Истерби, Дж. (1996). Буферные решения: основы. Оксфорд: Издательство Оксфордского университета. ISBN 0-19-963442-4.
- ^ Perrin, D.D .; Демпси, Б. (1974). Буферы для контроля pH и ионов металлов. Лондон: Чепмен и Холл. ISBN 0-412-11700-2.
- ^ Гарфин, Д .; Ахуджа, С., ред. (2005). Справочник по изоэлектрической фокусировке и протеомике. 7. Эльзевир. ISBN 0-12-088752-5.
- ^ Хуланицки А. (1987). Реакции кислот и оснований в аналитической химии. Массон, М.Р. (редактор переводов). Хорвуд. ISBN 0-85312-330-6.
- ^ Эйал, А.М. (1997). «Кислотная экстракция экстрагентами, связанными с кислотой и основанием». Ионный обмен и экстракция растворителем: ряд достижений. 13: 31–94.
- ^ Авдеф, А. (2003). Абсорбция и разработка лекарств: растворимость, проницаемость и состояние заряда. Нью-Йорк: Вили. ISBN 0-471-42365-3.
- ^ Beck, M.T .; Надьпал, И. (1990). Химия сложных равновесий. Хорвуд. ISBN 0-85312-143-5.
- ^ van Leeuwen, C.J .; Герменс, Л. М. (1995). Оценка риска химических веществ: введение. Springer. С. 254–255. ISBN 0-7923-3740-9.
- ^ Скуг, Д.А.; West, D.M .; Holler, J.F .; Крауч, С. (2004). Основы аналитической химии (8-е изд.). Томсон Брукс / Коул. ISBN 0-03-035523-0. Глава 9-6: Кислотный дождь и буферная емкость озер
- ^ Штумм, В .; Морган, Дж. Дж. (1996). Химия воды. Нью-Йорк: Вили. ISBN 0-471-05196-9.
- ^ Сноэинк, В.Л .; Дженкинс, Д. (1980). Химия воды: химическое равновесие и скорость в природных водах. Нью-Йорк: Вили. ISBN 0-471-51185-4.
- ^ Миллеро, Ф.Дж. (2006). Химическая океанография (3-е изд.). Лондон: Тейлор и Фрэнсис. ISBN 0-8493-2280-4.
- ^ Millero, F.J .; Лю, X. (2002). «Растворимость железа в морской воде». Морская химия. 77 (1): 43–54. Дои:10.1016 / S0304-4203 (01) 00074-3.
- ^ Спейт, Дж. (2005). Справочник Ланге по химии (18-е изд.). Макгроу – Хилл. ISBN 0-07-143220-5. Глава 8
дальнейшее чтение
- Альберт, А .; Сержант, Э. (1971). Определение констант ионизации: лабораторное руководство. Чепмен и Холл. ISBN 0-412-10300-1. (Предыдущее издание опубликовано как Константы ионизации кислот и оснований. Лондон (Великобритания): Метуэн. 1962 г.)
- Аткинс, P.W .; Джонс, Л. (2008). Химические принципы: поиски понимания (4-е изд.). W.H. Фримен. ISBN 978-1-4292-0965-6.
- Housecroft, C.E .; Шарп, А. Г. (2008). Неорганическая химия (3-е изд.). Прентис Холл. ISBN 978-0-13-175553-6. (Неводные растворители)
- Хуланицки А. (1987). Реакции кислот и оснований в аналитической химии. Хорвуд. ISBN 0-85312-330-6. (редактор перевода: Мэри Р. Массон)
- Perrin, D.D .; Демпси, Б .; Сержант, Э. (1981). Прогноз pKa для органических кислот и оснований. Чепмен и Холл. ISBN 0-412-22190-X.
- Райхардт, К. (2003). Растворители и их действие в органической химии (3-е изд.). Wiley-VCH. ISBN 3-527-30618-8. Глава 4: Влияние растворителя на положение гомогенного химического равновесия.
- Skoog, D.A .; West, D.M .; Holler, J.F .; Крауч, С. (2004). Основы аналитической химии (8-е изд.). Томсон Брукс / Коул. ISBN 0-03-035523-0.
внешняя ссылка
- Данные о кислотности и щелочности в неводных растворителях Обширная библиография pKа ценности в ДМСО, ацетонитрил, THF, гептан, 1,2-дихлорэтан, а в газовой фазе
- Curtipot Универсальное бесплатное программное обеспечение для расчета pH и кислотно-щелочного равновесия, а также для моделирования и анализа потенциометрическое титрование кривые с электронными таблицами
- Калькулятор физических / химических свойств SPARC Включает базу данных с водной, неводной и газовой фазой pKа значения, которые можно найти с помощью Улыбки или же Регистрационные номера CAS
- Константы водного равновесия пKа значения для различных кислот и оснований. Включает таблицу некоторых продуктов растворимости
- Бесплатное руководство по pKа и журнал п интерпретация и измерение Объяснение значения этих свойств для фармакология
- Бесплатный инструмент онлайн-прогнозов (Марвин) пKа, бревно п, бревно d и т. д. от ChemAxon
- Chemicalize.org:Список прогнозируемых свойств на основе структуры
- Эванс П.Kа Диаграмма [1]



![{ Displaystyle К _ { текст {a}} = mathrm { frac {[A ^ {-}] [H ^ {+}]} {[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa9f960c87ed3dbf034fd4671dcb775e4efb7072)
![{ displaystyle mathrm {p} K _ { ce {a}}} = - log _ {10} K _ { text {a}} = log _ {10} { frac {{ ce {[ HA]}}} {[{ ce {A ^ -}}] [{ ce {H +}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7af05bf129db2f9bc618fe809660b6e4ff8dce9)


![{ displaystyle K ^ { ominus} = {{ frac {[{ ce {A ^ -}}] [{ ce {H +}}]} {{ ce {[HA]}}}} Gamma }, quad Gamma = { frac { gamma _ {{ ce {A ^ -}}} gamma _ {{ ce {H +}}}} { gamma _ {{ ce {HA} }} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e9373db7091aeb4f51a26757a677b420f0a8418)

![{ displaystyle K _ { text {a}} = { frac {K ^ { ominus}} { Gamma}} = mathrm { frac {[A ^ {-}] [H ^ {+}]} {[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a5a59c740de89347ec4c96d982292fc05c64b2f)
![{ displaystyle mathrm {p} K _ { ce {a}}} = - log _ {10} { frac {[{ ce {A ^ -}}] [{ ce {H ^ +} }]} {[{ ce {HA}}]}} = log _ {10} { frac {{ ce {[HA]}}} {[{ ce {A ^ -}}] [{ ce {H +}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bed5fbab82167a42994a6d735931d08b06f1e7a5)



![{ displaystyle beta _ {2} = { frac {{ ce {[H_2A]}}} {[{ ce {A ^ {2 -}}}] [{ ce {H +}}] ^ { 2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3306fbf9ccf8d12352eab96dfb5461897f2c3a15)


![{ displaystyle K _ { text {disoc}} = mathrm { frac {[A ^ {-}] [H ^ {+}]} {[HA]}}: mathrm {p} K _ { text { a}} = - log K _ { text {disoc}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5f9c1efd45de9edf690ebf6a72cc806eb2b0331)
![{ displaystyle K _ { text {assoc}} = mathrm { frac {[HA]} {[A ^ {-}] [H ^ {+}]}}: mathrm {p} K _ { text { b}} = - log K _ { text {assoc}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a0453338b1d420214ac7c127d3faa13374fce0)






![{ Displaystyle К _ { mathrm {a}} = mathrm { frac {[A ^ {-}] [H ^ {+}]} {[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df1424aa532585fc7ad6dd660a596705ee31a2b)







![{ displaystyle mathrm {pH} = mathrm {p} K _ { text {a}} + log mathrm { frac {[A ^ {-}]} {[HA]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e874f2b8ea8e4127605788c356393cfd7fff37)
![{ displaystyle mathrm {p} K _ { ce {a1}}} = log _ {10} { frac {[{ ce {H_3PO_4}}]} {[{ ce {H_2PO_4 ^ {-} }}] [{ ce {H ^ +}}]}} = 2,14}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff6e67381cb8a691b8873fbf884dad30b001352)
![{ displaystyle mathrm {p} K _ { ce {a2}}} = log _ {10} { frac {[{ ce {H_2PO_4 ^ {-}}}]} {[{ ce {HPO_4 ^ {2 -}}}] [{ ce {H ^ +}}]}} = 7.2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efe9f5a620a62c8de4a6567f58faf01e66829903)
![{ displaystyle mathrm {p} K _ { ce {a3}}} = log _ {10} { frac {[{ ce {HPO_4 ^ {2 -}}}]} {[{ ce { PO_4 ^ {3 -}}}] [{ ce {H ^ +}}]}} = 12,37}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf6cf97c1d47ba55db3a383374b9d8cd4eda22ee)





![{ displaystyle { begin {align} K _ { text {b}} & = mathrm { frac {[HB ^ {+}] [OH ^ {-}]} {[B]}} mathrm {p} K _ { text {b}} & = - log _ {10} left (K _ { text {b}} right) end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dea1aac629a595476e18c042a8f4365a50f0efc)
![{ displaystyle mathrm {[OH ^ {-}]} = { frac {K _ { mathrm {w}}} { mathrm {[H ^ {+}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7f583da9f8b50145990ffa4342919930edfa16)
![{ displaystyle K _ { text {b}} = { frac {[ mathrm {HB ^ {+}}] K _ { text {w}}} { mathrm {[B] [H ^ {+}] }}} = { frac {K _ { text {w}}} {K _ { text {a}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/921c3abd37a1c5c00c31831509d3b090394c0d47)


![{ Displaystyle К _ { mathrm {b}} = mathrm { frac {[M_ {p} (OH) _ {q-1}] [OH]} {[M_ {p} (OH) _ {q} ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cbfccb80ce8c2075e5423896b4c90d23fc7f8ef)
![{ displaystyle K _ { text {a}} = mathrm { frac {[H ^ {+}] [OH ^ {-}]} {[H_ {2} O]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdc540ad193c8f1661c1897698be93153fc5fb84)
![{ Displaystyle К _ { текст {w}} = [ mathrm {H} ^ {+}] [ mathrm {OH} ^ {-}] ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0039f77db244ea2f6d03d3475dc7a232a8ccb16)









