Гауссовский процесс - Gaussian process

В теория вероятности и статистика, а Гауссовский процесс это случайный процесс (набор случайных величин, проиндексированных по времени или пространству), так что каждый конечный набор этих случайных величин имеет многомерное нормальное распределение, т.е. каждое конечное линейная комбинация из них нормально распространяется. Распределение гауссовского процесса - это совместное распределение всех этих (бесконечно многих) случайных величин, и как таковое, это распределение по функциям с непрерывной областью определения, например время или пространство.

Алгоритм машинного обучения, включающий гауссовский процесс, использует ленивое обучение и мера сходства между точками ( функция ядра), чтобы предсказать значение невидимой точки из обучающих данных. Прогноз - это не только оценка для этой точки, но и информация о неопределенности - это одномерное распределение Гаусса.^[1]Для прогнозирования с несколькими выходами многомерные гауссовские процессы^[2][3] используются, для которых многомерное распределение Гаусса - предельное распределение в каждой точке.

Для некоторых функций ядра матричная алгебра может использоваться для вычисления прогнозов с использованием техники кригинг. Когда используется параметризованное ядро, программное обеспечение оптимизации обычно используется для соответствия гауссовской модели процесса.

Концепция гауссовских процессов названа в честь Карл Фридрих Гаусс поскольку он основан на понятии гауссова распределения (нормальное распределение ). Гауссовские процессы можно рассматривать как бесконечномерное обобщение многомерных нормальных распределений.

Гауссовские процессы полезны в статистическое моделирование, используя свойства, унаследованные от нормального распределения. Например, если случайный процесс моделируется как гауссовский процесс, распределения различных производных величин могут быть получены явно. Такие величины включают среднее значение процесса за определенный период времени и ошибку при оценке среднего значения с использованием значений выборки за небольшой набор времен. Хотя точные модели часто плохо масштабируются по мере увеличения объема данных, несколько методы аппроксимации были разработаны, которые часто сохраняют хорошую точность, резко сокращая время вычислений.

Определение

Время непрерывное случайный процесс ${ displaystyle left {X_ {t}; т in T right }}$ гауссовский если и только если для каждого конечный набор из индексы ${ displaystyle t_ {1}, ldots, t_ {k}}$ в индексном наборе ${ displaystyle T}$

${ displaystyle mathbf {X} _ {t_ {1}, ldots, t_ {k}} = (X_ {t_ {1}}, ldots, X_ {t_ {k}})}$

это многомерный гауссовский случайная переменная.^[4] Это то же самое, что сказать любую линейную комбинацию ${ displaystyle (X_ {t_ {1}}, ldots, X_ {t_ {k}})}$ имеет одномерное нормальное (или гауссово) распределение.

С помощью характеристические функции случайных величин свойство Гаусса можно сформулировать следующим образом: ${ displaystyle left {X_ {t}; т in T right }}$ гауссовский тогда и только тогда, когда для каждого конечного набора индексов ${ displaystyle t_ {1}, ldots, t_ {k}}$, есть ценные ${ displaystyle sigma _ { ell j}}$, ${ displaystyle mu _ { ell}}$ с ${ displaystyle sigma _ {jj}> 0}$ такое, что для всех ${ displaystyle s_ {1}, s_ {2}, ldots, s_ {k} in mathbb {R}}$

${ displaystyle operatorname {E} left ( exp left (я сумма _ { ell = 1} ^ {k} s _ { ell} mathbf {X} _ {t _ { ell}} right) right) = exp left (- { frac {1} {2}} , sum _ { ell, j} sigma _ { ell j} s _ { ell} s_ {j } + i sum _ { ell} mu _ { ell} s _ { ell} right)}$.

куда ${ displaystyle i}$ обозначает мнимая единица такой, что ${ displaystyle i ^ {2} = - 1}$.

Цифры ${ displaystyle sigma _ { ell j}}$ и ${ displaystyle mu _ { ell}}$ можно показать как ковариации и средства переменных в процессе.^[5]

Дисперсия

Дисперсия гауссовского процесса конечна в любое время ${ displaystyle t}$, формально^{[6]:п. 515}

${ displaystyle operatorname {var} [X (t)] = operatorname {E} [| X (t) - operatorname {E} [X (t)] | ^ {2}] < infty quad { text {для всех}} t in T}$.

Стационарность

Для общих случайных процессов стационарность в строгом смысле слова подразумевает стационарность в широком смысле но не всякий стационарный случайный процесс в широком смысле является стационарным в строгом смысле слова. Однако для гауссовского случайного процесса эти две концепции эквивалентны.^{[6]:п. 518}

Гауссовский случайный процесс является стационарным в строгом смысле слова тогда и только тогда, когда он стационарен в широком смысле.

Пример

Есть явное представление для стационарных гауссовских процессов.^[7] Простой пример этого представления:

${ Displaystyle X_ {t} = соз (at) xi _ {1} + sin (at) xi _ {2}}$

куда ${ displaystyle xi _ {1}}$ и ${ displaystyle xi _ {2}}$ независимые случайные величины с стандартное нормальное распределение.

Ковариационные функции

Ключевым фактом гауссовских процессов является то, что они могут быть полностью определены их статистикой второго порядка.^[8] Таким образом, если предположить, что гауссовский процесс имеет нулевое среднее значение, определение ковариационная функция полностью определяет поведение процесса. Важно отметить, что неотрицательная определенность этой функции дает возможность ее спектрального разложения с использованием Расширение Карунена – Лоэва. Основные аспекты, которые могут быть определены с помощью функции ковариации, - это процесс стационарность, изотропия, гладкость и периодичность.^[9][10]

Стационарность относится к поведению процесса относительно разделения любых двух точек ${ displaystyle x}$ и ${ displaystyle x '}$. Если процесс стационарный, это зависит от их разделения, ${ displaystyle x-x '}$, а если он нестационарный, это зависит от фактического положения точек ${ displaystyle x}$ и ${ displaystyle x '}$. Например, частный случай Процесс Орнштейна – Уленбека, а Броуновское движение процесс, является стационарным.

Если процесс зависит только от ${ Displaystyle | х-х '|}$, евклидово расстояние (не направление) между ${ displaystyle x}$ и ${ displaystyle x '}$, то процесс считается изотропным. Процесс, который одновременно является стационарным и изотропным, считается однородный;^[11] на практике эти свойства отражают различия (или, скорее, их отсутствие) в поведении процесса с учетом местоположения наблюдателя.

В конечном итоге гауссовские процессы переводятся как априорные функции, и гладкость этих априорных значений может быть индуцирована ковариационной функцией.^[9] Если мы ожидаем, что для "близких" точек ввода ${ displaystyle x}$ и ${ displaystyle x '}$ их соответствующие выходные точки ${ displaystyle y}$ и ${ displaystyle y '}$ быть "рядом" тоже, то предположение о непрерывности присутствует. Если мы хотим учесть значительное смещение, мы могли бы выбрать более грубую ковариационную функцию. Крайними примерами такого поведения являются ковариационная функция Орнштейна – Уленбека и квадрат экспоненты, где первая никогда не дифференцируема, а вторая - бесконечно дифференцируема.

Под периодичностью понимается создание периодических закономерностей в поведении процесса. Формально это достигается отображением входных данных ${ displaystyle x}$ в двумерный вектор ${ Displaystyle и (х) = влево ( соз (х), грех (х) вправо)}$.

Обычные ковариационные функции

Влияние выбора различных ядер на априорное распределение функций гауссовского процесса. Слева - квадрат экспоненциального ядра. Средний - броуновский. Правый квадратичный.

Существует ряд общих ковариационных функций:^[10]

• Постоянный : ${ Displaystyle К _ { OperatorName {C}} (х, х ') = С}$
• Линейный: ${ Displaystyle К _ { OperatorName {L}} (х, х ') = х ^ {Т} х'}$
• белый гауссов шум: ${ displaystyle K _ { operatorname {GN}} (x, x ') = sigma ^ {2} delta _ {x, x'}}$
• Квадрат экспоненты: ${ displaystyle K _ { operatorname {SE}} (x, x ') = exp { Big (} - { frac {| d | ^ {2}} {2 ell ^ {2}}} { Большой )}}$
• Орнштейн – Уленбек: ${ displaystyle K _ { operatorname {OU}} (x, x ') = exp left (- { frac {| d |} { ell}} right)}$
• Матерн: ${ displaystyle K _ { operatorname {Matern}} (x, x ') = { frac {2 ^ {1- nu}} { Gamma ( nu)}} { Big (} { frac {{ sqrt {2 nu}} | d |} { ell}} { Big)} ^ { nu} K _ { nu} { Big (} { frac {{ sqrt {2 nu}} | d |} { ell}} { Big)}}$
• Периодический: ${ displaystyle K _ { operatorname {P}} (x, x ') = exp left (- { frac {2 sin ^ {2} left ({ frac {d} {2}} right )} { ell ^ {2}}} right)}$
• Рациональный квадратичный: ${ displaystyle K _ { operatorname {RQ}} (x, x ') = (1+ | d | ^ {2}) ^ {- alpha}, quad alpha geq 0}$

Здесь ${ displaystyle d = x-x '}$. Параметр ${ displaystyle ell}$ - характерный масштаб процесса (практически «насколько близко» две точки ${ displaystyle x}$ и ${ displaystyle x '}$ должны существенно влиять друг на друга), ${ displaystyle delta}$ это Дельта Кронекера и ${ displaystyle sigma}$ в стандартное отклонение шумовых колебаний. Более того, ${ displaystyle K _ { nu}}$ это модифицированная функция Бесселя порядка ${ displaystyle nu}$ и ${ Displaystyle Гамма ( ню)}$ это гамма-функция оценивается в ${ displaystyle nu}$. Важно отметить, что сложная ковариационная функция может быть определена как линейная комбинация других более простых ковариационных функций для включения различных представлений о доступном наборе данных.

Ясно, что выводимые результаты зависят от значений гиперпараметров. ${ displaystyle theta}$ (например. ${ displaystyle ell}$ и ${ displaystyle sigma}$), определяющие поведение модели. Популярный выбор для ${ displaystyle theta}$ должен предоставить максимум апостериори (MAP) оценки этого с некоторыми выбранными предварительными. Если априор очень близок к однородному, это то же самое, что и максимизация предельная вероятность процесса; маргинализация осуществляется по наблюдаемым значениям процесса ${ displaystyle y}$.^[10] Этот подход также известен как максимальная вероятность II, максимизация доказательств, или же эмпирический байесовский.^[12]

Непрерывность

Для гауссовского процесса непрерывность вероятности эквивалентно среднеквадратичная непрерывность,^[13]:145и непрерывность с вероятностью один эквивалентно непрерывность образца.^{[14]:91 «Гауссовские процессы разрывны в фиксированных точках».}Последнее предполагает, но не подразумевается, непрерывность вероятности. Непрерывность вероятности имеет место тогда и только тогда, когда среднее и автоковариантность являются непрерывными функциями. Напротив, непрерывность выборки была сложной задачей даже для стационарные гауссовские процессы (как, вероятно, первым заметил Андрей Колмогоров ), и сложнее для более общих процессов.^{[15]:Разд. 2,8[16]:69,81[17]:80[18]}Как обычно, под непрерывным процессом пробы понимается процесс, который допускает непрерывный образец модификация.^{[19]:292[20]:424}

Стационарный корпус

Для стационарного гауссовского процесса ${ displaystyle X = (X_ {t}) _ {t in mathbb {R}},}$ некоторые условия на его спектр достаточны для непрерывности образца, но не являются необходимыми. Необходимое и достаточное условие, иногда называемое теоремой Дадли-Фернике, включает функцию ${ displaystyle sigma}$ определяется

${ displaystyle sigma (h) = { sqrt { mathbb {E} { big (} X (t + h) -X (t) { big)} ^ {2}}}}$

(правая часть не зависит от ${ displaystyle t}$ из-за стационарности). Непрерывность ${ displaystyle X}$ по вероятности эквивалентна непрерывности ${ displaystyle sigma}$ в ${ displaystyle 0.}$ При сближении ${ displaystyle sigma (h)}$ к ${ displaystyle 0}$ (в качестве ${ displaystyle h to 0}$) слишком медленно, непрерывность образца ${ displaystyle X}$ может потерпеть неудачу. Имеет значение сходимость следующих интегралов:

${ displaystyle I ( sigma) = int _ {0} ^ {1} { frac { sigma (h)} {h { sqrt { log (1 / h)}}}} , dh = int _ {0} ^ { infty} 2 sigma ( mathbb {e} ^ {- x ^ {2}}) , dx,}$

эти два интеграла равны согласно интеграция путем замены ${ displaystyle h = mathbb {e} ^ {- x ^ {2}},}$ ${ displaystyle textstyle x = { sqrt { log (1 / h)}}.}$ Первое подынтегральное выражение не нужно ограничивать как ${ displaystyle h to 0+,}$ таким образом, интеграл может сходиться (${ Displaystyle I ( сигма) < infty}$) или расходятся (${ Displaystyle I ( sigma) = infty}$). Взяв, например, ${ displaystyle sigma ( mathbb {e} ^ {- x ^ {2}}) = { tfrac {1} {x ^ {a}}}}$ для больших ${ displaystyle x,}$ то есть, ${ Displaystyle сигма (ч) = ( журнал (1 / ч)) ^ {- а / 2}}$ для маленьких ${ displaystyle h,}$ можно получить ${ Displaystyle I ( сигма) < infty}$ когда ${ displaystyle a> 1,}$ и ${ Displaystyle I ( sigma) = infty}$ когда ${ Displaystyle 0 <а leq 1.}$В этих двух случаях функция ${ displaystyle sigma}$ увеличивается на ${ displaystyle [0, infty),}$ но обычно это не так. Кроме того, условие

${ displaystyle (*)}$ Существует ${ displaystyle varepsilon> 0}$ такой, что ${ displaystyle sigma}$ монотонно на ${ displaystyle [0, varepsilon]}$

не следует из преемственности ${ displaystyle sigma}$ и очевидные отношения ${ Displaystyle сигма (ч) geq 0}$ (для всех ${ displaystyle h}$) и ${ Displaystyle sigma (0) = 0.}$

Теорема 1. Позволять ${ displaystyle sigma}$ быть непрерывным и удовлетворять ${ displaystyle (*).}$ Тогда условие ${ Displaystyle I ( сигма) < infty}$ необходимо и достаточно для непрерывности образца ${ displaystyle X.}$

Немного истории.^[20]:424Достаточность объявлена Ксавье Ферник в 1964 г., но первое доказательство было опубликовано Ричард М. Дадли в 1967 г.^{[19]:Теорема 7.1.}Необходимость была доказана Майклом Б. Маркусом и Лоуренс Шепп в 1970 г.^[21]:380

Существуют образцы непрерывных процессов ${ displaystyle X}$ такой, что ${ Displaystyle I ( sigma) = infty;}$ они нарушают условие ${ displaystyle (*).}$ Пример, найденный Маркусом и Шеппом ^[21]:387 случайный лакунарный ряд Фурье

${ displaystyle X_ {t} = sum _ {n = 1} ^ { infty} c_ {n} ( xi _ {n} cos lambda _ {n} t + eta _ {n} sin лямбда _ {п} т),}$

куда ${ displaystyle xi _ {1}, eta _ {1}, xi _ {2}, eta _ {2}, dots}$ независимые случайные величины с стандартное нормальное распределение; частоты ${ displaystyle 0 < lambda _ {1} < lambda _ {2} < dots}$ являются быстрорастущей последовательностью; и коэффициенты ${ displaystyle c_ {n}> 0}$ удовлетворить ${ displaystyle textstyle sum _ {n} c_ {n} < infty.}$ Последнее соотношение подразумевает ${ displaystyle textstyle mathbb {E} sum _ {n} c_ {n} (| xi _ {n} | + | eta _ {n} |) = sum _ {n} c_ {n} mathbb {E} (| xi _ {n} | + | eta _ {n} |) = { text {const}} cdot sum _ {n} c_ {n} < infty,}$ откуда ${ displaystyle sum _ {n} c_ {n} (| xi _ {n} | + | eta _ {n} |) < infty}$ почти наверняка, что обеспечивает равномерную сходимость ряда Фурье почти наверняка, а выборочную непрерывность ${ displaystyle X.}$

Автокорреляция случайного лакунарного ряда Фурье

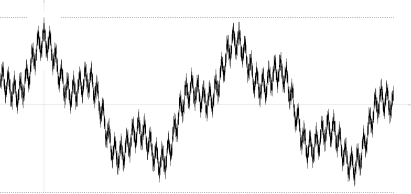
Его автоковариационная функция

${ displaystyle mathbb {E} X_ {t} X_ {t + h} = sum _ {n = 1} ^ { infty} c_ {n} ^ {2} cos lambda _ {n} h}$

нигде не монотонна (см. рисунок), как и соответствующая функция ${ displaystyle sigma,}$

${ displaystyle sigma (h) = { sqrt {2 mathbb {E} X_ {t} X_ {t} -2 mathbb {E} X_ {t} X_ {t + h}}} = 2 { sqrt { sum _ {n = 1} ^ { infty} c_ {n} ^ {2} sin ^ {2} { frac { lambda _ {n} h} {2}}}}.}.}$

Броуновское движение как интеграл гауссовских процессов

А Винеровский процесс (он же броуновское движение) является интегралом обобщенный гауссовский процесс белого шума. Это не так стационарный, но имеет стационарные приращения.

В Процесс Орнштейна – Уленбека это стационарный Гауссовский процесс.

В Броуновский мост является (как и процесс Орнштейна – Уленбека) примером гауссовского процесса, приращения которого не являются независимый.

В дробное броуновское движение является гауссовским процессом, ковариационная функция которого является обобщением ковариационной функции винеровского процесса.

Закон нуля или единицы Дрисколла

Закон нуля или единицы Дрисколла - это результат, характеризующий выборочные функции, генерируемые гауссовским процессом.

Позволять ${ displaystyle f}$ - гауссовский процесс с нулевым средним ${ displaystyle left {X_ {t}; т in T right }}$ с неотрицательно определенной ковариационной функцией ${ displaystyle K}$. Позволять ${ Displaystyle { mathcal {H}} (R)}$ быть Воспроизведение ядра гильбертова пространства с положительно определенным ядром ${ displaystyle R}$.

потом

${ displaystyle lim _ {n to infty} operatorname {tr} [K_ {n} R_ {n} ^ {- 1}] < infty}$,

куда ${ displaystyle K_ {n}}$ и ${ displaystyle R_ {n}}$ ковариационные матрицы всех возможных пар ${ displaystyle n}$ очков, подразумевает

${ Displaystyle Pr [е в { mathcal {H}} (R)] = 1}$.

Более того,

${ displaystyle lim _ {n to infty} operatorname {tr} [K_ {n} R_ {n} ^ {- 1}] = infty}$

подразумевает

${ Displaystyle Pr [е в { mathcal {H}} (R)] = 0}$.^[22]

Это имеет серьезные последствия, когда ${ displaystyle K = R}$, так как

${ displaystyle lim _ {n to infty} operatorname {tr} [R_ {n} R_ {n} ^ {- 1}] = lim _ {n to infty} operatorname {tr} [ I] = lim _ {n to infty} n = infty}$.

Таким образом, почти все выборочные пути гауссовского процесса с нулевым средним и положительно определенным ядром ${ displaystyle K}$ будет лежать вне гильбертова пространства ${ Displaystyle { mathcal {H}} (К)}$.

Гауссовские процессы с линейными ограничениями

Для многих интересных приложений уже даны некоторые ранее существовавшие знания о системе. Рассмотрим, например, случай, когда выход гауссова процесса соответствует магнитному полю; здесь реальное магнитное поле ограничено уравнениями Максвелла, и было бы желательно включить это ограничение в формализм гауссовского процесса, поскольку это, вероятно, улучшило бы точность алгоритма.

Метод включения линейных ограничений в гауссовские процессы уже существует:^[23]

Рассмотрим (векторную) выходную функцию ${ displaystyle f (x)}$ который, как известно, подчиняется линейному ограничению (т.е. ${ displaystyle { mathcal {F}} _ {X}}$ является линейным оператором)

${ displaystyle { mathcal {F}} _ {X} (f (x)) = 0.}$

Тогда ограничение ${ displaystyle { mathcal {F}} _ {X}}$ можно выполнить, выбрав ${ Displaystyle е (х) = { mathcal {G}} _ {X} (г (х))}$, куда ${ Displaystyle г (х) sim { mathcal {GP}} ( mu _ {g}, K_ {g})}$ моделируется как гауссовский процесс, и нахождение ${ Displaystyle { mathcal {G}} _ {X}}$ s.t.

${ displaystyle { mathcal {F}} _ {X} ({ mathcal {G}} _ {X} (g)) = 0 qquad forall g.}$

Данный ${ displaystyle { mathcal {G}} _ {X}}$ и используя тот факт, что гауссовские процессы замкнуты относительно линейных преобразований, гауссовский процесс для ${ displaystyle f}$ подчиняться принуждению ${ displaystyle { mathcal {F}} _ {X}}$ становится

${ displaystyle f (x) = { mathcal {G}} _ {X} g sim { mathcal {GP}} ({ mathcal {G}} _ {X} mu _ {g}, { mathcal {G}} _ {X} K_ {g} { mathcal {G}} _ {X '} ^ {T}).}$

Следовательно, линейные ограничения могут быть закодированы в среднее значение и ковариационную функцию гауссовского процесса.

Приложения

Пример регрессии (прогнозирования) гауссовского процесса по сравнению с другими моделями регрессии.^[24]

Гауссовский процесс можно использовать как априорное распределение вероятностей над функции в Байесовский вывод.^[10][25] Учитывая любой набор N точек в желаемой области ваших функций, возьмите многомерный гауссовский чья ковариация матрица параметр - это Матрица Грама вашей N точки с некоторыми желательными ядро, и образец от этого гауссовского. Для решения задачи прогнозирования с несколькими выходами была разработана регрессия гауссовского процесса для векторнозначной функции. В этом методе строится «большая» ковариация, которая описывает корреляции между всеми входными и выходными переменными, взятыми в N точки в желаемом домене.^[26] Этот подход был подробно разработан для матричнозначных гауссовских процессов и обобщен на процессы с «более тяжелыми хвостами», такими как Студенческие процессы.^[3]

Вывод непрерывных значений с помощью предшествующего гауссовского процесса известен как регрессия гауссовского процесса, или кригинг; расширение регрессии гауссовского процесса до несколько целевых переменных известен как кокригинг.^[27] Таким образом, гауссовские процессы полезны как мощная нелинейная многомерная интерполяция инструмент. Гауссовская регрессия процесса может быть расширена для решения задач обучения как в под наблюдением (например, вероятностная классификация^[10]) и без присмотра (например. многообразное обучение^[8]) учебные рамки.

Гауссовские процессы также могут использоваться, например, в контексте смешанных моделей экспертов.^[28][29] Основное обоснование такой структуры обучения состоит в предположении, что данное отображение не может быть хорошо охвачено одной гауссовой моделью процесса. Вместо этого пространство наблюдения разделено на подмножества, каждое из которых характеризуется различной функцией отображения; каждый из них изучается через разные компоненты гауссовского процесса в постулируемой смеси.

Прогнозирование гауссовского процесса или кригинг

Гауссовский процесс регрессии (прогноз) с квадратом экспоненциального ядра. Левый график взят из предыдущего распределения функций. Середина - это рисунки сзади. Справа - средний прогноз с заштрихованным одним стандартным отклонением.

При рассмотрении общей задачи регрессии гауссовского процесса (кригинга) предполагается, что для гауссовского процесса ${ displaystyle f}$ наблюдается в координатах ${ displaystyle x}$, вектор значений ${ displaystyle f (x)}$ это всего лишь один образец из многомерного гауссовского распределения размерности, равной количеству наблюдаемых координат ${ displaystyle n}$. Следовательно, в предположении распределения с нулевым средним ${ Displaystyle е (х) сим N (0, К ( тета, х, х '))}$, куда ${ Displaystyle К ( тета, х, х ')}$ ковариационная матрица между всеми возможными парами ${ Displaystyle (х, х ')}$ для заданного набора гиперпараметров θ.^[10]Таким образом, маргинальная вероятность журнала составляет:

${ Displaystyle журнал п (е (х) середина тета, х) = - { гидроразрыва {1} {2}} е (х) ^ {Т} К ( тета, х, х ') ^ { -1} f (x ') - { frac {1} {2}} log det (K ( theta, x, x')) - { frac {n} {2}} log 2 число Пи }$

и максимизируя эту предельную вероятность θ обеспечивает полную спецификацию гауссовского процесса ж. Здесь можно вкратце отметить, что первый член соответствует штрафному члену за неспособность модели соответствовать наблюдаемым значениям, а второй член - штрафному члену, который увеличивается пропорционально сложности модели. Указав θ делать прогнозы о ненаблюдаемых ценностях ${ Displaystyle f (х ^ {*})}$ в координатах Икс* в таком случае нужно всего лишь взять образцы из прогнозного распределения. ${ displaystyle p (y ^ {*} mid x ^ {*}, f (x), x) = N (y ^ {*} mid A, B)}$ где апостериорная средняя оценка А определяется как

${ Displaystyle А = К ( тета, х ^ {*}, х) К ( тета, х, х ') ^ {- 1} е (х)}$

и оценка апостериорной дисперсии B определяется как:

${ displaystyle B = K ( theta, x ^ {*}, x ^ {*}) - K ( theta, x ^ {*}, x) K ( theta, x, x ') ^ {- 1 } К ( theta, x ^ {*}, x) ^ {T}}$

куда ${ Displaystyle К ( тета, х ^ {*}, х)}$ ковариация между новой координатой оценки Икс* и все другие наблюдаемые координаты Икс для данного вектора гиперпараметров θ, ${ Displaystyle К ( тета, х, х ')}$ и ${ displaystyle f (x)}$ определены как раньше и ${ Displaystyle К ( тета, х ^ {*}, х ^ {*})}$ дисперсия в точке Икс* как продиктовано θ. Важно отметить, что практически апостериорная средняя оценка ${ Displaystyle f (х ^ {*})}$ («точечная оценка») - это просто линейная комбинация наблюдений ${ displaystyle f (x)}$; аналогичным образом дисперсия ${ Displaystyle f (х ^ {*})}$ фактически не зависит от наблюдений ${ displaystyle f (x)}$. Известным узким местом в прогнозировании гауссовского процесса является то, что вычислительная сложность вывода и оценки правдоподобия является кубической по количеству точек |Икс|, и поэтому может стать невозможным для больших наборов данных.^[9] Работает над разреженными гауссовскими процессами, которые обычно основаны на идее построения представительный набор для данного процесса ж, попробуйте обойти эту проблему.^[30][31]

Байесовские нейронные сети как гауссовские процессы

Байесовские нейронные сети - это особый тип Байесовская сеть что является результатом лечения глубокое обучение и искусственная нейронная сеть моделирует вероятностно, и присваивая предварительное распространение к их параметры. Вычисления в искусственных нейронных сетях обычно организованы в последовательные слои искусственные нейроны. Количество нейронов в слое называется шириной слоя. По мере увеличения ширины слоя многие байесовские нейронные сети сводятся к гауссовскому процессу с закрытая форма композиционное ядро. Этот гауссовский процесс называется гауссовским процессом нейронной сети (NNGP). Он позволяет более эффективно оценивать прогнозы байесовских нейронных сетей и предоставляет аналитический инструмент для понимания глубокое обучение модели.

Вычислительные проблемы

В практических приложениях модели гауссовских процессов часто оцениваются на сетке, приводящей к многомерным нормальным распределениям. Использование этих моделей для прогнозирования или оценки параметров с использованием максимального правдоподобия требует оценки многомерной гауссовой плотности, которая включает в себя вычисление детерминанта и обратного значения ковариационной матрицы. Обе эти операции имеют кубическую вычислительную сложность, а это означает, что даже для сеток небольшого размера обе операции могут иметь непомерно высокие вычислительные затраты. Этот недостаток привел к развитию множества методы аппроксимации.

Смотрите также

• Линейная статистика Байеса
• Байесовская интерпретация регуляризации
• Кригинг
• Гауссово свободное поле
• Процесс Гаусса – Маркова
• Кригинг с усилением градиента (GEK)
• Студенческий t-процесс

Рекомендации

внешняя ссылка

• Веб-сайт гауссовских процессов, включая текст гауссовских процессов для машинного обучения Расмуссена и Вильямса
• Мягкое введение в гауссовские процессы
• Обзор гауссовских случайных полей и корреляционных функций
• Эффективное обучение с подкреплением с использованием гауссовских процессов

Программного обеспечения

• GPML: комплексный набор инструментов Matlab для регрессии и классификации GP
• STK: небольшой (Matlab / Octave) набор инструментов для кригинга и моделирования GP
• Модуль кригинга в фреймворке UQLab (Matlab)
• Функция Matlab / Octave для стационарных гауссовских полей
• Yelp MOE - механизм оптимизации черного ящика с использованием процесса обучения по Гауссу
• ooDACE - Гибкий объектно-ориентированный набор инструментов Kriging Matlab.
• GPstuff - набор инструментов гауссовского процесса для Matlab и Octave
• GPy - фреймворк гауссовских процессов на Python
• GSTools - набор инструментов для геостатистики, включая регрессию гауссовского процесса, написанный на Python.
• Интерактивная демонстрация регрессии гауссовского процесса
• Базовая библиотека процессов Гаусса, написанная на C ++ 11
• scikit-learn - Библиотека машинного обучения для Python, которая включает регрессию и классификацию гауссовских процессов.
• [1] - Набор инструментов Kriging (KriKit) разработан в Институте био- и геонаук 1 (IBG-1) Forschungszentrum Jülich (FZJ)

Видео уроки

• Основы гауссовского процесса Дэвида Маккея
• Обучение с помощью гауссовских процессов Карла Эдварда Расмуссена
• Байесовский вывод и гауссовские процессы Карла Эдварда Расмуссена